水文频率计算中窗宽和核函数对密度函数估计影响分析

董 洁，刁艳芳，谭秀翠，徐 妍

(山东农业大学水利土木工程学院，山东 泰安 271018)

水利建设规划设计时，要确定一个合理的设计标准或工程规模。一般采用水文频率计算方法计算设计值，目前主要有参数和非参数数理统计方法[1]。水文频率计算需要对水文变量的总体密度进行估计。如果密度函数结构已知而只有其中某些参数未知，此时的密度估计就是传统的参数估计问题。如果密度函数未知(或最多只知道连续、可微等条件)，仅从即有的样本出发得出密度函数的表达式，这就是非参数密度估计。非参数密度估计始于直方图法，后来发展为最近邻法、核估计法等，其中理论发展最完善的是密度的核估计法[2]。

1 核估计

1.1 概 述

设{x1,…,xn}为离散的随机样本，单变量核密度估计为：

(1)

核估计既与样本有关，又与核及窗宽的选取有关。在给定样本以后，一个核估计的好坏，取决于核及窗宽的选取是否得当。窗宽和核的选择直接影响密度函数的估计精度[3]。

(2)

1.2 最优窗宽的确定

1.2.1 理论界定

(3)

从而可以得到这种意义下的最优窗宽表达式：

(4)

由此可以看出：

(1)最优窗宽应随样本的增大而不断减小且速度为o(n)。

(2)f″(x)反映密度函数的震动速率，剧烈震动的密度函数应对应较小的最优窗宽。

(3)表达式中含有未知量f″(x)，因此无法得到具体的窗宽数值。

1.2.2 窗宽的选择

窗宽的选择一般分为固定和变窗宽[4,5]。

(1)固定窗宽。就是在每一个拟合点取等窗宽，缺点是所估计量不能充分利用变量X的设计密度所提供的信息，且对复杂曲线的拟合效果欠佳。

(2)变窗宽。有局部变窗宽和全局变窗宽2类。局部变窗宽h(x0)随位置x0的变化而变化，全局变窗宽h(xj)随数据点xj的变化而变化。变窗宽的引入可以反映不同点的光滑程度，降低拟合曲线在峰顶区域的偏差以及尾部区域的方差，提高拟合曲线的灵活性，适用于空间非齐次曲线的拟合。例如交叉证实法Cross-Validation(CV)。

前面提到的窗宽选择需要对拟合的密度函数有一定的假设，而CV法是一种数据本源(data based)方法，不需要对拟合密度函数假设，而是从现有的数据直接得到合理的窗宽。由样本{X1,X2,…,Xn}作缺值估计：

(5)

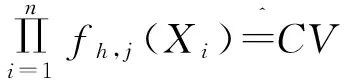
但是，当核不是密度函数时，估计量已经不是密度函数，进而不能用极大似然的思想求得，我们可以由以下最小平方差的思想LSCV(Least Square CV)求之，算出积分平方差ISE(Integrated Square Error):

(6)

好的密度估计函数应对应较小的ISE，或:

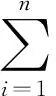
(7)

(8)

可以得到“最优”窗宽。但是在实践中常会出现不够光滑的现象，而且这种窗宽的计算量太大，占用的时间太长，因而，下面给出简便可行的方法。

1.2.3 确定最优窗宽的具体方法

表1 拟合不同密度函数时窗宽的计算结果Tab.1 The window width calculation results of fittingdifferent density function

1.3 核的选择

(1)一般核函数属于对称的密度函数族P，即q(·)满足如下条件：

(9)

从减小积分均方误差(L2)的角度来看，Silverman[6]指出P族中不同核对减小积分均方误差没有明显差别，因此一般可根据其他需要(如计算方便)选定合适的核。后面的实例中就是考虑到计算方便以及水文的特点，我们选用了指数函数作为核。

(2)核函数为高阶函数族Hs，即其中q(·)满足如下条件：

(12)

引入这种函数的道理是基于以下命题。

命题：设核q(·)∈Hs具有s阶导数，则积分均方误差为：

(13)

从命题可以看出这种核的优势在于随着阶s的增大：

(14)

随之减小，进而积分均方差减小，不足是由它做成的核不是非负函数，进而不是密度函数。因此，在水文计算中，我们通常不选此类核。

2 模拟研究

2.1 窗宽对模拟结果的影响

为了考证不同窗宽对密度拟合的影响，以下模拟以对数正态密度曲线为所要估计的曲线，以指数核(2)为核函数，分别取4种依次递增窗宽(1，2，3，4)进行了模拟。从图1～图4中可以看出，随着窗宽的增大，模拟曲线也越光滑，所以窗宽的选择对估计结果有较大的影响。

2.2 核对估计误差的影响

前面已经指出，不同核的估计量的影响在实践中不大，为验证它，我们用计算机随机生成500个服从对数正态分布的随机数，分别以不同的核作为密度估计量，为了便于比较，取同样的窗宽，并做其图形，考察这些模拟图形对理论对数正态密度函数的拟合情况。在模拟中分别取以下核。

(1)均匀核：

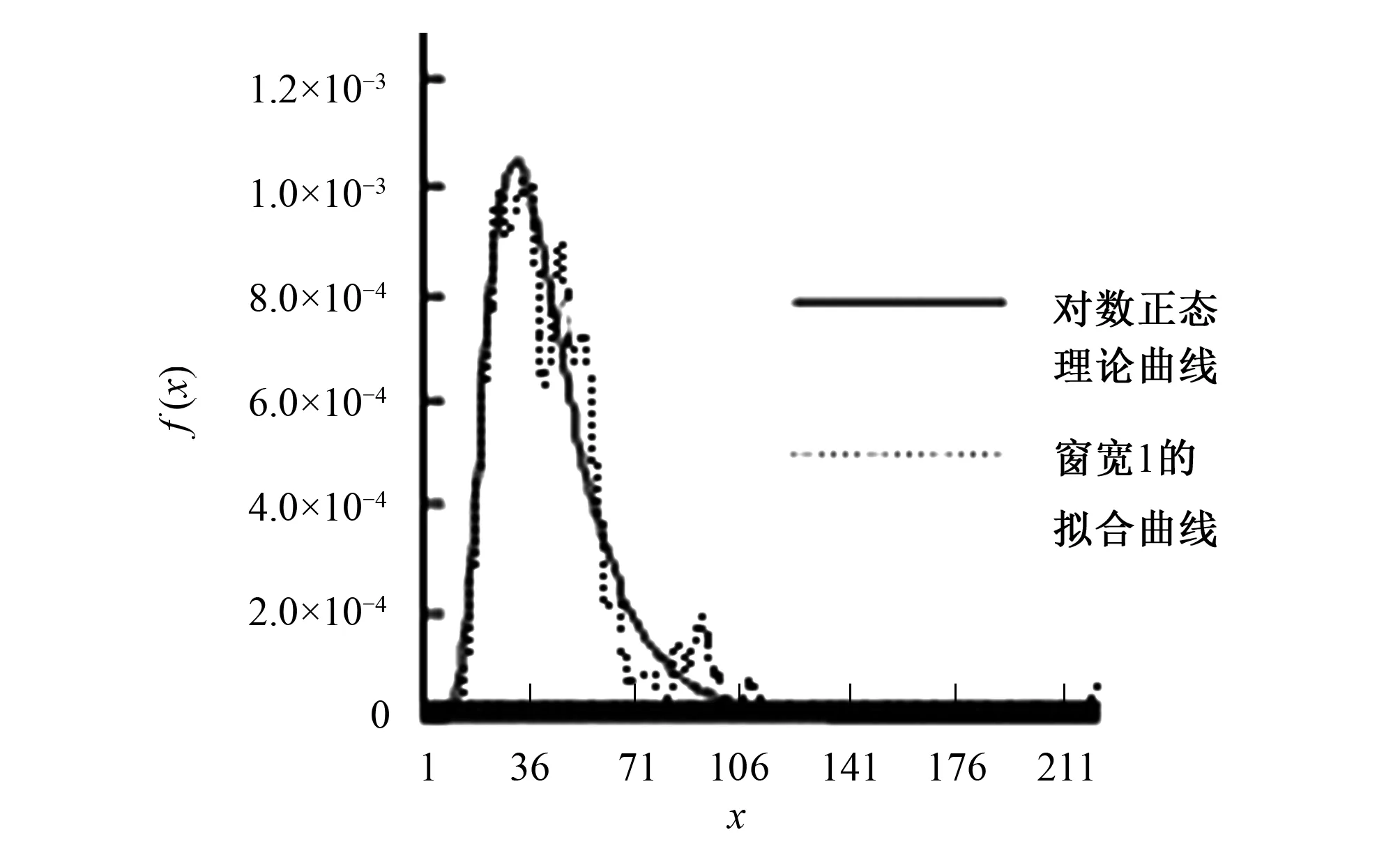
图1 窗宽1拟合曲线Fig.1 Window width 1 fitting curve

图2 窗宽2拟合曲线Fig.2 Window width 2 fitting curve

图3 窗宽3拟合曲线Fig.3 Window width3 fitting curve

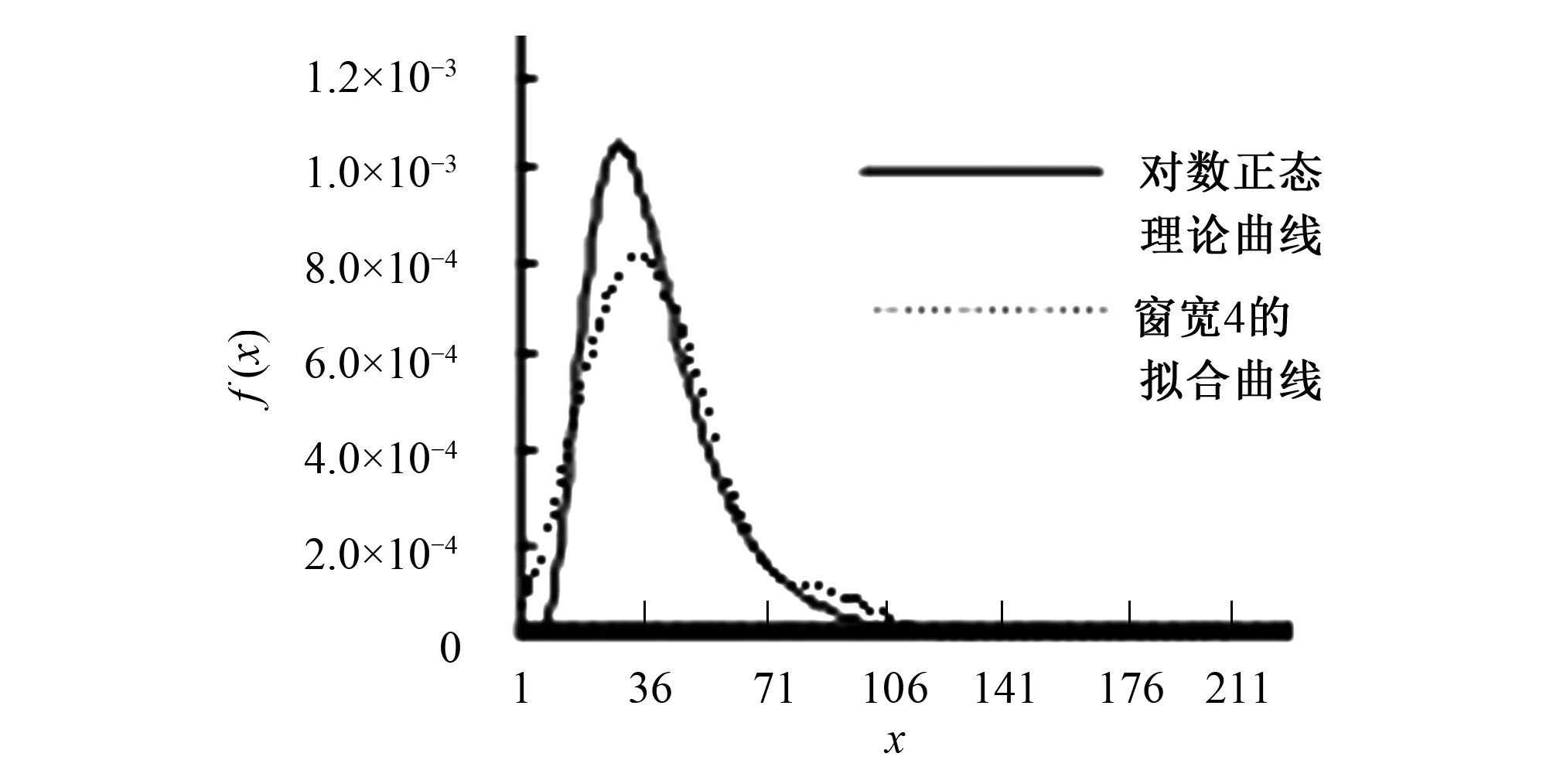
图4 窗宽4拟合曲线Fig.4 Window width 4 fitting curve

(2)指数核:

(3)cauchy核：

(4)EV1核：

q(x)=exp [-x2-exp(-x2)]

图5～图8中光滑曲线是对数正态密度曲线，其余曲线是分别以上述核为函数的模拟曲线。

从模拟的结果可以看出，均匀核模拟曲线不够光滑，指数核最好，其他核比较光滑，差别也不太多。

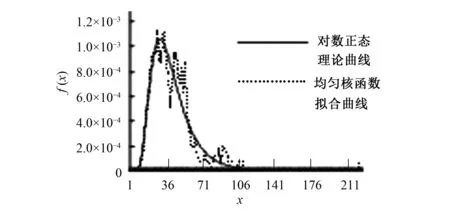
图5 均匀核拟合曲线Fig.5 Uniform kernel fitting curve

图6 指数核拟合曲线Fig.6 Exponential kernel fitting curve

图7 cauchy核拟合曲线Fig.7 Cauchy kernel fitting curve

图8 EV1核拟合曲线Fig.8 EV1 nuclear fitting curve

3 水文频率计算模型实例

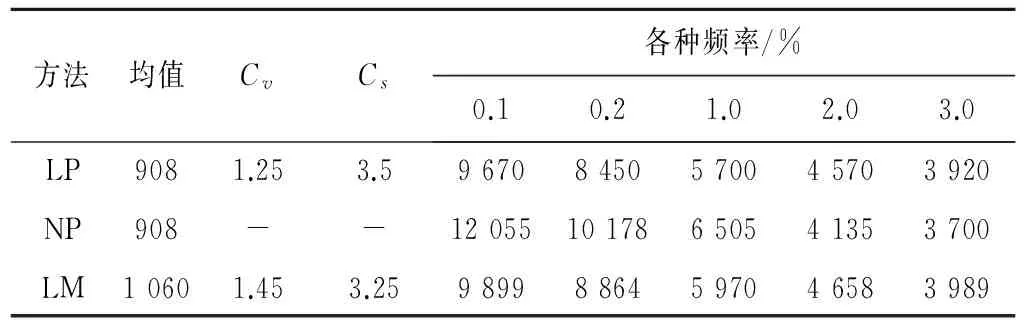
表2 五龙口水文站径流量频率计算Tab.2 runoff frequency calculation of Wulongkou station

经过用参数适线法(LP)、线性距法(LM)和非参数核估计方法(NP)分析论证，频率小于1%时，非参数核估计法计算的流量设计值要大于参数法，频率大于1%时，非参数核估计法的流量设计值要小于参数法。3种方法结合使用，可以对比分析，以确定较合理的流量设计值。

4 结 语

(1)分析了核估计方法中的核和窗宽的选择问题，并针对不同的核、窗宽对估计结果产生的影响进行了模拟研究。结果表明，指数核的拟合较好；窗宽的选取是非常重要的，它决定着拟合的计精度。最优窗宽应当使统计量的积分均方差(MISE)最小，并推出了最优窗宽的近似计算公式。

(2)根据核函数和最优窗宽的讨论，用非参数核估计和参数适线法、线性距法对五龙口水文站的流量进行了频率计算，通过3种方法对比分析，可以确定合理的流量设计值，为解决水文频率计算提供了有效方法。

□

[1] 黄振平，陈元芳.水文统计学[M].北京：中国水利水电出版社，2011.

[2] 陈希儒，柴根象.非参数统计教程[M].上海：华东师范大学出版社，1993.

[3] C G Lambert. Efficient on-line nonparametric kernel density estimation[J]. Algorithmica, 2004,25(1).

[4] Adamowski k. Regional analysis of analysis of annual maximum and partial duration flood data by nonparametric and l-moment methods[J].Journal of Hydrology，2000，(229)：219-231.

[5] Goel N K. A derived flood frequency distribution for correlated rainfall intensity and duration[J].Journal of Hydrology 2000,(228):56-67.

[6] Silverman B W. Choosing window width when estimating a density[J]. Biometrika，1978,(65):1-11.

[7] 闫宝伟，刘彦成. 基于两变量核密度估计的枯水频率分析[J]. 人民珠江,2017,38(4):15-20.

[8] 王雪妮，周 晶.一种新的洪水频率分析方法研究[J].水利学报，2016,47(6):798-802.