考虑空间变异性的桩基础可靠度设计方法比较研究

张飞龙，曹子君

（1苏交科集团股份有限公司，江苏 南京 211112；2武汉大学水利水电学院，湖北 武汉430072）

岩土材料是天然的材料，受其形成过程中各种地质作用的影响其材料特性存在很大的变异性。岩土材料的固有空间变异性（Inherent spatial variability,ISV）是岩土工程中不确定性的一个主要来源［1］，通常，在岩土工程可靠度设计（Reliability-based design,RBD）中利用等效方差折减法（Equivalent variance technique，EVT）间接、近似地考虑材料的固有空间变异性。目前，系统的表征这种间接、近似的考虑固有空间变异性的方法对岩土结构可靠度设计结果影响的研究并不多见。近年来针对岩土工程桩基础设计，Wang和Cao提出了一种基于蒙特卡洛模拟（Monte Carlo simulation，MCS）的可靠度设计方法，即扩展可靠度设计方法（Expanded RBD［3-5］）。该方法可以采用不同的表征固有空间变异性模型来灵活地考虑岩土工程可靠度设计中模型的不确定性，例如：基于随机场模型（Random field model，RFM）［2］的显式模型和基于等效方差折减法的隐式模型。利用扩展可靠度设计方法的上述优势，对钻孔桩案例进行设计分析，分别采用随机场法和等效方差折减法模拟岩土材料参数的固有空间变异性，将两种方法的设计结果进行对比，研究间接模拟参数空间变异性时对钻孔桩可靠度设计结果的影响。文章首先介绍了在钻孔桩可靠度设计中利用RFM和EVT考虑岩土体参数固有空间变异性的概率模型；然后以钻孔桩设计为例，将两种不同模型对设计结果的影响做了对比分析。

1 岩土体参数固有空间变异性的概率模型

1.1 基于RFM的显式概率模型

考虑如图1所示的钻孔桩布置在均质土中，有效应力摩擦角φ'沿土层深度方向的空间变异性用竖向一维随机场φ'（z）进行表征。其中，z为土层深度；φ'服从均值为μφ'，标准差为σφ'（或变异系数COVφ'=σφ'/μφ'）的对数正态分布。φ'（z）由一系列随机变量φ'组成，代表不同深度处土层的有效应力摩擦角。随机场理论中，任意不同位置的φ'之间的空间相关性可由波动范围λ和相关函数ρ（比如单一指数型相关函数）进行表示［2］，对给定的相关函数，可以使用Cholesky分解对随机场进行离散和模拟处理，钻孔桩可靠度设计中随机场离散和模拟的详细步骤可参考文献［5］。虽然随机场模型可以显式地描述空间变异性，但是目前研究相对有限，在岩土结构可靠度设计中，通常应用随机场模型模拟岩土性质的空间变异性。当前的可靠度设计方法中，通常用等效方差折减法以隐式的方式表征空间变异性。

图1 固有空间变异性模型示意图

1.2 基于EVT的隐式概率模型

在等效方差折减法中，一定范围内均质土的土体特性（如深度范围为Δz的均质土）可由一个随机变量表示，该随机变量代表了相应范围内的土体特性在空间上的局部平均效应，并且由于这种空间平均效应的存在，使得该随机变量的方差存在一定的折减［2］。以图1所示布置在均质土中的钻孔桩为例，考虑φ'服从对数正态分布的情形（与上节一致），假设φ'Δz代表沿深度为Δz土层内φ'的空间平均值，由于空间平均效应的存在，等效正态随机变量lnφ'的方差存在一定的折减，lnφ'的方差折减程度可由方差折减系数表示。例如，单一指数型相关结构的可由式（1）计算［2］：

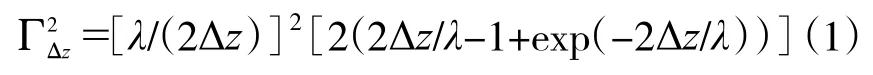
在岩土工程相关文献中， 通常可近似的由式（2）计算：

式（1）和式（2）分别为方差折减函数的精确和简化计算形式。对于钻孔桩设计问题，其总抗力由侧向抗力Qside和底部抗力Qtip两部分组成，图1中显示了Qside和Qtip的影响区域。Qside的影响区域为沿钻孔桩深度D的部分，因此Qside的影响区域长度为D；Qtip的影响区域为桩底部以上La与桩底部以下Lb之间的部分，因此Qtip的影响区域长度L为La和Lb的和，即L=La+Lb。计算Qside和Qtip需要各自影响区域（D和L）的φ'值，假设φ'side和φ'tip分别代表沿深度区间D和L进行空间平均的φ'值，可靠度设计过程中它们对应的随机样本可通过方差折减函数计算，应用EVT产生φ'side和φ'tip随机样本的详细过程可参考文献［5］。

值得注意的是，RFM和EVT都可以方便地应用于岩土结构扩展可靠度设计中来模拟岩土体参数的固有空间变异性。在扩展可靠度设计中，钻孔桩的设计问题通常被看作扩展可靠性问题，通常将设计参数（如直径B和桩长D）作为独立的离散随机变量考虑，然后设计过程可以转变为计算B和D各种设计组合情况下的失效概率P（Failure|B，D）的过程，最终确定满足P（Failure|B，D）≤目标失效概率PT的可行设计。

2 不同空间变异性模拟方法对桩基础可靠度设计的影响

Wang和Cao［5］利用图2所示的钻孔桩设计案例说明了扩展可靠度的方法。钻孔桩置于松砂中，砂体的重度γ=20 kN/m3，有效内摩擦角平均值μφ'=32°和变异系数为COVφ'=17%，平均水平土压力系数μK0=1.0，桩径B=1.2 m，材料为混凝土，容重γcon=24.0 kN/m3，原位水平应力系数率（K/K0）n=1.0，地下水位处于地表。假设该钻孔桩的极限状态为：在设计载荷为F50=800 kN，排水条件下，桩体的允许位移ya=25 mm。在钻孔桩设计中，桩径B和桩长D作为关键设计参数在承载轴向荷载和抵抗桩体位移方面起着至关重要的作用。Wang和Cao［5］利用扩展可靠度设计方法结合RFM（单一指数型相关结构）研究φ'的固有空间变异性对设计结果的影响，研究表明：在给定B的情况下，φ'的固有空间变异性显著影响着D的最小可行设计值（Dmin）。图3中的三角形符号代表了在B=1.2m情况下Dmin随波动范围λ的变化情况，其中Dmin值是正常使用极限状态下，根据目标失效概率PT=0.004 7确定。如图3所示，当λ从0.2 m增加至+∞时（空间相关性增大），Dmin从3.2 m增加至8.0 m。该钻孔桩设计实例详细的建模和计算过程可参考文献［5］。

图2 钻孔桩设计案例示意图［4］

为了进行对比，利用扩展可靠度设计法结合EVT对钻孔桩进行重新设计，其中EVT中的方差折减系数由其精确计算形式（式（1））或者简化计算形式（式（2））得到。应用扩展可靠度设计方法可得到每个λ对应的两个Dmin（分别对应方差折减函数的两种形式）。图3中圆形和十字形符号分别表示在B=1.2m情况下Dmin随归一化的波动范围λ/Lmax的变化情况，其中Lmax为影响区的最大长度，本算例取为8B+3.5B=13.8 m。图3中圆形代表了使用精确方差折减函数时的计算结果，十字形代表了使用简化方差折减函数时的计算结果。为了完整的研究λ的影响规律，本文λ的取值范围为0.2 m~+∞，但是需要指出的是当λ大于桩身长度和影响区的最大长度后（即λ/Lmax＞1），将不再对可靠度设计结果产生显著影响。

图3 隐式模型对可行设计的影响

如图3所示，对于给定的λ值，使用方差折减函数精确形式的EVT法得出的设计结果与使用RFM得出的设计结果基本一致。图3还表明，当λ＜1m或λ＞100 m时使用方差折减函数简化形式的EVT法得出的设计结果与使用RFM得出的设计结果基本一致；另一方面，当1 m＜λ＜100 m时，使用方差折减函数简化形式的EVT法将导致相对保守的设计结果。由于该范围涵盖了土体特性在竖直方向上的典型波动范围［1］，因此，在实际钻孔桩设计过程中，使用方差折减函数简化形式的EVT法将导致较为保守的设计结果。

3 结论

使用RFM和EVT对钻孔桩设计中岩土体参数的空间变异性进行模拟，并对设计结果进行了对比分析。利用扩展可靠的设计方法对钻孔桩设计案例进行可靠度设计，对比EVT法模拟固有空间变异性的设计结果和使用RFM法模拟固有空间变异性的设计结果的区别，发现在钻孔桩设计中使用方差折减函数精确形式的EVT法所得的设计结果与使用RFM方法所得到的设计结果一致，而使用方差折减函数简化形式的EVT法所得的设计结果可能导致较为保守的设计结果。

本文研究了单层土中空间变异性对桩基础可靠度设计的影响规律，下一步将基于空间变异性的定量分析进一步探讨成层土中桩基础可靠度设计问题。

［1］Phoon K K，Kulhawy F H. （1999）. Characterization of geotechnical variability［J］. Canadian Geotechnical Journal，36（4）： 612-624.

［2］Vanmarcke E H. Random Fields：Analysis and Synthesis［M］.Cambridge：MIT Press，1983.

［3］Wang Y. Reliability-based design of spread foundations by Monte Carlo simulations［J］. Geotechnique，2011，61（8）：677-685.

［4］Wang Y，Au S K，Kulhawy F H. Expanded reliability-based design approach for drilled shafts［J］. Journal of Geotechnical and Geoenvironmental Engineering，2011，137（2）：140-149.

［5］Wang Y，Cao Z. E xpanded Reliability-based Design of Piles in Spatially Variable Soil Using Efficient Monte Carlo Simulations［J］. Soils and Foundations，2013，53（6）：820-834.