干涉型光纤预警系统入侵信号的调制解调技术

张叶浩,衣文索,崔光磊,王家宁

0 引 言

分布式光纤传感技术集传感和传输于一体,可同时探测物理量的空间分布信息和时变信息,具有抗电磁干扰、体积小和低成本等优势,因而其极适合应用于监测油气管道、输水管道、军事区域和边界国界等大范围实时预警系统中[1-4]。相比于散色型光纤传感系统,基于光纤干涉仪的干涉型系统实时性好、易于实现、无盲区、灵敏度极高,具有很好的实用和经济价值[5,6]。

对入侵信号的精确识别与精准定位是光纤预警系统的两个关键技术[7],入侵行为引起的振动波会导致传感光纤的特征参量的改变进而调制到光纤内的光信号相位中,最终光电探测器将光纤中两束光干涉后的光强转换为电信号后由预警系统高速信号处理单元进行有效分析。然而在工程应用中,由于受到环境随机外力及温度等因素影响,传输光偏振态将产生随机退化,即“偏振诱导衰落”与“偏振诱导相位偏移”现象[8]。这致使调制后的光强信号特征改变引起系统误报,并且由于入侵信号定位技术普遍采用互相关时延估计算法,其定位精度降低取决于信号的相关性[9],而相位偏移现象会显著降低两路信号的相关程度,从而无法满足工程应用需求,制约干涉型光纤传感系统的发展。因此,从干涉信号中解调出被测信号原始相移量是系统工程应用的关键技术之一。根据干涉信号光与参考光频率差是否为0,分为无源零差法、有源零差法和外差法。有源零差法与外差法检测系统复杂,响应带宽差,无法实现全光纤化,因而较少使用。无源零差法包括主动型相位生成载波法与基于耦合器的微分交叉相乘法,反正切法和离散化方法等被动型解调[10,11]。微分交叉相乘法对光源稳定性要求低,实现方法简单,动态响应范围不受载波频率限制[12],更适用于工程应用。

针对上述问题,笔者在分析干涉型光纤预警系统信号调制原理与偏振退化现象的基础上,采用基于3×3耦合器的微分交叉相乘法进行信号解调,并提出“短时峰峰值检测法”调校失真。Simulink仿真结果表明,该方法多种情形下均可高保真还原信号,具有工程指导意义。

1 干涉型光纤预警系统中信号调制原理

1.1 系统结构

以目前工程实用价值最高的基于3×3耦合器的Mach Zehnder干涉系统为例,其等效结构如图1所示。工作过程为:激光二极管发出1 550 nm窄带激光经过单向光学隔离器后由3 dB耦合器C1等功率分成两束光。一束沿顺时针进入光纤环行器R1后,通过3×3耦合器C2等功率分成3束光,分别进入传感光纤臂1、参考光纤臂2与光纤黑盒防止回波干扰,然后光臂中的传感光由3×3耦合器C3合束并产生干涉效应,即该干涉光含有振动信号,再经C3分成3路2/3π有相位差的光强信号分别由光电探测器PB1、PB2与PB3转化为电压信号,最终经过调理和A/D转换后进入上位机分析处理。同理,耦合器C1分出的另一束光沿逆时针进入光纤环行器R2再经过3×3耦合器C3后在耦合器C2处产生干涉,然后进入光电探测器PA1、PA2与PA3,最终同样经过调理后进入上位机分析处理。

图1 基于3×3耦合器的Mach Zehnder干涉系统结构图Fig.1 Mach Zehnder interferometric system structure diagram based on 3×3 coupler

1.2 入侵信号调制原理

1.2.1 入侵信号引起光在光纤中的相移

入侵信号是预警系统的主要检测对象,其信号源包括但不限于预警管道爆裂、人为挖掘行为、可疑份子或车辆进入预警区域边界等。当预埋光纤受入侵源应力、温度或振动的作用时,外界信号通过光纤的调制效应(如:弹光效应和热应变效应等)使光纤折射率、纤芯长度和纤芯内径发生变化,进而导致光在光纤中传输时相位改变,即实现环境变化对光波相位的调制。通过测量光波的相位改变即可获知相应的压力信号或振动信号。

设光纤长度为L,折射率为n,直径为D,光波通过光纤的相移

其中β为光纤传播常数,可近似表示为光纤折射率和直径的函数,由此有

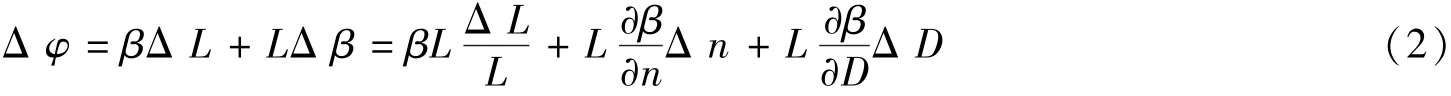
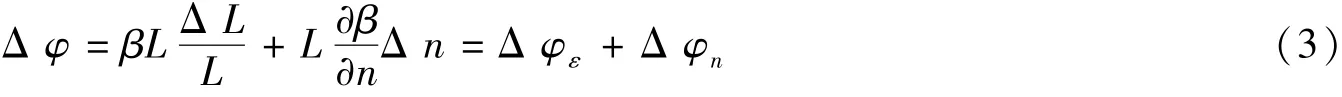
弹光效应引起的Δφs可采用应变力场下的材料相对介电抗张量的变化描述,再代入石英光纤的弹光张量和主应变张量可得到

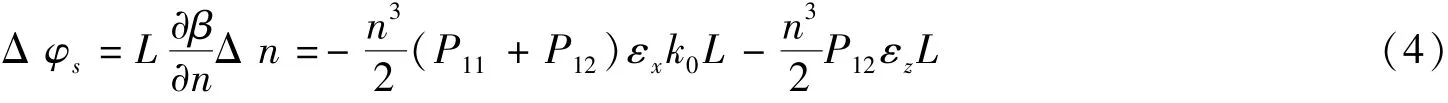
其中P12和P11为4阶弹光张量,k0为传播常数,εx和εz为光纤各向应变。

而对于光纤弹性变形引起的相位变化为

将式(4)和式(5)代入式(3),有

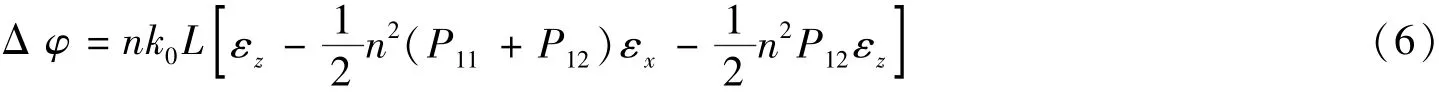
1.2.2 干涉型光纤预警系统相位调制原理

调制入侵信号的相移量Δφ可认为是时间t的函数,对其进行分析处理需利用干涉原理将光波信号的相位变化转换为光强变化,进而实现间接测量。设两光纤内光波经光纤相位调制后的振动函数E1、E2为

其中E0为光波振幅,ω为振动频率,α、β为初始相位。现假设其偏振态相等,则其矢量和为

故根据光的相干叠加原理,平均光强为

其中I0=E20表示光强;Δφ(t)=Δφ1-Δφ2表示调制相位;φ0=α-β表示初始相位。

通过光电转换将光纤两端的干涉光强信号I(t)转化为电压信号,再经由调理、A/D转换后进入上位机分析处理,即可识别与定位该光纤沿线上的入侵信号,进而达到利用光纤实现监测和预警的效果。

1.2.3 调制信号传输特性分析

根据1.2.2节分析,建立入侵信号的传输模型如图2所示。

图2 入侵信号传输模型框图Fig.2 Transmission model block diagram of intrusion signal

原始入侵行为引起的振动信号通过传感光纤调制在光信号的相位上,然后利用干涉原理转换为光强信号,最后经由光电转换电路调制为电压信号从而可被上位机处理。光波产生干涉应保持两束相干光的偏振态一致,但工程应用中由于纤芯的椭圆程度不均匀、内部残存应力以及光纤在成缆、铺设等过程中受到不确定外力和强磁场电场或是温度变化的影响,都会引起单模光纤的双折射,导致光在传输过程中其偏振态会产生缓慢随机变化,使已调相光波退化为椭圆偏振光,进而产生干涉信号对比度下降的“偏振诱导衰落”现象[13](见图3a)或干涉输出初相位(即式(2)中参数φ0)变化的“偏振诱导相位偏移”现象[14](见图3b,其中初相位φ0偏移量为π/3),由图3可看出,信号平均功率、均方根出现明显偏移且出现倍频以及基频衰减现象,使系统无法准确识别信号。同时相位偏移引起两路信号互相关性降低将严重影响系统定位准确度。

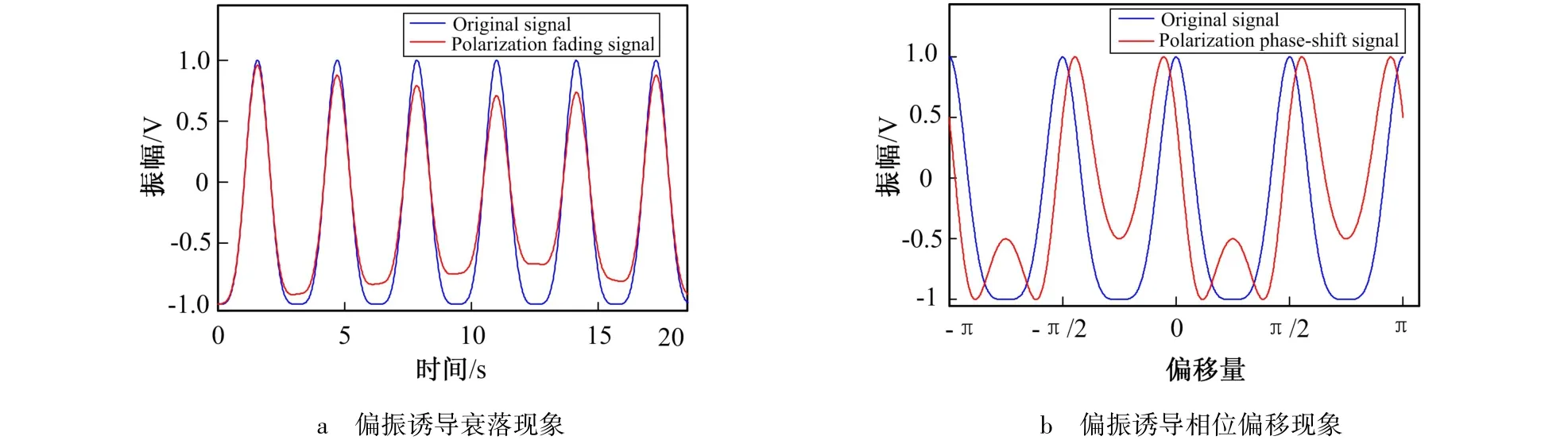
图3 干涉信号的偏振诱导衰落与偏振诱导相位偏移Fig.3 Polarization fading and polarization phase-shift of interference signal

抑制调制信号传输时因偏振退化导致特性改变的方法有两种:一是利用有源偏振控制动态补偿偏振衰落与相位偏移,但是响应时间较长,存在预警盲区,可靠性较差且成本较高,维护相对复杂;二是通过适当算法将调制在干涉信号中的原相位信号解调出来,从而遍历的消除偏振影响,系统相对简单,成本较低,适合工程应用。

2 基于3×3耦合器的信号解调原理

2.1 微分交叉相乘法

将图1中3×3耦合器C3近似为分光比为1 ∶1 ∶1的理想元件,光电探测器PB1、PB2、PB3检测到互成120°相位差的光强信号可表示为

其中I0为平均光强,光源稳定时为常直流量;A为干涉条纹峰值,受上述“偏振诱导衰落”现象影响是关于时间t的缓变量;φ(t)=φn(t)+φ0是待解调的相位信号,φ0为干涉输出初相位,受上述“偏振诱导相位偏移”现象影响且同为关于t的缓变量,φn(t)是环境引起的高频随机噪声。设在一次入侵振动中光纤各向应变εi是关于t的函数,代入式(6)得

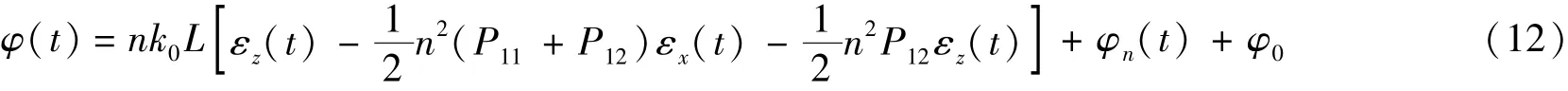
将满足式(11)的光强信号进过光电转换、放大并在满足奈奎斯特定理的条件下分别采样后通过电容隔直法消去直流量I0,得到3路电压序列可表示为

其中G为电路总增益,为推导方便,取G=1。利用3×3耦合器相位差特性,将3路分别平方并求和得

利用式(14)消去式(13)中参量A得

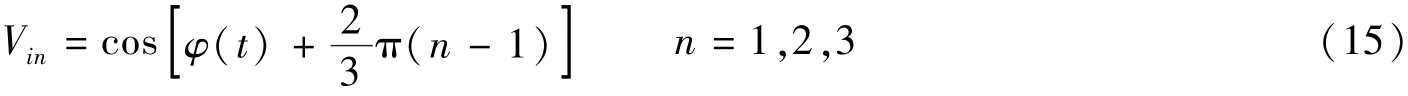
对满足式(15)的归一化调制信号使用微分交叉相乘法解调,其原理如图4所示。

首先将3路分别通过微分器得到

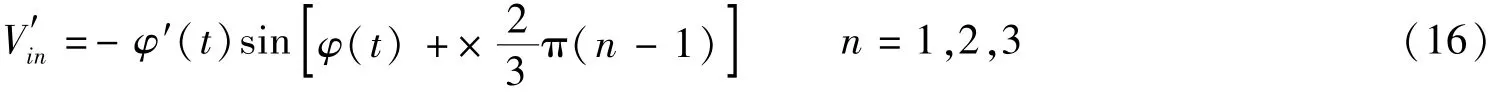
再将每路Vin分别乘以另外两路微分后的差,用积化和差公式化简得

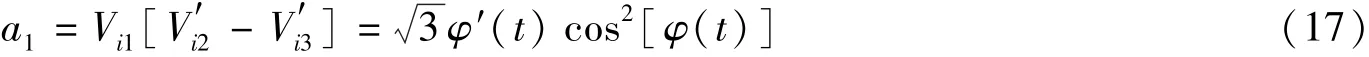
图4 微分交叉相乘法解调算法原理Fig.4 Algorithm principle of differential cross multiplication method

取3路和,得

然后通过积分器,取积分常量为零得

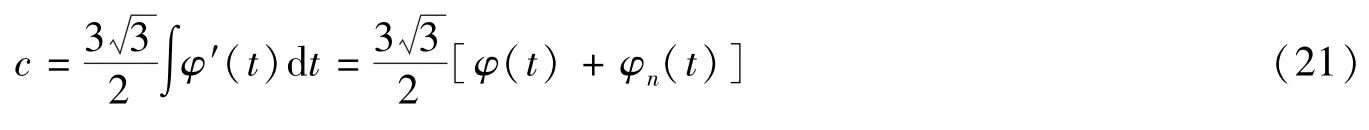
消系数后通过高通滤波器滤除高频噪声φn(t),即

2.2 非理想3×3耦合器的影响与调校

实际工程应用中,由于3×3耦合器受温度波动与制作工艺的限制,很难保持理想对称,即出现随机但可测量的不均匀分光比与偏移相差θ。不失一般性,可设光电探测器输出为

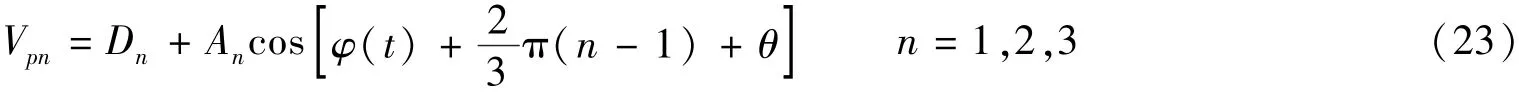
电容过滤直流量Dn的同时还将过滤待解调信号φ(t)的直流项,进而导致解调结果失真并降低系统动态响应范围[15]。An不均匀导致式(14)无法消去参数A,且式(14)中等号是否成立受偏差θ影响。为解决上述问题,常用方法是利用椭圆参数估计法分别对每组Dn、An构成的李萨如图形估计,然后将参数反解得出[16]。实际中,该参数在复杂的环境噪声下无法构成规则的李萨如图形,进而导致估计偏差且椭圆参数估计耗时较长,严重减慢解调速率。笔者提出结合光路与算法的“短时峰峰值检测法”(STPP:Short Time Peak-to-Peak)以调校参数Dn、An,其过程如下:将图1传感臂1处部分光纤缠绕在压电陶瓷(PZT:Piezoelectric Ceramic Transducer)元件上数圈,再以大幅值正弦交变电压驱动PZT,致使该段光纤长度L、光纤纵向应变εz改变,由式(6)可知光纤内光信号将产生大于2π的相移量进而使干涉光强信号达到峰值,设短时间内某路光电探测器输出平均最大值为Vmaxi,最小值Vmini,有

由式(24)和式(25)分别校正每路输出参数An、Dn后得到带偏移相差θ归一化调制信号

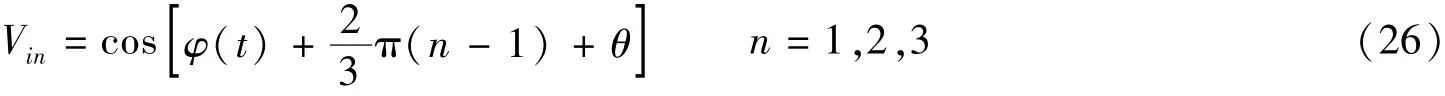
对满足式(26)的调制信号使用图3微分交叉相乘法解调时,偏移相差θ将导致式(20)改写为

其中

偏移相差θ仅受耦合器本征属性与传输光波长的影响,因此在系统中视为常量,可通过Bessel函数展开法精确计算,通常小于5°,由此构造φ(t)的幅值二元函数f(θ,φ(t))的三维函数图如图5所示。

由图5可以看出,取耦合器相位偏差θ=5°时,幅度函数f(θ,φ(t))出现随φ(t)取值改变的系统误差,其平均绝对百分比误差(MAPE:Mean Absolute Percentage Error)值为6.71%,相对标准偏差(RSD:Relatives Standard Deviation)值为7.45%,且该偏差θ对φ(t)的频率与相位无影响,故对系统后续的模式识别与系统定位影响极小。

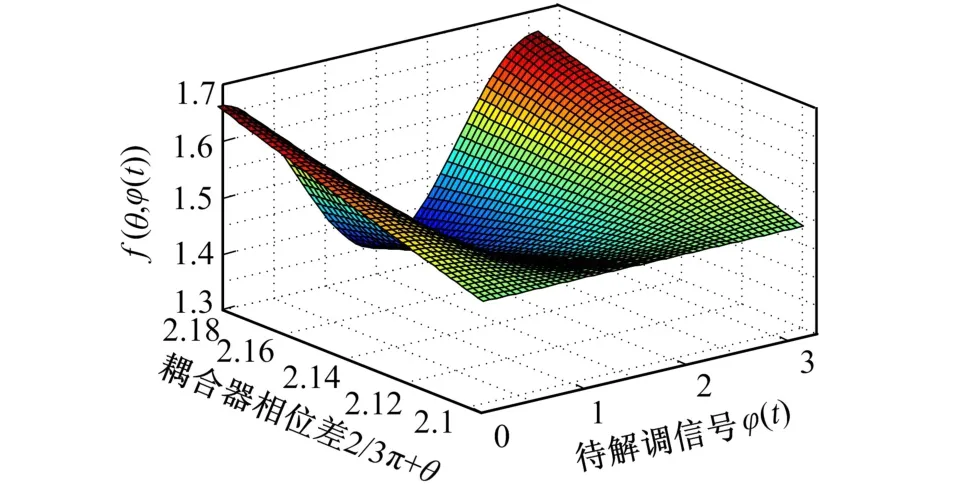
图5 幅值二元函数f(θ,φ(t))Fig.5 Amplitude binary function f(θ,φ(t))

3 仿真分析

3.1 微分交叉相乘解调算法抗偏振退化性能

解调算法最重要的作用是抑制调制信号传输时因偏振退化导致的特性改变,微分交叉相乘解调算法Simulink仿真模型图如图6所示,其中包括实现式(14)的归一化调校模块与实现图4解调功能的归一化信号解调模块。

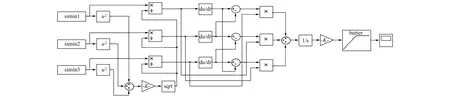
图6 微分交叉相乘解调算法仿真模型图Fig.6 Simulation block diagram of differential cross multiplication method

为分析抗偏振诱导衰落现象与抗偏振诱导相位偏移现象性能,取单频简谐信号φ(t)=πcos(2πft)作为原始相位信号,对图3a中偏振诱导衰落信号进行解调,结果如图7a所示,对图3b中偏振诱导相位偏移信号进行解调,结果如图7b所示。

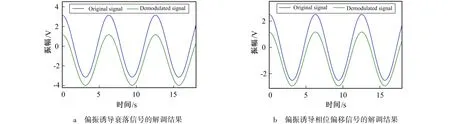
图7 偏振诱导衰落信号与偏振诱导相位偏移信号的解调结果Fig.7 Demodulation result of polarization fading signal and polarization phase-shift signal

由图7可以看出,解调结果复原出原始信号且存在幅值平移,是由于算法中积分常数选取不同而导致。而单纯的幅值平移对系统后续的信号识别与定位不产生影响,即该算法能有效解调相位信号且具有抗偏退化性能。

3.2 非均匀3×3耦合器对结果的影响

由于实际3×3耦合器存在可测定的不均匀分光比与偏移相差导致解调前参数调校误差,进而导致解调失真。因此取耦合器输出3路存在1.4 dB分光比偏差及10°偏移相差,为控制变量,使用上述φ(t)作为原始信号,分别使用式(14)经典法与STPP归一化调校后仿真解调,结果如图8所示。

由图8可看出,使用STPP调校后在再使用微分交叉相乘法解调的结果没有出现原解调结果的轻度失真纹波,表明在实际耦合器存在一定程度非均匀性的条件下,该方法解调质量较好,保真度较高。

3.3 解调含有高次谐波的相移信号

上述仿真均建立在原始相移信号取单频简谐信号的假设下,而在实际工程中发现,振动引起的相移信号含有大量高次谐波。同时,被动型无载波的微分交叉相乘解调法理论上具有良好的动态响应范围,设φ(t)=5cos(2πft)+2sin(6πft)+cos(16πft),取f=250 Hz。为控制变量,设耦合器均匀且无偏振退化,仿真解调结果如图9所示,解调后仅包含少量幅值增益误差,能准确的还原含有高次谐波的原始信号。

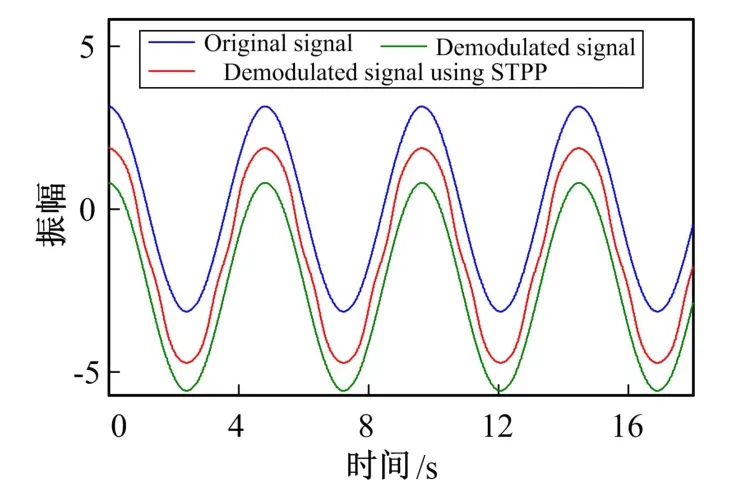
图8 当耦合器不均匀时,直接解调结果与用STPP后解调结果Fig.8 Demodulation result using and not using STPP when the coupler is unbalanced

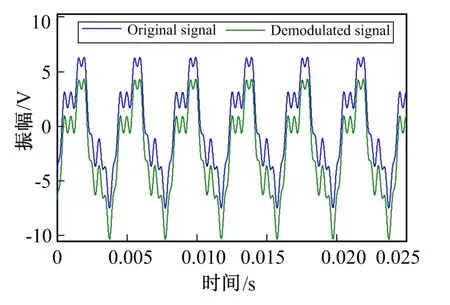
图9 含高次谐波的输入信号 与解调结果Fig.9 Demodulation result of input signal existing high order harmonics

4 结 语

笔者在干涉型光纤预警系统结构的基础上,从分析入侵信号调制理论入手,结合实际中普遍存在的偏振退化现象,提出解调技术在工程应用方面的重要性,详细推导了实用价值较高的微分交叉相乘解调算法,并提出STPP以调校实际中非理想3×3耦合器的不均衡参数。从Simulink仿真结果可看出,该解调方案可克服偏振退化引起的干扰,解调结果基本不受非理想3×3耦合器的影响,具有良好的鲁棒性以及宽动态响应范围,为干涉型光纤预警系统的工程应用提供了重要指导。

[1]崔洪亮,于淼,常天英,等.应用于海洋环境和海洋工程的光纤传感技术 [J].吉林大学学报:地球科学版,2017,47(1):279-293.CUI Hongliang,YU Miao,CHANG Tianying,et al.Fiber Optic Sensing Technology for Applications in Marine Environment and Marine Engineering[J].Journal of Jilin University:Earth Science Edition,2017,47(1):279-293.

[2]廖延彪,黎敏.光纤光学[M].北京:清华大学出版社,2013.LIAO Yanbiao,LI Min.Optic Fiber[M].Beijing:Tsinghua University Press,2013.

[3]CULSHAW B,KERSEY A.Fiber-Optic Sensing:A Historical Perspective[J].Journal of Lightwave Technology,2008,26(9):1064-1078.

[4]姜霁珊,江毅,刘达,等.基于双M-Z干涉仪的光纤周界防护系统[J].光学技术,2015,41(3):193-196.JIANG Jishan,JIANG Yi,LIU Da,et al.Fiber-Optic Perimeter Security System Based on Dual Mach-Zehnder Interferometer Structure[J].Optical Technique,2015,41(3):193-196.

[5]LI R,WANG X,HUANG J,et al.Spatial-Division-Multiplexing Addressed Fiber Laser Hydrophone Array[J].Optics Letters,2013,38(11):1909.

[6]喻骁芒,罗光明,朱珍民,等.分布式光纤传感器周界安防入侵信号的多目标识别 [J].光电工程,2014,41(1):36-41.YU Xiaomang,LUO Guangming,ZHU Zhenmin,et al.The Multi Target Recognition of Intrusion Signal of Perimeter Security with Distributed Fiber-Optic Sensor[J].Opto-Electronic Engineering,2014,41(1):36-41.

[7]张春熹,李勤,李立京,等.基于Sagnac组合型干涉仪的光纤分布式扰动传感器(英文)[J].红外与激光工程,2014,43(10):3378-3382.ZHANG Chunxi,LIQin,LI Lijing,et al.Fiber-Optic Distributed Disturbance Sensor Based on Merged Sagnac Interferometers[J].Infrared and Laser Engineering,2014,43(10):3378-3382.

[8]吴娇.Mach-Zehnder干涉仪在石油管道监控中的应用[D].北京:北京交通大学电子信息工程学院,2012.WU Jiao.Application of the Mach-Zehnder Interferometer in Monitoring Oil Pipelines[D].Beijing:School of Electronic and Information Engineering,Beijing Jiaotong University,2012.

[9]MA C,LIU T,LIU K,et al.A Continuous Wavelet Transform Based Time Delay Estimation Method for Long Range Fiber Interferometric Vibration Sensor[J].Journal of Lightwave Technology,2016,34(16):3785-3789.

[10]LEE B.Review of the Present Status of Optical Fiber Sensors[J].Optical Fiber Technology,2003,9(2):57-79.

[11]DANDRIDGE A,TVETEN A B,GIALLORENZI T G.Homodyne Demodulation Scheme for Fiber Optic Sensors Using Phase Generated Carrier[J].IEEE Transactions on Microwave Theory&Techniques,2003,30(10):1635-1641.

[12]陈宇,林京,孟强.基于3×3耦合器光纤水听器的数字化解调方案[J].仪器仪表学报,2008,29(4):755-759.CHEN Yu,LIN Jing,MENG Qiang.Digitized Demodulation Scheme of Fiber Optical Hydrophones Based on 3×3 Coupler[J].Chinese Journal of Scientific Instrument,2008,29(4):755-759.

[13]刘悦,蒋鹏,马丽娜,等.干涉型光纤传感系统偏振切换技术原理及实验研究 [J].激光与光电子学进展,2015,52(12):60-65.LIU Yue,JIANGPeng,MA Lina,et al.Experimental Research on Fiber Optical Sensing System Based on Interferometer with Polarization Switching[J].Laser&Optoelectronics Progress,2015,52(12):60-65.

[14]FORESTIERI E,VINCETTIL.Exact Evaluation of the Jones Matrix of a Fiber in the Presence of Polarization Mode Dispersion of Any Order[J].Journal of Lightwave Technology,2002,19(12):1898-1909.

[15]张雅彬,窦峥,曹家年.干涉型光纤水听器三路输出解调方案研究 [J].哈尔滨工程大学学报,2004,25(6):732-735.ZHANG Yabin,DOU Zheng,CAOJianian.3-Output Demodulation of Interferometric Fiber-Optic Hydrophone[J].Journal of Harbin Engineering University,2004,25(6):732-735.

[16]毛欣,黄俊斌,顾宏灿.采用3×3耦合器的分布反馈式光纤激光传感器解调技术 [J].发光学报,2017,38(3):395-401.MAO Xin,HUANG Junbin,GU Hongcan.Demodulation Technology of Distributed Feedback Fiber Laser Sensor on 3×3 Coupler[J].Chinese Journal of Luminescence,2017,38(3):395-401.