共信道时频重叠的数字信号调制识别方法
陈思南,龚晓峰,陈利波
(四川大学 电气信息学院,四川 成都 610065)
0 引 言
近年来,随着无线电通信环境的日益复杂化,通信信号的自动调制识别也随之引起了越来越多的关注[1]。日益密集的通信环境使得无线电频谱监测接收机在同一个信道中有时会捕获到多个时频重叠的信号分量,这将给后续的信号处理带来很多的困难[2,3]。因此,研究共信道时频重叠的数字信号调制识别具有重要的实际意义和应用价值。
目前已有的多信号调制识别方法主要分为信号的分离识别[4,5]和直接提取待识别多信号的特征这两种方法。其中文献[6]利用循环频率特征时频重叠双信号进行了有效识别,但前提是必须保证分量信号的载频和符号速率不同;文献[7]采用了四阶循环累积量特征的识别方法,对时频重叠多信号进行了有效识别,但在低信噪比的情况下识别率不高;文献[8]提出的利用信号的瞬时自相关特性和谱相关特征的方法,能够在低信噪比情况下得到较高的识别率,但是可识别信号的类型仅限于MPSK信号。针对这些问题,本文通过数字信号提取高阶累积量特征和瞬时特征值,实现了由4种数字信号组合而成的10种数字调制双信号的有效分类,并在较低信噪比的情况下获得了较高的识别率。
1 信号模型
在实际应用中,接收机接收到信号往往夹杂着一些噪声,收到的受噪声污染过的数字调制信号模型[9]可以表示为
(1)
式中:n=1,2,3,…,N,N为发送码元序列的长度,Es为发送码元波形的功率,hn为发送的码元序列,g(t)以及Ts分别表示发送的码元波形和宽度,fc和θc是载波的频率和相位,假设n(t)是与信号相互独立的复高斯白噪声,且均值为零。
首先对接收机得到的原始信号进行相应的预处理,从而得到经过定时同步、载波频率和相位同步以及下变频处理后的基带信号,可以将其复数形式表示如下
(2)
根据数字信号不同的调制方式,分别将MASK和MPSK两种数字调制信号经过下变频处理后的信号表示为

(3)

(4)
式(3)表示的是MASK信号,式(4)表示的是MPSK信号,其中M表示调制方式为M进制。
根据上面构建的信号模型,将本文研究的时频重叠的双信号表示如下
r(t)=s1(t)+s2(t)+n(t)
(5)
式中:s1(t) 和s2(t) 分别表示2ASK、4ASK、QPSK、8PSK其中的任意一种调制方式的数字信号。
2 特征参数分析
2.1 高阶累积量
k阶平稳随机过程{x(t)}的k阶累积量[10]定义如下
Ckx(τ1,τ2,…,τk-1)=
cum(x(t+τ1),x(t+τ2),…x(t+τk-1))
(6)
式中:cum(.)表示求累积量。
对于一个均值为零的复平稳随机信号x(t),它的p阶混合矩定义为
Mpq=E[x(t)p-qx*(t)q]
(7)
式中:E[.]表示求期望运算,*表示对随机序列取共轭运算,q表示其取共轭序列的个数。
因此,随机信号的二阶、四阶和六阶累积量分别表示如下
C20=cum(x,x)=M20
(8)
(9)
C41=cum(x,x,x,x*)=M41-3M20M21
(10)
(11)

(12)
在式(5)所表示的双信号模型中信号s1(t)、信号s2(t) 以及高斯白噪声n(t)均为相互独立的,所以根据高阶累积量的半不变性可得
cum(r(t))=cum(s1(t))+cum(s2(t))+cum(n(t))
(13)
由于零均值高斯白噪声大于二阶累积量的值为零,所以可以将式(13)改写成
cum(r(t))=cum(s1(t))+cum(s2(t))
(14)
从式(14)中可以看出从高阶累积量中提取的特征参数不受噪声的影响,因此该方法能够有效地抑制噪声,并对信号的调制方式进行识别。假设s1(t)和s2(t)两个信号的功率相同且未知,用符号Es表示。并且利用式(8)~式(12)计算出10种待识别的数字双信号的二阶累积量和四阶累积量见表1。

表1 待识别信号二阶、四阶累积量的理论值
2.2 瞬时特征值
由表1可以看出MASK类时频重叠双信号的高阶累积量比较相近,所以很难利用高阶累积量的特征将其有效识别。针对这个问题,考虑采用 “零中心归一化瞬时幅度绝对值的标准偏差[11]”这个瞬时特征参数对该子类进行识别,定义如下
(15)
式中:N为采样点数,Acn(i)为零中心归一化的瞬时幅度。
因为不同的MASK信号的瞬时幅度变化有很大的不同,进制数越多,其零中心归一化瞬时幅度标准偏差的值也越大,所以利用此特征参数可以轻松地将由2ASK和4ASK组成的3种时频重叠双信号有效地识别。
3 调制方式识别
3.1 特征参数提取
为了避免相位抖动对高阶累积量产生的影响,因此选用高阶累积量的绝对值。同时为了消除信号功率大小对高阶累积量产生的影响,所以高阶累积量的特征参数采用了比值的形式[12]。本文提取的4个高阶累积量特征参数如下
(16)
(17)
(18)
(19)
本文将这些基于高阶累积量的特征参数用于时频重叠双信号识别。根据式(14)以及表1的高阶累积量的理论值,计算各特征参数的理论值见表2。
3.2 算法步骤
利用表2中的4个特征参数再结合瞬时特征参数σaa共5个特征参数,并采用决策树判决方法对10种时频重叠的双数字信号进行识别,如图1所示:
(1)先对信号进行预处理。
(2)利用特征参数F1将信号分为{2ASK+2ASK,2ASK+4ASK,4ASK+4ASK }、{QPSK+QPSK,QPSK+8PSK,8PSK+8PSK}和{2ASK+QPSK,2ASK+8PSK,4ASK+QPSK,4ASK+8PSK}3类。
(3)再利用特征参数F2识别出QPSK+QPSK,QPSK+8PSK,8PSK+8PSK。

表2 待识别信号累积量参数的理论值
(4)然后利用特征参数σaa识别出2ASK+2ASK,2ASK+4ASK,4ASK+4ASK。
(5)接着利用特征参数F3将剩下的信号分为{2ASK+QPSK,4ASK+QPSK}和{2ASK+8PSK,4ASK+8PSK}两类。
(6)最后利用特征参数F4识别出2ASK+QPSK,4ASK+QPSK,2ASK+8PSK,4ASK+8PSK。
至此,所有10种数字双信号调制方式的识别全部完成。

图1 信号识别分类
4 仿真结果
4.1 特征参数对比
根据上述分析,对本文提出的算法进行计算机仿真实验。设信号的载波频率是150 kHz,其采样率为1200 kHz,码速率为12 kHz,截取信号的码元个数为2048。用计算机对该算法进行10 000次的独立蒙特卡洛实验,并取平均值作为最终结果。图2为10种双信号在不同信噪比下特征参数F1的值,可以看出其很明显将这10种信号分为了3个子类。图3为第一个子类中的3种双信号在不同信噪比下特征参数F2的值,从中可以看出在信噪比大于-5 dB时,参数F2逐渐趋于稳定,并且接近理论值,说明该特征参数可以将QPSK+QPSK、QPSK+8PSK、8PSK+8PSK这3类双信号有效区分。
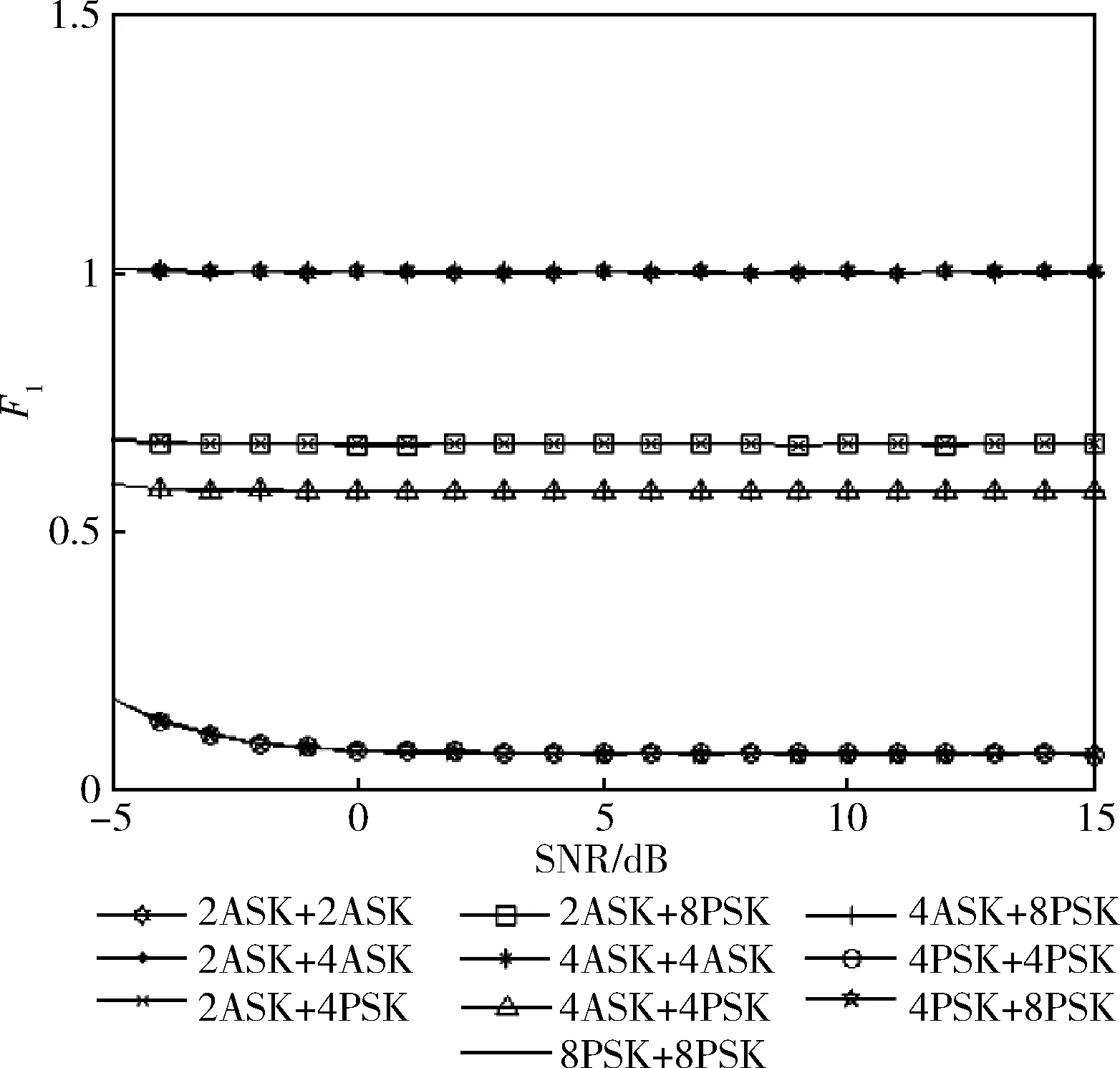
图2 特征参数F1的值
图4是特征参数σaa在不同信噪比下的值,虽然瞬时特征值受信噪比影响较大,但是从图中可以看出在信噪比大于0 dB时该特征参数已经可以有效地识别出2ASK+2ASK、2ASK+4ASK、4ASK+4ASK这3类信号。图5为不同信噪比下特征参数F3的值,可以看出其很明显将剩下的4类待识别信号分为了两个子类。
图6和图7是2ASK+QPSK、4ASK+QPSK、2ASK+8PSK和4ASK+8PSK这4类信号的特征参数F4的值,从中可以看出这4类信号可以在较低的信噪比下被特征参数F4有效分类。

图4 特征参数σaa的值

图5 特征参数F3的值

图6 QPSK和MASK的F1值
4.2 不同信噪比下的识别正确率
根据图2~图7的仿真结果并设置相应的最佳门限值,对该算法进行10 000次的独立实验,得到的10种时频重叠双信号在不同信噪比下的最终识别结果如图8所示。
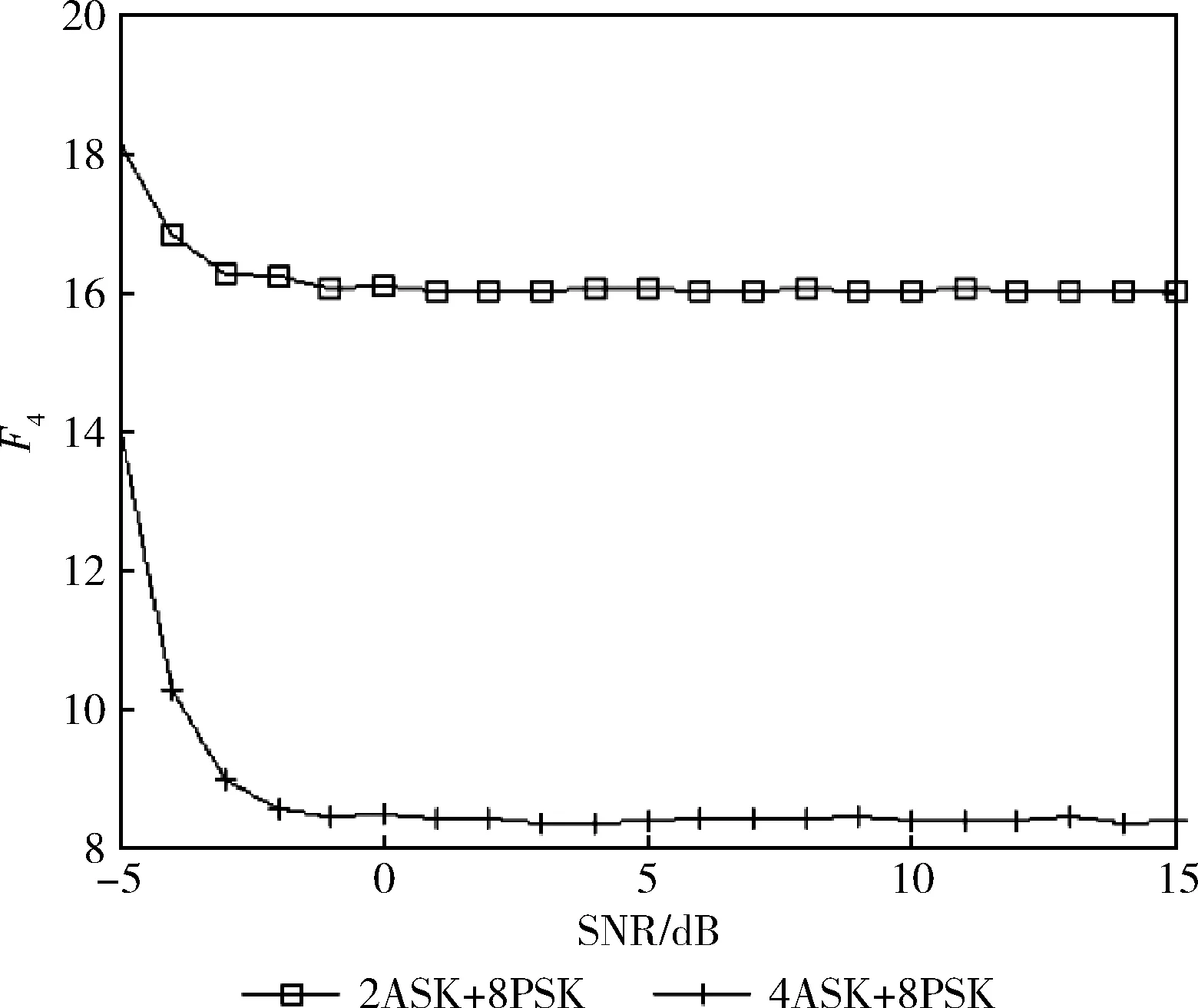
图7 8PSK和MASK的F4值
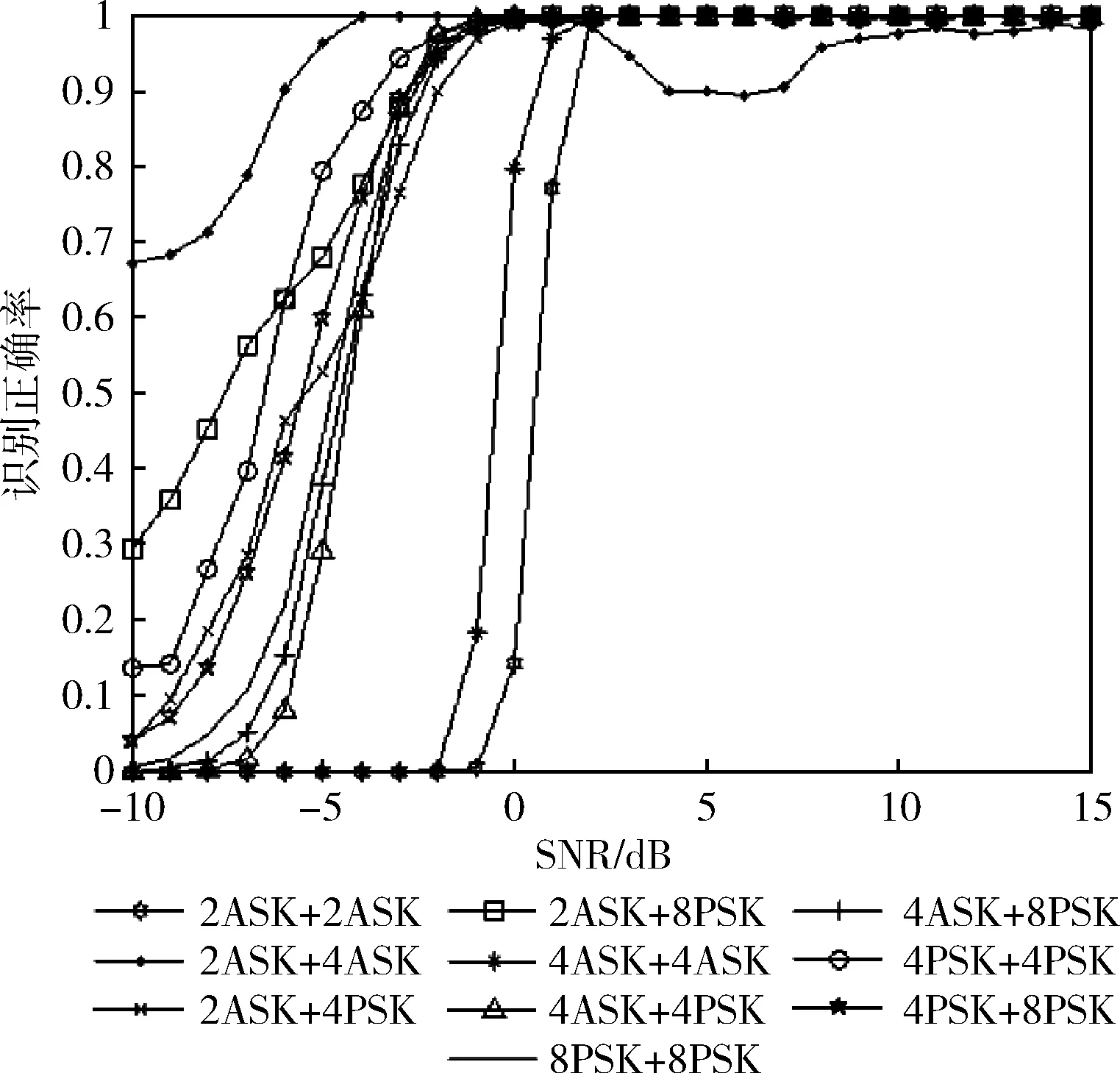
图8 不同信噪比下的识别率
从仿真结果中可以得到在信噪比为5 dB的情况下,信号的平均识别率已经达到99%,并且在信噪比大于10 dB的情况下,平均识别率已经达到了100%。表3是将文献[7]和文献[8]的算法与本文算法进行对比,可以看出本文算法在增加识别种类的情况下,信号识别正确率仍然有所提高。
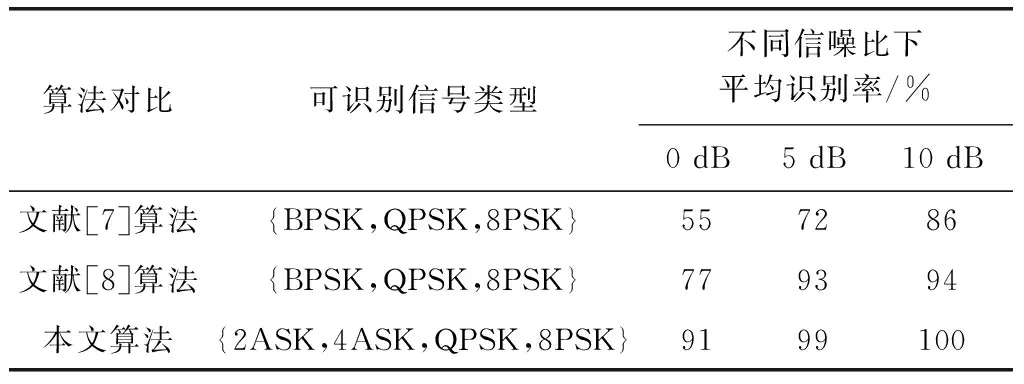
表3 不同方法识别类型和识别效果对比
5 结束语
本文将数字信号的高阶累积量特征值与瞬时特征参数相结合,应用在与功率相同的时频重叠双信号的调制识别。利用高阶累积量对噪声的不敏感性和MASK的瞬时特征值可分性强的特点,有效地将10种时频重叠双信号进行分类。本文的算法对比与已有算法增加了2ASK和4ASK两种可识别信号的类型,并且实验结果表明在低信噪比为0 dB情况下将信号的平均识别率提高到了91.13%。但是针对信号功率不同和载频不同的情况,以及时频重叠多信号的数字调制识别还需进一步研究,并且在识别率方面仍然存在一定的提升空间。
[1]WANG Lanxun,GUO Shuting,JIA Cengjuan.The digital modulation recognition technique based on the wavelet envelope difference[J].Application of Electronic Technique,2017,43(2):95-98(in Chinese).[王兰勋,郭淑婷,贾层娟.基于小波包络差异性的数字调制方式识别技术[J].电子技术应用,2017,43(2):95-98.]
[2]ZHI Yajing,CHEN Xiao,CAI Tingting.Blind separation method of single channel time-frequency overlapped gauss amplitude modulation signals[J].Science Technology and Enginee-ring,2016,16(1):204-208(in Chinese).[支亚京,陈晓,蔡婷婷.单通道时频重叠高斯调幅通信信号盲分离方法[J].科学技术与工程,2016,16(1):204-208.]
[3]LI Bingbing,MA Hongshuai,LIU Mingqian.Carrier frequency estimation method of time-frequency overlapped signals with alpha-stable noise[J].Journal of Electronics & Information Technology,2014,36(4):868-874(in Chinese).[李兵兵,马洪帅,刘明骞.Alpha稳定分布噪声下时频重叠信号的载波频率估计方法[J].电子与信息学报,2014,36(4):868-874.]
[4]Lu W,Zhang B.Single channel time-varying amplitude LFM interference blind separation using MHMPSO particle filtering[C]//IEEE International Conference on Signal and Image Processing Applications,2013:425-430.
[5]Pang L,Tang B.Single channel blind signal separation of time-frequency overlapped signals based on independent component analysis[C]//International Conference on Communications,Circuits and Systems.IEEE,2013:147-151.
[6]ZHAO Yufeng,CAO Yujian,JI Yong,et al.Modulation identification for single-channel mixed communication signals based on cyclic frequency features[J].Journal of Electronics & Information Technology,2014,36(5):1202-1208(in Chinese).[赵宇峰,曹玉健,纪勇,等.基于循环频率特征的单信道混合通信信号的调制识别[J].电子与信息学报,2014,36(5):1202-1208.]
[7]LI Kuangdai,GUO Lili,SHI Rong,et al.Modulation recognition method for single-channel time-frequency overlapped MPSK signals[J].Fire Control & Command Control,2010,35(2):150-153(in Chinese).[李旷代,郭黎利,石荣,等.单信道时频重叠MPSK信号的调制识别方法[J].火力与指挥控制,2010,35(2):150-153.]
[8]ZENG Chuangzhan,JIA Xin.A modulation recognition me-thod for time-frequency overlapped MPSK signals in single channel[J].Science Technology and Engineering,2016,16(5):172-176(in Chinese).[曾创展,贾鑫.一种单信道时频重叠多进制数字相位调制信号调制识别方法[J].科学技术与工程,2016,16(5):172-176.]
[9]GUO Juanjuan,YIN Hongdong,JIANG Lu,et al.Recognition of digital modulation signals via high-order cumulants[J].Communication Technology,2014,47(11):1255-1260(in Chinese).[郭娟娟,尹洪东,姜璐,等.利用高阶累积量实现数字调制信号的识别[J].通信技术,2014,47(11):1255-1260.]
[10]LIU Mingzhu,ZHAO Yue,SHI Lin,et al.Researchon recognition algorithm of digital modulation by higher order cumulants[C]//Fourth International Conference on Instrumentation and Measurement,Computer,Communication and Control,2014:686-690.
[11]HUANG Yong.Simulation research and implementation of automatic modulation recognition algorithm of communication signal[D].Chengdu:University of Electronic Science and Technology of China,2013:7-10(in Chinese).[黄勇.通信信号的自动调制识别算法仿真研究与实现[D].成都:电子科技大学,2013:7-10.]
[12]ZHAO Xiongwen,GUO Chunxia,LI Jingchun.Mixed recognition algorithm for signal modulation schemes by high-order cumulants and cyclic spectrum[J].Journal of Electro-nics & Information Technology,2016,38(3):674-680(in Chinese).[赵雄文,郭春霞,李景春.基于高阶累积量和循环谱的信号调制方式混合识别算法[J].电子与信息学报,2016,38(3):674-680.]

