浅谈高考数学创新问题应对策略
赵金波 任成亚
(吉林省永吉实验高中,吉林 永吉)
一、问题特点
统观近几年数学高考试题,创新题频繁出现。主要以新运算、新概念和新背景形式给出命题。要求学生不仅有扎实的基础知识、基本方法,还要有较强的阅读能力、分析转化能力、逻辑推理能力、抽象概括能力和良好的数学综合素养。由于试题新颖对每个考生公平、公正有利于选拔优秀人才。
二、常见问题
1.新运算:所指通过数学中符号语言、图形语音、文字语言给出新的运算模型,要求考生根据模型结合所学知识点、方法和数学思想去探究,求解结论。
例 1.2015浙江(理 6)设 A,B 是有限集,定义 d(A,B)=card(A∪B)-card(A∩B),其中 card(A)表示有限集 A 中的元素个数
命题①:对任意有限集 A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集 A,B,C,d(A,C)≤d(A,B)+d(B,C),A.命题①和命题②都成立 B.命题①和命题②都不成立C.命题①成立,命题②不成立 D.命题①不成立,命题②成立
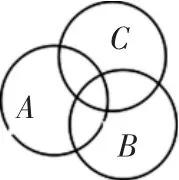
试题解析:命题①显然正确,通过右图可知a(A,C)表示的区域不大于 d(A,B)+d(B,C)的区域,所以命题②也正确,故选A
例2.2013湖北(理14)古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10,…,第n个三角形数为记第 n个 k边形数为 N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
……可以推测N(n,k)的表达式,由此计算 N(10,24)= 。
试题解析:观察n2和n前面的系数,可知一个成递增的等差数列另一个成递减的等差数列,故 N(n,24)=11n2-10n,∴N(10,24)=1000
点评:从上述例题可以得出此类问题的研究。首先根据运算模型把问题转化为集合、向量、数列的相关知识,再利用恒等代入、数形结合、归纳猜想等方法去解决实际问题。
2.新概念:是指利用数学问题的表述形式在一定限制条件下,给出一个问题新的定义,从而要求考生探究新概念下问题属性。
例1.2017全国I(理12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们退出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列 1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推。求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂。那么该款软件的激活码是 ( )
A.440 B.330 C.220 D.110
例 2.2016 四川(理 15)在平面直角坐标系中,当 P(x,y)不是原点时,定义P的“伴随点”为当 P是原点时,定义P的“伴随点“为它自身,平面曲线C上所有点的“伴随点”所构成的曲线C′定义为曲线C的“伴随曲线”。现有下列命题:
①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A;
②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”C′关于y轴对称;
④一条直线的“伴随曲线”是一条直线。
其中的真命题是_____(写出所有真命题的序列)。
试题解析:
解法二:由定义可知p(x,y)伴随点p(′x′,y′)应满足x′2+y′2=所以①④错误,②③正确。
点评:从前面问题可以总结出探究此类问题,首要细致理解定义,把握住限制条件,再确定所用知识点如数列、圆锥曲线,然后结合本知识点研究问题的方法,适当合理选用方法去解决问题。
三、总结梳理
针对创新问题研究策略,笔者认为,首先应掌握运算模型、理解定义,分析出新背景下含义,把问题转化为相关的数学知识点与方法上,再构建恰当模型后求解结论。应注意从正反两个角度分析探究问题,创新问题。不仅对学生数学知识方法、思想和能力做全面考查,而且对数学文化作一定的考查,能达到让学生形成良好的数学素养的目的。

