Measurement of lumber moisture content based on PCA and GSSVM

Jiawei Zhang•Wenlong Song•Bin Jiang•Mingbao Li

Introduction

Lumber moisture content(LMC)is an important measured variable in the wood drying process.Its precision directly affects the drying quality,the cost,and the drying time of the wood(Martinovic et al.2001;Klaric and Pervan 2012).Many of the important properties of wood depend considerably on moisture content which can vary widely depending on environment and history(Zhang et al.2003).

Although the LMC is a signi fi cant indicator of the drying control system,normally it is too dif fi cult to build the moisture content model to control the wood drying process precisely due to that wood drying system shows characteristics of large time delay,strong coupling and nonlinear(Awadalla et al.2004;Zhang et al.2006;Skuratov 2008;Isaksson and Thelandersson 2013).The wood drying moisture content prediction model could provide the precise and real-time moisture content data for optimizing the drying process and have considerable meaning for improving the drying control level.

To improve the measuring accuracy and reliability of LMC,the optimal support vector machine(SVM)algorithm was put forward for regression analysis LMC.Environmental parameters such as air temperature and relative humidity,were considered,the data of which were extracted with the principle component analysis(PCA)method.The regression and prediction of SVM was optimized based on the grid search(GS)technique.Groups of data were sampled and analyzed,and simulation comparison of forecasting performance shows that the main component data were extracted to speed up the convergence rate of the optimum algorithm.The GS-SVM gives a better performance in solving the LMC measuring and forecasting problem.Therefore,exploring the scienti fi c and effective way is not only of research signi fi cance and of practical value for analyzing the data of moisture content changes in the course of drying,but it also will help operators reasonably adjust the drying course and improve the level of the drying process.

SVM,originally developed by Vapnik,is a powerful tool of statistical learning for solving problems in nonlinear classi fi cation,function estimation and density estimation(Rakotomamonjy 2007;Diosan et al.2010;Pouteau and Collin 2013).SVM is based on a risk minimization principle,which means that the empirical risk and con fi dence range is considerable;therefore,the output of the model is an optimal solution(Nelson et al.2008;Roy and Bhattacharya 2010;Tarjoman et al.2013).SVM has been extensively studied and has shown remarkable success in many applications,including soft sensors,multi-sensor,and data fusion.SVM could solve the problems of partial minimum and over learning in neural networks due to extrapolation generalization capability in the case of small samples.Considering that the penalty factor c and kernel function parameter g could affect the complexity and generalization ability of the SVM model,it is necessary to choose the optimization parameter.The optimized c and g was found by the GS method,which could improve the learning ef fi ciency and generalization ability,and ensure the effectiveness and accuracy of the LMC prediction model(Ataei and Osanloo 2004;Fox et al.2001;Rodi 2006;Beyramysoltan et al.2013;Liu and Jia 2013).PCA was used to pretreat wood drying data as sample data had more noise in the drying process,and the SVM could not distinguish samples from being redundant,useful or not in the training process.

Materials and methods

Case study and data

Cottonwood wood was chosen for the drying experiment(Zhang et al.2006).The kiln was 2.5 m×1.5 m×1.2 m and the size of each piece of lumber was 2.4 m×0.2 m×0.05 m.Before the drying experiment,the original moisture content was determined and lumber with the same moisture content was put on the same layer,and each layer was isolated by the plate to ensure the wind could get at the surface of each piece of lumber.The detection point was chosen randomly in the cottonwood lumber pile.Air temperature and relative humidity were continuously monitored by two temperature sensorsT1andT2,and two humidity sensorsE1andE2.Six LMC sensors were located sequentially at the detection point.The distance between two sensors was 10 cm.The measured pointsMC1,MC2,…,MC6were monitored automatically.Ten dimension vectors of experimental data were sampled and employed for regression analysis.Among them,T1andT2,E1andE2,MC1,MC2,…,MC6,that is 9 dimensions were used as the independent variables of regression analysis andMC6as the dependent variable.

Experimental data were sampled at the same intervals.Among them,50 samples were selected for regression analysis,in which 1–40 were used as SVM model training samples,and 41–50 for regression forecast with the tested SVM model.The comparison between the experimental data and the forecast results allowed the SVM regression forecast performance to be evaluated.

Principle component analysis(PCA)

PCA is one of the multivariate statistical methods which can be used to reduce input variables complexity when there is a large volume of information(Camdevyren et al.2005;Noori et al.2010a,b,c).PCA changes the input variables into principal components(PCs)that are independent and linear of input variables(Lu et al.2003).Instead of the direct use of input variables,we transform them into PCs and then they may be used as input variables.With this method,the information on input variables will be presented with minimum losses in PCs(Helena et al.2000;Noori et al.2012).Details for mastering the art of PCA are published by Noori et al.(2007).

PCA is intended to have a better interpretation of variables(Noori et al.2009a,b,2010a,b,c).In mathematical terms,PCA involves the following steps:(1)start by coding the variablesX1,X2,…,Xpto have zero means and unit variance;(2)calculate the correlation matrix R;(3)fi nd the eigenvalues λ1,λ2,…,λpand the corresponding eigenvectorsa1,a2, …,apby solving|R-Iλ|=0.(4)discard any components that only account for a small proportion of the variation in data sets;(5)develop the factor-loading matrix and perform a Varimax rotation to infer the principal parameters(Ouyang 2005;Noori et al.2010a,b,c).

GS method description(GS)

The GS method belongs to a type of digital planning method which is often used to solve nonlinear optimization problems with constraints.The GS method has no special requirement in function and could search for the value of multiple target parameters.The method could eventually develop a set of optimal combination of parameters.Each optimal value would be searched in the corresponding region.The search region with the constraint conditions is divided into grids at fi xed intervals.Each grid intersection point which is a match or a mismatch condition point corresponds to a value of the objective function.Because the match condition points could be good points or bad points,all match condition points have had a comparative analysis on some principles and then the grid intersection point of the optimal objective function is obtained(Ataei and Osanloo 2004).The value of the parameters corresponding to the intersection point is the optimal parameter value in totality;c and g are two important parameters of the forecasting model which was built by SVM(Patra and Bruzzon 2014).

Support vector machine(SVM)regression

The basic idea of the SVM regression is to map input data into a feature space via a nonlinear map.In the feature space,a linear decision function is constructed.The SRM principle is employed in constructing the optimum decision function.SVM nonlinearly maps the inner product of the feature space to the original space via kernels.The SVM nonlinear regression algorithms are reviewed in this section.

Given a set of training data （x1,y1）,...,（xl,yl）∈Rn×R,the nonlinear function ψ（x）is employed to map original input spaceRnto higher dimensional feature spaceRk:ψ（x）= （φ（x1）,φ（x2）,...,φ（xl））, wherek（k≫n）represents the dimension of feature space.Then an optimum decision functionf（xi）= ωφ（xi）+bis constructed in this higher dimensional feature space,where ω=（ωl,...,ωk）is a vector of weights in this feature space(Dahmani et al.2014;Huang 2009;Kuang et al.2013).Nonlinearfunction estimation in the originalspace becomes a linear function estimation in feature space.By the SRM principle,we obtain the optimization solution(Wang 2005;Noori et al.2009a,b):

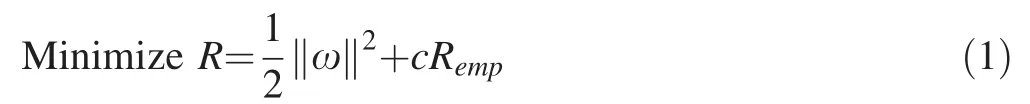
subject to

where ξiandare slack variables and ε is the accuracy demanded for the approximation.The solution to this optimization problem is given by the saddle point of the Lagrangian(Noori et al.2015):

(minimum with respect to elements ω,b, ξi,andand maximum with respect to Lagrange multipliersai＞0,＞0, βi＞0,i=1,...,l). From the optimality conditions

and,

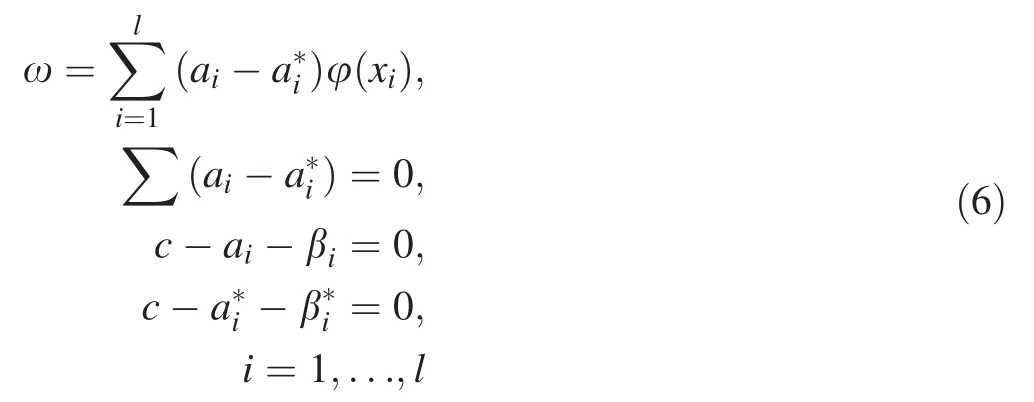
By(4)and(6),the optimization problem can be rewritten as:

subject to,

Finally,a nonlinear function is obtained as:

The kernel functions treated by SVM are functions with linear,polynomial or Gaussian radial basis,exponential radial basis,and splines(Chen and Xie 2007;Noori et al.2011;Salvador and Chou 2014).The Gaussian radial basis function used in this study can be de fi ned as:where g is the Gaussian radial basis kernel function width.

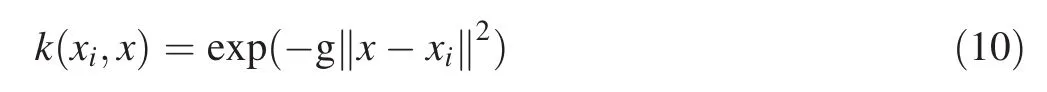
The advantages of the Gaussian radial basis kernel function are that it is computationally simpler than the other function types and nonlinearly maps the training data into an in fi nite dimensional space(Subasi 2013).Optimizing parameters will become complex polynomial basis function or sigmoid function because two variables need determination in polynomial basis function and sigmoid function,respectively.Thus,it can handle situations in which the relation between input and output variables is nonlinear.

Results

PCA for LMC data processing

Principal component analysis is used to analyze the relationship among the nine dimension data sets of independent variables on principle components.The purpose is the guaranteed loss minimum from the original data information,under the premise of the original data attributes to mix into a group of new unrelated comprehensive indices,which is the simpli fi ed original data to improve the training precision of the SVM model and the ef fi ciency of the regression forecast.Principle component analysis schematic diagram for LMC is shown in Fig.1 which is from Matlab 7.0 simulation software.

Experimental data are normalized and combined linearly.The original 9 dimension data sets,namely 90 measured parameters,are transferred into 3 principle components reduction sets which are rearranged according to contribution rate.The simulation results are shown as Fig.1.The most important components of the variance contribution rate is 89.7%,the second principal rate is 4.9%,and the third accounted for 2.8%.Factor analysis was performed for 9 LMC traits of 90 sampled data to select the top 3 factors whose cumulative contribution of variance accounted to 97.4%,which can describe mathematically the performance of LMC compared to physical factors.

Fig.1 Principle component analysis schematic diagram for LMC

SVM regression analysis based on grid searching technique(GS)

The GS method searched the global optimal value of c and g according to the given step in a rectangular range.The concrete steps of implementation were as follows:

(1) The search scope and step size of c and g were set in the GS method and then a two-dimensional grid was structured in coordinates systems of c and g.

(2) The data collected from drying experiment was used as a sample set and divided into n groups.Arbitrary n-1 sets of data were chosen as training samples and the remaining set chosen as prediction sample.From the two-dimensional grid coordinate system,arbitrarily one set of parameters,which included c and g,was chosen to train n-1 sets of data and then predict 1 set of data(Cross-validation technique).The prediction error of the LMC was recorded.

(3) Step(2)was repeated until all c and g were trained once in a two-dimensional grid.

(4) MSE was the evaluation criterion of the prediction accuracy corresponding to each c and g.MSE,c and g constituted a three-dimensional coordinate system in which MSE was shown by contour.Ultimately,the optimal parameter value of c and g were determined when MSE obtained minimum.

The fl owchart of LMC prediction based on GS and SVM is presented in Fig.2.

Fig.2 The fl owchart of LMC prediction based on GS and SVM

The original,normalized and PCA dimension reduction data were used for training and testing under the condition that the optimal parameters c and g of SVM were obtained by the grid searching technique.For the three different data sets,training and testing results were analyzed.To ensure the reliability of the contrast,grid setting parameters were kept consistent under the three training conditions.The parameters of the searching technique were set as follows:40 samples were divided into fi ve sets averaged through cross validation.The grid size was set to 0.5,namely 2-1,the parameters c and g of the optimum range were 2-8-2+8.

Model training and regression testing for original data

With the original data,the parameters were optimized by the grid search technique is shown as Fig.3.The range of log2c is represented by X axis and Y axis.The variation of mean square error is shown by the Z axis.The parameters c and g are optimized from the beginning of 2-8.MSE is gradually converged from the red numerical area,and the optimization process is fi nished until c and g reach 28,which is shown with the blue numerical area.Mean square error is CVmse=0.0009 with the cross validation and the optimal parameter c=32,g=0.0039 for SVM

GS-SVM regression and predicted curve is shown in Fig.4.X axis means independent variables of sampled data,Y axis is the estimating value of LMC.From the train set regression prediction by SVM,‘○’is the true value ofMC6used as training data. ‘□’represents 1–40MC6predicting value estimated from 450 sampled points of 9 dimension data sets.From the test set regression predict,we conclude that ‘◇’is the true value ofMC6used as testing data.‘*’represents 41–50MC6predicting values estimated from 50 sampled points of 1 dimension data sets.Mean square error is mse=0.0002 and curve goodness of fi t isr2=0.9988 with the training model.Mean square error is mse=0.0105 and curve goodness of fi t isr2=0.9296 with the regression testing.The computation time of entire operation process was 4.13 s.

Model training and regression testing for PCA data

With the original data,the parameters are optimized by the PCA-GS(principle components analysis method combining grid search technique)is shown in Fig.5.The range of log2c is represented by the X axial and the Y axial.The variation of mean square error is shown by the Z axial.The parameters c and g are optimized from the beginning of 2-8.MSE is gradually converged from the red numerical area,and optimization process is fi nished when c and g reach 28,shown with blue numerical area.Convergence speed is increased with the data preprocessed by PCA.Mean square error is CVmse=0.0008 with the cross validation and the optimalparameterc=11.3137,g=0.0884 for SVM.

PCA-GS-SVM regression and predict curve is shown in Fig.6.X axis means independent variables,Y axis is the estimating value of LMC.From the train set regression predict by SVM, ‘○’is the true value ofMC6used as training data.‘□’represents 1–40MC6predicting value which is estimated from 120 sampled points of 3 dimension principle components.From the test set regression predict by SVM,we conclude that ‘◇’is the true value ofMC6used as testing data.‘*’represents 41–50MC6predicting value estimated from PCA data.Mean square error is mse=0.0001,curve goodness of fi t isr2=0.9994 with the training model.Mean square error is mse=0.0039,curve goodness of fi t isr2=0.9214 with the regression testing.The computation time of the whole operation process was 3.09 s.

The simulation results shown as the previous four diagrams are analyzed comparably.We conclude that the convergence speed of the grid searching method increases under the condition that the experimental data are preprocessed by the principle components analysis method.Again,the performance of curve fi tting is superior to that without PCA.

Comprehensive analysis on error performance index

In order to validate training error and prediction deviation,the three indexes,mean square error(MSE),curve goodness-of- fi t(r2),and consumption time(t),are a measure of predictive ability for discrete data space.Among them,TmseandTr2represent training error and training curve goodness-of- fi t,respectively.PmseandPr2indicate the prediction error and goodness-of- fi t forecasting curve.

Table 1 is the error index analysis on GS-SVM with the sampled data sourced from the original experiment datawith PCA dimension reductions.Comparing and analyzing the data processing in Table 1 shows that SVM forecasting precision is improved and algorithm running time is shortened with PCA dimension reduction.

Fig.3 Three-dimensional simulation diagram on GS(Grid searching technique)

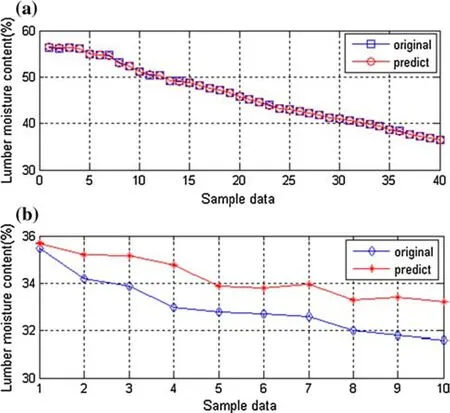
Fig.4 GS-SVM regression and predicted curve.a Train set regression predict by SVM,b test set regression predict by SVM

TmseandTr2represent training error and training curve goodness-of- fi t,respectively.PmseandPr2indicate the prediction error and goodness-of- fi t forecasting curve.

The error analysis indexes(Table 1)is SVM modeling based on the sampled data processed by grid searching technique.Although GS disadvantages are lower ef fi ciency and longer running time for the exhaustion method as the basic principle,it can fi nd global optimal parameters exactly.The simulation results show that GS-SVM modeling has higher ef fi ciency with the premise of SVM forecasting accuracy.

Discussion

We used relative parameters from experiment data to establish multidimensional data collection according to the high correlation between lumber moisture content and medium temperature and moisture in the course of drying.To solve the problem that the large difference of each feature quantity’s data level in fl uences the regression analysis function,the method of data feature normalization is proposed to pretreat the data so as to unify each feature quantity’s lumber dryness multidimensional data and improve the regression analysis function of the lumber moisture content.This paper proposes PCA from dimensionality reduction for the feature extraction for the normalized lumber dryness data.It results in the optimization for multidimensional data,the improvement of the quality of data and utilization rate regression and also the improvement of analysis ef fi ciency of lumber moisture content.

SVM has the characteristic of solving the problems of nonlinearity,high dimensionality,and uncertainty.Because of lumber dryness parameter collection is redundant and uncertain this paper establishes lumber moisture content regression model based on support vector machine for thedata of lumber moisture content,temperature,and moisture to predict.While doing regression predictions with SVM,the values of penalty parameter c and kernel function parameter g will directly in fl uence the regression prediction function of the support vector machine.This paper utilizes grid search intelligent algorithm to optimize c and g.

Fig.5 Three-dimensional simulation diagram on PCA-GS

Fig.6 PCA-GS-SVM regression and predict curve.a Train set regression predict by SVM,b test set regression predict by SVM

Table 1 Error index analysis on GS-SVM

Conclusion

There is often a complex nonlinear relationship between LMC and environmental factors in the drying process.To solve this problem,a novel intelligent computation method based on PCA and GS-SVM was proposed.To decrease data redundancy,dimension reduction was realized by the PCA method by which the sampled multi-dimension data are optimized.The optimum parameters of SVM global optimization is obtained from GS.From the experimental data and simulation results,GS-SVM with principle component analysis gives a better performance in solving the interference problem from the environmental factors during the LMC accuracy measurement.

Ataei M,Osanloo M(2004)Using a combination of genetic algorithm and the grid search method to determine optimum cutoff grades of multiple metal deposits.Int J Surf Min Reclam Environ 18:60–78

Awadalla HSF,El-Dib AF,Mohamad MA,Reuss M,Hussein HMS(2004)Mathematical modelling and experimental veri fi cation of wood drying process.Energy Convers Manag 45:197–207

Beyramysoltan S,RajkóR,Abdollahi H(2013)Investigation of the equality constraint effect on the reduction of the rotational ambiguity in three-component system using a novel grid search method.Anal Chim Acta 791:25–35

Camdevyren H,Demyr N,Kanik A,Keskyn S(2005)Use of principal component scores in multiple linear regression models for prediction of Chlorophyll-a in reservoirs.Ecol Model 181:581–589

Chen GY,Xie WF(2007)Pattern recognition with SVM and dualtree complex wavelets.Image Vis Comput 25:960–966

Dahmani H,Selouani S,Doghmane N,O’Shaughnessy D,Chetouani M(2014)On the relevance of using rhythmic metrics and SVM to assess dysarthric severity.Int J Biom 6:248–271

Diosan L,Rogozan A,Pecuchet JP(2010)Learning SVM with complex multiple kernels evolved by genetic programming.Int J Artif Intell Tools 19:647–677

Fox SB,Culha M,Sepaniak MJ(2001)Development of a grid search molecular mechanics modeling strategy to study elution behavior in cyclodextrin modi fi ed capillary electrophoresis.J Liq Chromatogr Relat Technol 24:1209–1228

Helena B,Pardo R,Vega M,Barrado E,Fernandez JM,Fernandez L(2000)Temporal evolution of groundwater composition in an alluvial aquifer(Pisuerga river,Spain)by principal component analysis.Water Res 34:807–816

Huang SC(2009)Integrating nonlinear graph based dimensionality reduction schemes with SVMs for credit rating forecasting.Expert Syst Appl 36:7515–7518

Isaksson T,Thelandersson S(2013)Experimental investigation on the effect of detail design on wood moisture content in outdoor above ground applications.Build Environ 59:239–249

Kecman V (2005)Support vector machines:an introduction.Springer,Berlin

Klaric M,Pervan S(2012)Improving of maintenance of humidifying system in conventional wood kiln dryers.Drv Ind 63:87–94

Kuang YC,Yu JQ,Hu YC,Wang Y(2013)Research and application of real estate document image classi fi cation based on SVMs and KNN.J Inf Comput Sci 10:6093–6100

Liu PY,Jia KB(2013)A motion-characteristics-based unsymmetrical-cross multi-hexagon-grid search algorithm for fast motion estimation.Inf Technol J 12:3128–3133

Lu WZ,Wang WJ,Wang XK,Xu ZB,Leung AYT(2003)Using improved neural network to analyze RSP,NOx and NO2 levels in urban air in Mong Kok,Hong Kong.Environ Monit Assess 87:235–254

Martinovic D,Horman I,Demirdzic I(2001)Numerical and experimental analysis of a wood drying process.Wood Sci Technol 35:143–156

Nelson JDB,Damper RI,Gunn SR,Guo B(2008)Signal theory for SVM kernel design with applications to parameter estimation and sequence kernels.Neurocomputing 72:15–22

Noori R,Kerachian R,Khodadadi A,Shakibayinia A(2007)Assessment of importance of water quality monitoring stations using principal component and factor analyses:a case study of the Karoon River.J Water Wastewater 63:60–69

Noori R,Abdoli MA,Ameri-Ghasrodashti A,Jalili-Ghazizade M(2009a)Prediction of municipal solid waste generation with combination of support vector machine and principal component analysis:a case study of mashhad.Environ Prog Sustain Energy 28:249–258

Noori R,Abdoli MA,Jalili-Ghazizade M,Samifard R(2009b)Comparison of ANN and PCA based multivariate linear regression applied to predict the weekly municipal solid waste generation in Tehran.Iran J Public Health 38:74–84

Noori R,Karbassi AR,Sabahi MS(2010a)Evaluation of PCA and Gamma test techniques on ANN operation for weekly solid waste predicting.J Environ Manag 91:767–771

Noori R,Khakpour A,Omidvar B,Farokhnia A(2010b)Comparison of ANN and principal component analysis-multivariate linear regression models for predicting the river fl ow based on developed discrepancy ratio statistic.ExpertSystAppl 37:5856–5862

Noori R,Sabahi MS,Karbassi AR,Baghvand A,Zadeh HT(2010c)Multivariate statistical analysis of surface water quality based on correlationsand variations in the data set.Desalination 260:129–136

Noori R,Karbassi AR,Moghaddamnia A,Han D,Zokaei-Ashtiani MH,Farokhnia A,Gousheh MG(2011)Assessment of input variables determination on the SVM model performance using PCA,Gamma test,and forward selection techniques for monthly stream fl ow prediction.J Hydrol 401:177–189

Noori R,Karbassi AR,Khakpour A,Shahbazbegian M,Badam HMK,Vesali-Naseh M(2012)Chemometric analysis of surface water quality data:case study of the gorganrud river basin,Iran.Environ Model Assess 17:411–420

Noori R,Deng Z,Kiaghadi A,Kachoosangi F(2015)How reliable are ANN,ANFIS,and SVM techniques for predicting longitudinal dispersion coef fi cient in natural rivers?J Hydraul Eng 142:04015039

Ouyang Y(2005)Evaluation of river water quality monitoring stations by principal component analysis. Water Res 39:2621–2635

Patra S,Bruzzon L(2014)A novel SOM-SVM-based active learning technique for remote sensing image classi fi cation.IEEE Trans Geosci Remote Sens 52:6899–6910

Pouteau R,Collin A(2013)Spatial location and ecological content of support vectors in an SVM classi fi cation of tropical vegetation.Remote Sens Lett 4:686–695

Rakotomamonjy A(2007)Analysis of SVM regression bounds for variable ranking.Neurocomputing 70:1489–1501

Rodi W(2006)Grid-search event location with non-Gaussian error models.Phys Earth Planet Inter 158:55–66

Roy K,Bhattacharya P(2010)Improvement of iris recognition performance using region-based active contours,genetic algorithms and SVMs.IntJ Pattern RecognitArtifIntell 24:1209–1236

Salvador CM,Chou CCK(2014)Analysis of semi-volatile materials(SVM)in fi ne particulate matter.Atmos Environ 95:288–295

Skuratov NV(2008)Intelligent wood drying control:problems and decisions.Drying Technol 26:585–589

Subasi A(2013)Classi fi cation of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders.Comput Biol Med 43:576–586

Tarjoman M,Fatemizadeh E,Badie K(2013)An implementation of a CBIR system based on SVM learning scheme.J Med Eng Technol 37:43–47

Theodoros E,Tomaso P,Massimiliano P(2002)Regularization and statistical learning theory for data analysis.Comput Stat Data Anal 38:421–432

Vapnik VN(1998)Statistical learning theory,2nd edn.Wiley,New York

Wang L(2005)Support vector machines:theory and applications.Springer,Berlin,pp 1–48

Zhang DY,Liu YQ,Jun C(2003)Application of single neuron adaptive PID controller during the process of timber drying.J For Res 14:244–248

Zhang DY,Sun LP,Cao J(2006)Modeling of temperature-humidity for wood drying based on time-delay neural network.J For Res 17:141–144