多表面LED二次光学透镜设计的偏折能力分配法

周士康，陈春根

(上海三思科技发展有限公司，上海 201100)

引言

LED透镜都至少有两个光学表面。但大多数LED透镜的计算方法只能计算单个自由曲面的形状。如偏微分方程法[1]、剪裁法[2]、间断法[3]、连续法[4]，这些方法都是把其中一个表面做成球面的，这样就只需设计一个表面了。这样做的缺点是一个面的“负担”太重了，光学设计质量必然下降，有些设计任务则完成不了。光通量线方法提出了同时设计两个表面的方法[5]，用分配每个面“负担”的方法解决了这个问题。

这种方法还可以推广到多透镜即两个以上透镜的同时计算。

我们可能首先想到用多透镜会使光线损失增加，对正入射光线来说，由于表面多了，损失是会变大，但对斜入射光线来说，多透镜可能会反而减少光线的反射。我们知道，所有的光学表面都无法避免菲涅尔反射[6]，而且是入射角越大反射越多。在垂直入射时一般材料的表面反射率一般是4%左右，但入射角变大时，其反射率也变大。以材料折射率为1.5为例，射向透镜的光线当入射角为60°时反射率为10%。射离透镜的光线反射比射向透镜的反射更多，当入射角为30°时反射率就达到10%了，大角度时甚至会出现全反射。这说明反射率是应该考虑的重要问题，但已往的LED透镜光学计算中很少注意这一问题。这也是优秀的光学设计不采用大的入射角的原因。LED的透镜一般都是单个透镜，这样在要求偏折光线比较大的情况下，透镜的曲率变化就必须比较大，也就是说在透镜的边缘部分其入射角都会比较大。从菲涅尔反射定律知道，入射角度越大则反射越多。如果做成多透镜，虽然反射面增加了，反射也增加了，但由于面多了，每个面“担负”偏折光线的“责任”也小了。且这些面可以做成比较平坦，它们的菲涅尔反射也会在一定程度上减少。

另一方面，更重要的是，作为菲涅尔反射光学系统中杂散光的重要来源，菲涅尔反射的减少将降低杂散光的水平。

第三个好处是透镜的总重量会比单透镜大大减少。这在大口径透镜的情况下特别重要。一般可以减少重量40%。

第四个好处是减少注塑透镜的变形。LED透镜多数是注塑成形的，而大口径LED透镜不但重量大，而且中心和边缘的透镜厚度差也大，而零件厚度差大是注塑后变形的重要原因，这在大口径LED透镜中是一个严重问题。若使用多透镜则透镜的厚度差变小，变形也会变小。

多透镜也有明显的缺点，如正入射光线总反射多、结构复杂等，但从以上这些分析知道，在某些情况下将LED的透镜设计成多透镜组是有好处的。这就要求设计者做出合适的选择。

当然，多透镜另外一个缺点是在设计上将比单透镜更困难，但本文的方法可解决这一问题。本方法称为“偏折能力分配法”。简单说就是把对光线进行偏折的要求分配到每个表面。本方法还可以在不改变配光的情况下改变透镜的形状以适应不同设计的需求。

1 光通量线方法计算透镜形状

习惯上偏折角这概念用得比折射角少，但在本文中用偏折角却比较合适。偏折角被定义为光线的入射角和折射角之差。每个面都会引起光线偏折，各面引起的所有偏折角的和就是LED二次透镜的总偏折角。

本文的计算是基于非成像光学逆向计算自由曲面形状的光通量线方法[5]，其步骤可以结合图1简述如下：

图1 光通量线方法示意Fig.1 Schematic diagram of light flux ray method

1)把LED的光强分布按能量等分为n份，分割线就是透镜的n条入射线。n越大计算越精确，但这里简化为n=8。图1的左方给出LED的8条光通量线。它们是把LED的光通量分成相等的8份而求得的，代表的是方向。这8条入射线构成一个n=8的角度数列。

2)把照明的要求转换为能量在像面上的分布，不难求得透镜的n条出射光线角度数列，与入射线的数列一一对应。图1是以平行光输出为例的光通量线。

3)由上述n个“数列对”分别用折射定律求得n个“小面”。

4)连接这n个小面构成透镜表面。当n很大时就是一个平滑的透镜表面。

但是，以上的方法计算的是一个表面，这就相当于一个实际透镜的第2个面，而其第1面是必须是一个不对光线起偏折作用的球面。由于只有一个面，其偏折光的“负担”重，光线的入射角度很大。下面介绍如何让每一个面的“负担”减轻。

在求得透镜的入射线和出射线数列后，就求得了n个偏折角。把这n个偏折角按权重分隔成m份，m为透镜的表面数目，这就得到了个角度，也就是每个面前后的入射角和出射角。然后用文献[5]所述的光通量线方法可以一次性求得m×n个小面。当n足够大时就可得到平滑表面的透镜。这里m=2,4,6，…，就对应于单透镜、双透镜、三透镜等。下面还将看到，权重的给定方法还会影响透镜的形状。

下面以单透镜(m=2)为例用图形来简单说明在平均分配的情况下的偏折能力分配法。图2中左边的放射状线为从LED发出的光通量线，右方水平线为照明方的光通量线，本例中仍令n=8并以平行光出射为例。虚线与水平线的夹角就是偏折角，把这8个角再用8条点划线等分，这就得到了第3个角度数列，这就是透镜内部光通量线的角度。

图2 偏折角及偏折能力分配Fig. 2 Bending angle and distributing the bending light capacity

由这三个数列就可以按文献[5]的方法同时求得两个面n=8时的各8个小面的方向和位置，如图3所示。可以明显地看到，其光线的入射角比图1的小多了。

图3 单透镜的计算结果Fig.3 Calculating result of single lens

2 偏折能力分配法计算多透镜表面形状

偏折能力分配法设计多透镜的关键步骤就是给定每一个表面的偏折能力的权重，权重越大，则经过此面后的光线偏折越多。

2.1 双面单透镜的计算

令一个单透镜的两个表面的偏折能力的权重分别为C1和C2，两个面把所有光线分成了三部分，每部分都有n条光线，它们的角度为

θ1i,θ2i,θ3i(i=1，…，n)

(1)

其中：θ1i(i=1，…，n)为从LED发出的n条光线，由第1节的方法已经求得。θ(m+1)i(i=1，…，n)是最后一个面即第m面的出射的n条光线的出射角，也就是为满足照度分布而计算出的光通量线角度，也是已知的。按照偏折能力权重的定义，我们有

(2)

对n个i都成立。这样可以得到

(3)

这就得到了所有光通量线的角度。当两个面的权重相等时可得：

(4)

即等权重时θ2为总偏折角的角平分线。图3的情况实际上就是单透镜用等偏折角分配计算得到的例子。

2.2 多透镜的计算

推广到多透镜的情况，设表面数为偶数m，令m个面的偏折力的权重分别为

C1,C2,C3，…，Cm

(5)

每两个面之间的第i条光线角度为

θ1i,θ2i,θ3i，…，θ(m+1)i

(6)

其中，只有θ1i和θ(m+1)i为已知。由于本文的权重定义为对偏折角的权重，因此各面的单位权重引起的偏折角相同，即

(7)

式(7)对所有的i都成立。这样可以得到

(j=2，…，m,i=1，…，n)

(8)

许多情况下我们可令各面的权重相等，此时，把偏折角平分到每个面，则式(8)可简化为

(j=2，…，m,i=1，…，n)

(9)

多透镜的公式包含了单透镜，也就是当m=2时，式(8)和式(9)分别变为式(3)和式(4)。

计算m个表面形状得到n×m个小面的方法与上述两个表面时相同。

由于上述权重出现在比例式中，以上各面权重不需要归一。更有意思的是权重并不需要都是正数，也就是说允许“负”权重，其物理意义是光线反向偏折。下面第4节将介绍权重的大小和正负对透镜形状有很大影响，这种正负权重的设置方法也是偏折能力分配法的魅力所在。

3 无影灯双透镜的设计

LED的手术无影灯相比传统的卤素灯或环形节能灯有许多优点，越来越多的厂家开始生产LED的无影灯。由于无影灯要在一米远的位置形成一个最小半径只有0.05 m的光斑，其半光束角只有3°，这对LED是很高的要求。先估算透镜的大小，此时用一个超越几何光学的原理的光学扩展量(Etendue)来估计口径是很合适的。按照Etendue原理，n2πR2sin2θ在光学系统中是一个不变量，其中n为折射率，R为半径，θ为光束角。这意味着要达到的光束角越小则透镜的口径应该越大，这是任何光学系统都不能违反的原则。对LED为Nichia219的光源，用Etendue原理估算可得其透镜直径应该达到40 mm以上。

按前文的说明，对这样的透镜，做成双透镜是一个合适的选择。令四个面的偏折能力相等，按照上述方法计算的双面单透镜结果如图4所示。为了较清晰地显示光线走向，计算时取较少的光通量线数目n=100。

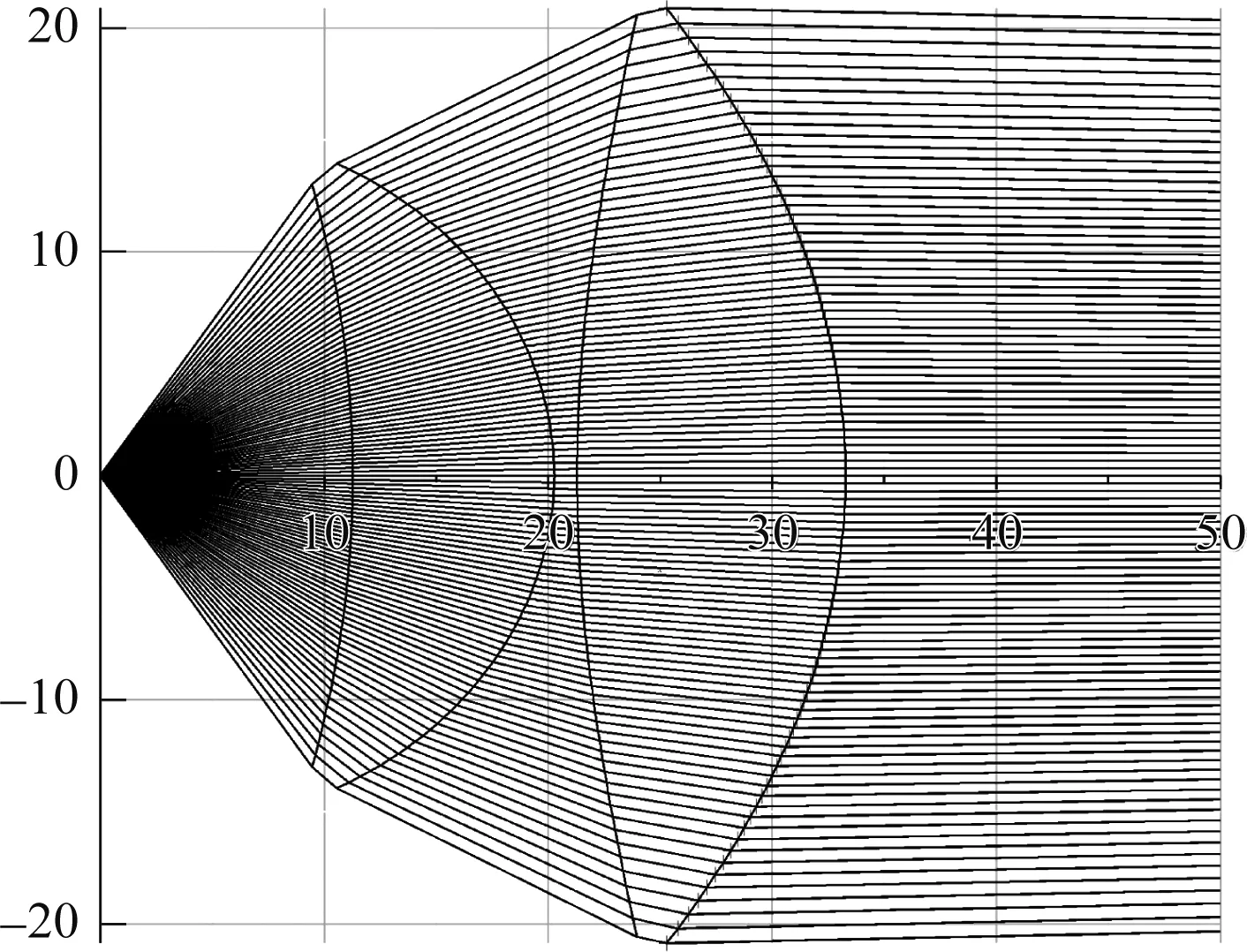
图4 无影灯双透镜计算结果Fig.4 Calculating result of double lenses of surgical luminaries

实际加工后的透镜组见图5。测量结果表明，双透镜的无影灯模块的光斑照度的“饱满度”、中心照度、光斑直径、照明深度、无影度等都能很好地满足国标的要求[7]。

图5 LED无影灯双透镜模组Fig.5 Double lenses module of LED surgical luminaries

透镜总重量为12 g，与同样照明要求时设计的单透镜相比重量减少了40%。而且由于中心和边缘的厚度差相对较小，其变形也比单透镜小得多。而且由于入射角小了，杂散光也少，照度分布也比较“干净”。虽然多了两个面，其表面反射和安装复杂性也会增加，但得到的光学性能的提高还是十分吸引人的。有关LED无影灯的设计方法见文献[8-9]中的介绍。

我们还计算了同样条件下的双面单透镜[图6(a)]和六面三透镜[图6(b)]的结果，这里取n=20。单透镜虽然简单，但单面菲涅耳反射大，重量大，注塑变形大，而三透镜虽然菲涅耳反射小，但总的小角度反射大，加工安装复杂。也可以不用全部透射式的，而是设计成内反射透镜(TIR)，但结果是尺度、杂散光、重量和变形都较大。综合考虑结果，我们还是采用了双透镜设计。

图6 无影灯单透镜和三透镜的计算结果Fig. 6 Calculating result of single and triplet lenses of surgical luminaries

4 用偏折能力权重控制透镜形状

前面已经提到，选择透镜两个面不同的偏折力权重C1,C2可以改变两个面的形状。为简单起见，以下还是以单透镜为例。图7以输出平行光为例给出了六种不同偏折力权重的透镜的计算结果，其中对应的偏折力权重分别为

(a)C1=-1，C2=4；

(b)C1=0，C2=1；

(c)C1=1，C2=4；

(d)C1=1，C2=1；

(e)C1=1，C2=0；

(f)C1=4，C2=-1。

计算方法都相同，只要简单地修改C1，C2的值就可以修改透镜的形状而不改变照明的要求。

图7 用偏折能力权重控制透镜形状Fig.7 Control lens shape by change the weight of bending light capacity

例如，情形(d)是常用的等权重的结果。情形(b)是C1=0的计算结果，相当于经过第1面的光线不偏折，也就是第1面为球面。情形(e)是C2=0的计算结果，在本例的平行光输出的要求下，得到的结果是第2面为平面。很有意思的是权重可以取负值，如情形(a)是入射面权重为负值，其结果是入射后的光线向反方向偏折。而情形(f)是出射面权重取负值，其结果是经过该面后面的光线向相反方向偏折。

这样，在同样的照明要求下，针对不同的装配要求，设计者有了更多的透镜形状的选择余地。

[1] DING Y, LIU X, ZHENG ZR, et al. Freeform LED lens for uniform illumination[J]. Opt Express, 2008, 16: 12958-12966.

[2] RIES H, MUSCHAWECK J. Tailoring freeform lenses for illumination[J]. Proc SPIE, 2001, 4442:43-50.

[3] WANG L, QIAN K, LUO Y. Discontinuous free-form lens design for prescribed irradiance[J]. Appl Opt, 2007, 46(18): 3716-3723.

[4] WANG K, WU D, CHEN F, et al. Angular color uniformity enhancement of white light-emitting diodes integrated with freeform lenses[J]. Opt Lett, 2010, 35(11): 1860.

[5] 周士康，陈春根，许礼，等. 光通量线方法用于LED二次光学设计[J]. 照明工程学报，2015, 27(1): 101-111.

[6] 李军依，王淑颖，李进，等. 菲涅耳公式的研究及数值模拟[J]. 大学物理实验，2016, 29(2):34-37.

[7] 国家医药行业标准:YY 0627—2008[S].

[8] 周士康，韩红梅，许礼，等. 改型高斯函数用于无影灯的照度模拟[J]. 照明工程学报，2015, 26(2): 86-93.

[9] 上海三思科技发展有限公司. 可变光斑LED无影灯的光学设计方法：201210165923.3[P].2017-04-19.