基于修正的BP神经网络算法对桩基承载力预测方法研究

徐华荣，刘刚

(1.镇江市勘察测绘研究院，江苏 镇江 212008； 2.镇江技师学院，江苏 镇江 212113)

1 前 言

桩基础在现代土木工程中的应用越来越广，尤其是在中国东南沿海地基承载力较小的地区，深桩基础对传递上部结构荷载有着非常重要的作用。在岩土工程勘察阶段，能够提早较准确预测桩基承载力不仅有利于选取适宜的桩基设计参数，节约成本，还可以为后续工期节省大量时间。

对桩基承载力的预测可分为应力控制方法和位移控制方法两种[1]。前者由桩-土间相互作用的最大应力经修正后确定承载力，后者则由桩基的荷载-沉降位移曲线得出。应力控制方法包括荷载传递法、数值模拟方法、静力触探(CPT)方法和孔压静力触探(CPTU)方法，如DeRuiter和Beringen法(欧洲法)[2]、Bustamante和Gianselli法(法国法)[3]、Meyerhof法[4]、Tumay和Fakhroo法[5]、Schmertmann和Nottingham法[6]等。位移控制方法有弹簧理论法、t-z曲线法、波动方程方法、经验公式方法以及静载试验法等。

近年来，学者们针对土的各种物理力学参数对桩基承载力的影响开展了大量的工作，对桩-土相互作用的机理也给出了许多研究成果，但由于桩-土相互作用是一个随时间和空间变化的动态系统，且受到多种因素的影响，具有很大的变异性和不确定性，得到的理论成果也是包含多个影响参数的解析解或半解析解，需要进行各种假设才能得出具体结果，对于岩土工程技术人员来讲，不具有实用性。

为了弥补在岩土工程领域理论研究的不足，原位测试技术在预测桩基承载力方面得到了迅猛发展，地震波静力触探(SCPTU)就是在静力触探(CPTU)基础上发展而来的一种新型的原位测试方法，主要运用于黏性土、粉土和砂性土层，在探头贯入过程中能够实时获得锥尖阻力(qc)、锥体摩阻力(fs)、剪切波速(vs)以及孔隙水压力(u0)四个沿桩长变化的连续数据指标。运用这些数据不仅能够预测桩基的轴向承载力，还能以此得到土层的剪切刚度(G)[1]，进而求出地基土沉降变形，为地基承载力提供设计和变形参数。尽管如此，GwizdalaK[7]指出了目前无论从理论还是实践方面，对于桩基承载力的预测都还存在一些问题和不足。要想得到相对精确的结果尚需借助于一些新型的方法或模型来进行模拟和预测。

神经网络算法便是其中之一，早在上世纪末就被学者们应用于岩土工程领域。Goh[8，9]提出了预测黏土中桩侧摩阻力的人工神经网络模型，随后Goh[10，11]又给出了预测砂土中打入桩的极限承载力，发现落锤高度、锥重、桩长、桩身材料对预测的结果影响较大；Abu-Kiefa[12]引入了3个神经网络模型来预测无黏性土中桩的受力情况，分别预测桩的总承载力、桩侧摩阻力和桩端阻力，得到了预测结果离散度最小的神经网络模型。Shahin et al[13]提出了预测地基沉降的神经网络模型。F.Pooya etc[14]基于人工神经网络利用标准贯入试验数据对桩基承载力做了预测，并讨论了贯入击数、荷载大小、桩身材料，嵌入长度等对桩基沉降的影响，结果表明贯入击数影响最明显，得到的预测结果准确率达到97.2%。蒋建平等[15]用RBF神经网络模型以土的塑性指数、含水率、孔隙比、密度为输入参数，预测了地基土的e-p曲线，得到了较好的预测结果。张丽萍等[16]基于小波概率神经网络预测了单桩竖向承载力，预测的结果与静载试验的结果相吻合。但从现有的研究来看，神经网络算法还存在以下不足之处Mohamed A[17]：①缺少促进人工神经网络发展的理论基础。②对岩土工程参数的处理和确定还没有一个统一的标准。

本文基于神经网络应用中存在的不足，进行了相应的完善工作。通过MATLAB程序，编制了相应的修正BP神经网络算法模型，对桩基竖向承载力进行了预测，并结合工程实际，与传统方法的预测结果进行了比较。

2 BP神经网络算法的介绍

BP神经网络是人工神经网络的一个分支，它以人工智能为模板，通过自觉的学习，训练，来实现非线性映射的能力，特别适合求解内部机制复杂的问题，广泛应用于分类识别、逼近、回归、预测等领域。

BP神经网络算法的步骤如下：

第一步：设置变量和参量：

Xk=[xk1，xk2，…，xkm]，(k=1，2，…，N)为输入向量，或称训练样本，N为训练样本的个数。

为第n次迭代时输入层与隐含层I之间的权值向量。

为第n次迭代时隐含层I与隐含层J之间的权值向量。

为第n次迭代时隐含层J与输出层之间的权值向量。

Yk(n)=[yk1(n)，yk2(n)，…，ykp(n)]，(k=1，2，…，N)为第n次迭代时网络的实际输出。

dk=[dk1，dk2，…，dkp]，(k=1，2，…，N)为期望输出。η为学习效率；n为迭代次数。

第二步：初始化，赋给WMI(0)，WIJ(0)，WJP(0)各一个较小的随机非零值。

第三步：随机输入样本Xk，n=0。

第五步：由期望输出dk和上一步求得的实际输出Yk(n)计算误差E(n)，判断其是否满足要求，若满足要求转至第八步：不满足转至第六步。

第六步：判断n+1是否大于最大迭代次数，若大于转至第八步，若不大于，对输入样本Xk，反向计算每层神经元的局部梯度δ。其中：

第七步：按下式计算权值修正量△w，并修正权值：n=n+1，转至第四步。

第八步：判断是否学完所有的训练样本，是则结束，否则转至第三步。

3 对BP神经网络的改进

在基于BP神经网络程序，根据SCPTU数据对岩土进行分类时，其内部机制非常复杂，加上土的不均匀性，其各项指标的变异性亦非常大，使计算的结果不容易收敛，本文在标准BP算法的权值更新阶段引入了动量因子，即动量BP法，使权值修正值具有一定的惯性，即令：

△wij(n)=α△wij(n-1)+ηδj(n)vi(n)

α为动量因子，通常是常数。

与标准的BP法相比，更新权值时，上式增加了因式α△wij(n-1)。它表示本次权值的更新方向和梯度不但与本次计算所得的梯度有关，还与上一次更新的方向和幅度有关。这一因式的加入，使权值的更新具有一定的惯性，且具有了一定的抗震荡能力和加快收敛的能力。

4 修正的BP神经网路对桩基承载力的预测

利用地震波静力触探技术(SCPTU)可以得到沿桩长连续的qc、fs、u、vs，以这些指标为输入，桩的承载力(Qc)为输出，经过修正的BP网络的训练，可用来预测桩的荷载-沉降曲线，与现场的静载试验结果相比较，可以验证新预测方法的有效性。

为了计算简便，假设如下：

①每层土各向同性；

②桩、土之间紧密接触，无相对位移；

③桩、土都为弹性连续介质；

根据弹性力学知识，应用叠加原理可以得到桩顶的沉降为：

(1)

其中，Qp为作用在桩顶的竖向荷载；ESi为第i层土的弹性模量；d为桩径；Iρi为位移影响因子，其表达式为：

(2)

式中，μi为第i层土的泊松比；L为桩长。

运用式(2)——进行桩基承载力的计算是以桩的极限位移为控制准则的。土的弹性模量通过土层的剪切波速Vs得到：

(3)

土层越密实，用SCPTU技术得到的剪切波速越大，在触探初期，土层处于小应变状态，测得的剪切模量最大，根据式(3)，此时弹性模量也最大。在触探过程中，土的变形亦越来越大，逐步由小变形状态过渡到大变形状态，弹性模量越来越小，因此需要对初始弹性模量进行修正，故引入了弹性模量的指数衰减公式[1]，

(4)

式中，Qu为极限荷载。

通过对各场地进行SCPTU测试，分别用修正的BP神经网络方法，静载试验方法对各个场地各土层的数据进行统计，将其弹性模量进行归一化处理，可以得到两种方法弹性模量的变化曲线如图1所示。通过图形的比较发现，弹性模量的实测值和预测值具有相同的变化趋势，且误差在允许的范围内波动，表明通过修正的BP神经网络预测出地基土的弹性模量，是可以用来进行桩基承载力的计算的。

图1 土层弹性模量的衰减曲线

为了验证桩长、桩径以及成桩方式对桩基承载力的影响，本文收集了部分江苏地区桩基静载试验数据和现场SCPTU数据，经过修正的BP神经网络预测，得到了不同情况下预测值和实测值的比较结果见图2～图8。

图2～图3为相同桩长，相同桩径，只是成桩方式(图2为预制桩，图3为钻孔灌注桩)不同的桩的预测结果与静载试验实测值的比较结果。图2与图4为不同桩长，相同桩径和成桩方式的预测结果与实测值的比较结果。

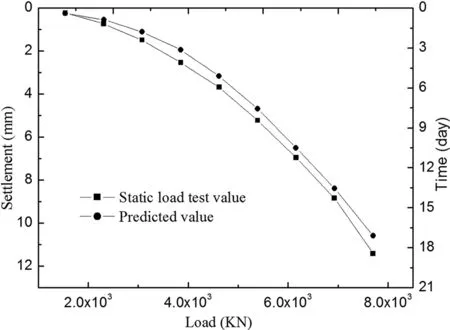
图2 预制桩的比较结果(L=45 m，d=700 mm)

图3 钻孔灌注桩的比较结果(L=45 m，d=700 mm)

图4 预制桩的比较结果(L=30 m，d=700 mm)

图5 钻孔灌注桩的比较结果(L=25 m，d=400 mm)

图6 预制桩的比较结果(L=25 m，d=400 mm)

图7 BP方法，CPT方法和静载试验方法结果比较

图8 BP方法，CPTU方法和静载试验方法的结果比较

由图2和图3的比较可以发现，用神经网络预测得到的结果比静载试验实测值要偏大，原因在于静载试验的结果反映的是在只加载21天后的沉降，而实际上，通常情况下，桩基的沉降是随着时间不断增加的，而且用预制桩预测的结果较钻孔灌注桩的结果更接近静载试验值，且小于灌注桩的预测值，原因在于预制桩的强度(C70)要高于灌注桩(C30)，桩身本身的变形较小。比较图2和图4发现，在开始加载时，桩长越短，预测值与实测值吻合的越好，但随着荷载的增大，预测值趋向大于实测值。原因在于加载初期，桩越长，对周围土的扰动越大，桩与周围土的相对位移就越大，预测值与实测值的误差亦相对较大，反之则越小。但随着荷载的继续增加，桩贯入土层的长度增大，桩顶处的扰动土对桩的影响越来越小，预测值与实测值的误差可能主要与成桩后的时间长短有关，时间越长，误差越大。

由图5和图6的比较结果来看，对于预制桩的预测效果要明显优于钻孔灌注桩的预测效果，原因可能在于预制桩的桩身材料性质比较稳定，其荷载-时间-沉降变形曲线的变异性小，比较稳定。结合与图2，图4的比较，桩越短，桩径越小，其预测的沉降结果与实测值越大，原因为桩在受到竖向荷载时，会受到周围土的相互作用，桩越短，桩径越小，周围土对桩身的束缚会相对小一些，桩身自由位移幅度越大。

图6和图7为本文方法与传统的CPT/CPTU方法以及静载试验结果的比较。

图7和图8的比较结果表明，传统的CPT/CPTU方法预测的桩基承载力要比实测值大很多，原因在于CPT/CPTU方法只是将靠近桩尖的静力触探数据经过修正作为预测桩基承载力的参考值，偏于保守，预测得到的桩基承载力较小。与实测值的最大误差相对较大。而在岩土工程领域误差在25%之内是可以接受的，因此，用CPT/CPTU方法预测得到的桩基承载力有时只能作为一种参考值，不能直接用于工程实践当中。

5 结 论

通过工程实例分析比较，验证了BP神经网络算法在预测桩基和地基承载力方面的有效性。

(1)基于BP神经网络的预测功能，可以利用SCPTU数据对桩基的承载力进行预测，可以获得精度较高的结果，同时避免了复杂的理论计算，可以在工程实际中推广应用。

(2)利用SCPTU得到的剪切波速可以获得桩周土的刚度，这样可以对地基土的变形进行控制，从而可以从应力和位移两个方面对桩基的承载力进行预测，两种方法互相参照对比，可以提高预测的精度。

(3)通过与传统原位测试方法的比较，不难看出，从现阶段的技术水平来看，利用SCPTU进行桩基承载力的预测最接近实际情况。

[1] Paul W. Mayne. Evaluating Axial Drilled Shaft Response By Seismic Cone[J]. Foundations & Ground Improvement，GSP 113，ASCE，Reston/VA，pp. 655～669.

[2] De Ruiter J，Beringen F L.Pile foundations for large North Sea structures[J]. Mar Geotechnique，1979，39(3)：267～314.

[3] Bustamante M，Gianeselli L. Pile bearing capacity prediction by means of staticpenetrometer CPT[C]. Proceedings of the second European symposium onpenetration testing，Amsterdam：Balkema，1982：493～500.

[4] Meyerhof G G. Bearing capacity and settlement of pile foundations[J]. Journal of Geotechnical Engineering，ASCE，1976，102(3)：197～228.

[5] Tumay M T，Boggess R L，Acar Y. Subsurface investigation with piezocone penetrometer[C]. Proc Cone Penetration Testing and Experience，New York：ASCE，1982：325～342.

[6] Schmertmann J H. Guidelines for cone penetration test[M]. Washington，D.C：performance and design，1978.

[8] Goh，A.T.C. Nonlinear modelling in geotechnical engineering using neural networks[J]. Australian Civil Engineering Transactions，1994，36(4)：293～297.

[9] Goh，A.T.C. Empirical design in geotechnics using neural networks[J]. Geotechnique，1995，45(4)：709～714.

[10] Goh，A.T.C. Back-propagation neural networks for modeling complex systems[J]. Artificial Intelligence in Engineering，1995，39(3)：143～151.

[11] Goh，A.T.C. Pile driving records reanalyzed using neural networks[J]. Geotech. Engrg.，ASCE. 1996，122(6)：492～495.

[12] Abu-Kiefa，M. A. General regression neural networks for driven piles in cohesionless soils[J]. Geotech. & Geoenv. Engrg，ASCE，1998，124(12)：1177～1185.

[13] Shahin，M.A.，Jaksa，M. B，and Maier，H. R. Predicting the settlement of shallow foundations on cohesionless soils using back-propagation neural networks[R]. Research Report No. R 167，2000.

[14] F. Pooya Nejad a. Prediction of pile settlement using artificial neural networks based on standard penetration test data[J]. Computers and Geotechnics，2009，36(9)：1125～1133.

[15] 蒋建平，阎长虹，高广运. 地基土压缩系数的RBF神经网络预测[J]. 江苏大学学报·自然科学版，2011，32(2)：232～235.

[16] 张丽萍. 基于小波概率神经网络的单桩竖向承载力预测模型及应用研究[J]. 工业建筑，2012，42(9)：107～110.

[17] Mohamed A. Load-settlement modeling of axially loaded steel driven piles using CPT-based recurrent neural networks[J]. Soils and Foundations，2012，117(4)：1969～2015.