某露天煤矿抛掷爆破及煤层开挖对边坡稳定性的影响

陈 寿 汪日生 郭飞高 刘建国

(葛洲坝易普力四川爆破工程有限公司)

露天矿边坡稳定性对于矿山安全高效生产影响较大，目前，主要采用极限平衡法和岩土数值模拟方法进行边坡稳定性评价[1]。随着研究的不断深入，根据不同的地质条件状况，极限平衡法可进一步分为简布法、毕肖普法、瑞典条分法、斯宾赛法、不平衡推力传递法、摩根斯坦-普拉斯法、萨尔玛法等[2-3]。在岩土工程领域常用的数值模拟方法主要有有限元极限法[4-6]、离散元法[7]、快速拉格朗日分析法[8]、边界元法[9]、块体系统不连续变形分析法[10]、数值流形方法[11]等。我国西北地区某露天煤矿在抛掷爆破和拉斗铲倒堆开挖过程中，实体高台阶曾发生多次滑坡，严重威胁着台阶上方钻机及台阶下方采煤机械和人员安全。为确保该矿安全生产，本研究采用Geo-studio和FLAC3D软件分别对爆破振动、煤层开挖因素影响下的边坡稳定性进行分析，为实体高台阶实时监控预警及滑坡快速治理提供理论依据。

1 工程概况

本研究矿区抛掷爆破的实体高台阶主要由岩层和煤层组成。煤层为主采的6#复合煤层，该煤层属于层状构造，其结构主要呈现为线理状和条带状。该煤层平均厚度为28.8 m，整体埋藏十分平缓，倾角为3°～5°，煤层硬度、韧性、密度普遍较大，脆性稍差。6#煤层以上的岩石台阶主要为黏土岩、泥岩、砂泥岩，岩层高度为38～42 m，属于坚硬—半坚硬岩石，普氏硬度系数为3.4～6.0。当前岩石台阶的设计倾角为65°，煤层边坡设计倾角为75°，岩石高台阶长约2 200 m，煤层开采工作分为东西两区，工作面长度均为1 000 m左右。本研究以东区为例，依据《煤炭工业露天矿设计规范》(GB 50197—2015)和《岩土工程勘察规范》(GB 50021—2001)，并结合该矿抛掷爆破实体高台阶的存在期较短(1～2个月)的特征，确定实体高台阶边坡的储备安全系数为1.2。根据矿区地质资料并结合现场取样，在实验室测得的煤岩体的物理力学参数见表1。

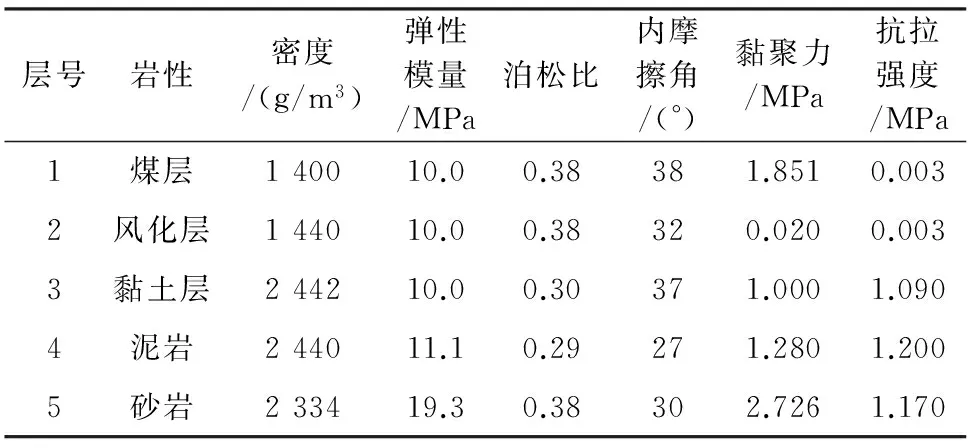
表1 矿区煤岩体物理力学参数

2 爆破振动影响下边坡稳定性分析

2.1 西区爆破振动影响分析

2.1.1 模型构建

本研究运用基于极限平衡法的Geo-studio软件中QUAKE/W动力有限元模块根据西区的实际情况构建了如图1所示的模型。模型上覆岩层台阶高44 m，坡面倾角65°，中部煤层厚28 m，坡面倾角75°，下部基岩主要为厚72 m的泥岩。整个模型基底长300 m，高144 m。

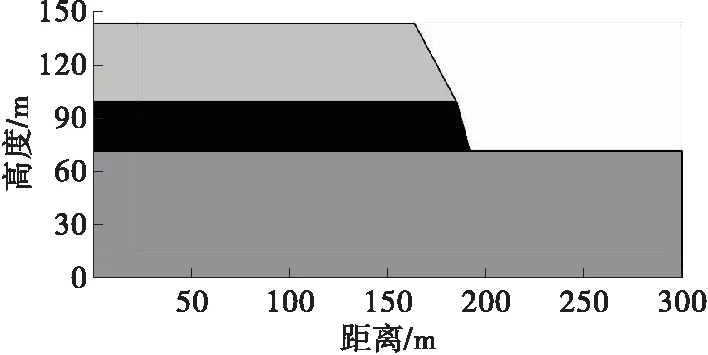
图1 台阶剖面模型

2.1.2 计算结果分析

由Geo-studio软件自带的地震波模拟现场爆破振动产生的震动波，在西区初始模型的基础上导入了历时10 s的地震波(图2)。地震波传播至边坡的瞬间，边坡向自由面发生了剧烈晃动。软件默认以0.02 s作为时间步长记录地震波对边坡的影响，故10 s的震动共计500步，按每20个时间步长保存一次记录。在初始应力模型的基础上再次添加边坡稳定性分析模块，基于摩尔-库伦理论得到的安全系数为1.15[12]，相应的安全储备系数为1.2，但无法认定边坡会一定发生破坏。

图2 振动过程中的地震波谱

受地震波的影响，边坡的安全系数变化较大，由图3(a)可知，安全系数在爆破振动过程中剧烈变化，多次降至1.0以下，因此在分析边坡受振动影响时是否会发生坍塌，应侧重于分析爆破振动过程中的边坡位移量。图3(b)显示在持续10 s的振动过程中，实体高台阶边坡受爆破振动影响产生的永久性位移量约为0.27 m，如此大的位移较易诱发边坡在原本不稳定的破坏面处发生滑坡。由此可见，爆破振动对边坡岩层的破坏较大，是影响边坡稳定性的关键因素，因此，在爆破作业后应认真确定边坡的稳定性。

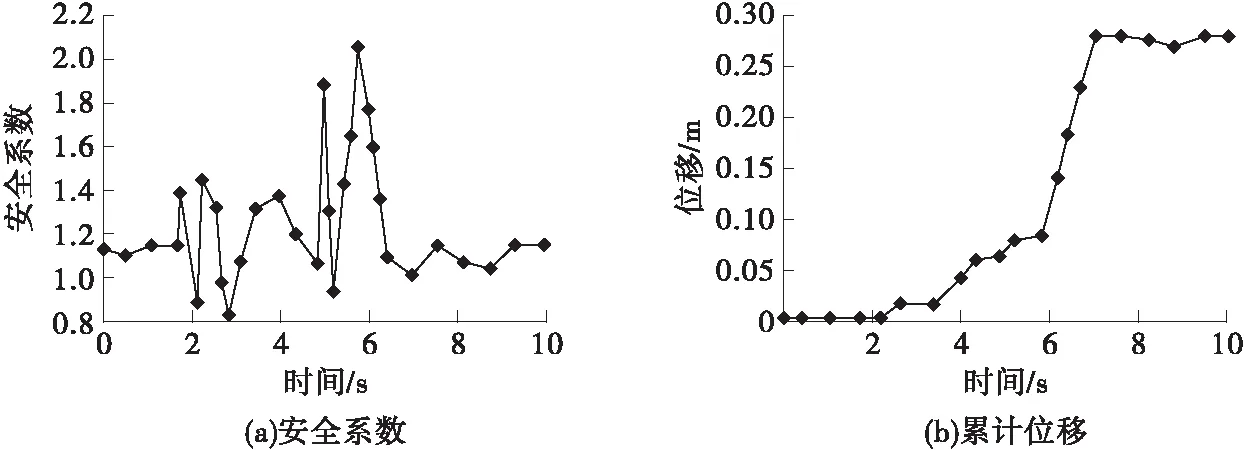
图3 爆破振动过程中安全系数及位移随时间的变化特征

2.2 不同爆破强度下的边坡稳定性

爆破设计选取的参数不同，产生的爆破振动强度也不同。为研究不同振动强度对边坡稳定性的影响，本研究设定了4组不同振动强度参数(表2)，在重力场下考虑爆破振动的影响，运用Geo-studio软件的QUAKE/W模块，采用摩根斯顿-普赖斯法分析了不同振动强度下的边坡稳定性，得到的安全系数如表2所示。

表2 振动强度参数设定

由表2可知：随着爆破振动强度增大，边坡安全系数趋于减小。数值模拟表明：质点振动加速度超过0.2 g时，边坡安全系数基本小于1.0，根据《煤炭工业露天矿设计规范》(GB 50197—2015)，安全系数小于1.0的实体高台阶边坡发生破坏的可能极大。在4种不同振动强度作用下，边坡产生的位移量如图4所示。分析图4可知：当质点的振动加速度a超过0.1 g时，位移大幅高于0.16 m；当a达到0.4 g时，产生的位移量达到1.02 m，产生的位移极大，易导致边坡产生较大裂缝，在进一步受到降雨、下方煤层开挖扰动的影响后，边坡极易发生变形破坏。可从降低炸药量、采用微差爆破、改变装药结构、设置人为减振带、控制爆破频率减少位移累积等方面采取相关措施，来降低爆破振动危害。

图4 振动过程中的边坡累计位移

3 开挖扰动下边坡稳定性分析

3.1 模型构建

仍以西区为例，运用基于数值模拟法的FLAC3D软件构建了数值模型进行边坡稳定性分析。模型剖面长250 m，采煤工作面长400 m，模型高144 m，以Z方向-72 m处为模型的底边界，沿X正方向开挖，最终形成的模型单元数为95 040个，节点数 102 060个(图5)。

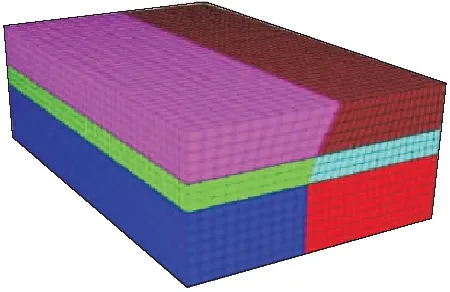
图5 三维FLAC3D计算模型

3.2 模拟结果分析

本研究采用开挖上覆岩层的方式来模拟拉斗铲倒堆作业的过程。数值模拟表明：随着岩层逐步开挖，经历不断卸载、应力释放、自由变形等一系列过程后，在坡面附近的岩体内会发生应力重新分布(图6)。分析图6可知：台阶上方位移矢量向下表现为沉降，中部位移矢量几乎与坡面平行表现为剪切，开挖位置位移矢量向上表现为剪出，开挖后坡底出现剪切破坏，但整体上边坡仍处于稳定状态。根据工作面日采煤进度以及模型尺寸，进行了开挖煤层模拟，每次开挖前进20 m，整个模型开挖分20步完成，最终最大不平衡力逐渐收敛，模型趋于平衡状态。

图6 上覆岩层开挖后塑形区分布

由于煤层开挖次数较多，故本研究选取开挖第1、10，19步进行了分析。结果表明：边坡开挖引起地应力释放，开挖周围坡体会产生卸载回弹变形，坡体向自由面移动，并且随着时间积累变形范围逐渐扩大；在坡体临空面处，尤其是坡脚位置，易形成剪应力增高区域，向坡体内部逐渐减弱；卸载过程中应力释放量最大的位置位于开挖面周围，从模型侧面来看，坡体由上至下依次呈沉降、剪切、剪出状态，整体易形成圆弧形剪切破坏。

开挖卸载使地层特别是开挖后的部分煤岩层隆起现象较明显，煤层在开挖过程中，基底岩层隆起的程度呈先增大后逐渐减小的趋势，在开挖至中间位置时隆起程度达到最大。上覆岩层开挖后，煤层隆起量达222.6 mm，煤层全部开挖完毕后，基岩隆起量为233.5 mm，本研究模拟开挖后的位移变化特征基本符合实际情况。本研究数值模拟得出的边坡安全系数为1.18，表明在开挖过程中，边坡勉强能够维持稳定状态，但经过爆破振动和开挖的复合作用后，边坡安全系数将大大降低，极易造成滑坡或大面积垮落。

4 结 语

以我国西北地区的某露天煤矿为例，针对该矿在抛掷爆破及煤层开挖过程中高台阶、大坡角边坡严重影响了矿山安全生产的实际情况，分别运用极限平衡法与数值模拟法计算出了实体高台阶在爆破振动、煤层开挖影响下的安全系数。研究表明：抛掷爆破实体高台阶边坡稳定性较为脆弱，生产过程中可通过优化边坡几何参数、爆破工艺与网络以及开挖顺序，并配以雷达监测预警系统来确保矿区安全高效作业。

[1] 郑颖人.岩土数值极限分析方法的发展与应用[J].岩石力学与工程学报，2012，31(7)：1297-1316.

[2] 王玉平，曾志强，潘树林.边坡稳定性分析方法综述[J].西华大学学报(自然科学版)，2012，31(2)：101-105.

[3] 刘汉东，贾金禄.岩土工程数值计算方法[M].郑州：黄河水利出版社，1998.

[4] 郑颖人，赵尚毅，邓楚键，等.有限元极限分析法发展及其在岩土工程中的应用[J].中国工程科学，2006，8(12)：39-62.

[5] 贾住平，郑禄璟，姚 松.极限平衡法与有限元强度折减法在露天矿边坡稳定性分析中的应用对比[J].现代矿业，2016(9)：38-41.

[6] 周瑞龙，钟 豫.FLAC软件在某露天采场边坡稳定性分析中的应用[J].现代矿业，2016(8)：46-47.

[7] 王卫华，李夕兵.离散元法及其在岩土工程中的应用综述[J].岩土工程技术，2005，19(4)：177-181.

[8] 寇晓东，周维垣，杨若琼.FLAC3D进行三峡船闸高边坡稳定分析[J].岩石力学与工程学报，2001，19(5)：630-633.

[9] 窦宝松，陈秀军.边界元法及其在岩土工程中的应用[J].水利水电技术，2013，44(10)：49-51.

[10] 黄盛铨，刘 君，孔宪京.强度折减DDA法及其在边坡稳定分析中的应用[J].岩石力学与工程学报，2008(S)：1799-1806.

[11] 张国新，赵 妍，石根华，等.模拟岩石边坡倾倒破坏的数值流形法[J].岩土工程学报，2007，29(6)：800-805.

[12] 刘 杰，李建林，王乐华，等.三种边坡安全系数计算方法对比研究[J].岩石力学与工程学报，2011(S)：2896-2903.