基于Leader-Follower编队的无人机协同跟踪地面目标制导律设计

张民，夏卫政，黄坤，陈欣

南京航空航天大学 自动化学院，南京 210016

随着近年来科技水平的不断提高，无人机(Unmanned Aerial Vehicle, UAV)从最初的目标识别、通信中继到侦查监视、灾害评估等，其应用领域得到了极大的扩展，未来的应用前景极其广阔。无人机对地面目标的自动跟踪是指无人机根据地面运动目标指示(Ground Moving Target Indication, GMTI)给出的地面目标位置、速度、航向等信息并结合无人机当前的飞行状态通过特定的跟踪算法在无干预的条件下实现对地面静止或运动目标的持续跟踪，是当前无人机的一个重要的应用方向[1-4]。相对于单架无人机，多架无人机组成编队对地面目标进行协同跟踪具有更加明显的优势：① 可以扩大单架无人机传感器的作用范围，降低丢失目标的概率；② 可以提高对目标运动状态的估计精度，在应用上可以提供更高的灵活性[5-8]。无人机协同跟踪地面目标制导律设计的主要难点在于如何使得多架无人机在自动跟踪地面目标的同时能够有效维持特定编队。另一方面，不同于旋翼无人机，在跟踪静止或低速目标时，固定翼无人机为了避免失速必须保持一定的巡航速度，因此最常用的跟踪策略是采用盘旋跟踪的方式，这种方式也称为Standoff跟踪[9-11]。同时，无论单机还是编队，Standoff跟踪方式由于需要持续盘旋，因此均存在一个明显的不足，即这种方式只适合于跟踪低速目标[12-14]，文献[12]指出，采用Standoff跟踪方式，地面目标运动速度不能超过无人机最大巡航速度的30%。

本文提出了一种新的基于Leader-Follower编队的固定翼无人机协同跟踪地面目标制导方法。首先,设计一种能够克服对所跟踪目标速度限制的新型Standoff单机跟踪制导律，用于Leader无人机对地面目标的自动跟踪；然后,设计用于多架Follower无人机的Standoff跟踪制导律和圆编队相位协同制导律，使得Follower无人机均匀分布于圆周上，并且当编队进入稳态时，Follower无人机的速度将逐渐收敛于Leader无人机对应的速度、相位角趋近于所要求的角度。仿真试验表明，本文提出的新型编队跟踪策略可以很好地跟踪不同运动状态的地面目标，并且比基于经典李雅普诺夫向量法的制导方法具有更好的性能。

1 问题描述

无人机飞行控制系统由内回路(稳定回路)和外回路(制导回路)构成，在本文中认为内回路已经设计完成，能够很好地响应外回路给出的制导指令，并且跟踪移动目标时默认无人机的速度高于目标速度。在理想情况下，执行Standoff跟踪任务的无人机应保持固定高度和转弯半径,同时围绕被跟踪对象做圆周运动，因此通常可以仅考虑固定高度上的二维制导问题。记ρ为无人机与目标的相对距离，ρ∈[0,∞);ρd为期望距离;vu为无人机速度。

考察由式(1)描述的无人机二维质点运动学模型[15-17]

(1)

(2)

在本文中，Leader无人机采用Standoff方式对地面目标进行自动跟踪，并且保持恒定的巡航速度，其在Frient-Serret坐标系[7]下的几何关系如图1所示。

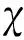
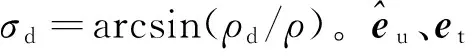
根据图1几何关系，无人机跟踪地面目标的二维模型可以表示为如式(3)所示的极坐标形式：

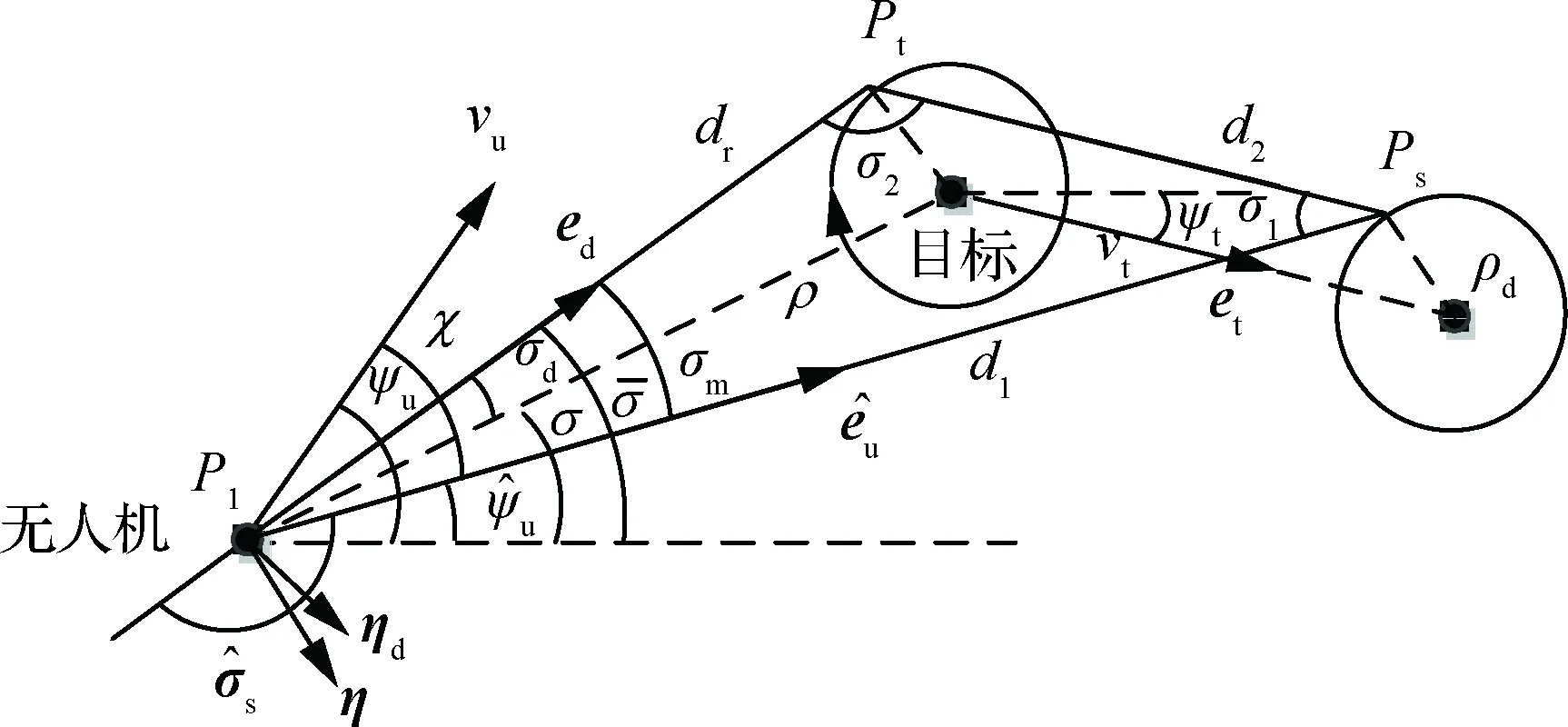
图1 无人机Standoff跟踪地面目标几何关系Fig.1 Geometry for Standoff tracking of a ground target

表1 变量定义Table 1 Definitions of variables

变量名含义定义域vu无人机速度[0,vumax]vt地面目标速度[0,vtmax]d1无人机与点Ps间的距离[0,∞)d2地面目标单位时间移动的距离[0,∞)dr无人机与切点Pt间的距离[0,∞)ρ无人机与地面目标的距离[0,∞)σ1d1与d2的夹角(-π,π]σ2dr与d2的夹角(-π,π]σddr与无人机-目标当前连线的夹角(-π,π]σ视线角(-π,π]σ切线dr与水平方向的夹角(-π,π]σmd1与dr的夹角(-π,π]^ψu无人机期望航向角(-π,π]χ当前航向与期望航向间的夹角(-π,π]P1当前无人机位置N/APt当前目标圆切点N/APsPt随地面目标移动单位时间后的位置N/A

(3)

2 Leader无人机制导律设计

当跟踪地面目标时，无人机有顺时针、逆时针2种飞行状态，为便于分析，在本文中仅采用顺时针飞行方式，逆时针方式可按同样的方法进行分析处理。

本文现提出无人机Standoff跟踪制导律：

(4)

式中:

(5)

且

(6)

针对静止目标和运动目标分别给出该制导律的稳定性分析与证明。

2.1 静止地面目标

当地面目标静止时，有vt=0，d2=0，d1=dr，σm=0，则制导律式(4)可以简化为

(7)

在式(7)中

(8)

此时式(3)所示的无人机二维模型可以简化为

(9)

定理1无人机动力学模型式(9)在制导律式(7)作用下，若满足k1>0，k2<1，则无人机跟踪静止目标的闭环系统渐近稳定。

证明:

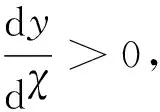
现提出李雅普诺夫方程为

(10)

对L求导可得

(11)

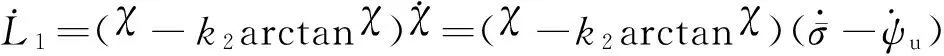
1)ρ≥ρd

由式(7)可得

再分为以下2种情况：

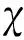
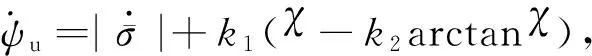
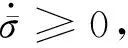
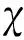
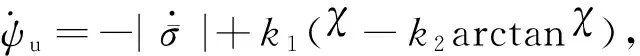
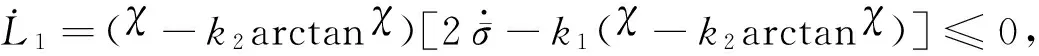
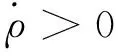
(12)

将式(12)代入式(11)可得

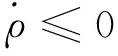
由式(7)可得

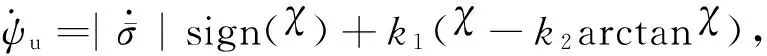
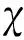
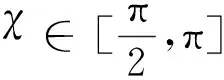
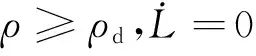
综上所述，若满足k1>0，k2<1，无人机Standoff跟踪静止地面目标时的闭环系统渐近稳定[18]。

2.2 运动地面目标

首先证明如下引理。

引理1对于式(3)所示的无人机模型，当无人机跟踪运动地面目标时，有如下不等式成立:

(13)

证明:

在图1中，显然有如下向量关系成立：

(14)

两边平方得

(15)

即

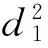
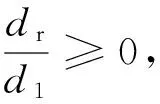
两边求导可得

(16)

(17)

将式(16)代入得

(18)

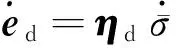
(19)

对式(19)两边同时平方，则

(20)

整理得

(21)

(22)

定理2无人机动力学模型式(3)在制导律式(4)作用下，若满足k1>0，k2<1，则跟踪运动目标时的闭环系统渐近稳定。

证明:

(23)

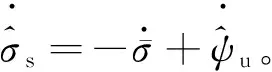
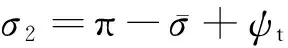
(24)

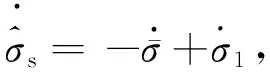
以下分3种情况分别证明。

1)ρ≥ρd

由式(4)可得

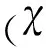
(25)

再分为如下2种情况：

①χ≥0

此时有

(26)

(27)

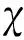
(28)

由式(4)可得

(29)

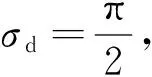
(30)

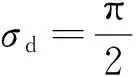
(31)

因此有

(32)

由式(4)可得

(33)

再分为如下2种情况：

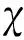
(34)

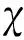
(35)

综上所述，若满足k1>0，k2<1，无人机Standoff跟踪运动地面目标时的闭环系统渐近稳定。

从上述证明过程可以看出，Leader无人机的制导律采用了一种使得无人机航向不断逼近地面目标牵连Standoff跟踪圆切线方向的策略，通过几何关系间接实现对跟踪距离的控制，从而克服了传统Standoff跟踪制导律存在的对可跟踪地面目标的速度限制问题。

3 Follower无人机制导律设计

假设在编队中有N架Follower无人机, 则第i(i=1,2,…,N) 架无人机的Dubins模型可描述为[19]

(36)

Follower无人机对Leader无人机Standoff跟踪的几何关系如图2所示(以3架Follower无人机为例)。

图2 Leader-Follower无人机编队几何模型Fig.2 Guidance geometry model of leader-follower UAVs

在本文中，多架Follower无人机需要维持一个以Leader无人机为中心的圆型编队并且均匀分布于圆周上。同时，要求Follower无人机的速度及航向角逐渐收敛于Leader无人机对应的速度及航向角，其相对运动模型可描述为

(37)

式中：下标‘0’表示Leader无人机。

同时，假设Follower无人机通过通讯链路能够获取Leader无人机的飞行状态信息，并且在Follower无人机之间具备基本的环形通讯拓扑结构。在此基础上，本文现提出如下的Follower无人机制导律。

角速度制导律：

(38)

加速度制导律：

(39)

由式(38)和式(39)可以看出，Follower无人机制导律除了对Standoff跟踪距离和编队相位角的控制外，还分别包含对Leader无人机航向角与速度偏差的控制，这是与经典Standoff协同跟踪制导律的主要差异所在。

定理3无人机编队动力学模型式(37)在制导律式(38)和式(39)作用下，若满足kω>0，kv>0，则Follower无人机与Leader无人机之间的距离将逐渐趋近于ρd，Follower无人机之间的相位差将逐渐趋近于2π/N,并且Follower无人机的速度与航向将逐渐趋近于Leader无人机的速度与航向。

证明:

现提出李雅普诺夫方程为

(40)

对式(40)求导得

(41)

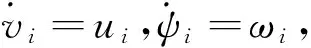
(42)

则有

(43)

4 仿真验证

为了验证本文提出的基于Leader-Follower编队的跟踪地面目标架构和制导律设计的合理性与有效性，以1架Leader无人机、3架Follower无人机组成的4机编队为例，分别针对静止目标和运动目标的跟踪问题进行仿真验证，其中在变速目标跟踪问题中不再将地面目标的速度限制在无人机巡航速度的30%以内。

在仿真开始时，无人机与地面目标的初始状态设定为：

1) Leader无人机(UAV #0)

① 位置为(0，-1 500) m；② 航向角为30°;③ 巡航速度为40 m/s；④ 制导指令输出量限幅为0.1 rad/s。

2) Follower无人机

UAV #1

① 位置为(50，-1 150) m；② 航向角为-5°；③ 巡航速度为38 m/s；④ 制导指令输出量限幅为0.1 rad/s。

UAV #2

① 位置为(-350，-1 750) m；② 航向角为120°；③ 巡航速度为41 m/s；④ 制导指令输出量限幅为0.1 rad/s。

UAV #3

① 位置为(300，-1 700) m；② 航向角为60°；③ 巡航速度为40.5 m/s；④ 制导指令输出量限幅为0.1 rad/s。

3) 地面目标

① 位置为(0，0) m；② 航向角为30°；③ 巡航速度为0～36 m/s。

制导增益设定为

k1=1，k2=0.2，kv=1.5，kω=1.28。

4.1 静止目标

无人机编队对静止目标跟踪的轨迹、速度、航向角、相位角与相对距离分别如图3～图5所示。图5(a)中Follower 2-1表示Follower 2与Follower 1间的相位角差。

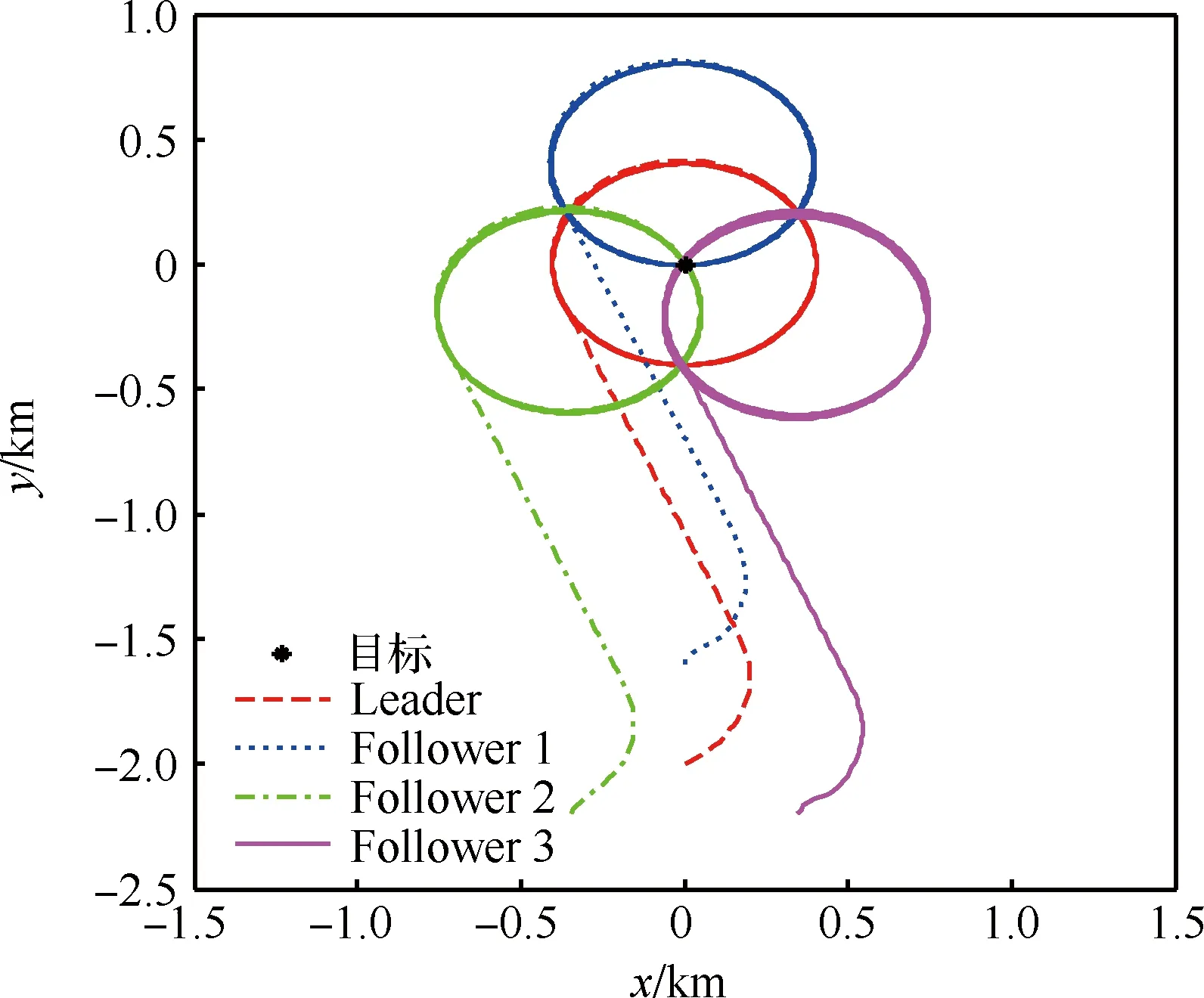
图3 协同跟踪静止目标轨迹Fig.3 Trajectory of cooperative tracking of a static target

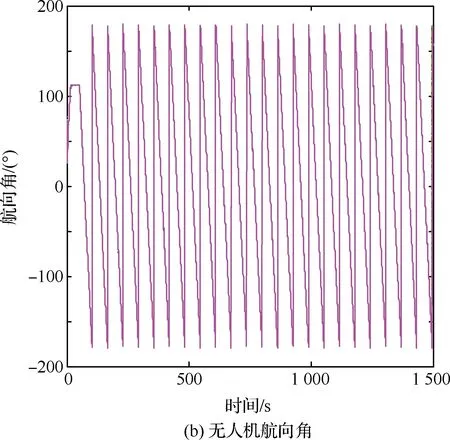
图4 协同跟踪静止目标的速度和航向角Fig.4 Speed and heading angle of cooperative tracking of a static target

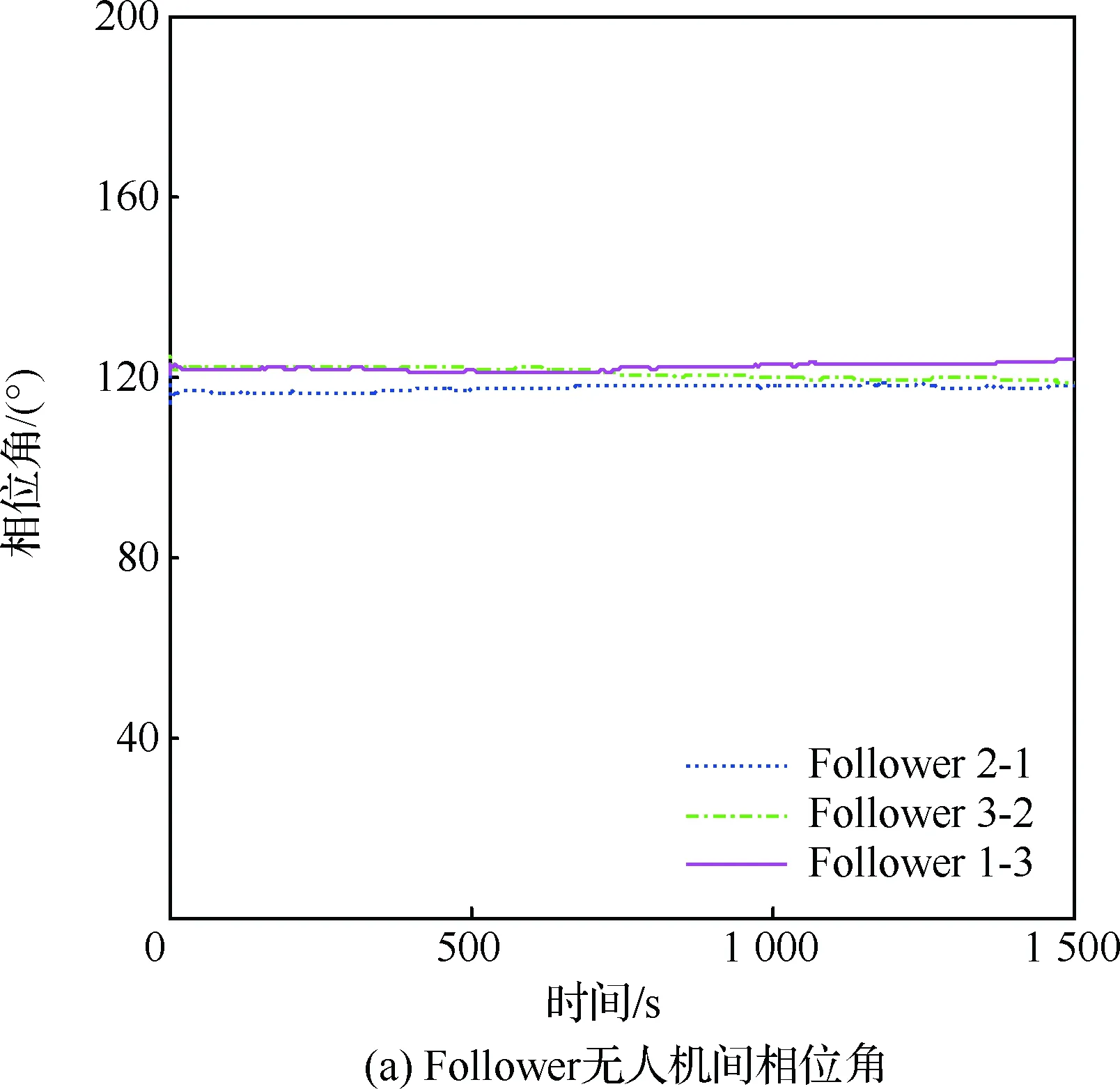
图5 协同跟踪静止目标时无人机相位角与相对距离Fig.5 Inter-UAV angle and relative range of cooperative tracking of a static target

4.2 匀速运动目标

设定以40 m/s速度巡航的无人机编队协同跟踪以36 m/s速度移动的地面目标，跟踪轨迹、速度、航向角、相位角与相对距离分别如图6～图8所示。

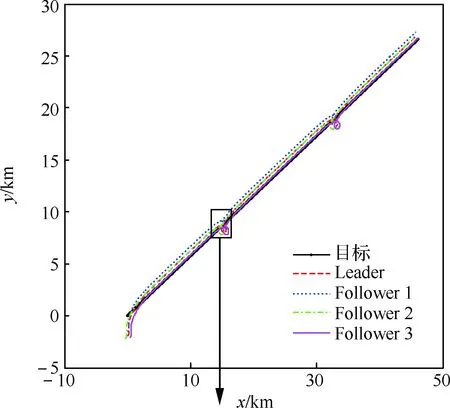
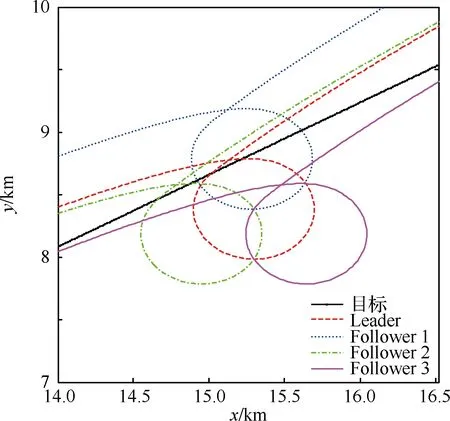
图6 协同跟踪匀速运动目标轨迹Fig.6 Trajectory of cooperative tracking of a constant speed target

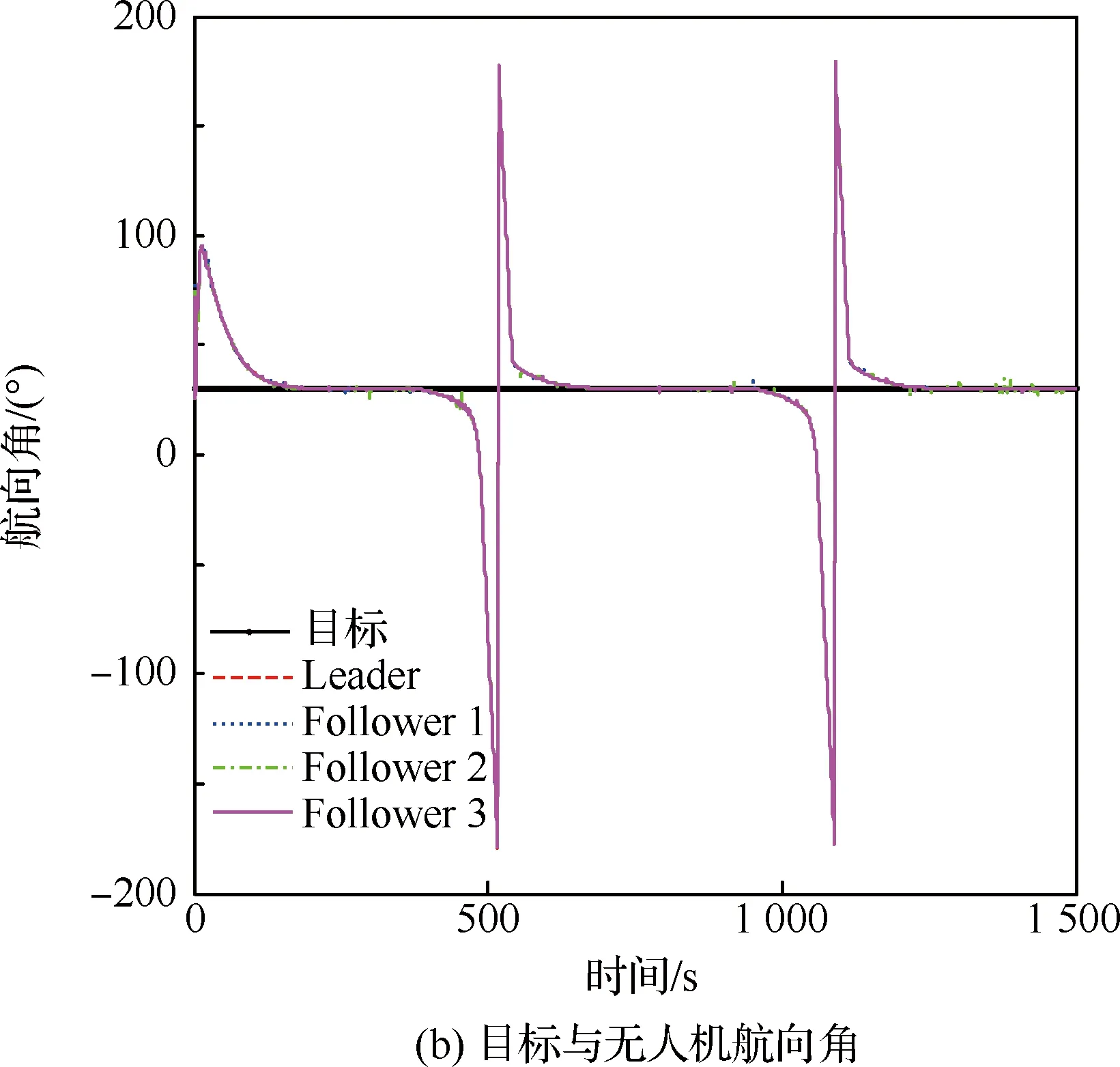
图7 协同跟踪匀速目标时无人机速度与航向角Fig.7 Speed and heading angle of cooperative tracking a constant speed target

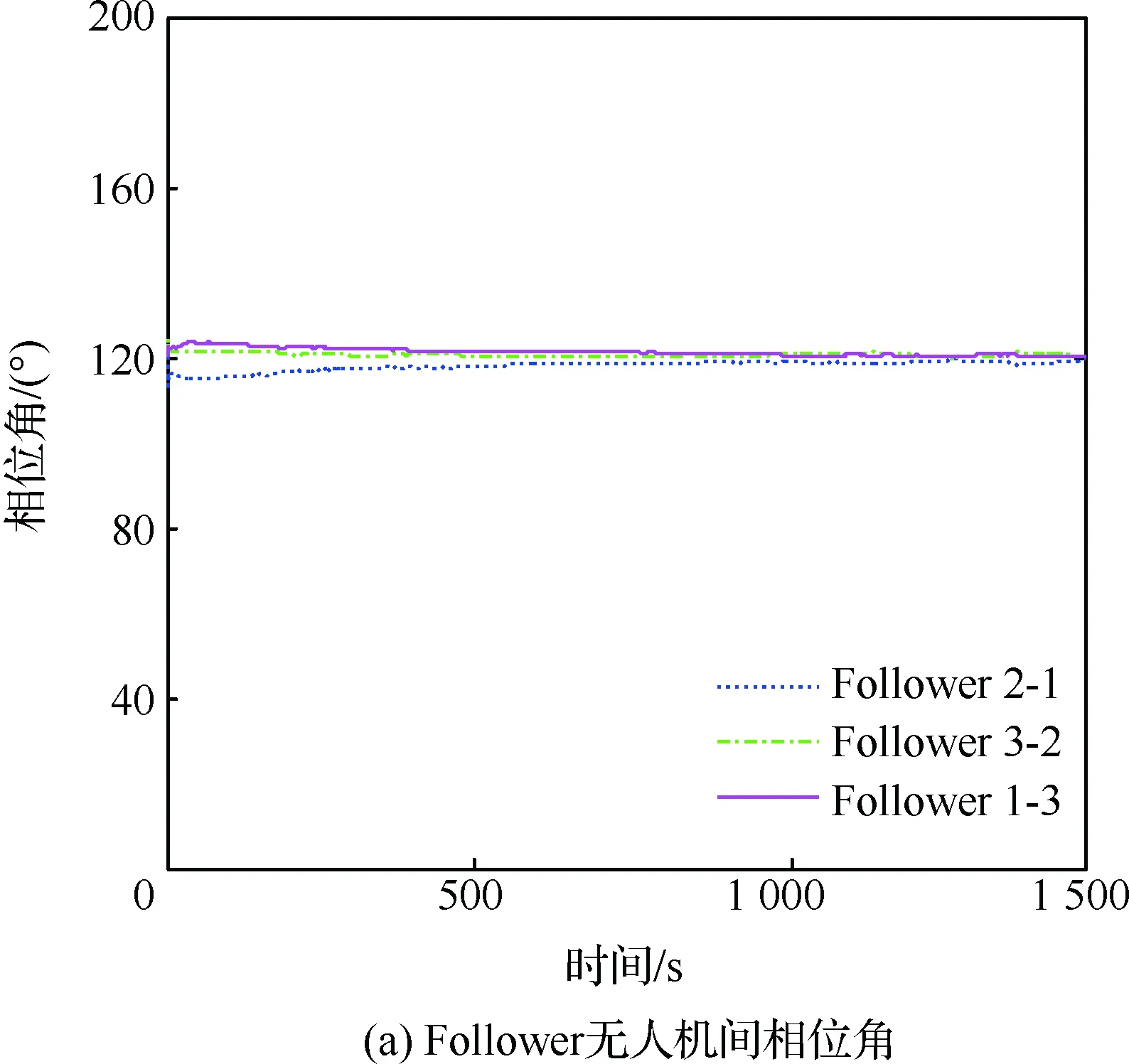
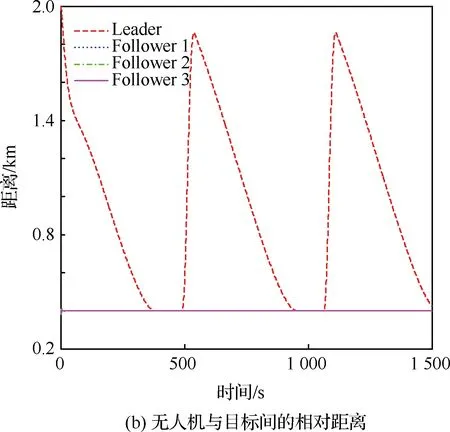
图8 协同跟踪匀速目标时无人机间相位角与相对距离Fig.8 Inter-UAV angle and relative range of cooperative tracking a constant speed target

4.3 变速运动目标

设定地面目标的速度剖面如图9所示，无人机编队对目标跟踪的轨迹、速度、航向角、相位角与相对距离分别如图10～图12所示。

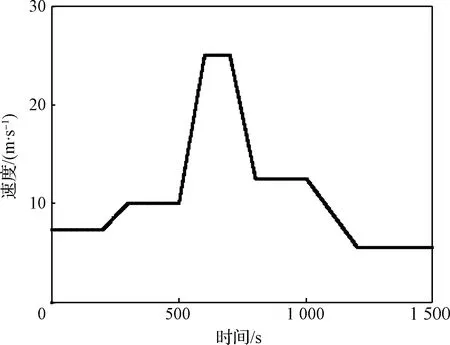
图9 地面目标速度剖面Fig.9 Profile of ground target speed

图10 协同跟踪变速目标轨迹Fig.10 Trajectory of cooperative tracking of a variable speed target

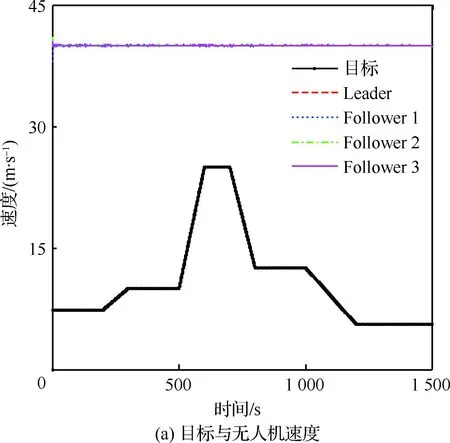
图11 协同跟踪变速目标的速度和航向角Fig.11 Speed and heading angle of cooperative tracking of a variable speed target

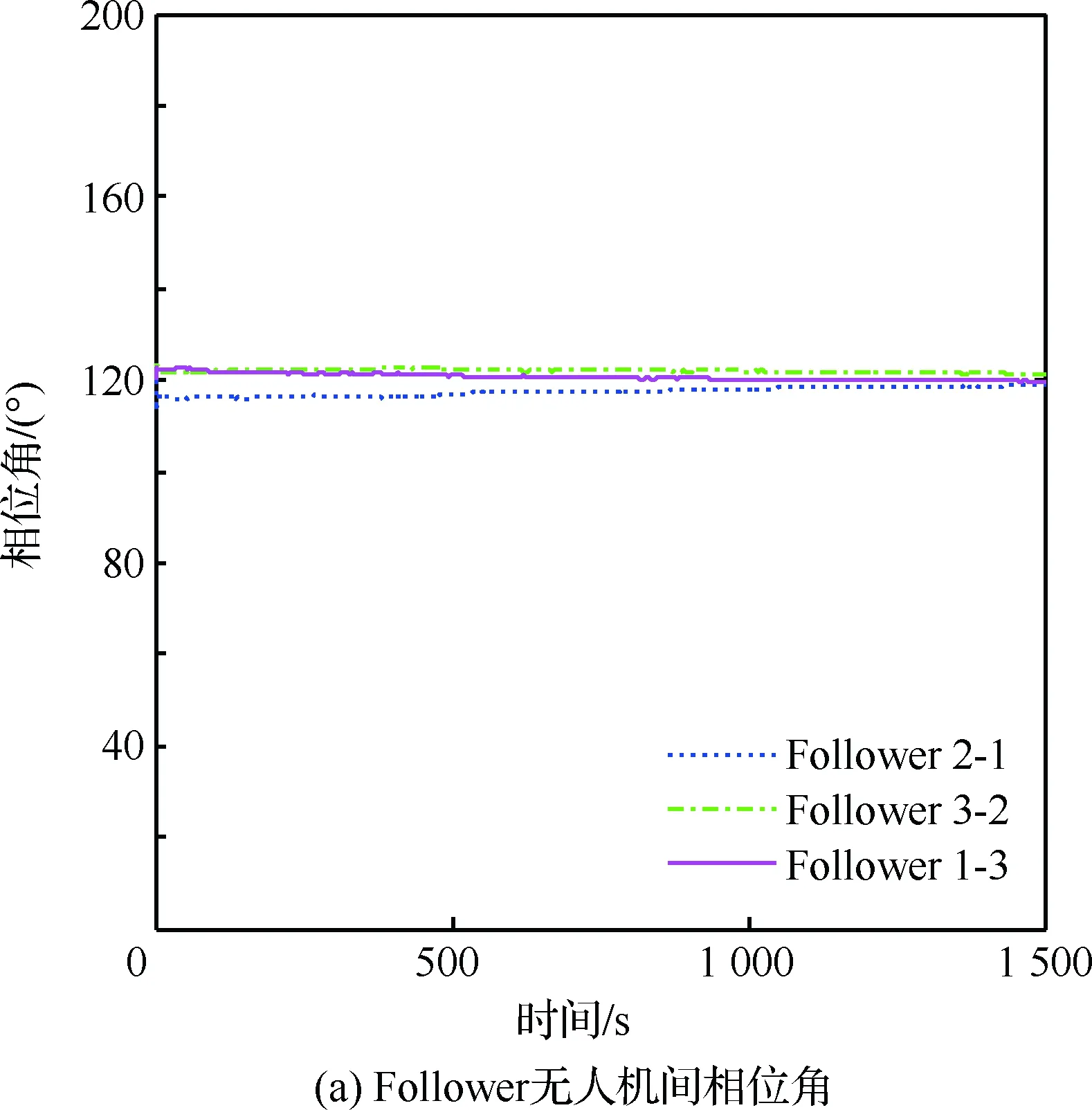
图12 协同跟踪变速目标时无人机间相位角及相对距离Fig.12 Inter-UAV angle and relative range of cooperative tracking of a variable speed target

4.4 仿真性能分析与比较

由4.1～4.3节中无人机编队对不同运动状态地面目标的跟踪结果可以看出，本文设计的无人机Leader-Follower编队架构及跟踪制导律能够很好地对包括高速运动目标在内的地面目标进行自动跟踪，同时编队与地面目标的距离以及编队内无人机间相对位置的控制完全满足设计要求。为了进一步分析本文无人机Leader-Follower编队协同跟踪地面目标的性能，选取文献[20]中的经典李雅普诺夫向量法(Lyapunov Vector Fields Guidance, LVFG)协同跟踪制导方法，在相同条件下对匀速和变速运动地面目标的跟踪问题进行了仿真。

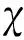
对变速运动目标的跟踪以Follower无人机中的UAV #1为比较对象，两者的速度和相位角对比结果如图14所示。

从图14可以看出，无人机协同跟踪地面目标时， 本文中的协同制导律总能使得Follower无人机的速度趋向于Leader无人机，无人机的速度与相位角的稳定性优于LVFG方法。

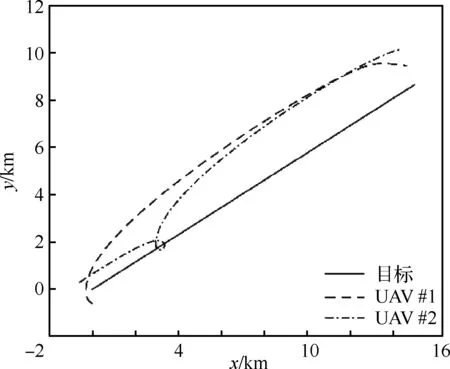
图13 采用LVFG方法跟踪高速目标轨迹Fig.13 Trajectory of tracking of a high speed target by LVFG

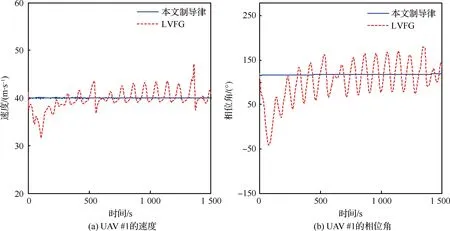
图14 2种方法得到的UAV #1速度与相位角对比Fig.14 Comparison of speed and inter-UAV angle between UAV #1 between two methods

5 结 论

本文提出了一种用于多无人机协同跟踪地面目标的新型制导方法，主要贡献为：

1) 设计了Leader无人机Standoff跟踪地面目标的制导律，解决了传统Standoff跟踪方法存在的对地面目标运动速度的限制问题。

2) 设计了Follower无人机Standoff跟踪Leader无人机的制导律，并使得Follower无人机的速度与航向角逐渐与Leader无人机的速度与航向角一致。

3) 采用李雅普诺夫直接法对所提出制导律的稳定性进行了严格数学证明。

4) 仿真表明本文提出的新型编队跟踪策略可以很好地跟踪不同运动状态的地面目标，具有工程应用价值。

[1] 陈宗基, 魏金钟, 王英勋, 等. 无人机自主控制等级及其系统结构研究[J]. 航空学报, 2011, 32(6): 1075-1083.

CHEN Z J, WEI J Z, WANG Y X, et al. UAV autonomous control levels and system structure[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1075-1083 (in Chinese).

[2] 王道波, 王寅, 蒋琬玥, 等. 基于化学反应优化的多无人机地面移动目标协同观测航迹规划[J]. 中国科学(技术科学), 2015, 45(6): 583-594.

WANG D B, WANG Y, JIANG W Y, et al. Unmanned aerial vehicles cooperative path planning for ground target tracking via chemical reaction optimization[J]. Scientia Sinica (Technologica), 2015, 45(6): 683-594 (in Chinese).

[3] RATHINAM S, ZU W K, SENGUPTA R. Vision-based monitoring of locally linear structures using an un-manned aerial vehicle[J]. Journal of Infrastructure Systems, 2008, 14(1): 52-63.

[4] LIU W, ZHENG Z, CAI K Y. Adaptive path planning for unmanned aerial vehicles based on bi-level programming and variable planning time interval[J]. Chinese Journal of Aeronautics, 2013, 26(3): 646-660.

[5] BERTUCCELLI L F, HOW J P. Search for dynamic targets with uncertain probability maps[C]∥American Control Conference. Piscataway, NJ: IEEE Press, 2006: 14-16.

[6] LI Z Y, HOVAKIMYAN N, DOBROKHODOV V, et al. Vision-based target tracking and motion estimation using a small UAV[C]∥49th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2011: 2505-2510.

[7] 齐雪, 张利军, 赵杰梅. Serret-Frenet坐标系下AUV自适应路径跟踪控制[J]. 系统科学与数学, 2016, 36(11): 1851-1864.

QI X, ZHANG L J, ZHAO J M. Advanced path tracking control of AUV in Serret-Frenet coordinate system[J]. Journal of Systems Science and Mathematical Sciences, 2016, 36 (11): 1851-1864 (in Chinese).

[8] SHAMES I, DASGUPTA S, FIDAN B, et al. Circumnavigation using distance measurements under slow drift[J]. IEEE Transactions on Automatic Control, 2012, 57(4): 889-903.

[9] YAMASAKI T, BALAKRISHNAN S N. Sliding mode based pure pursuit guidance for UAV rendezvous and chase with a cooperative aircraft[C]∥American Control Conference. Piscataway, NJ: IEEE Press, 2010: 5544-5549.

[10] MATVEEV A S, TEIMOORI, H, SAVKIN A V. The problem of target following based on range-only measurements for car-like robots[C]∥IEEE conference on decision and control and Chinese control conference. Piscataway, NJ: IEEE Press, 2009: 8537-8542.

[11] MATVEEV A S, TEIMOORI, H, SAVKIN A V. Range-only measurements based target following for wheeled mobile robots[J]. Automatica, 2011, 47(1): 177-184.

[12] SUMMERS T, AKELLA M, MEARS M. Coordinated standoff tracking of moving targets: Control laws and information architectures[J]. Journal of Guidance， Control， & Dynamics, 2013, 32(1): 56-69.

[13] VARGA M, ZUFFEREY J C, HEITZ G, et al. Evaluation of control strategies for fixed-wing drones following slow-moving ground agents[J]. Robotics and Autonomous Systems, 2015, 72(1): 285-294.

[14] CHEN B H, JIAO Z X, SHUZHI S G. Aircraft-on-ground path following control by dynamical adaptive backstepping[J]. Chinese Journal of Aeronautics, 2013, 26(3): 668-675.

[15] 吴森堂, 费玉华. 飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2005: 46-64.

WU S T, FEI Y H. Flight control system[M]. Beijing: Beihang University Press, 2005: 46-64 (in Chinese).

[16] LI Z, HOVAKIMYAN N, DOBROKHODOV V, et al. Vision-based tracking and motion estimation for moving targets using small UAVs[C]∥American Control Conference. Piscataway, NJ: IEEE Press, 2006: 1428-1433.

[17] ZHAO Q L, DONG X W, LIANG Z, et al. Distributed cooperative guidance for multiple missiles with fixed and switching communication topologies[J]. Chinese Journal of Aeronautics, 2017, 30(4): 1570-1581.

[18] KHALIL H K. Nonlinear systems[M]. 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2002: 111-174.

[19] ZHANG M, LIU H. Cooperative tracking a moving target using multiple fixed-wing UAVs[J]. Journal of Intelligent and Robotic Systems, 2016, 81(3): 505-529.

[20] FREW E W, LAWRENCE D A, STEVE M. Coordinated standoff tracking of moving targets using Lyapunov guidance vector fields[J]. Journal of Guidance， Control， & Dynamics, 2008, 31(2): 290-306.