Iterative algorithm for parabolic and hyperbolic PDEs with nonlocal boundary conditions
N.A. Al-Zaid , H.O. Bakodah
Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia
Abstract In this paper, we are concerned with the numerical solutions for the parabolic and hyperbolic partial differential equations with nonlocal boundary conditions. Thus, we presented a new iterative algorithm based on the Restarted Adomian Decomposition Method (RADM) for solving the two equations of different types involving dissimilar boundary and nonlocal conditions. The algorithm presented transforms the given nonlocal initial boundary value problem to a local Dirichlet one and then employs the RADM for the numerical treatment. Numerical comparisons were made between our proposed method and the Adomian Decomposition Method (ADM) to demonstrate the efficiency and performance of the proposed method.
Keywords: Adomian Decomposition Method; Restarted method; Parabolic and hyperbolic PDEs; Nonlocal boundary conditions.
1.Introduction
Many problems in science and engineering tend to be modelled as nonlocal mathematical problems as a result of viscoelastic behaviour of material or previous data. In particular, many branches of ocean engineering like the marine geology, geophysics, oceanography and acoustical engineering among others make use of nonlocal mathematical problems while modelling and design of various oceanographic devices and instruments. Additionally, it is sometimes better to impose nonlocal conditions since the measurements needed by a nonlocal condition may be more precise than the measurement given by a local condition, see [1-4] . Nonlocal problems are problems with presence of an integral term in a boundary condition which greatly complicate the application of standard numerical techniques like the finite difference, finite elements and spectral methods to mention a few. However, it is therefore important to be able to convert a nonlocal boundary value problem to a more desirable form of practical interest where several methods can be employed. For instance, the spectral collocation [5] with preconditioning and the radial basis functions collocation methods[6] were applied to solve nonlocal parabolic partial differential equations (PDEs) with Neumann and nonlocal boundary conditions. The Adomian's decomposition method for nonlocal heat problem and a class of hyperbolic equations with Dirichlet and nonlocal boundary conditions were treated in[4,7,8] based on the Beilin's transformation [9] . The solution of the one-dimensional nonlocal hyperbolic equation is presented using the method of lines in [10,11] , the He's homotopy perturbation method was employed for solving the initial-boundary value problem with Dirichlet and integral condition for the wave equation [12] and lastly problems with the combined Neumann and integral conditions were considered by Dehghan [13] using new finite difference schemes and Bouziani [14] , respectively.
However, in this paper, an iterative algorithm based on the RADM [15,16] of ADM for solving parabolic and hyperbolic PDES with nonlocal boundary conditions of different kinds will be proposed. ADM is a very powerful semi-analytical method with rich literature that has undergone several modifications and improvements, see [17-22,24-26] while the RADM is an algorithm that improves the accuracy of ADM and gives better approximations. In the process of computation, all calculations will be performed using the Maple software package. The structure of this paper is as follows:In Section 2 , we present the nonlocal systems of interest while Section 3 presents the standard Adomian decomposition method. In Section 4 , we give the proposed method based on the Restarted Adomian Decomposition Method.Section 5 presents the application of the proposed method and Section 6 gives a brief conclusion.
2.The nonlocal systems
In this section, we give the general forms of the parabolic and hyperbolic systems subject to initial and certain nonlocal boundary conditions together with some lemmas in each case for transforming the each system to a handable local problem.
2.1. Nonlocal parabolic System
Consider the general parabolic partial differential equation

with the initial condition

and the Dirichlet (or Neumann) with nonlocal inhomogeneous boundary conditions of the integral type

Lemma 1.ThenonlocalparabolicsystemgiveninEqs.(2.1)-(2.3)reducestoalocalsystemoftheform

where,

Proof.The proof follows immediately after setting

2.2. Nonlocal hyperbolic System
Consider the general hyperbolic partial differential equation

subject to the initial conditions

and the Dirichlet (or Neumann) with nonlocal inhomogeneous boundary conditions of the integral type given in (2.3) ; whereg(x,t) is a source function,Nu(x,t) is a nonlinear term.
Lemma 2.ThenonlocalhyperbolicsystemgiveninEq.(2.7)and(2.8)and(2.3)reducestoalocalsystemoftheform

where,

Remark 1.The proof follows as in above.
3.Standard Adomian Decomposition Method
This section presents the method of solution of the above two problems using the standard Adomian Decomposition Method (ADM) as follows:
3.1. ADM for the nonlocal parabolic system
Rewriting the PDE in the system given in Eq. (2.4) in an operator form, we get:

whereLtx=vtxandRv= -r(x,t)vx-s(x,t)vxx+p(x,t)vxxx. We define two inverse linear operators as

Applying these operators to Eq. (3.1) alongside taking into account the initial and boundary conditions in Eq. (2.4) ; we obtain

respectively. On averaging Eq. (3.4) and (3.5) , we obtain

Therefore, the ADM offers the solution ofv(x,t) by an infinite series of components and the nonlinearF(v) by a series of polynomials given by

respectively; andAnis calculated from

Thus, substituting Eq. (3.7) into Eq. (3.6) ; ADM gives the solution of Eq. (2.4) recursively as follows:Note that, the original functionu(x,t) can be obtained on using Eq. (2.6) .

3.2. ADM for the nonlocal hyperbolic system
Considering the PDE in the system given in Eq. (2.9) with two inverse linear operators defined by

we proceed as in the above and taking into account the initial and second boundary conditions in Eq. (2.9) ; we get the solution in a recursive manner as follows:

4.Restarted Adomian Decomposition Method

Restarted Adomian Decomposition Method (RADM) was introduced Babolian and Javadi [15] to facilitate the rate of convergence of ADM and successfully used by Babolian et al.[16] and Vahidi et al. [23] which turned out remarkable numerical solution. Thus, we present this novel idea for our problems under consideration and also give algorithms in each case as follows:
4.1. RADM for the parabolic system
RADM first introduced a fixed term say ω that starts or rather facilitates the rate of convergence. Now, consider Eq. (3.6) and then add a fixed term say ω to both sides and proceed as in ADM. The RADM associates the ω tov0and then carefully selectv1and the remaining follow recursively as given below:


4.2. RADM for the hyperbolic system
Here also we present as in above, the RADM scheme for the hyperbolic system in Eq. (2.9) the following:


Also, for the algorithm, one follows similar procedure as in above.
5.Application and results
In this section, we demonstrate the efficiency proposed schemes by studying some test problems of parabolic and hyperbolic systems drawn from literature.
5.1. Example one
Consider the nonlocal inhomogeneous parabolic linear PDE


Table 1 Absolute errors comparisons for Example one.
Therefore,

Thus, for the original functionu(x,t); Eq. (2.6) gives

The RADMgives the solution of Eq. (5.4) by employing the ADM to calculatev0,v1,v2, . . . ,vn. Thus, form= 3 , we obtain the following:

5.2. Example two
Consider the nonlocal homogeneous nonlinear parabolic PDE


Fig. 1. Exact and approximate solutions comparisons for Example one.
subject to the initial condition

with Dirichlet and nonlocal boundary conditions
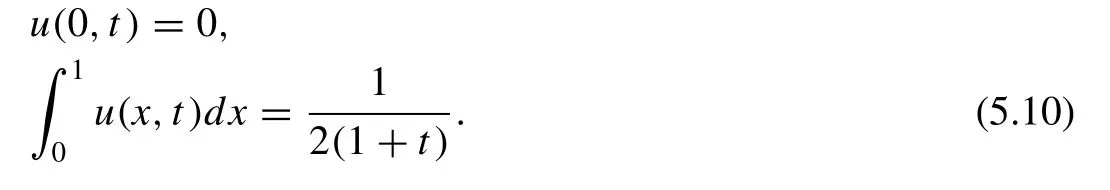
As in above, Lemma 1 converts Eq. (5.8) with conditions in Eq. (5.9) and (5.10) to a system of the form given in Eq. (2.4) and (2.5) . Thus, the ADM offers the following recursive terms:


Set ω2=v0 +v1 +v2 , thenv0 = ω2, and proceed as in above to obtainu(x,t).
The absolutes errors for the RADM and ADM att= 0. 5 and 0 ≤x≤ 1 is given in Table 2 and Fig. 2 , respectively.
5.3. Example three
Consider the nonlocal homogeneous hyperbolic linear PDE


Fig. 2. Exact and approximate solutions comparisons for Example two.

Table 2 Absolute errors comparisons for Example two.
subject to the initial conditions

with Dirichlet and nonlocal boundary conditions

Thus, Lemma 2 converts Eq. (5.13) with condition in Eq. (5.14) and (5.15) to the following system:



Fig. 3. Exact and approximate solutions comparisons for Example three.

Table 3 Absolute errors comparisons for Example three.

Set ω2=v0+v1+v2, thenv0= ω2, and proceed as in above to obtainu(x,t).
The absolutes errors for the RADM and ADM att= 0. 5 and 0 ≤x≤ 1 is given in Table 3 and Fig. 3 , respectively.
5.4. Example four
Consider the nonlocal homogeneous hyperbolic linear PDE


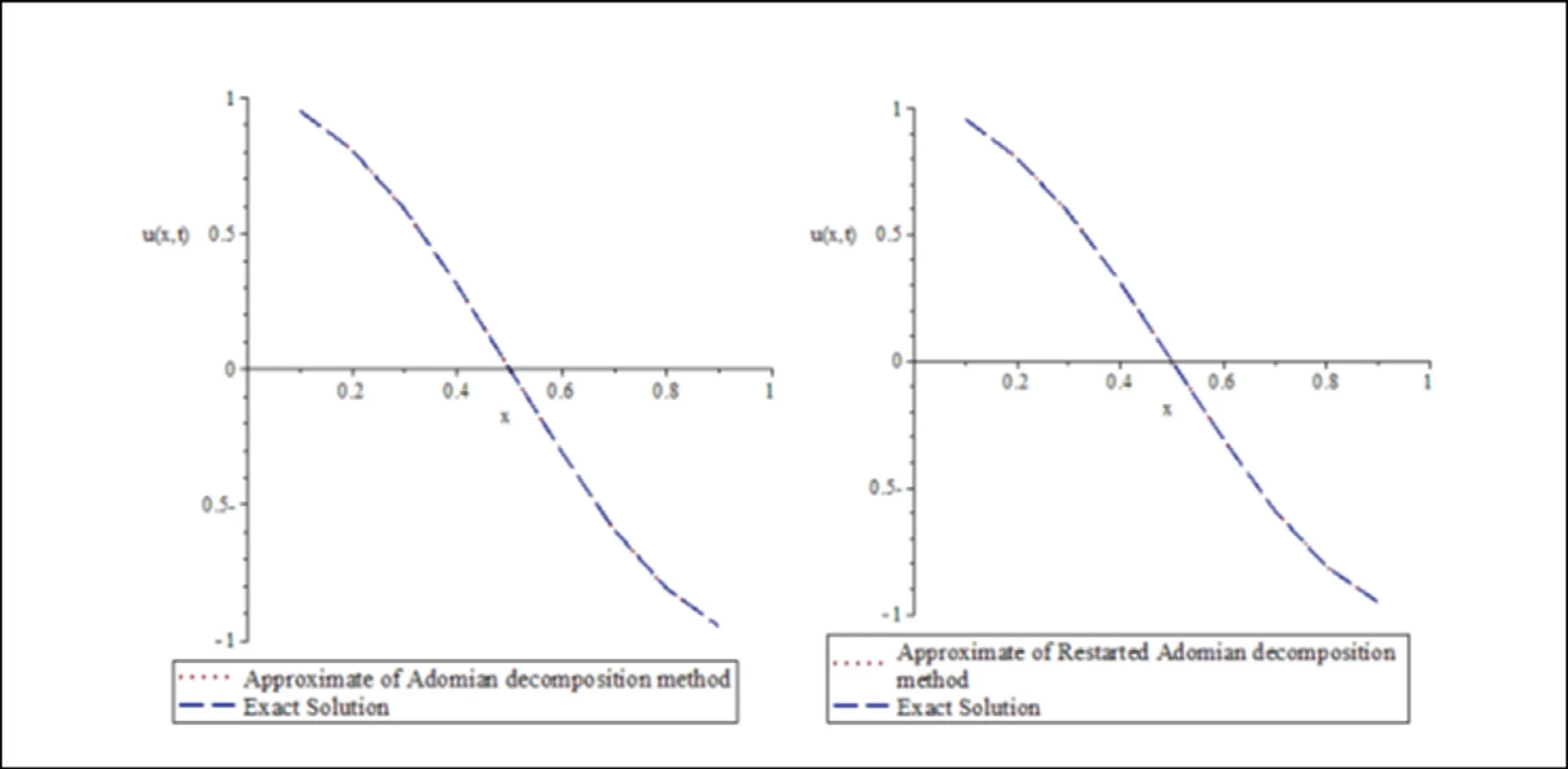
Fig. 4. Exact and approximate solutions comparisons for Example four.

Table 4 Absolute errors comparisons for Example four.

Set ω2=v0+v1+v2, thenv0= ω2, and proceed as in above to obtainu(x,t).
The absolutes errors for the RADM and ADM att= 0. 5 and 0 ≤x≤ 1 is given in Table 4 and Fig. 4 , respectively.
5.5. Example five
Consider the nonlocal inhomogeneous hyperbolic nonlinear PDE

subject to the initial conditions

It is obvious that the self-canceling “noise”terms appear between various components. Keeping the remaining noncanceled terms leads immediately to the solutionv(x,t) =x.Therefore, the original functionu(x,t) = 1 .
The RADM solution also givesv(x,t) =xwhich returnsu(x,t) = 1 .
6.Conclusion
In conclusion, we present a new iterative algorithm based on the Restarted Adomian Decomposition Method for solving nonlocal parabolic and hyperbolic partial differential equations involving dissimilar (Dirichlet or Neumann) boundary conditions including the nonlocal ones. The presented algorithm is then applied to solve effectively a large class of linear and nonlinear parabolic and hyperbolic equations and yields better solutions of high accuracy. Numerical comparisons are also established between the proposed method and the standard Adomian Decomposition Method to assess the efficiency and performance of the proposed method with the help of Maple software. Thus, the presented method is reliable and can be applied to many complicated linear and nonlinear PDEs.
 Journal of Ocean Engineering and Science2018年4期
Journal of Ocean Engineering and Science2018年4期
- Journal of Ocean Engineering and Science的其它文章
- Development of current-induced scour beneath elevated subsea pipelines
- Optimization approach for a climbing robot with target tracking in WSNs
- The effect of gravity and inclined load in micropolar thermoelastic medium possessing cubic symmetry under G-N theory
- New analytic solutions of the space-time fractional Broer-Kaup and approximate long water wave equations
- Efficient numerical scheme based on the method of lines for the shallow water equations
- Comparing the force due to the Lennard-Jones potential and the Coulomb force in the SPH Method
