一种基于GA-BP的高压混合输电线路故障分类方法
陈柏元,张红民,罗永涛,沈 洁
(1.重庆理工大学 电气与电子工程学院, 重庆 400054;2.中国电力科学研究院, 北京 100192)
电力系统输电线路主要配备架空(overhead,OH)线路。然而,随着大容量传输功率的交联聚乙烯电缆应用于实际,OH线和地下(underground,UG)电缆相结合的混合电力传输线路得到长足的发展。在人口众多的城市地区,由于建设需要和安全考虑,适合采用混合输电线路。为解决电能的传输利用问题,海上风力发电时采用水下电缆和架空线的混合输电线路也能很好地满足需要。但是混合输电线路发生故障后,需要及时检测、分类,为在规定时间内快速切除故障提供依据,从而保证电能传输连续性,恢复电力设备的正常运行,这对于保障电力系统的安全性和经济性具有重要的意义[1]。因此,对OH线和UG电缆混合线路运行状态的研究,尤其是故障状态的研究具有十分重要的理论和现实作用。
多年来,国内外专家学者对高压输电线路故障定位和识别的研究成果斐然。文献[2]利用原子能量熵和连续字符串匹配研究了配电线路故障时的故障分类。文献[3]提出了一种故障分类系统,该系统配合使用蚁群算法与模糊神经网络两大人工智能算法处理配电网故障。文献[4]完成了基于离散小波变换和支持向量机的架空线和地下电缆组成的混合输电线路中的故障定位研究。文献[5-9]探讨了输电线路发生故障时的定位和测距技术。文献分析表明:针对独立OH线的故障分类及定位研究较多,而针对混合输电线路的故障分类研究相对较少。
基于此,本文提出了一种采用OH线和UG电缆的混合输电线路搭建的模型,运用基于遗传反向传播神经网络[10](GA-BP)优化的高压混合输电线快速故障分类算法加快网络的收敛过程,进而减少训练次数,提高分类的准确率。
1 混合输电线路模型
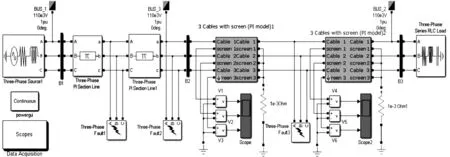
OH线和UG电缆混合输电线路的模型如图1所示。整个线路模型主要由电源、OH线、UG电缆和负载4部分组成。分别在OH线路部分、UG电缆部分及其连接处模拟不同种类的不对称短路故障的发生。

图1 混合输电线路模型
2 遗传算法优化BP神经网络
2.1 BP神经网络原理
BP神经网络模拟人类大脑内部神经网络的真实工作机制,完成信号前向和误差反向的双向流动。图2为神经网络的大体结构,其中:Xi(i=1,2,…,N)为输入数据;Ok(k=1,2,…,L)为输出数据;Wij、Wjk为连接权值;θ、α分别是隐含层和输出层的阈值。按照误差大小改变网络两层神经元之间连接权值和每个神经元计算阈值,使得网络的输出结果趋于达到既定目标[11]。大量实践表明:3层结构的BP神经网络已经能够满足实际运用的需要,即在应用时将输入层、隐含层和输出层各设置为1层。
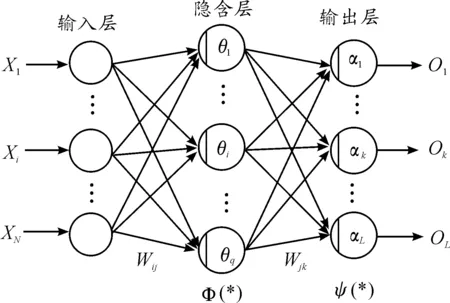
图2 神经网络基本结构
隐含层的神经元个数的取值是决定整个神经网络精度的重要因素之一。取值过大会增加整个网络结构的复杂性,导致训练耗时长,网络易过拟合;取值太小,为保证精度要投入更多的训练次数。为克服盲目取值,根据式(1)~(3)得出需要的中间层节点数可能取值。
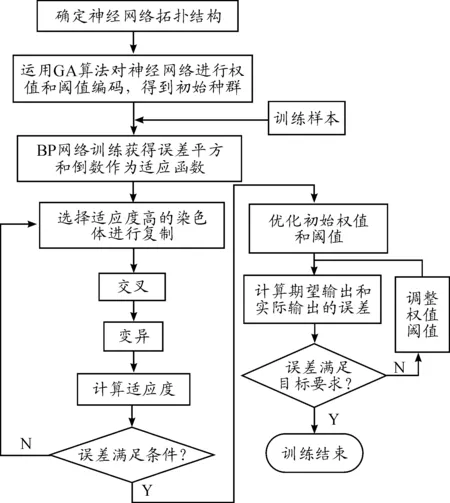
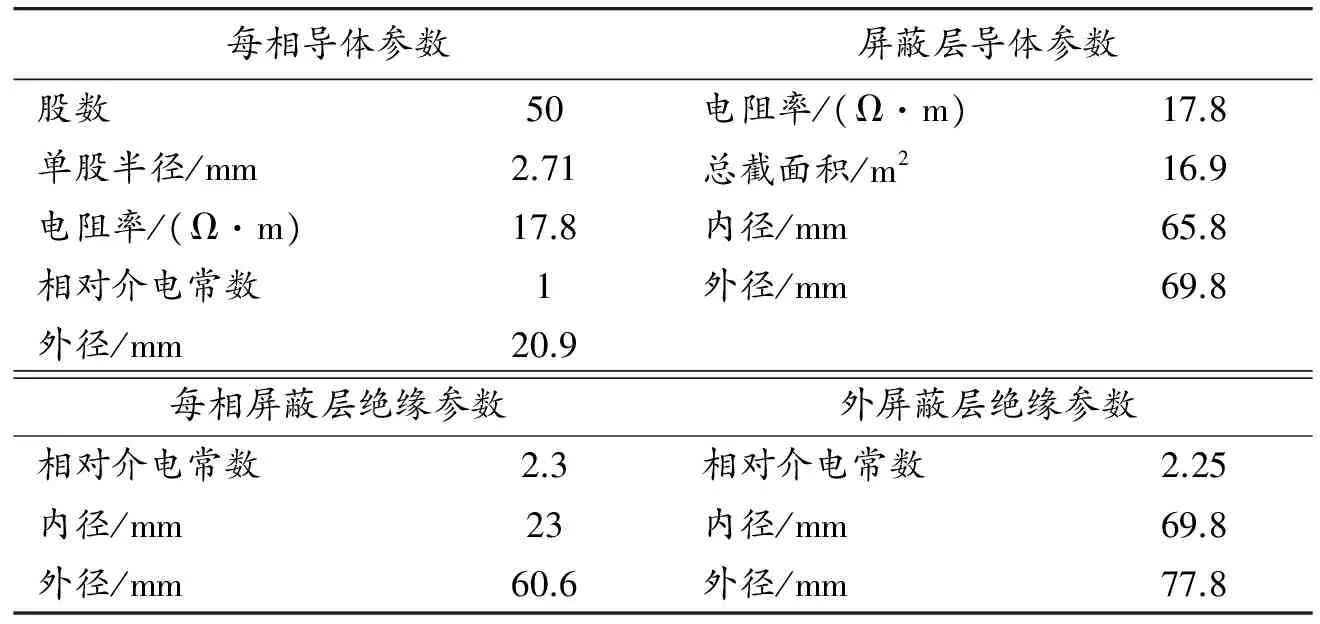
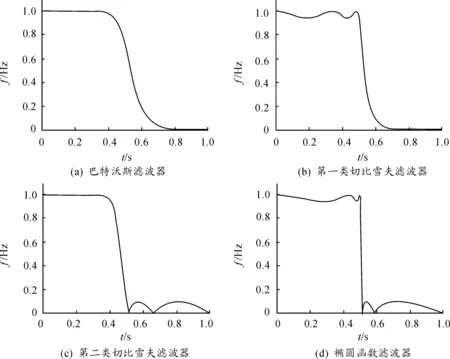
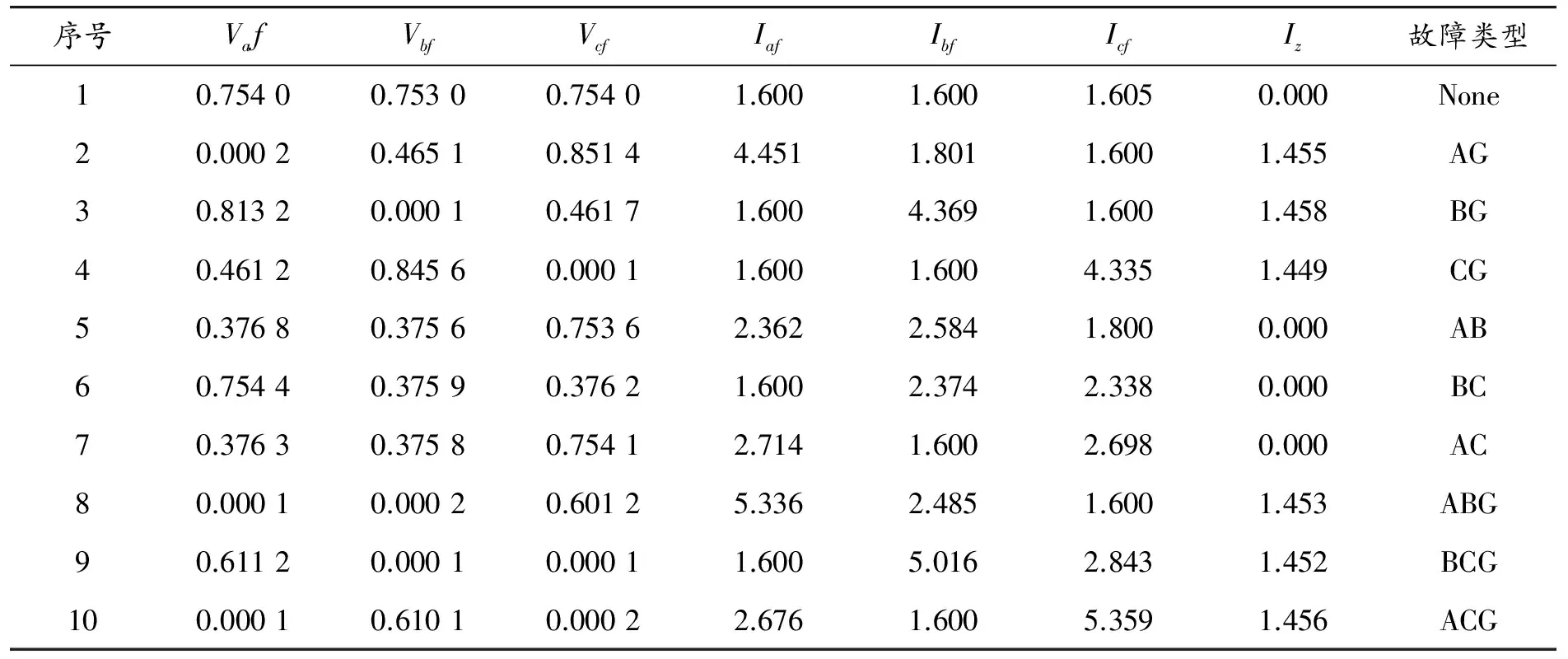
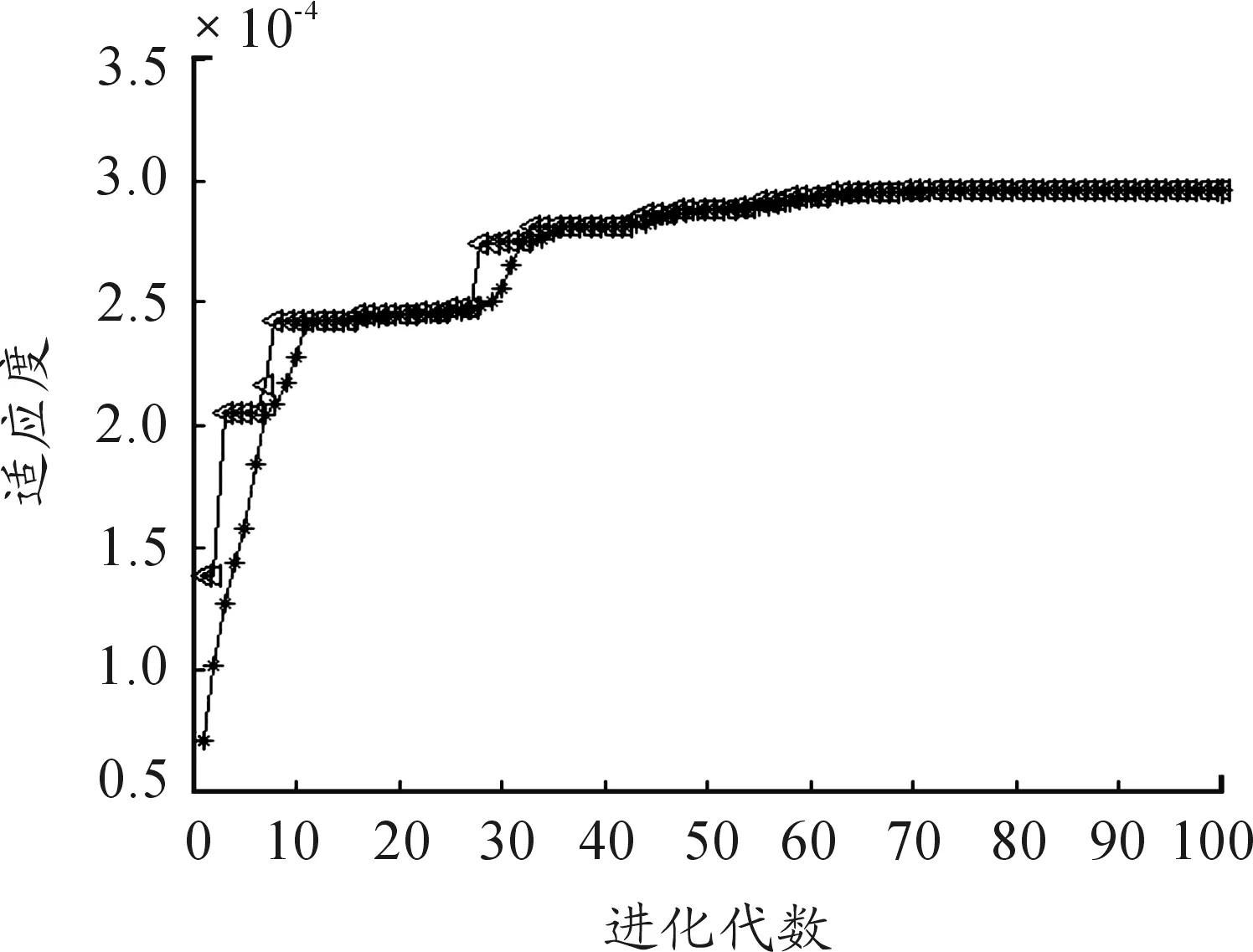
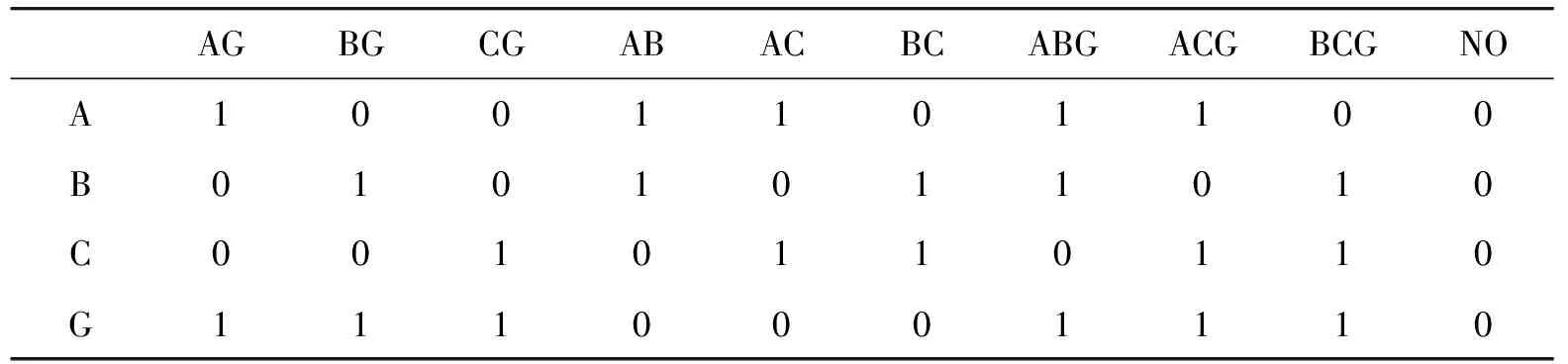
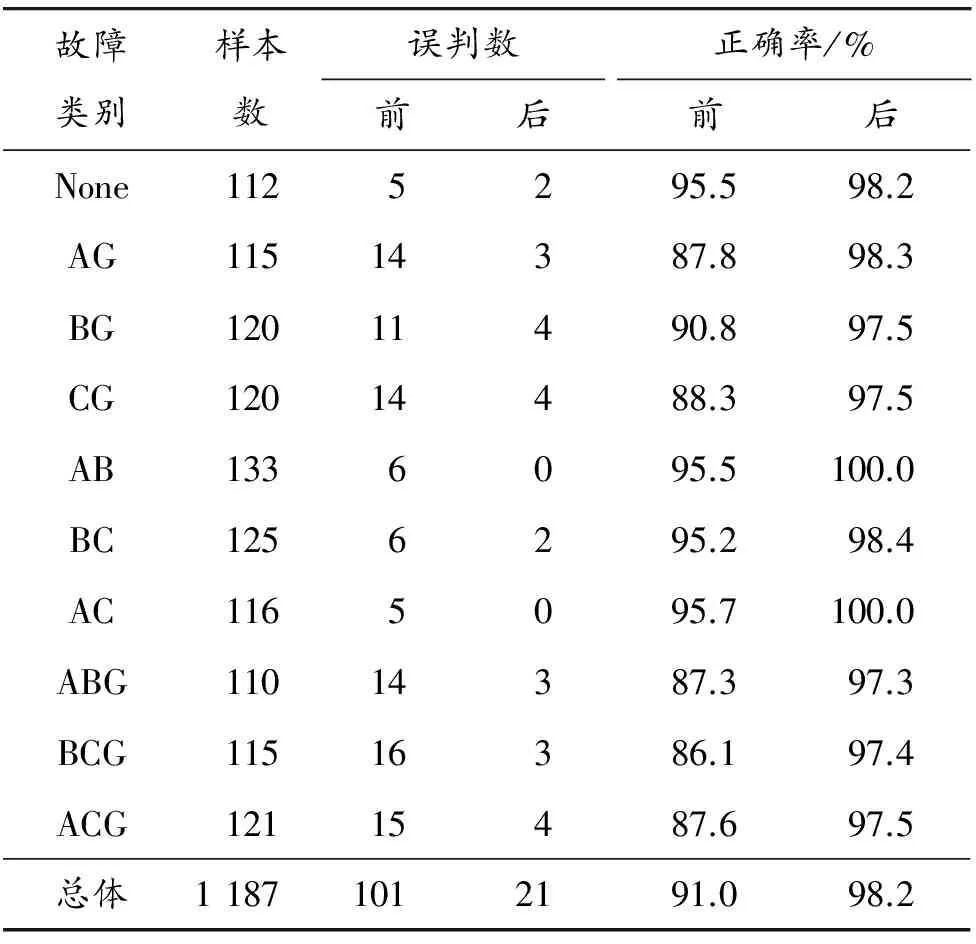
l (1) (2) l (3) 式中:n、l、m分别表示输入层、隐含层和输出层神经元数量;a为整数,a∈[1,10]。通过2个步骤得出最优个数:① 根据式(1)~(3)粗略计算取值的大致约束范围;② 采用试凑法逐个试验得出便利网络输出效果最优的唯一取值。 图3 GA-BP网络流程 遗传算法并行性好、性能稳健、搜索能力强,适用于全局问题求解,不要求多余辅助知识,无可微、连续等要求。采用神经网络结合遗传算法旨在防止网络训练过程中发生局部最优,训练中止,无法满足解决实际问题的性能要求。一般情况下,网络的初始状态值不预设,由系统随机产生,容易造成BP网络振荡甚至出现局部收敛或者不收敛情况。遗传算法可高效获得全局最优解的优势正好填补了BP网络的性能洼地,解决了初始权值、阈值不确定性带来的问题,其具体操作步骤如图3所示。算法的具体描述如下: 步骤1 初始化网络,根据故障数据类型和输入、输出数据个数设计网络的拓扑结构,确定遗传算法参数,借助GA算法编码优化对象,产生初始遗传种群。 遗传算法编码的二进制编码形式虽然便于进行遗传操作,但是不符合权值和阈值可以为任意实数的特性,这里采取实数编码方式[12]以提高遗传算法精度。编码的长度是所有待确定初始权值和阈值总数,为7×12+12×4+12+4=148个。 步骤2 输入训练样本训练BP神经网络得到均方误差。GA算法的适应度函数取误差平方和的倒数: (4) 式中:ti和Ai为网络输出的期望和实际值;m为输出神经元的所取个数。 步骤3 采用比例法选择适应度高的已编码权值和阈值进行复制,选择的原则依据式(5);而后对选取的权值和阈值进行个体之间的交叉和个体自身的变异,由此产生新种群,并计算适应度值。 若给定遗传种群大小为n,总体可表示为集合G={X1,X2,…,Xn},则个体被选择的概率Pj与个体适应度值F(Xj)之间的关系可以表述为 (5) 步骤4 重复步骤3的过程,直至误差符合目标要求,得出最佳输出的编码个体,优化过程结束。 针对实际输电线路运行过程中可能出现的单相接地短路故障(AG、BG、CG),两相短路故障(AB、BC、AC),两相接地短路故障(ABG、BCG、ACG)进行系统建模。使用Matlab R2014a建立混合输电线路模型,总长度设为23 km,包括15 km OH线和8 kmUG电缆,电源电压为110 kV,短路容量为1 500 MVA,X/R比为10,线路末端为三相串联RLC负载,系统频率为50 Hz。电缆采用接地电阻率为100 Ω·m的3芯屏蔽电缆,电缆参数配置如表1所示。架空线采用三相型等值电路,架空线的正序参数和零序参数分别为r1=0.3341Ω/km,l1=1.296×10-3H/km,c1=0.005 03×10-6F/km,r0=0.475 6 Ω/km,l0=0.504 8×10-3H/km,c0=0.008 372×10-6F/km。构建整个仿真电路模型,如图4所示。 表1 电缆参数配置 图4 混合输电线路仿真电路模型 保持架空线和地下电缆线路的各项基本参数和长度不变,模拟所有不对称线路故障。设置不同故障开始时间(FIT),故障电阻(FR)以及混合线路的不同位置(包括电缆线上、架空线上及其连接处)和不同的故障类型。巴特沃斯滤波器具有良好的通频带频率响应特性曲线,无起伏,且在通频带以外部分频率逐渐下降为零,其优越的性能相比第一类和第二类切比雪夫滤波器及椭圆函数滤波器更加适合电压和电流数据的处理。频率响应曲线如图5所示,因此采用截止频率为400 Hz的巴特沃斯滤波器处理从发送端获取的电压和电流数据,然后通过1 kHz采样频率的DFT模块获得基波值。同时,通过 Sequence Analyzer序分量分析工具获得零序电流。引入零序电流作为故障数据的一个特征量,输入网络成为一个输入分量可以提高故障数据识别的有效性和正确率。这是因为零序电流的产生必须满足3个条件:系统的中性点接地;当系统出现不对称故障时,形成零序电压;发生接地短路,零序电压的压降构成回路,从而形成零序电流。因此,零序电流只会出现在中性点接地系统的AG、BG、CG和ABG、BCG、ACG故障发生的情况下,而两相短路故障的AB、BC、AC不会出现零序电流。 图5 巴特沃斯滤波器与第一、第二类切比雪夫滤波器及椭圆函数滤波器频率响应的比较 将7个数据(Vaf,Vbf,Vcf,Iaf,Ibf,Icf,Iz)组成一组作为一个输入,通过仿真获得无故障和各类故障的三相电压和三相电流及零序电流数据共1 187组。各类故障数量如表2所示。将所有的故障数据以组为单位随机混合在一起,作为输入样本。 表2 所有故障类别及数量 表3表示的是在距离电源3 km的OH线路段发生各项不对称故障,FR=20, FIT=0.045 s时故障电压、电流和零序电流的情况。其余故障数据取不同线路位置,FR分别为30,45,60 Ω,FIT分别为0.050,0.060和0.065 s。 表3 故障电压、电流数据(标幺值) 将处理过的输入样本输入到神经网络中开始网络训练,经过100代左右的遗传变异后,种群的平均适应度和最佳适应度趋于稳定,意味着遗传算法收敛,逐渐逼近设定的目标要求。如图6所示,图中红色带“*”曲线代表平均适应度,蓝色带“△”曲线代表最佳适应度。 图6 适应度曲线 为方便BP神经网络输出结果统计,用二进制数1表示故障相,0表示非故障相,故9种不对称短路故障须使用4位二进制数表示,表4显示了不同故障发生时的逻辑关系。每组输入数据为7个,因此网络输入层节点为7个,输出结果为四位二进制数,故输出层节点为4个,隐含层节点数经过本文3.1节的方法设为12个。BP网络隐含层激励函数为tansig,隐含层输出计算公式为 (6) 式中:hj为隐含层输出;Xi为神经网络的输入;Wi j为前两层神经元的连接权值;bj为隐含层神经元阈值;j的范围为[1,n];n为中间层神经元数目。 输出层激励函数为purelin,输出为 (7) 式中:Ok为网络最终输出;Wjk为第2层和第3层的连接权值。图7展示了BP神经网络优化前后训练效果对比。 表4 故障类型逻辑表 图7 网络优化前后效果对比 可以看出,当优化后网络的迭代次数达到26次时,训练完成,网络的均方误差可达到期望的水平。而以同样的网络参数和训练样本训练未经优化的BP神经网络时,则需要迭代295次才能达到目标精度要求,优化前后对比明显,优化效果显著,有助于更好地进行故障分类。 表5 网络分类的正确率比较 利用Matlab/Simulink仿真模型获取的不同故障种类样本数据对基于GA-BP的高压混合输电线快速故障分类算法进行测试。将样本数据输入已经训练好的GAP神经网络,测试网络分类的正确性,统计优化前后神经网络识别故障的正确率,对比优化前后分类的效果,结果见表5。 可以看出:基于遗传反向传播神经网络优化的高压混合输电线快速故障分类算法具有较高的准确性,优化前的网络总体正确率为91.0%,优化后的网络最低正确率为97.3%,总体正确率达到98%以上。算法优化前后对比明显,正确率显著提高,能够准确判断故障类别,且故障分类时间较快,AG故障分类时间为2 ms,ABG故障分类时间为3 ms,AB故障分类时间为2 ms。 本文在通过经验选取隐含层神经元个数情况下,采用遗传算法优化下的BP神经网络进行高压架空线和地下电缆输电线路故障分类识别算法的研究。仿真结果表明:故障识别性能优异,分类准确率大幅提高,识别速度快,系统要求得到充分满足,有效提升了混合输电线路故障识别及诊断能力。 若考虑三相对称故障发生时,以及故障分别发生于架空线、地下电缆及其连接处的情况,则开展故障点定位研究需提高分类算法的识别性能和差异分辨精度。 [1] 丘映丹,李海锋,郭履星,等.基于异常点剔除的高压直流输电线路故障定位算法[J].电力建设,2015(12):91-96. [2] 宁一,王大志,江雪晨,等.基于原子能量熵和CSM的配电线路故障分类方法[J].东北大学学报(自然科学版),2017(1):1-5. [3] 孙鹏,曹雨晨,刘洋,等.采用二进制蚁群模糊神经网络的配电网故障分类方法[J].高电压技术,2016(7):2063-2072. [4] LIVANI H,EVRENOSOGLU C Y.A machine learning and wavelet-based fault location method for hybrid transmission lines[J].IEEE Transactions on Smart Grid, 2014,5(1):51-59. [5] 姚旭,程蓉,崔力心,等.面向智能变电站的输电线路综合故障定位方法研究[J].电力系统保护与控制,2016(11):40-45. [6] 高艳丰,朱永利,闫红艳,等.一种新型的输电线路双端行波故障定位方法[J].电力系统保护与控制,2016 (8):8-13. [7] 陈仕龙,谢佳伟,毕贵红,等.一种特高压直流输电线路神经网络双端故障测距新方法[J].电工技术学报,2015 (4):257-264. [8] 王伟,余锐,陈愚,等.特高压输电线路保护故障测距的应用研究[J].电力系统保护与控制,2013(19):40-46. [9] 宋国兵,蔡新雷,高淑萍,等.高压直流输电线路故障定位研究综述[J].电力系统保护与控制,2012(5):133-137,147. [10] 林圣,何正友,臧天磊,等.基于粗神经网络的输电线路故障分类方法[J].中国电机工程学报,2010(28):72-79. [11] 田晓文,马振利.基于GA-BP神经网络的转子故障诊断[J].重庆理工大学学报(自然科学),2015(7):44-48. [12] 董颖,刘欢杰,许宝栋,等.一种基于实数编码的改进遗传算法[J].东北大学学报(自然科学版),2005(4):219-221.2.2 BP神经网络的优化实现
3 仿真分析
3.1 输入数据采集与处理

3.2 网络训练

3.3 仿真结果分析
4 结束语

