结构光与双目视觉相结合的三维测量

张永举，顾旭波，张 健，王 兵，郭 玲

(1.江苏省特种设备安全监督检验研究院吴江分院,江苏 苏州 215200； 2.南京理工大学自动化学院,江苏 南京 210094)

0 引 言

随着近年来科学技术的进步，三维测量对社会生产和人们生活的影响日益增加。该技术能够对三维物体进行快速、精确的全尺寸测量，因此在工业产品设计与测量、文化影视娱乐、文物保护等诸多领域体现出良好的应用前景。

根据测量方式的不同，三维测量方法可分为接触式和非接触这2大类。接触式测量通过接触探头与物体表面接触获取物体三维结构，有测量精度高的优点[1]，弊端是测量速度慢，只能获得稀疏的测量数据，不适用于无法进行表面接触的被测物。非接触式测量可弥补以上缺陷。根据是否采用特定光源对被测物体进行照明，该类方法可进一步分为主动式和被动式。双目立体视觉法是一种被动式光学三维测量方法，其基本原理为:首先由不同位置的2台相机从不同角度同时拍摄同一场景得到2幅图像，然后检测和匹配同一物点位于2幅图像上的对应像点，最后基于视差原理计算得到该物点的三维数据[2]。该方法虽然原理简单，但对2台相机中对应成像点匹配困难，算法复杂。而编码结构光法作为一种新型的主动式光学三维重构方法，通过向物体投射编码结构光，使得待测物体在结构光的照射下生成特殊图像，该图像中包含了光源在被测物体上的畸变信息。然后根据三角法和相机与投影仪之间的参数进行计算，获得物体表面的三维坐标值[3]。结构光技术解决了特征点搜索困难的难题，但由于投影仪并非成像设备，标定难度高，精度低，从而对三维点云的计算产生了极大的影响。目前常用的投影仪标定方法有反成像法、三角测量法和多项式拟合法这3大类。反成像法操作简单，但是由于在依赖相机标定结果的基础上进行标定，投影仪标定进度低于相机标定一个等级；三角测量法和多项式拟合法精度高，但是标定过程复杂，安装约束性强，不适用于实际操作。

本文将双目立体视觉测量和结构光测量这2种方法相结合，在完成双相机的空间位置获取后，对获得的编码图案进行解码，从而获得物体上各点的三维数据。该方法回避了传统立体视觉中稠密匹配和编码结构光中投影仪标定这2个难点，简化了对应点匹配算法的复杂度，提高了三维测量的精度[4]。

1 相机标定和校正

对于双目立体视觉成像技术，相机标定是三维信息获取的一个关键步骤，其标定结果的精度和速度将直接影响之后的三维测量结果[5]。在双目立体视觉中，因为2台相机的参数配置相同，就可以把双目立体视觉系统标定转化为先对单个相机进行标定，再根据双目视觉原理对双目相机进行标定[6]。

1.1 单相机标定和校正

在标定时，将相机视为理想化的针孔照相机模型，如图1所示。其中点Oc为照相机光心和世界坐标系原点，点o为图像坐标系原点，xoy为相机成像平面，点P(Xw,Yw, Zw)在图像物理坐标系中为点p(xp,yp)。

图1 针孔照相机模型

通过三角形的相似性原理可以得知世界坐标系中点P与相机像素坐标系中对应点关系为：

(1)

式(1)中，s为尺度因子，(u,v)为点P在图像中像素坐标点，(Xw,Yw,Zw)为点P在世界坐标系中坐标点，αx,αy归一化焦距，(u0,v0)为相机主点，R为旋转矩阵，T为平移向量，A为相机内参数矩阵，H为单应矩阵。

由于相机中透镜结构特点会导致获取的图像存在畸变。畸变一般分为径向畸变和切向畸变，尤其以径向畸变最为突出。因此，忽略切向畸变，采用以下模型进行畸变校正[7]：

(2)

式(2)中(xd,yd)为实际检测到的坐标，(xu,yu)为理想坐标[8]。

张氏标定法把世界坐标系构造在Zw=0的平面上，简化矩阵得[9]：

(3)

单应矩阵为：

(4)

由于R为旋转矩阵，可得约束条件：

(5)

对于n幅图片，其中每幅图片含有m个标定点，则可获得2mn个方程。解得相机内外参数后，再考虑相机畸变的条件下，以此为初值，用阻尼最小二乘法提高计算精度。

1.2 双相机标定和校正

双目标定的是双目视觉系统中2台相机之间的相对位置关系，即得到2相机坐标系间相对的旋转矩阵和平移向量[10]。

世界坐标系中任意一点P在左右2个相机坐标系中可表示为：

(6)

其中P1,P2为点P在2相机所成图像中的像点，R1,R2为2相机世界坐标系到各自相机坐标系的旋转矩阵，T1,T2为2相机世界坐标系到各自相机坐标系的平移向量。由式(6)可得：

(7)

如图2所示，点P1,P2为立体校正前点P在左右相机中位置，c1,c2为左右相机的光心，2点之间的连线为基线，e1,e2为左右相机的成像平面与基线的交点，也就是极点。由极线约束条件可知，左图像中点P1在右图像中的对应点必定位于直线e2P2上，极线约束令对应点的搜索由二维搜索降为一维搜索[11]。但极线往往为一条斜线，为了进一步降低搜寻对应点的复杂度，还需要进行极线校正。

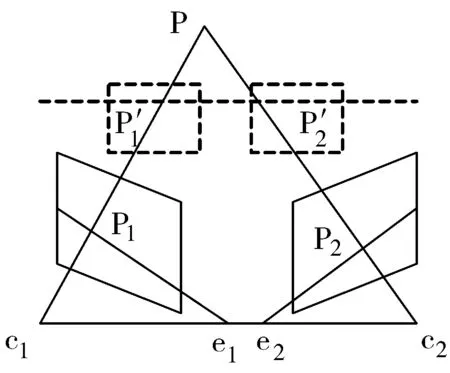
图2 双目视觉系统

(8)

2 结构光编解码

结构光法是一种主动式的对被测物体进行特征点标记的方法，通过向物体投射特定图案使被测物体具有容易识别的编码特征信息，解决了双目视觉中“像素匹配”的难题[12]。根据编码方法的不同，解码方法也不一样，但基本原理一样。结构光编解码就是利用图像上灰度、几何、颜色等可视性特征来给予像素点先验编码信息，然后由相机获取调制图像，最后对调制图像进行解调，得到特征点码值[13]。

2.1 结构光编码

在二值编码中，应用最广的就是格雷码编码。格雷码图像只使用黑白2种颜色来区分不同的条纹，分别记为0、1，将这2种条纹进行不同时间序列的组合便可得到对应于每一条条纹的编码。格雷码编码作为一种可靠性编码，从当前状态转到下一状态只存在一位跳变，降低了解码过程中的错误率。格雷码编码具有精度高、求解过程简洁、误差小和受环境影响小的优点，缺点在于需要投射大量图案，分辨率低。而相移法是向物体表面周期性投射正弦周期位移图像，在一个周期内每点相位值绝对唯一。该方法具有很高的分辨率，但无法判断不同周期内相位值，具有二义性。综上考虑，本文选择使用了格雷码与相移法相结合的编码方式，使其兼具二者优势，即格雷码条纹编码确定性和鲁棒性加上相位移法的高分辨率。

首先由投影仪依次向物体投射如图3所示的6幅格雷码图案，将物体表面分成000000～111111这26个区域。其中码字为6幅图案所对应的0、1的序列，0对应黑色，1对应白色，如图3(a)中点P为000111。然后再向物体投射如图3(b)所示的相移图案，并将其每次平移1/4周期，投射4次。此外，需满足格雷码图案的最小周期为相移图案周期的4倍，从而使得格雷码周期内相移图案每点相位值绝对唯一[14]。

(a)格雷码编码 (b)相移编码图3 编码图案

2.2 结构光解码

与上述编码方法相对应的解码方法中，首先将格雷码转换为十进制编码，获得周期次数k[15]。为了减少物体表面颜色对测量结果的干扰，本文通过简化的Daniel Scharsterin[16]方法，在向物体表面投射一组格雷码图案后，对格雷码取反，再次投射到物体上。若第一组格雷码采样点灰度值大于第二组，则取值为1，反之为0。该方法减少了阈值分割产生的错误，提高了周期值k的精度。

然后，投射4幅相移图案，采样点的灰度值可表示为[17]：

In(x,y)=I′(x,y)+I″(x,y)[cos θ(x,y)+nπ/2]

(9)

式(9)中In(x,y)为点I(x,y)在第n幅相移图中的灰度值，I′(x,y)为条纹光的背景光强，I″(x,y)/I′(x,y)为条纹反差，θ(x,y)为待求主相位值：

(10)

最后，将格雷码解码所得周期值与主相位值相叠加可得点I(x,y)的绝对相位值ψ(x,y)：

ψ(x,y)=2kπ+θ(x,y)

(11)

2.3 周期校正

在完成双目相机立体校正后，即可采用格雷码与相移法相结合的结构光测量方法对物体进行三维测量。主要步骤总结如下：

1)用格雷码对待测物体表面进行粗略划分，计算得到格雷码周期；

2)投射相移图案细分测量区域，以此获得更高的分辨率，得到主相位值；

3)与格雷码结合去除相位包裹，得到整个测量区域的绝对相位。

理想情况下，格雷码条纹与相移图案周期完全相同，周期次数k与相位主值θ同时突变，绝对相位值ψ单调递增[18]。然而受环境因素干扰，两者之间一般存在着周期错位，即ψ(x,y+1)-ψ(x,y)≈2π。考虑环境影响，当ψ(x,y+1)-ψ(x,y)≥3/2π，令k(x,y)=k(x,y)+1，以确保格雷码条纹与相移周期一致。

3 实 验

为验证基于结构光的双目三维测量方法的可行性，搭建如图4所示的三维测量系统，包括2个焦距为12 mm的M1214-MP2-computar镜头，一台Acer K132投影仪(分辨率为1280×800)和电脑一台。

图4 三维测量系统

被测物以吊钩为例，考虑到吊钩表面为黑色，会吸收所有色光，导致相机无法拍摄到物体条纹图像。即在投射结构光时，图像上物体每点始终为黑色，灰度值始终为0。为了更好地对物体进行三维重构，降低物体表面颜色的影响，应先向物体表面喷涂反差增强剂FC-5，形成一层白色薄膜，增强视觉反差。

在利用棋盘完成双相机的标定后，向物体依次投射格雷码和相移图案，采集处理左右相机拍摄到图像，生成物体模型。如图5所示，其中图5(a)为投射格雷码图案的图像，图5(b)为投射相移图案的图像，图5(c)为吊钩实物图，图5(d)为测量得到的点云并重建表面的结果。

(a) 格雷码图像 (b) 相移图像

(c)吊钩实物图 (d)吊钩模型图5 吊钩实物及测量数据

为了验证三维测量的精度，选择吊钩上的字母“1”，“K”的边角点A,B,C，在测量数据中计算任意2点间的距离，并与单目结构光测量结果作比较，结果如表1所示。在表1中，测量距离1和绝对误差1为双目结构光测量结果，测量距离2和绝对误差2为单目结构光测量结果。实际距离采用SATA91511数显式游标卡尺测得，精度为±0.02 mm。

表1 三维测量误差分析/mm

采样点指标项实际距离测量距离1绝对误差1测量距离2绝对误差2AB13．1413．050．0911．911．23BC75．7575．330．4275．070．68AC66．9667．310．3567．410．45

由表1可知，采用双目结构光测量提高了测量的精度，三维测量误差精度达到了毫米级，能够很好地反映物体三维形貌。

4 结束语

三维测量技术在工业产品测量与设计、文物保护、医学检测等方面有着重要的作用，如何提高三维测量的精度和速度，减少环境的影响则是三维测量技术的重点和难点。本文将结构光技术与双目视觉系统相结合，回避了传统双目视觉中匹配困难和结构光测量中投影仪标定困难的2个难题，优化了系统设计，提高了测量的精度。在简单论述相机标定和结构编解码的原理的基础上，进行了实验，论证了方法的可行性。实际测量中，有时除了获取物体三维数据外，还需获取其表面纹理信息，笔者今后将致力于物体的纹理映射和多角度的点云拼接方法的研究。

[1] 赵小辉,丁玲,王磊. 三维光学形貌测量系统在飞机研制中的应用前景[J]. 民用飞机设计与研究, 2012(S1):11-15.

[2] 李靖,王炜,张茂军. 双目立体视觉和编码结构光相结合的三维重建方法[J]. 计算机应用, 2012,32(S2):154-158.

[3] Sotoodeh S, Gruen A, Hanusch T. Integration of structured light and digital camera image data for the 3D reconstruction of an ancient globe[C]// The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. 2008:367-372.

[4] 涂颜帅. 基于时间频率编码的高速光学三维测量及应用研究[D]. 金华:浙江师范大学, 2015.

[5] 胡亚利,马兆敏,胡蓉,等. 基于视觉测量障碍位置的车载摄像机标定[J]. 科学技术与工程, 2014,14(31):249-251.

[6] 杨宏伟,陈利峰. 新型双目相机运动控制系统设计[J]. 长春理工大学学报(自然科学版), 2015,38(6):108-113.

[7] 李芳芳. 透镜畸变校正算法比较分析[J]. 测绘, 2010,33(5):225-228.

[8] Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000,22(11):1330-1334.

[9] 刘宝元,邢冀川. 基于激光三角法货车体积测量系统的标定研究[J]. 光学仪器, 2015,37(3):189-194.

[10] 卢传泽. 双目立体视觉三维信息获取技术研究[D]. 广州:广东工业大学, 2013.

[11] 余洪山. 主动立体视觉关键技术及其应用研究[D]. 长沙:湖南大学, 2003.

[12] 阳光. 一种结构光法测量物体深度的方法及装置:CN103322937A[P]. 2013-09-25.

[13] 马俊. 基于结构光的双目立体测量[D]. 哈尔滨:黑龙江大学, 2016.

[14] 宋昌江. 基于双目视觉的三维物体表面测量系统设计与实现[D]. 哈尔滨:哈尔滨工业大学, 2012.

[15] 朱昱. 数字条纹投影三维形貌测量技术[D]. 合肥:合肥工业大学, 2014.

[16] Scharstein D, Szeliski R. High-accuracy stereo depth maps using structured light[C]// Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2003,1:I-195-I-202.

[17] 王洋. 基于中国剩余定理的模拟编码结构光三维测量方法研究[D]. 哈尔滨:哈尔滨理工大学, 2014.

[18] 姜涛. 反求工程中融合特征捕捉的光学三维测量方法研究及系统开发[D]. 上海:上海交通大学, 2005.