基于ALS模型协同过滤推荐算法的优化
倪满满
(1.武汉邮电科学研究院,湖北 武汉 430074; 2.南京烽火软件科技有限公司,江苏 南京 210019)
0 引 言
信息过载问题在网络及电子商务的普及下变得愈加严重。推荐系统可以根据用户的基本信息及历史行为挖掘出用户所需信息并主动向用户或者物品提供个性化推荐服务。推荐系统发展至今已经拥有20多年的历史[1],因其庞大的应用需求,推荐系统已经得到了广泛的关注。推荐系统是解决信息过载的一种重要手段。目前信息推荐的方法主要包括:混合推荐方法、基于内容的推荐方法和协同过滤推荐方法[2],其中协同过滤方法是推荐系统中推广最成功和应用最广泛的推荐方法之一。
近年来对协同过滤推荐算法的研究如火如荼;在2013年、2015年国外著名学者Aberer等人[3]和Ma等人[4]分别从相似度计算和数据来源单一入手提高推荐系统的准确性,同时在这其间国内著名学者韩立新和马兆才提出一种全新的策略:引入自适应信任算法[5]和自组织神经网络(SOM)[6]来改进协同过滤推荐算法,提高推荐系统的准确性。以上对推荐系统的研究,都有效地推动了协同过滤推荐算法的发展,但是并未考虑推荐系统的时效性问题。本文将从时效性和准确性两方面进行推荐系统的研究。
在解决时效性问题时,考虑到在单节点上实现这些方法,计算速度变得非常慢,时延也较长、时效性差[7],本文采用多节点的分布式系统并行化实现方法,并对比分析目前主流的分布式计算平台Hadoop和Spark,选择时效性较高的实现方式,设计时效性较高的推荐系统,提高推荐系统的时效性。在提高推荐系统的准确性方面,考虑到一般推荐算法的思想是通过用户及物品之间的相似性进行预测评分,从而给出个性化推荐结果,故本文从相似性计算和预测评分入手,引用ALS模型,在模型训练前融入物品的相似性信息,设计一种新的损失函数;同时考虑到时间遗忘会影响兴趣变化,在最优模型得出的评分中引入兴趣遗忘函数。通过以上的改进,有效地提高推荐系统的时效性和准确性。
1 推荐系统
推荐系统是什么?前面只是粗略地说可以处理信息过载问题。其实解决信息过载问题有2种方式:1)信息拉取;2)信息推送。其中信息推送就是推荐系统,维基百科曾定义推荐系统为信息过滤系统的一个子集,目标在于推测一个用户对物品的喜好或者评分等级[8]。
目前推荐系统已经被普遍应用于购物平台、娱乐休闲平台、社交等平台中。推荐系统之所以被应用这么广泛,因为它不仅可以在信息过载的环境中,向用户推荐商品进行单向的信息传递,而且还可以实现客户和企业的双向信息传递。企业可以通过推荐系统向企业推荐既有价值又有潜力的客户[9]。目前人们所熟悉的电影、视频网站、QQ、微信、阿里巴巴淘宝及亚马逊等都在使用推荐系统。其中亚马逊堪称推荐系统中最成功的案列。推荐算法是推荐系统的核心,故本文着重研究推荐算法。
2 推荐算法
2.1 基于ALS模型的推荐算法
协同过滤推荐算法近年来被大范围地推广,对该算法研究最热的3个算法为:基于用户的协同过滤算法、基于物品协同过滤算法和基于隐语意的协同过滤算法[10]。本文着重研究基于隐语意的协同过滤推荐算法,该算法将用户-物品评分矩阵分解成2个低维的矩阵乘积,分别为用户的喜好因子向量和物品的属性因子向量。通过用户和物品因子向量的相乘就可以预测相应用户对指定物品的评分,同时2个因子向量的计算互不干扰,影响因素较小,因此对基于隐语意的协同过滤算法的研究颇有学术价值。
基于隐语意模型的协同过滤推荐算法实质是填充用户-物品评分矩阵中缺失的部分,矩阵中的每一个元素代表用户u对物品m的评分,根据矩阵奇异值分解原理,可以将用户-物品矩阵分解成几个矩阵相乘的形式[11],假设用户-物品评分矩阵为S,则运算表达式如式(1)所示:
S′=UTM
(1)
其中矩阵U(Ul×m)代表用户喜好因子参数(行),M矩阵(Ml×n)代表物品的隐语意属性参数(l< 图1 矩阵分解 通过用户-物品评分矩阵分解原理可知,想要预测用户对物品的喜好只要求取用户因子向量和物品因子向量即可;一般对U和M的求取是通过最小化损失函数[12],因此对于隐语意模型来说对损失函数的定义非常重要。本文采用的损失函数如式(2)所示: p′=∑ij(S-S′ )2=∑ij(S-UTM)2 (2) 为了防止损失函数过拟合,采用正则化方法添加正则化项,最后损失函数如式(3)所示: p(u,m)=p′+ λ(‖U‖2+‖M‖2) = ∑ij(S-UTM)2+λ(‖U‖2+‖M‖2) ∑inui‖ui‖2) (3) 对损失函数的优化有梯度下降法和最小二乘法,其中梯度下降法是局部最优,最小二乘法是全局最优。本文采用全局最优法:最小二乘法(ALS)。最小二乘法的基本思想是:固定用户或者物品属性因子中的一个元素,交替求取另一个,反复迭代,直至RMSE值为最小时得到最优评分预测模型[13]。 依据ALS模型推荐算法原理可以发现,基于ALS模型的协同过滤推荐算法的核心是将用户-物品评分矩阵设计成用户隐形因子U和物品隐形因子M相乘的形式,通过优化损失函数求取U,M;最终通过U与M的乘积增加用户-物品评分矩阵元素,在一定程度上缓解了数据稀疏的问题[14]。 矩阵U及M在初始时是随机生成的,求取相对独立,影响因素较小,且复杂度较低,实现简单,相对来说是一种不错的推荐算法。但是结合常见的推荐算法可以发现,基于ALS模型的推荐算法未考虑:1)相似度问题;2)随着时间的推移兴趣遗忘问题。针对相似度问题,本文将引入物品相似性,因为在类似电影推荐系统或者电子商务等网站中,用户的数量远超物品的数量。同样基于这个原因,在计算物品相似度的时候,每一件物品拥有众多用户行为数据,因此最终评分的预测准确度要高于基于用户的协同过滤算法。因此在此处加入物品相似度计算。关于物品相似度的计算方法目前主要有:余弦相似度方法、皮尔逊相关系数、修正的余弦相似度[15]。本文选择修正的余弦相似度,则此时损失函数的表达式如式(4): (4) 针对时间因素的影响,本文在最优评分预测模型的基础上引入兴趣遗忘函数。该方法是对优化后的模型进一步优化。它考虑了随着时间的推移,人们对事物的印象会有所衰减,将会直接影响兴趣的变化,如果依然按照以前的喜好使用推荐系统,最终的推荐结果绝对会与客户当前的喜好有较大的差距,引入兴趣遗忘函数可以追踪用户兴趣变化,可以在一定程度上有效地提高推荐系统推荐结果的准确性。本文借鉴艾宾浩斯遗忘曲线构造用户兴趣遗忘函数。艾宾浩斯遗忘曲线是由著名心理学家艾宾浩斯在大量的实验基础上发现的人类自然遗忘规律:开始的时候,人的遗忘是非常快的,到了后面人的遗忘曲线就变得缓慢,最终趋于稳定。 艾宾浩斯曲线函数表示如式(5)所示: (5) 其中L为随着时间推移记忆的保存量,c、k为控制变量,t为从对事物的认知开始到当前时刻的时间间隔(单位:分),经过艾宾浩斯的大量研究发现,当c=1.25,k=1.84时,遗忘曲线的变化和人类记忆的变化最为接近[16]。故引入遗忘曲线后的用户物品评分表达式如式(6)所示: (6) 其中fij为引入用户物品相似性计算后所得最优模型中用户i对物品j的评分,rij为引入遗忘函数后用户i对物品j的最后预测评分。 经过优化后的算法流程如图2所示,其中虚线部分为本算法的改进部分。 本文搭建的Spark集群采用的是3台普通PC机,包括1个Master节点和2个Slave节点,3个节点均为Ubuntu14.10系统,节点之间通过局域网连接,实验所涉及的软件及版本为:Java JDK 1.7,Hadoop 2.6.0,Spark1.2.0;开发工具为Eclipse。 图2 改进后的推荐算法流程图 实验数据方面采用公开的MovieLens数据集。MovieLens数据集是由研究中心录入的关于MovieLens网站真实的用户对电影的评分数据[17]。MovieLens有3种数据集,数据集的大小有100 kB,1 MB,10 MB;100 kB的数据集拥有10万条评价结果,1 MB的数据集拥有100万条数据,10 MB的数据拥有1000万条数据。课题在实验中选取的是100 kB(10万条),1 MB(约100万条)这2种数据集[18]。 实验设计了2类测试:1)单节点及分布式环境下推荐系统的时效性测试;2)基于ALS模型推荐算法改进前后的准确性对比测试。 关于推荐系统时效性测试的实验设计:分别采用1万、10万和100万条数据在单节点及2个分布式计算平台Hadoop和Spark上实现推荐算法,测试基于ALS模型在不同环境下实现推荐的速度,其中1万条数据随机从100 kB的数据集中抽取;实验结果如图3所示。 图3 推荐结果时效性比较 基于ALS模型推荐算法改进前后准确性的实验设计:分别采用没有融入物品相似度且未在评分预测中引入兴趣遗忘函数的推荐模型,和在损失函数中融入物品相似度并在评分预测中引入兴趣遗忘函数的推荐模型;验证改进后的推荐模型是否提高了推荐结果的准确性。实验是在同样的数据集、迭代次数和属性个数情况下,进行模型改进前与改进后的RMSE值的对比,实验结果如表1所示。 表1 算法优化前后RMSE值对比 iterRMSE值ALSALS_USALSALS_USALSALS_US81012200.9010240.8954120.9006820.8929390.9045430.898615300.9003790.8916290.9009880.8910950.9028650.897305400.9009150.8914110.9003680.8861190.09022630.894612 图3对推荐系统在单节点、Hadoop和Spark上面运行的时效性对比,由图3可以看出,数据量无论为多大时,单节点的推荐系统都比多节点的推荐系统耗时更长;对多节点的分布式计算框架进行对比可以发现,当数据量很小时,Hadoop与Spark的运行时间差别不大,但当数据量越大,Spark比Hadoop耗时更短,而且当数据量增大时,Spark的运行时间上升趋势比较缓慢,Hadoop的上升趋势比较快速,可以想象,当数据量非常大时,Hadoop运行将会非常慢,从而不能够及时地向用户推荐当下喜欢的物品。以上结论验证了该算法在采用Spark分布式并行化计算时有效地提高了该算法的时效性。 表1是基于ALS模型推荐算法优化前后RMSE值的统计结果。表1将优化前后的算法在不同的迭代次数、属性个数下的实验结果进行对比,可以发现优化后的ALS模型训练方式都可以减小其RMSE值,并且随着迭代次数的增加,优化效果越突出;当迭代次数为40属性个数为10时RMSE值可以降到0.886119;虽然优化后的结果不是那么明显,但是优化后的基于ALS模型的推荐系统在准确性上确实有所提升。 本文在对前人推荐算法研究的基础上,着重研究了基于ALS模型的推荐算法,让其分别在单节点和多节点的分布式框架上实现,对比单节点及不同分布式环境下推荐系统的时效性;另外在基于ALS模型的损失函数上融入物品相似性计算,在最优模型的用户物品预测评分中引入遗忘函数,从而进行实时准确地推荐,本文在推荐系统中作了上述改进后有效地提升了推荐系统的时效性和准确性。当然也存在着不足:如在相似性计算上未考虑用户相似性,在遗忘函数的设计上未考虑其他影响因素:用户可能因朋友的提醒而引起对事物的重新认知,使得记忆衰减趋势会有所改变,从而导致推荐结果不够准确,这是接下来笔者要研究的方向。 [1] Ricci F, Rokach L, Shapira B, et al. Recommender Systems Handbook[M]. Springer-Verlag, 2011:1-35. [2] Hussein T. Context-aware recommender systems 2011 [C]// ACM Conference on Recommender Systems. 2011:349-350. [3] Liu Xin, Aberer K. SoCo: A social network aided context-aware recommender system [C]// Proceedings of the 22nd International Conference on World Wide Web. 2013:781-802. [4] Ma Tinghuai, Zhou Jinjuan, Tang Meili, et al. Social network and tag sources based augmenting collaborative recommender system[J]. Ieice Transactions on Information & Systems, 2015,98(4):902-910. [5] 黄文亮,韩立新,曾晓勤,等. 一种基于自适应信任计算的推荐系统算法[J]. 计算机应用与软件, 2013(11):42-44. [6] 马兆才. 基于协同过滤的推荐系统算法研究与实现[D]. 兰州:兰州大学, 2015. [7] Shani G, Gunawardana A. Evaluating recommendation systems[M]// Recommender Systems Handbook. 2011:257-297. [8] Marinho L B, Nanopoulos A, Schmidtthieme L, et al. Social tagging recommender systems[M]// Recommender Systems Handbook. 2011:615-644. [9] Manouselis N, Drachsler H, Verbert K, et al. Recommender systems for learning[M]// Springerbriefs in Electrical & Computer Engineering. 2012:97-98. [10] Adomavicius G, Sankaranarayanan R, Sen S, et al. Incorporating contextual information in recommender systems using a multidimensional approach[J]. ACM Transactions on Information Systems, 2005,23(1):103-145. [11] 刘鲁,任晓丽. 推荐系统研究进展及展望[J]. 信息系统学报, 2008(1):82-90. [12] 杨志伟. 基于Spark平台推荐系统研究[D]. 合肥:中国科学技术大学, 2015. [13] 李改,潘嵘,李章凤,等. 基于大数据集的协同过滤算法的并行化研究[J]. 计算机工程与设计, 2012,33(6):2437-2441. [14] 车晋强,谢红薇. 基于Spark的分层协同过滤推荐算法[J]. 电子技术应用, 2015,41(9):135-138. [15] 张明敏. 基于Spark平台的协同过滤推荐算法的研究与实现[D]. 南京:南京理工大学, 2015. [16] 李克潮,梁正友. 适应用户兴趣变化的指数遗忘协同过滤算法[J]. 计算机工程与应用, 2011,47(13):154-156. [17] 任磊. 推荐系统关键技术研究[D]. 上海:华东师范大学, 2012. [18] 郑炳维. 基于Spark平台的协同过滤算法的研究与实现[D]. 广州:华南农业大学, 2016.
2.2 推荐算法的优化

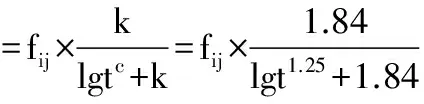
3 实验及结果分析
3.1 实验环境与数据

3.2 实验设计


3.3 试验结果对比分析
4 结束语

