数学好玩、玩好数学——追求会想、会用、会学的教学

◇张思明

“数学就是一些居心叵测的成年人为青年学生挖的陷阱”“数学就是那些仅仅出现在课本和试卷上的，让某些老师看着学生崴脚而感到窃喜的东西”……在学生心目中，老师不过就是一些挖坑布雷的高手。当我们在为学生被我们的一肚子题折腾得晕头转向而沾沾自喜时，我们离数学的真谛、离数学教育的真谛就越来越远了。

正如刘坚教授所言，我们要带给学生的，应是学生成长所需要的那种文化素养，是知道源和流的数学。

一、真实课堂中的数学应用

我在六年级课堂上做了一节数学思维的实验课，借由“怎么会想”“怎么会用”两个层面的题目，让学生向“怎么会学”升华。

（一）怎么会想——培养学生的数学思维。

一张扑克牌剪掉1个角（剪痕是直线），还剩几个角？最基本的答案是还剩5个角，这也是大部分学生能想到的。只有的学生能很有把握地进行反驳，他们用画图的方式解释可能会剩3个、4个、5个角，但如何把它们串起来，对于学生而言是个难题。

这中间存在着一个思维的逻辑链条：先把5个角这种最基本的情况作出来（如图1）；两个点在两条边上运动，按住一个点P，让另一点Q上下运动，当运动到点B时，自然得出还剩4个角的情况；再把点Q（B）按住，让另一点P左右移动，当运动到点D时，得到还剩3个角的情况。学生掌握了这种思维方法，就可以进入下一个问题环节。

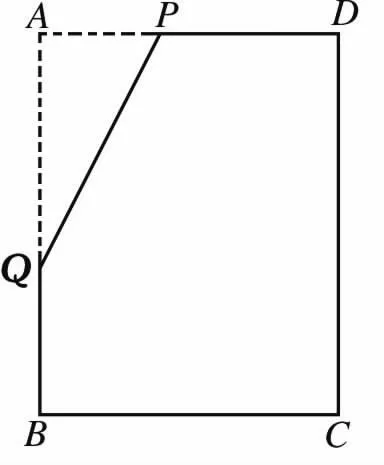
图1

一个正方体用平面砍掉“1个角”——实际上是砍掉1个三棱锥，还剩几个面、几个角？先呈现一个任意的结果，再固定两个点，让另一个点运动……利用刚才的思维方法去想，学生很快就推出了其他结果。

将一个西瓜横竖各平行地切两刀，吃完后剩下几块皮？学生不再对书上所给的“10块”这一标准答案深信不疑，纷纷表示随便给出一个结果，就可能会有更多的东西需要思考。那么，如何思考？10块的确是一个结果，但刀口是可以挪动的。得到启示后，班上的学生开始躁动了。一些学生急着得到结果，却很少尝试思考为什么剩下的西瓜皮会变少。学生容易针对极端情况，得出剩下6块西瓜皮这种情况，这时，教师可以引导学生有意识地探索剩下7块、8块、9块甚至5块西瓜皮的情况。

对于这样的题目，我们强调更多的是思维，是找到这些结果的过程。学生要“会想”，而“会想”又存在着很多“技巧”，这个“技巧”或者是先猜测一个最基础的结果，再固定一些可以变化的条件，让另一些条件变化，在变化的过程中就会出现各种各样的结果；或者是想极端情况，先想出最多的结果，再想出最少的结果，然后找出中间值的情况。

（二）怎么会用——培养学生的问题意识。

数学学习的重点不是仅仅针对问题得到一个具体的答案，而是希望培养学生提出更多问题的问题意识。教学不是上课、下课的过程，而是不断发现和提出新问题的过程。有了数学思维，我们又可以提出很多问题。例如，图2中包含多少个正方形？

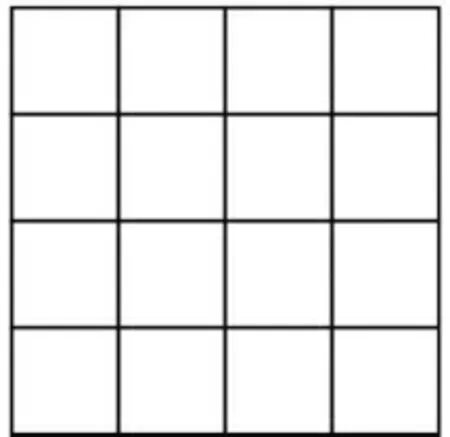
图2

数的过程很重要，需要不重、不漏，先数16个小“口”，再数2×2的田字格，然后数3×3的，最后数最大的这个，这样一种一种数下去的过程，正好培养了学生图形分类的思考能力。

据此，学生会自己提出问题吗？比如，推广到三维的情况（如图3），图中有多少个正方体？再如，推广到平行四边形、三角形的情况（如图4、5），图中分别有多少个平行四边形、三角形？对于图4、5，更一般的结论是什么？改变维数又有什么问题和猜想？

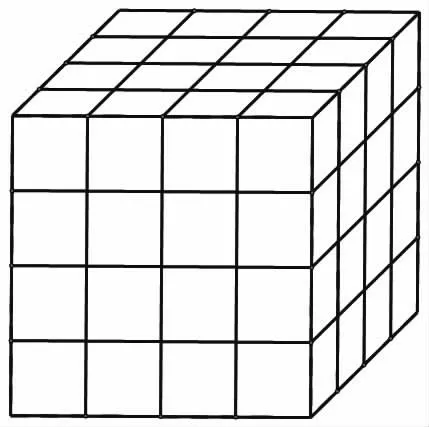
图3

图4

图5

……

到最后，已经不是学生能不能解决这个问题，而是学生能不能提出这样的问题，问题永远比结果重要，要激发学生去思考。我们总习惯于要把书本上的知识点完完整整地灌输给学生，其实更重要的是“问题场”的概念，学生走进你的教室，就是生活在一个“问题场”里，永远不是进行到“老师问‘同学们还有问题吗’，学生答‘没有啦’”就结束了，而是学生走出教室后还会有更多的问题。

如此我们便能发现很多有意思的事情，比如，用纸折出正多边形这一实践中，正三角形、正五边形、正六边形学生都能顺利折出，折到正八边形的时候，他们是这样做的：先折出3×3的方块，再把4个角折起来（如图6），这样折感觉既很“正”，又为八边形，学生认为这样折出来的就是正八边形。这时，不急于评判的教师会发现，一部分学生观察到这个“正八边形”的边长并非完全一样，并且尝试做出了修改，修改的策略是五花八门的……这恰好就是学生发现问题、解决问题的过程。

图6

（三）怎么会学——培养学生的学习能力。

1.让学生知道数学的价值。

学习讲究的是思维，就拿背公式来说，部分学生虽然能够把公式背得滚瓜烂熟，但一问起稍微“超纲”（教师没有教过）的，学生就不会了，这说明学生并没有真正理解这些公式是怎么得到的。很多教师感觉自己教得很卖力，但发现学生并非知识学得越多，问题就解决得越好。比如，要求螺旋形蚊香的真正长度，高中生想到了等速螺线，初中生把蚊香近似看成了一个圆，而小学生则解下鞋带铺在了蚊香上。会背公式不算本事，把知识学活了，这才是学习应追求的东西。学生要知道数学的价值，知道数学有用、可用、能用，并且想用、会用、善用数学。

2.让学生学会独立思考。

图7

北京大学校园内东南角的燕园大厦下有一个“双莫比乌斯带”形状的雕塑（如图7），初一学生看到了什么呢？炸糖耳朵、炸焦圈……学生把它和吃的联系了起来，我没有进行批判，而是让他们每天都去看，直到看明白为止。到了高三，一个学生跑来说他看明白了，他说这个雕塑说明了“真理和谬误只差一步”，他把一条一面是红、另一面是蓝的纸带照着捏了一下并粘了起来，想象在蓝面上走，走到黏合处，一脚跨过去就走到了红面上，从而形成了他对这个雕塑的理解。教师要站得更高，我们的教育不在于是否算得更快，不在于多一个、少一个的知识，而在于这样的渗透，在学生心里埋下一颗种子，让他们知道其实最有价值的东西，就在自己每天的成长和发展中。

教师不要一味地只当“强者”，把自己包装成什么都知道的形象，总是呈现高明的一面，而是要学会“装傻”，以培养学生的自信心和独立思考的能力，甚至在任何学科中，都应该有意识地让学生站起来批判我们。正如王尚志老师所说：最伟大的老师是让孩子站在你的肩膀上，孩子还以为自己就是长得那么高。

二、基础教育中的数学应用与创新

近些年来，数学从台后走到台前，成为了创造价值的工具。美国国家数学教育顾问委员会在报告“成功的基础”中有言：经研究证明，在美国，平均地看，数学好的人收入就高。

现代社会中，随处可见数学模式。就以大数据为例。根据震动中心所提供的数据，日本电视台可以及时、准确地发布地震相关信息；根据各大药店所售药品的相关数据，美国疾控中心可以迅速监测到传染病的发生；分析手机里的运动轨迹、覆盖面积等数据，保险公司可以清楚地了解每个人的身体状况……

（一）从应用到建模的教学层次及建议。

从《数学建模教学与评估指南》一书可以看到，美国的学校很早就让学生开始学习数学的应用与建模。就拿午餐的问题来说，学前班到二年级，可以收集数据，讨论一个组要吃掉多少胡萝卜，哪些食物与胡萝卜搭配最好，多大的餐盒可以装下这些胡萝卜……三至五年级，可以进一步讨论胡萝卜和其他蔬菜营养成分的比较，如何在各种食物中挑选组成最佳的午餐，怎样安排各餐的品种和价位……六至八年级，基于选择的数量范围（成分、价格、是否送餐、口味等）决定购买哪种披萨饼，给披萨饼的售价找一个函数（自变量可以是直径或配送时间等）……这些项目学习，都是非常有应用价值的。

在我们的建模实践中，提出了从数学应用意识渗透到完整的数学建模活动的8个逐步推进的层次：

（1）创设为帮助学生理解概念、函数、定理、公式等而有意设计的实际情境。

（2）直接套用数学概念、函数、定理、公式等，给出有实际意义的结果（如函数值），或者解释、说明得到结果的实际意义。

（3）通过简单的变换，间接套用数学概念、函数、定理、公式等，给出有实际意义的结果。

（4）教师或教材给出实际问题，并带领（教材是引领）学生完成数学化及简单、具体的数学应用。

（5）教师或教材给出实际问题，学生自主完成数学化及简单、具体的数学应用。

（6）教师或教材给出问题情境，学生自主提出实际问题，师生一起完成“建立模型”和“模型求解”的主要过程。

（7）全过程（选题、开题、做题、结题）、学生部分自主（在发现和提出问题、模型的选择和建立、求解模型、给出模型结果的解释等环节中，教师部分参与，给予指导和支持）的数学建模活动。

（8）全过程、全自主（学生自主发现和提出问题、自主完成数学化的建模过程、自主求解模型、自主给出模型结果的解释，在整个过程中可以自主寻求教师的帮助）的数学建模活动。

要使小学和初中衔接，就得做到前两个层次，让小学生体会到数学是从生活中来并运用到生活中去的。

（二）关于数学应用的一些教学案例。

有一天，路边的一则广告引发了我的好奇心：“本部承接超大型工程图纸复印业务，规格可达A1、B1大小……”我们常用的复印纸型号有A4、A5、B4、B5等，那么，A1、B1复印纸有多大？能否根据手边常用的复印纸大小，推算出A1、B1复印纸的大小？它们的尺寸之间有什么数量关系？通过分析递推关系我们发现：只要知道A系列纸的一条边，就能推出其所有的边长，B系列纸也同样如此，甚至只要知道任意一条边，就能推出A、B系列所有复印纸的边长。

基于这种思维，我们还能提出一系列有价值的问题。对开的《北京晚报》，一开的《人民日报》，八开的试卷，三十二开的笔记本，开数之间又有什么关系呢？把这些问题提出来、解答出来，这才是学习。如果学生掌握了这种思维方法，他们的学习就不再只是知识点的简单罗列了。

如何用自行车测量出自己家与学校的距离？这个测量需要知道车轮的周长，圆的周长＝直径×圆周率，在我们的教育下，学生对这个公式的记忆根深蒂固。但也正因如此，他们一味地只想着去量车轮的直径，量不出来，怎么办？一个平时很淘气的小男孩儿用粉笔在自行车外胎上画了一圈，再把自行车往前一推，有了印迹，周长就出来了，这才是真正解决问题的方法。再如测距离，学生每次测量的结果都不会一样，但每次的测量值都是对真实结果的一个逼近，而这种学习不在课本里。

如何为所在小区设计一个最佳的送奶路线、一个合理的保安巡逻路线？阅读和理解并非只存在于语文和英语这类科目中，送奶路线和巡逻路线的区别是什么？送奶要求用脚跑遍每一个楼洞，巡逻要求用眼睛看。“最佳”就是完成任务且走得最少。这种阅读和理解，学生只有真正去想、去做了，才能明白。

……

这样的过程、这样的应用联系了学生和教材的实际，好入手、有趣味、可深入。数学课堂中蕴含的不仅是数学，更是教育。从另一个角度来说，多一把尺子，就多一批好学生。有很多学生在奥数中碰得头破血流，也因此越来越讨厌数学，而在我们这样的过程、这样的应用中，发挥的是学生的个性和特长，能够给每个学生成功的体验,给每个学生发展的机会，学生会坚定不移地跟着老师执着地学习，这才是我们想要的。