经历过程比知道结果更重要——“三角形的内角和”一课的实践与思考

◇丁玉华

一 课前慎思

“三角形的内角和是180°”这一数学结论表述不足十个字，看似简单，实则蕴含着丰富的内涵，教起来却不易。教过“三角形的内角和”这一课的老师都会遭遇到这样的“尴尬”现象：

现象1：知其然，但知其所以然了吗？

由于部分学生在上课之前通过预习已经知道“三角形的内角和是180°”这个结论，在“量一量”验证的过程中，部分学生缺乏探究动机，在测量的过程中会反复调整数据，将测量的结果凑成180°，导致课堂上的探究活动流于形式。这是虚假操作还是面对误差时的理性“纠正”？

现象2：“量”有误差，“拼”与“折”也有缝隙！

学生很容易想到用“量”的方法探究三角形的内角和，但很难想到用“拼”或“折”的方法。在“量”“拼”“折”的过程中，有些学生不相信所有三角形的内角和都是180°，因为“量”有误差，就算是“拼”或“折”也有缝隙，更何况操作验证的三角形个数有限，使得“三角形的内角和是180°”这个结论“腰杆不硬”，不足以让人信服，课堂中的探究活动沦为一种摆设。

学生都“知道”了，课该怎么上？这是广大一线数学教师经常遇到、亟待解决的问题。其一，为何课堂上会出现如此“尴尬”的局面？教师该如何应对，才能激发学生的探究欲望，从而引导他们由质疑走向真探究，让探究真正发生、切实发展思维呢？其二，对于四年级学生而言，用“量”“拼”等操作方式验证三角形内角和的度数，是具有普遍性的基本方法，但是“不完全归纳”是唯一的验证办法吗？在具体的探究过程中，如何应用“不完全归纳法”体会其推理合情性的同时，辩证地认识到它的局限性，才能有助于培养学生思维的深刻性与缜密性？教学中该如何有效地培养学生的研究能力，让学生意识到当下结论归纳的“不完全”，并以此走上寻求尽可能“完全”的探究之路，让学生经历简单的论证过程来弥补中小衔接的断层呢？

二 课堂实践

1.创设问题情境，引发自主探究欲望。

（上课伊始，教师开门见山，直奔主题，板书课题）

师：关于三角形的内角和，你们已经知道了什么？

生：三角形的内角和是180°。

（全班学生没有一个不举手的，回答问题时还“得意洋洋”）

师：你们都认为是180°？（所有学生点头）我不信！这节课我们先来玩一玩“超级变变变”，考考你的眼力和思考力。

师：（课件先出示图1，接着出示图2）请看大屏幕，这两个三角形的内角和分别是多少度？

图1

图2

生：都是180°。

生：三角形不管什么形状，不管多大多小，内角和永远都是180°。

（全班学生依旧“自信满满”）

师：（出示图3）请继续看大屏幕，如果在下面的三角形中添一条线，将它们分开，现在这两个小三角形的内角和分别是多少度呢？

图3

（有的学生说90°，瞬间又改口说180°；也有学生说180°，但显然“口气不硬”了）

师：（出示图4）每个小三角形的内角和是多少度？把这两个小三角形拼成一个大三角形，所得大三角形的内角和是多少度？

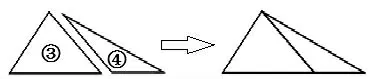
图4

（有的学生说360°，瞬间又改口说180°；也有学生说180°。显然犹豫不定）

师小结：一个大三角形的内角和是180°，分成两个小三角形，每个小三角形内角和还是180°吗？两个小三角形的内角和分别是180°，拼成一个大三角形，这个大三角形的内角和依然是180°吗？所有三角形的内角和都是180°吗？老师怀疑这个结论！你有什么办法说服我吗？

生：那就要想办法验证这个结论，说服老师。

生：老师，那我们量一量，算一算，看看到底是多少度……

思考：开课环节，教师挖掘数学特有的魅力，深入分析学生“已知”背后的“未知”，深度挖掘学生“想不到”的三个层次的“超级变变变”的导入方式，巧妙地将学生置身于问题情境中，激发学生的好奇心和探究欲望，将学生自然地引入到对新知的探究中。

2.留足探究空间，引导独立探究。

师：研究的方向很重要！你们认为应该测量计算哪几类三角形就能验证“三角形的内角和是180°”？

生：锐角三角形、钝角三角形、直角三角形。因为三角形按角分可以分成这三类，这样就可以包含所有的三角形了。

师：有道理！

（1）为什么我的三角形内角和不是180°？

师：好，接下来同桌合作验证，任意选择一个三角形，像这样先标出这个三角形的三个内角，然后一人量角，一人记录数据并计算。

（学生汇报三种三角形的测量结果和内角和，教师投影展示几种代表性情况。如图5）

图5

生：我有一个疑问，我也用了测量的方法，可是我测量出来的三个角和不是180°，这是怎么回事呀？

师：你真棒，敢于质疑。大家知道为什么吗？

生：我们测量角的度数时是有差异的，以前我们量角时就经常发生这种现象。

师：看来测量时会有些误差，我刚才发现个别小组一边量一边改数据，就想把内角和凑成180°。而大部分小组非常真实地记录下测量的数据！观察这些数据，你发现了什么？

生：都在180°左右！

师：那你根据结果能完全肯定三角形的内角和是180°吗？

（学生想了想，摇摇头）

师：我们通过测量的方法只能得到三角形的内角和大约为180°。那你们来评价一下，用测量的方法来验证存在什么问题？

生1：测量的时候会或多或少地产生偏差，所以会导致有不同的结果产生。

生2：直接量的方法虽然有误差，但也有一定的好处，至少让我们发现了三角形的内角和很接近180°。

（2）为什么我撕下来的三个角拼不成一个平角？

师：那究竟是不是180°呢？有没有避免误差的方法呢？

（学生陷入沉思）

师：刚才我们用的测量方法是把三个角的度数量出来再合并计算，会出现误差，那我们可不可以不测量，直接把三角形的三个角合并在一起呢？

生：（思考良久）老师，看到180°我联想到之前我们认识的平角。我有个办法，就是有点“残忍”，要把三角形的三个角剪下来拼一拼，看看拼出来的是不是一个平角。

师：能想到这个方法，真不简单！让我们一起试试看。

（大多数学生在剪角时，都是直直地剪下，由于剪之前没有对三角形的每个内角做上标记，导致大部分学生把剪下的“小三角形”转来转去，就是不能拼成一个平角。见此情境，教师组织学生汇报展示，互相学习）

师：针对这几种情况，剪和拼的时候需要注意什么？谁来给大家做个温馨提示？

生：先把三个内角分别标上序号，然后剪下来，剪的时候要保留每个内角的边和顶点，拼的时候要把角的顶点重合，边也要重合。

师：你怎么知道拼成的是平角？

生：我用直尺验证了，角的两边呈一条直线。

生：老师，我刚才发现把三角形的三个内角剪下来拼到一起时，角与角拼接后还有一点点缝隙。

师：把三角形的三个内角拼到一起组成了平角，但在操作的过程中也会有误差，比如角与角拼接时会有缝隙。

（3）为什么我的三角形三个内角折不到一起？

师：如果不想破坏这个三角形，还有什么方法能把三个内角拼到一起呢？

生：把三个内角折到一起。

（学生动手折）

师：在折的时候大家遇到了什么困难吗？

生：不太容易把三个顶点折到一起。

生：我折完以后三个内角之间还是有很大的缝隙！

（这句话引起了其他同学的共鸣）

（播放微课“原来这样折”，向学生介绍减少手工操作“误差”的两种折拼的方法）

方法1：准确地找到中位线，再进行对折的方法。（图略）

方法2：先找出三角形最长的一边，折出这条边上的高，找到对应的垂足；这个垂足就是最后拼成的平角的顶点。然后将三个内角的顶点分别对准垂足进行折叠。（图略）

思考：在本节课的探究活动中，面对学生在“量、剪拼、折”的过程中存在的误差，以及提出的疑问，我选择放手让学生充分经历“质疑—确信”的探究思考过程，促使学生从另一个角度体会了数学是一门严谨的学科，进而产生了对更完善的验证方法的好奇和渴望，为进一步用演绎推理的方法去探究验证埋下伏笔。

3.深入验证规律，激发学生理性思考。

师：前面大家采用量、剪、折的方法都不错，但在实际的操作中确实存在着一定的误差，我们能不能找到更加科学严谨、精确巧妙的证明方法呢？

（学生一时难以想到，都沉默不语）

师：（出示一个长方形）看到长方形，你想到了什么？

生：长方形的对边相等，四个内角都是直角。

师：今天我们研究“三角形的内角和”怎么会有长方形呢？

生：长方形可以分成两个直角三角形。

师：你们真厉害！下面请同学们在小组内讨论一下，能不能用它来证明三角形的内角和？

（小组讨论研究，教师巡视指导）

师：同学们，现在你有什么新的发现吗？

生：长方形的四个内角都是直角，长方形的四个内角的和一定是360°。把长方形沿对角线一分为二，就变成两个完全相同的直角三角形，每个直角三角形的内角和就是360°除以2等于180°。任意一个直角三角形都可以看作是由某个长方形剪开的，所以任意直角三角形的内角和一定是180°。

师：这个方法真是与众不同，看来用推理的方法能证明任意直角三角形的内角和是180°。

（教师用课件辅助，演示说明这一证明方法。图略）

师：在证明直角三角形的内角和一定是180°的基础上，现在你会验证锐角三角形、钝角三角形的内角和是180°吗？

生：我们组的方法正好可以解决这个问题，任何一个锐角三角形都可以沿高分为两个直角三角形，借用直角三角形的内角和是180°这个结论，两个直角三角形的内角和就是180°＋180°=360°，中间的两个直角不是大三角形的内角，所以锐角三角形的内角和就是360°－90°－90°=180°。同样的道理可以说明钝角三角形的内角和也是180°。

师：你们组能化未知为已知，真了不起！其他同学也是这个意思吗？

（教师用课件辅助演示上述证明过程。图略）

师小结：这种方法避免了在测量及剪拼过程中由于操作不当而出现的误差，能证明三角形的内角和是180°。我们进入中学以后，还将学习一种更加科学严谨的证明方法。

思考：三角形的内角和为什么是180°？中学数学中有严格的证明。从长方形的4个内角均为90°这一不容置疑的知识点出发，采取将一个长方形等分为两个完全相同直角三角形的方法，推导出直角三角形的内角和等于180°……有的教师认为这样的证明其实是在“循环论证”，但我认为这样处理，既重视在教学中对学生推理能力的培养，让学生经历从特殊到一般的思维历程，又有效渗透了演绎推理证明的数学思想，弥补中小衔接的断层。