推理，让数学课堂更显生机

◇陈李勇

人教版教材一年级下册“十几减5、4、3、2”一课，是在学生能熟练计算十几减9、8、7、6的基础上设计的，要求学生能用学过的方法完成十几减5、4、3、2的计算，同时体会“想加算减法”的优越性。

我在教学该内容时，在黑板上写了“12-5=？”，然后要求学生用自己认为最简单的方法计算。我预设学生会出现“破十法”“平十法”“想加算减法”等。在课堂上，也确实如我所料，学生很自然地提出上述三种方法，笔者引导学生对这三种方法进行了比较、优化。正当我以为这又会是一节平淡的计算课的时候，有学生突然站起来说：“老师，我有更简便的方法。”出于对生成的敏感性，

我让她继续说下去。“12-5，可以把被减数个位上的2和减数5加起来，答案就是7。”

听完她的介绍，我转身问其他学生：“她说的你们听得懂吗？你们觉得这是规律还是巧合呢？”孩子表示听得懂，而且一致认为是规律。我又问：“就凭这么一个算式，就能得出这是规律吗？”有学生提出：可以再举几个例子。我想：太好了，就等你们进我的圈套呢。于是，我在黑板上写下13-5、14-5、15-5……让学生计算。他们发现刚才的“规律”果然正确。我看时机已成熟，又写下13-6、14-7让他们计算。部分学生没反应过来，还用刚才的“规律”解决。当大家发现答案有误时，正是他们的“愤悱”之际，我引导学生思考：你有什么发现？不一会儿，一个学生站起来说：“只有当减数是5时规律才成立，因为10可以分成5和5，所以5+2=7。”根据他的表述，我顺势在黑板上写下这样的式子，如图1。

最后，我总结道：“有的规律只能在一定的范围内运用，超出这个范围，规律也就不存在了。并且，有时候用规律不一定就能带来方便，比如计算18-5，还是一般方法更快。”我想，让一年级的孩子经历观察、猜想、验证、修正、发现的过程，是可行的。

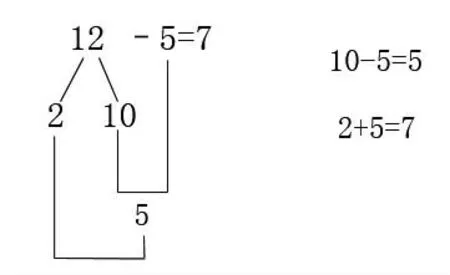
图1