剩之愈小，分之弥细——“精打细算”教学思考

◇董文彬

课前慎思

“精打细算（小数除以整数）”一课是北师大版教材五年级上册第一单元“小数除法”的第一课。在学习本课之前，学生已经学习了除法的意义和整数除法，认识了小数的意义、小数加减法、小数乘法。这些内容为学生学习小数除法提供了知识基础和活动经验（包括操作的经验和思维的经验），成为本课教学的起点。

笔者对同一位教师任教的两个班学生进行了前测（问卷、追访），以探寻学生真实的思维路径。其中，A班题目为:10.2÷3等于多少？请想办法解决，尽可能详细地记录下你的思考过程。B班题目为:买3袋奶一共花10.2元，每袋奶多少元？可以利用学具研究，并尽可能详细地记录下你的思考过程。

调研结果显示：面对问题，学生由起初的“不知道”到最终的“我会做”，有两个阶段需要经历和跨越:其一,整数部分剩余的“1”和小数部分的“2”组成新的数后“还能分吗”？这是学生认识和理解上的“难点”。其二，商中的小数点怎么办？这是学生思维陷入纠结的“结点”。

A班有62.5%、B班有85%的学生，在答卷中体现出“我会做”，竖式书写完全正确，但追访之后发现学生“会做”但不一定“能懂”。另外，提供模型学具的B班比不提供模型学具的A班，学生的理解情况要好得多。可见，直观模型对促进学生理解算理有很大帮助。

基于以上的分析与思考，笔者设计了以下学习目标：

1.在具体的情境中研究小数除法，沟通“元”“角”“分”与计数单位间的联系，感悟小数除法的意义。

2.借助直观模型，经历探索小数除以整数的计算过程，掌握小数除法的计算方法，感悟方法背后的道理。

3.创设观察、操作、思考、交流的空间，激发自主研究问题的热情。

课中践行

一、情境聚焦，提出问题

出示课本情境图：（如图1）

图1

师：仔细观察大屏幕，从图中你发现了哪些数学信息？

生：在甲商店买了5包牛奶，一共花了11.5元，在乙商店买了6包，一共花了12.6元。

生：我还发现两个商店牛奶的包装规格是完全一样的。

师：根据这些数学信息，请你提出一个数学问题。

生：哪家商店的牛奶便宜？

师：该怎么解决这个问题呢？

生：需要算一算这两家店每包牛奶分别是多少元。

生：就是要先计算出牛奶的单价，再进行比较。

师：我们先来算一算“甲商店牛奶每包多少元”，该怎么列式呢？

生：要用除法来计算，算式是11.5÷5。

师：为什么用除法解决？

生：单价=总价÷数量。

生：求甲商店牛奶每包多少元，就是要把总钱数11.5元平均分给5包牛奶，所以用除法解决。

二、借助模型，自主探究

1.独立探索。

师：（指11.5÷5）观察这个算式，和以往学习的除法算式有什么不同？

生：以前学习的被除数和除数都是整数，这道题的被除数是小数。

生：这道算式是小数除以整数。

师：根据你的知识和经验想办法算出它的结果，必要时可借助提供的学具分一分、摆一摆，详细写出你的思考过程。

（生操作、计算，师巡视指导，收集学生的典型算法后进行交流）

2.模型说理。

（先呈现学生的4种算法。如图2）

图2

师：黑板上展示了大家比较典型的4种算法，你能读懂他们的想法吗？

生1：方法①是先把11.5元换算成115角，然后用竖式计算115角除以5得23角，再把23角换算成2.3元。大家有问题吗？

生2：为什么要把11.5元换算成115角？

生1：因为被除数是小数，把11.5元换算成115角，被除数就变成整数了，这样比较好算，算完后再把结果的单位“角”换算回“元”就可以了。

师：遇到新问题，想办法把它转变为以前学过的知识再加以解决，这种方法在数学上叫作“转化”。

生2：我还想给你提个建议，你的竖式没有写完，需要写完整。

（生接受，并进行修改）

生3：方法②是先把11.5乘10得115，用115÷5得23，再把23除以10得2.3，所以11.5÷5的结果就是2.3。

生：方法①和方法②差不多，也是把被除数转化为整数计算，再把结果变回去。

生：不同点是方法②用到了商的变化规律，方法①是借助元和角的关系换算转化的。

师：非常清楚的解释！我们再来看后两种。

生：方法③是先把11.5元写成10元＋1.5元，先用10元除以5得2元，再把1.5元换算成15角，用15角除以5得3角，然后把3角换算成0.3元，最后2元加0.3元得2.3元。

生：我明白了，他是先分整元的钱，再分剩下的，分剩下的钱时为方便计算也用到了转化。

生：方法④和方法③差不多，把11.5写成10加1.5，先用10除以5得2……

生：为什么要把11.5写成10加1.5来算？

生：10除以5，1.5除以5都好算。

生：1.5÷5被除数也是小数，怎么算出0.3？

生：可以反着想，几乘5得1.5。

师：除此以外，还有同学用到了竖式计算的方法，我们一起来看一看。

（呈现以下3种竖式记录方式。如图3）

图3

师：仔细观察这3个竖式，你能发现并提出什么问题？

生：竖式①和竖式③商中间都有小数点，竖式②商中间没有，这个小数点要不要点？

生：肯定要点啊，要是不点商就变成23了，肯定不对。

生：竖式①15中间点了小数点，竖式②和竖式③没点，15中间的小数点点吗？

生：点。

生：不点。

生：我觉得点不点好像都对。

生：我觉得这3个竖式只有③是对的，我在课外班上学过，这是标准的竖式计算方法。

师：刚才同学们提出的这两个问题都很重要。我们请竖式的主人说一说用竖式是怎么除的，说清楚每一步的意思。

生1：11.5除以5，我先用11除以5，商2写在个位“1”上面；2乘5得10,11减10余1；再把5落下来，用15除以5，商3写在十分位“5”上面，3乘5得15,15减15得0，除尽，最后结果就是2.3。大家听懂我的方法了吗？有什么问题吗？

生2：（指商2.3中的小数点）小数点为什么点这儿？

生1：我觉得被除数有小数点，商也应该有，商的小数点应该和被除数的小数点对齐。

生3：这里的1.5是什么意思？

生1：我不太清楚。

师：能否从除法“平均分”的角度考虑呢？

生4：（借助元、角人民币学具）我摆好11个1元和5个1角表示11.5元，竖式中先用11除以5，就是把11元平均分成5份，每份分得2元，商2写在个位上；2元乘5得10元，说明分走10元，11减10余1，还剩下1元；把十分位的5落下来，这个5表示5角，和前面剩下的1元组成1.5元；1.5元平均分成5份不好分，于是把1元换成10个1角，和5角加起来一共是15角，现接着平均分成5份，每份得3角，商3写在十分位。这样最后每份是2元3角，也就是2.3元，商中间的小数点必须点，而且必须和被除数的小数点对齐。大家听懂了吗？

生3：我还是不明白15中间的小数点到底要不要点。

生5：我认为不用点，因为1表示整数部分分剩下的1元，5表示5角，单个的1元不能直接平均分成5份，需要把它转换成10角，和5角加起来是15角，再接着分。这里的1.5元已经转化为15角，所以15中间的小数点不用点。

生3：我听懂了，也就是说整数部分余下1元后，不能继续分，需要把它变成10角，加上还有的5角，这样第二次的被除数实际上表示15角，而不是1.5元，所以15中间不用点小数点。

师：还有其他的解释吗？

生6：我是借助正方形模型来分的。先摆出11个正方形表示11个1，再把1个正方形平均分成10条，其中的5条表示0.5，这样11个正方形和5条就表示11.5。先分11个正方形，平均分成5份，每份是2个，还剩下1个正方形，在竖式中就是用11除以5，商2写在个位上，11减10还余下1个1。余下的这个1不能直接分，需要把它（1个正方形）平均分成10条，和那5条组成15条，再接着分，平均分成5份，每份是3条，也就是0.3，这样最后每份就是2.3。大家听懂我的解释了吗？有什么问题吗？

师：（指余数1）这里的1表示什么？

生6：1表示整数部分第一次除完后余下的1个1。

师：这里的5表示什么？

生6：5表示5个0.1。

师：这里的15又表示什么？

生6：15表示15个0.1。

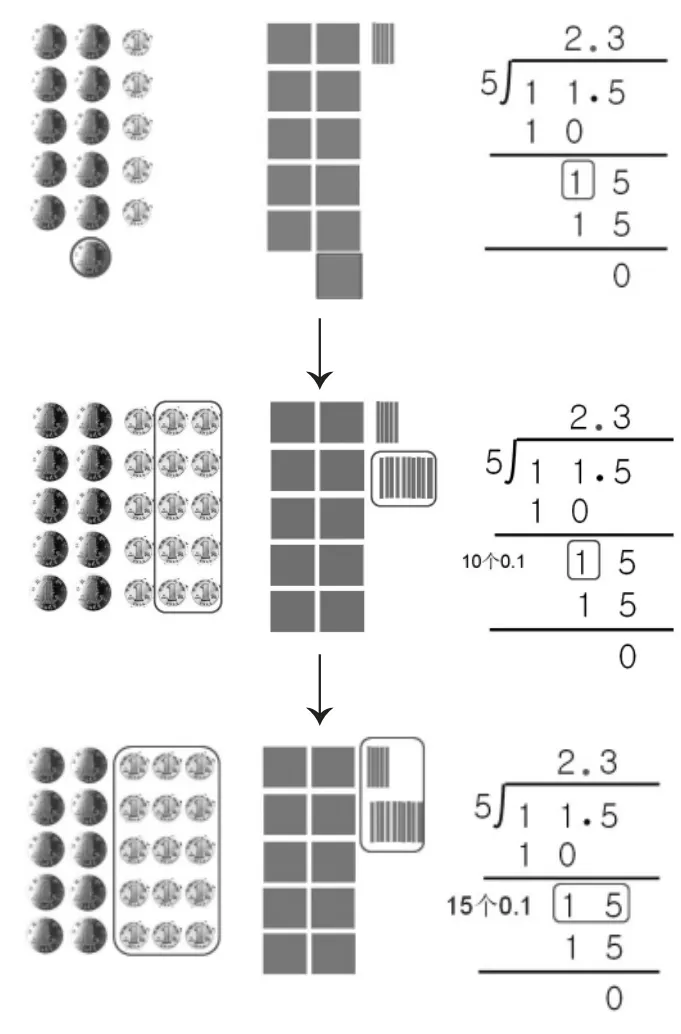
图4

师：我还是不太明白，这里的1表示1个1，5表示5个0.1,合在一起表示1.5才对呀，15怎么就表示15个0.1了？

生6：因为剩下的1个正方形不能直接分了，需要把它再平均分成10条，才能与那5条一起接着分。

生6：整数部分余下的1不够除，需要把它转换成10个0.1，这样就和这5个0.1统一了，变成15个0.1，再接着除下去。

生1：我有点懂你的意思了，把余数1转换成10个0.1后，第二次的被除数表示15个0.1，所以15中间不用点小数点，15个0.1接着除，每份得3个0.1。

生2：我明白了为什么商中间要点小数点，而且要和被除数的小数点对齐了！

生2：第一次除得的商2表示2个1，需要写在个位上，第二次除得的商3表示3个0.1，需要写在十分位上，个位和十分位之间必须用小数点隔开。

3.沟通联系。

（课件同步演示人民币实物、模型、竖式中对余数“1”“15”关键步骤的理解。如图4）

师：回顾刚才大家借助学具摆、分的过程，竖式中被除数的整数部分除完后，个位上余下的“1”表示什么？在前两幅图中能找到吗？

生：这个“1”表示被除数的整数部分除完后个位上余下1个“1”，在第一幅图中就是11元分走10元后剩下的1元，在第二幅图中就是11个正方形分走10个后还剩下的1个正方形。

师：为了能继续除下去，需要做什么事？

生：把剩下的1元换成10个1角，和那没分的5个1角组在一起是15个1角。

生：把剩下的1个正方形再平均分成10条，和那没分的5个1条组在一起是15个1条。

师：也就是要把这个“1”转化成什么？

生：10个0.1。

师：这里的15表示什么？

生：15个1角。

生：15个1条。

生：15个0.1。

师：用15个0.1再继续除以5，每份得多少？

生：3个0.1。

生：这样解释我更加清楚了，第二次除得的商应写在十分位上，商中间要点上小数点，把2个1和3个0.1隔开。

三、巩固内化，延伸拓展

1.解决乙商店牛奶的单价，体会被除数整数部分除尽的情况，并进行比较，得知乙商店的牛奶便宜。（过程略）

2.学生独立完成题目（如图5），体会除数是两位整数的情况。（过程略）

3.学生填写并解释（如图6），体会对竖式的过程性理解。（过程略）

图5

图6

四、回顾历程，归纳总结

师：回顾这节课的学习，你有什么收获？相比整数除法，你对小数除法运算有了哪些深刻感受？

生：我不仅学会了怎么用竖式计算小数除法，还明白了除的过程中每一步的意思。

生：我发现被除数整数部分的除法就是整数除法，关键是算商的小数部分，道理和整数除法是一样的。

生：通过分、摆学具，我明白了整数部分余下的“1”为什么要看成10个0.1再接着除了。

……

生：高一级的计数单位不够除时，要把它转化成低一级的（计数单位）继续除！

师：你们的收获我也深有同感！谢谢同学们的积极探索。