基于模型的冗余驱动并联机构神经网络同步协调控制

刘晓飞 姚建涛 赵永生

(1.燕山大学先进锻压成形技术与科学教育部重点实验室, 秦皇岛 066004；2.燕山大学河北省并联机器人与机电系统实验室， 秦皇岛 066004)

0 引言

冗余驱动可以增加并联机构有效工作空间[1-3]，改善机构动力学特性[4-6]，以及提高机构刚度、增加承载力[7-8]、消除关节间隙[8-10]等。虽然冗余驱动并联机构具有很多优点，但要实现这些优点，还要依赖于控制方法。GANOVSKI等[11]采用基于反馈计算力矩控制法对分段冗余驱动并联机构进行控制。CHAKRAOV[12]采用刚度控制策略对冗余驱动并联机构进行控制。CHENG等[13]对比分析了关节空间PD控制、广义坐标系PD控制、增广PD控制以及计算力矩控制4种控制方法。SHANG等[14-16]设计了自适应计算力矩控制、工作空间协调运动控制和鲁棒非线性控制3种方法。NIU等[17-18]采用滑模控制方法对平面冗余驱动机构进行了控制。MULLER等[19]提出了一种基于冗余坐标系计算力矩控制和增广PD控制策略。LAMAURY等[20]基于关节空间的双环反馈对绳索机构进行了控制。崔学良等[21]将鲁棒轨迹跟踪和目标阻抗控制结合，实现了冗余驱动并联机构的柔顺性控制。WU等[22-23]采用力位混合驱动方法实现了冗余驱动机构的控制，并设计了动力学补偿器[24]提高位置控制精度。这些方法都是对各关节驱动力分别进行控制的，并没有考虑冗余驱动机构驱动力间的协调约束关系。对于多驱动间的同步协调控制[25]，目前主要集中于轨迹跟踪控制，暂未涉及驱动力间的同步协调控制。

针对冗余驱动并联机构的驱动协调性问题，本文提出一种基于模型的神经网络驱动力同步协调控制方法。以6PUS+UPU冗余驱动并联机构为对象，推导机构动力学模型；在力位混合驱动模式的基础上，提出一种驱动力同步协调控制策略，结合神经网络设计协调控制算法；利用软件仿真与样机实验分别对所提出的控制方法进行验证。以期所提出的控制方法为冗余驱动并联机构的控制应用提供新的思路。

1 机构简介与动力学建模

1.1 并联机构6PUS+UPU简介

冗余驱动并联机构6PUS+UPU的结构简图如图1所示。该机构包括6个PUS分支、1个UPU分支、动平台以及机架组成，其中PUS分支为驱动分支，UPU分支为约束分支。PUS由滑块与定长连杆组成，滑块由伺服电机驱动并沿导轨作垂直于水平面的上下移动，定长连杆通过球铰与动平台相连接，滑块与连杆之间通过虎克铰连接。UPU分支包含2个由P副连接的定长连杆，2个连杆均通过虎克铰分别与机架和动平台相连接。基于文献[26]对该机构自由度的分析，该机构的6个PUS驱动分支对动平台施加6个线性无关的驱动，中间UPU约束分支对动平台施加1个绕分支轴线方向的转动约束，故该机构为5自由度冗余驱动并联机构，其冗余度为1。冗余度是指机构驱动数目超过机构自由度的数目。

图1 并联机构6PUS+UPU结构简图Fig.1 Diagram of parallel manipulator 6PUS+UPU

机构动平台在空间中的位置向量可表示为p=(x,y,z)T，而姿态矩阵可以表示为R=R(x,α)R(y,β)R(z,γ)，因此动平台在空间中的位姿可用由6个位姿参数组成的广义坐标q=(x,y,z,α,β,γ)T表述。对于5自由度并联机构6PUS+UPU而言，广义坐标的6个参数中只有5个参数为独立变量，取qs=(x,y,z,α,β)T，记为独立广义坐标。机构在广义坐标与独立广义坐标下的速度与加速度间的映射关系为

(1)

(2)

1.2 机构动力学建模与驱动力分配

机构动力学模型是对机构进行动力学分析与研究的基础。为了便于模型推导与分析，基于文献[27-28]对6PUS+UPU机构的运动学分析，利用虚功原理建立冗余驱动并联机构的动力学模型。为了简化运算，忽略各关节摩擦力对机构动力学的影响。

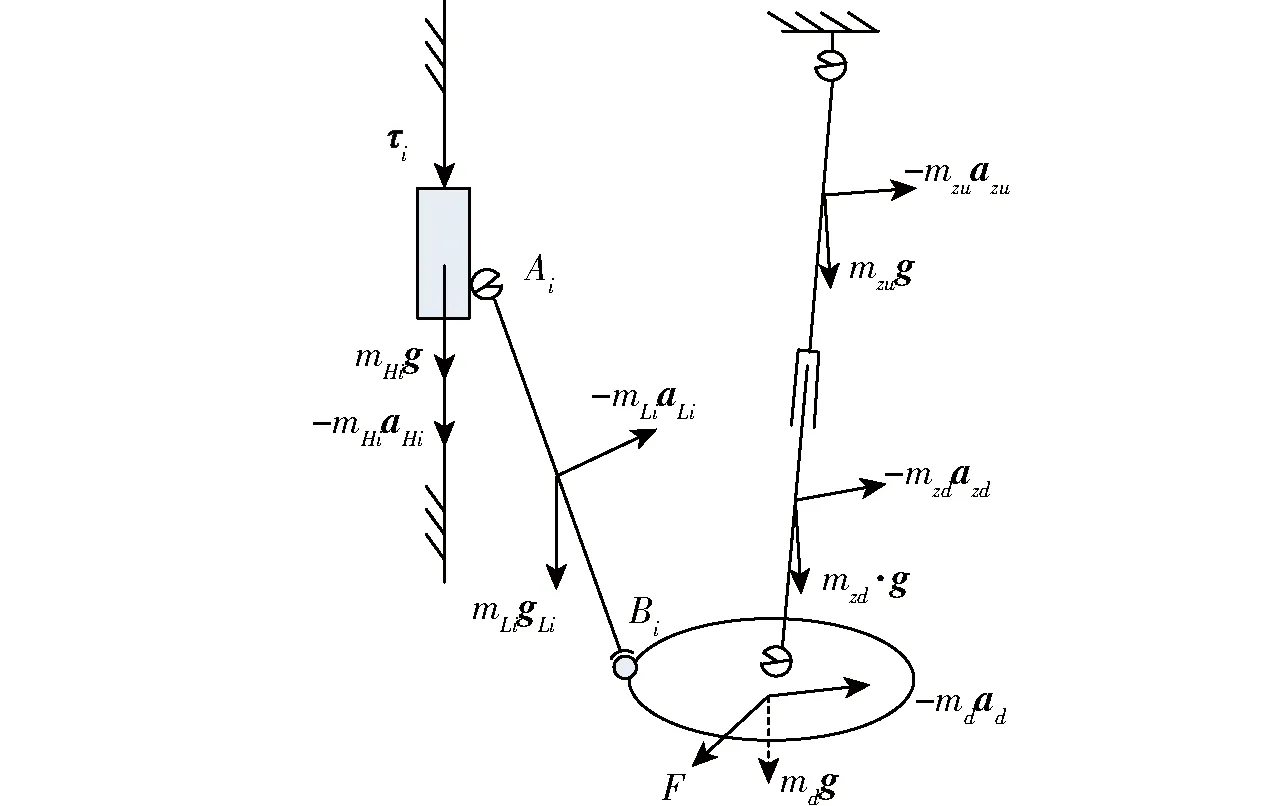
图2 并联机构6PUS+UPU受力分析Fig.2 Force analysis of manipulator 6PUS+UPU

机构在运动过程中主要受重力、惯性力以及外负载等的影响，建立机构的受力平衡方程，可以获得机构的动力学模型，并对机构的驱动力进行求解。冗余驱动并联机构6PUS+UPU的受力分析如图2所示，其中τi∈R6×1为驱动分支滑块所受驱动力，g∈R6×1为重力加速度，ai∈R6×1为各构件广义加速度(包含移动加速度与转动加速度)，mHig与mLig、-mHiaHi与-mLiaLi分别为驱动分支滑块和连杆所受重力与广义惯性力，mzug与mzdg、-mzuazu与-mzdazd分别为约束分支上下连杆所受重力与广义惯性力，mdg与-mdad分别为动平台所受重力与广义惯性力，F∈R6×1为动平台所受负载。

在笛卡尔坐标系下，假定机构动平台的广义运动速度(包括线速度与角速度)为υd∈R6×1，中间约束分支上下连杆的广义运动速度分别为υzu∈R6×1和υzd∈R6×1，连杆AiBi的广义运动速度为υLi∈R6×1，滑块的广义运动速度为υHi∈R6×1，这些构件在广义坐标系q下的速度雅可比矩阵分别为Jd∈R6×6、Jzu∈R6×6、Jzd∈R6×6、JLi∈R6×6和JHi∈R6×6，于是可得

(3)

对于6PUS+UPU并联机构而言，各驱动关节均为单自由度关节，因此其驱动关节的驱动力可以简化为标量。记各驱动分支P副的单位方向向量为ni∈R6×1，滑块所受驱动力幅值为τi∈R，于是可得

τi=niτi

(4)

基于虚功原理，机构承受的所有外力的作用，经过虚位移所作的虚功，总和等于零。建立6PUS+UPU并联机构的虚功平衡方程，即

(5)

将式(3)、(4)代入式(5)，可整理得

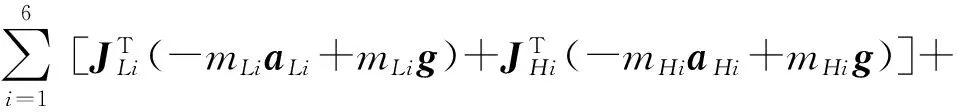
(6)

通过参数分离，可以将机构各运动构件在广义坐标q下的广义惯性力分解为

(7)

于是式(6)可进一步整理得到

(8)

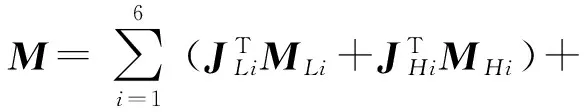
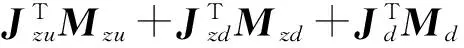
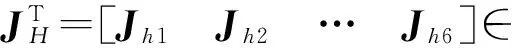
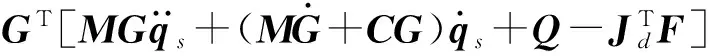
(9)

式(9)即为冗余驱动并联机构6PUS+UPU在独立广义坐标qs下动力学平衡方程，其中JHG∈R6×5为机构在独立广义坐标qs下的速度雅可比矩阵。对于并联机构6PUS+UPU而言，由于中间分支运动约束的原因，机构具有5个自由度，因此其在广义独立坐标下的速度雅可比矩阵的秩为5，即rank(JAG)=5。由于机构驱动力向量中τH包含6个待求解量，因此式(9)不能获得驱动力的唯一解。对于冗余驱动机构驱动力的求解，最多的是使用伪逆的方法，即

(10)

式中 (JHG)+T——矩阵(JHG)T的广义伪逆

2 冗余驱动机构的驱动力同步协调控制

2.1 驱动力同步协调控制策略

对于冗余驱动并联机构而言，基于关节空间的力位混合驱动是一种有效的控制方式，可以在控制机构运动轨迹的同时，主动调节机构的驱动力输入，实现对机构驱动力的优化分配，进而优化机构受力状态。文献[23，26]证明了该方法的有效性。然而，基于关节空间的控制模式下，控制系统对机构各关节的控制相对独立，缺乏相互之间的协调。对于串联机构以及非冗余并联机构而言，较低的关节协调性只会造成机构轨迹误差；但对于冗余驱动并联机构而言，较低的驱动协调性容易引起较大的机构内力，降低机构精度与力学性能，甚至造成机构过度磨损与破坏。

为了提高冗余驱动机构各关节的驱动协调性，可以设计同步控制器，根据各关节驱动的实时状态进行驱动调整。6PUS+UPU机构基于同步控制器的驱动力同步控制策略如图3所示，在机构动平台轨迹规划的基础上，通过机构逆运动学计算非冗余驱动关节的轨迹输入，通过逆动力学计算冗余驱动关节的驱动力输入，然后通过驱动系统实现对冗余驱动机构运动位置控制与受力状态的调整。同步控制器根据位置驱动关节驱动力误差来调整力驱动关节驱动力输入，进而提高冗余驱动机构各驱动关节间的驱动协调性。

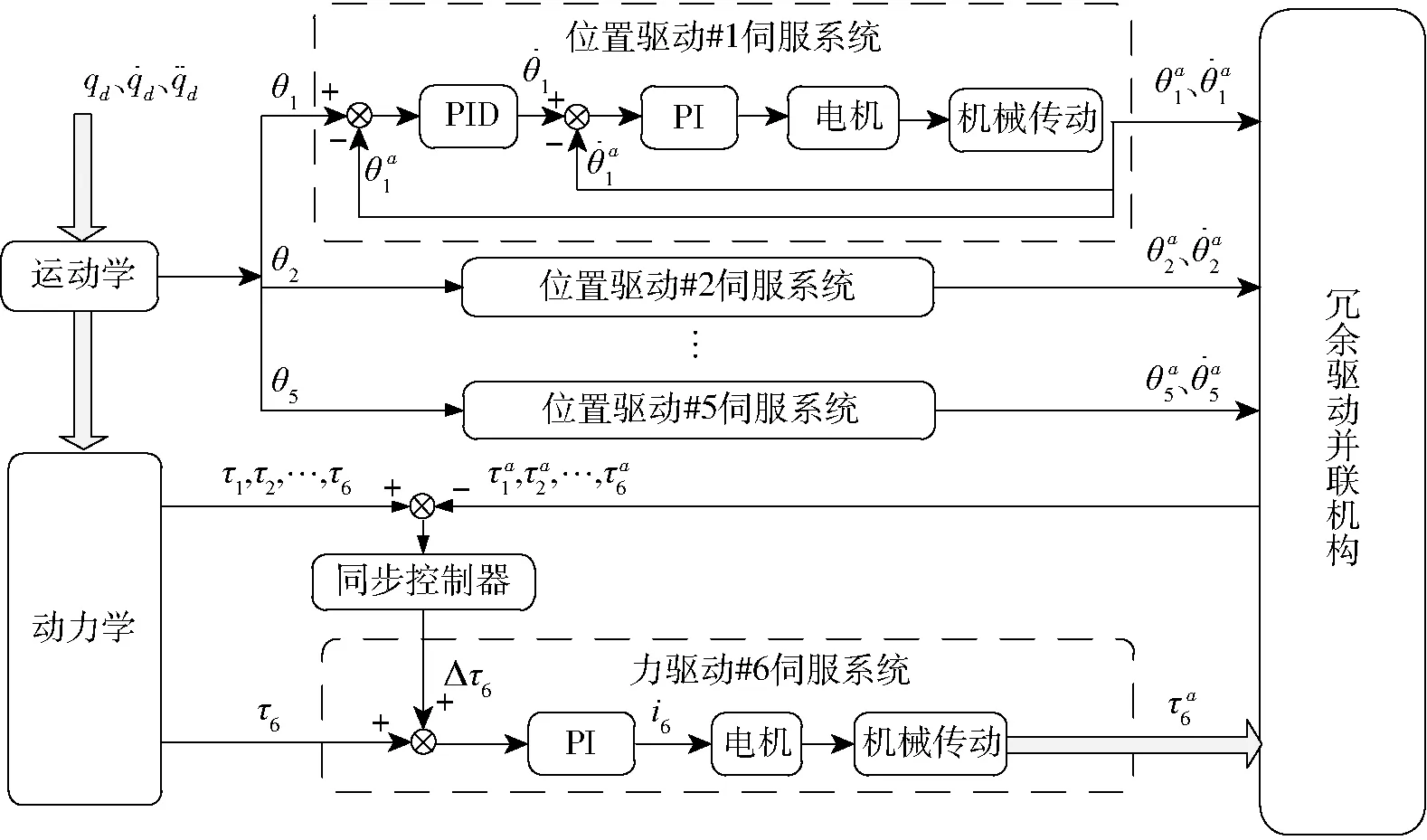
图3 驱动力同步协调控制框图Fig.3 Block diagram of driving force synchronous control

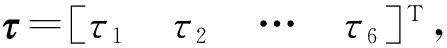
e=τ-τa

(11)

式中e——分支驱动力误差

基于冗余驱动机构各驱动关节驱动力误差可以计算冗余驱动力τ6的实时调节量，即

Δτ6=λTe

(12)

其中

式中λ——关节驱动力误差计算权重

λi可根据控制系统的实际控制精度进行调整。

2.2 神经网络同步控制

本节设计神经网络控制器，根据6个驱动分支驱动力的控制误差来计算同步控制器中的6个权重参数，进而改变冗余驱动分支力的实时调整，提高各分支驱动协调性。

2.2.1神经网络控制器设计

神经网络控制器采用3层神经网络结构，如图4所示，其输入变量为6个驱动分支的驱动力误差e，输出变量为同步控制器中的误差权重λ。

图4 神经网络框图Fig.4 Diagram of neural network

基于神经网络的同步控制器加权系数λ的计算结果可以表示为

λ=φo[woφh(whe)]

(13)

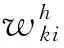
(14)

(15)

其中

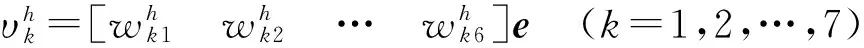
yh——隐含层节点的输出结果向量

2.2.2神经网络的自学习

利用神经网络的误差反射传播自学习算法，可以优化同步控制器的控制参数，进而提高冗余分支闭环系统对内力的控制精度。定义用于评价闭环系统对分支内力控制精度的评价函数

(16)

基于评价函数的负梯度可以实现对神经网络加权系数的调整，即输出层节点与隐含层节点的输入加权系数调整算法分别为

(17)

(18)

式中η——神经网络学习效率，可人为进行调整

基于偏微分理论，式(17)、(18)可进一步简化为

(19)

(20)

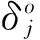
(21)

其中

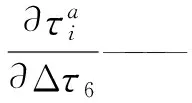
将式(11)、(12)、(14)、(16)代入式(21)，可进一步得到

(22)

利用神经网络的误差反射传播自学习算法，隐含层神经元的局域梯度为

(23)

2.3 动力学模型应用

对于位置驱动而言，其控制规律基于关节轨迹误差反馈，实际驱动力由关节受力状态决定；对于力/力矩驱动关节而言，可以主动改变关节驱动力或力矩的输入。因此对于处于力位混合驱动模式下的冗余驱动并联机构而言，可以通过主动改变冗余分支的驱动力输入来改变机构驱动力的实时分配。

式(8)可改变为

(24)

式(24)进一步整理可得

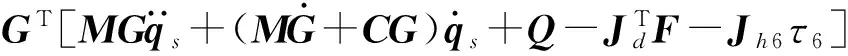
(25)

其中

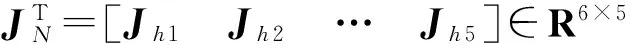
JNG∈R5×5为机构在独立广义坐标qs下非冗余驱动部分滑块的速度雅可比矩阵，当其处于非奇异位姿时，该矩阵可逆。于是可以得到非冗余驱动分支驱动力的唯一解，即

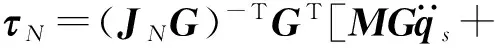
(26)

式(26)为满足预定轨迹与负载情况下冗余驱动并联机构冗余驱动力与非冗余驱动力间的约束关系，通过对冗余驱动力的改变实现对非冗余驱动力的调节。

当#6驱动关节驱动力存在调整量Δτ6时， #1～#5驱动关节的实际驱动力输入为

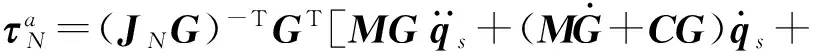
(27)

基于偏微分理念，可以获得

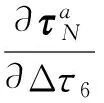
(28)

式(28)即为6PUS+UPU机构实际驱动力向量与冗余驱动力调整量间的偏微分映射关系，可进一步表示为

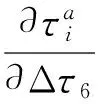
(29)

式中 [(JNG)-TGTJh6]i——向量[(JNG)-T·GTJh6]∈R5×1的第i个元素

因此式(21)中ki的计算结果为

(30)

3 仿真验证

以冗余驱动并联机构6PUS+UPU为对象，通过建立混合仿真模型，验证上述控制方法的有效性。利用Matlab软件的Simulink建立控制系统的仿真模型，利用ADAMS建立机构的动力学仿真模型，将两者结合，建立包含机构本体与控制系统的机电一体化系统仿真模型，进而可以对控制系统的相关性能进行分析。并联机构6PUS+UPU相关几何参数如表1所示，相关的惯性参数如表2所示，表2中转动惯量分别表示构件绕自身3个惯性主轴的转动惯量。机构动力学仿真模型如图5所示。

表1 6PUS+UPU机构几何参数Tab.1 Geometrical parameter of manipulator 6PUS+UPU

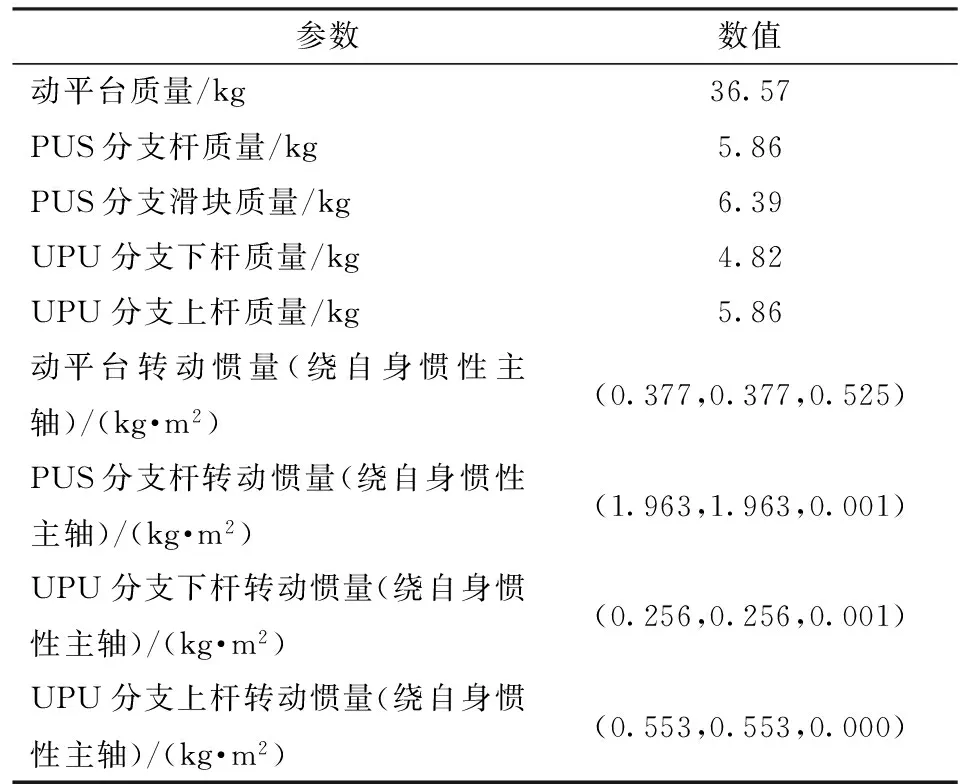
表2 6PUS+UPU机构惯性参数Tab.2 Inertial parameter of manipulator 6PUS+UPU

图5 机构6PUS+UPU动力学仿真模型Fig.5 Simulation model of manipulator 6PUS+UPU

仿真过程中，动平台沿初始位姿所在平面作的圆周运动，圆周半径为0.10 m，圆心为动坐标系原点OB，运动完一周的时间为15 s，运动过程中动平台姿态不发生改变。对于该并联机构而言，UPS驱动分支对动平台不产生运动约束，而中间UPU约束分支只约束动平台沿约束分支轴线方向的转动，因此该实验中的运动轨迹上，机构不存在奇异位形。

基于运动学计算#1～#5分支滑块的期望运动轨迹，并由位置驱动系统控制滑块的实际运动；基于动力学计算#6分支滑块所需要的期望驱动力，并由力驱动系统控制滑块的驱动力输入。分别采用传统的力位混合驱动和驱动力同步协调控制两种方法对并联机构进行控制，并记录运动过程中伺服驱动系统实际施加于各驱动分支滑块上的驱动力。基于最小二乘法计算冗余驱动并联机构6PUS+UPU的期望驱动力优化分配，其结果如图6所示；采用传统力位混合驱动方法的伺服系统施加于滑块的实际驱动力如图7所示，其与期望驱动力间的偏差如图8所示；采用驱动力同步协调控制方法的伺服系统施加于滑块的实际驱动力如图9所示，其与期望驱动力间的偏差如图10所示。

图6 期望驱动力优化分配Fig.6 Expected driving force distribution

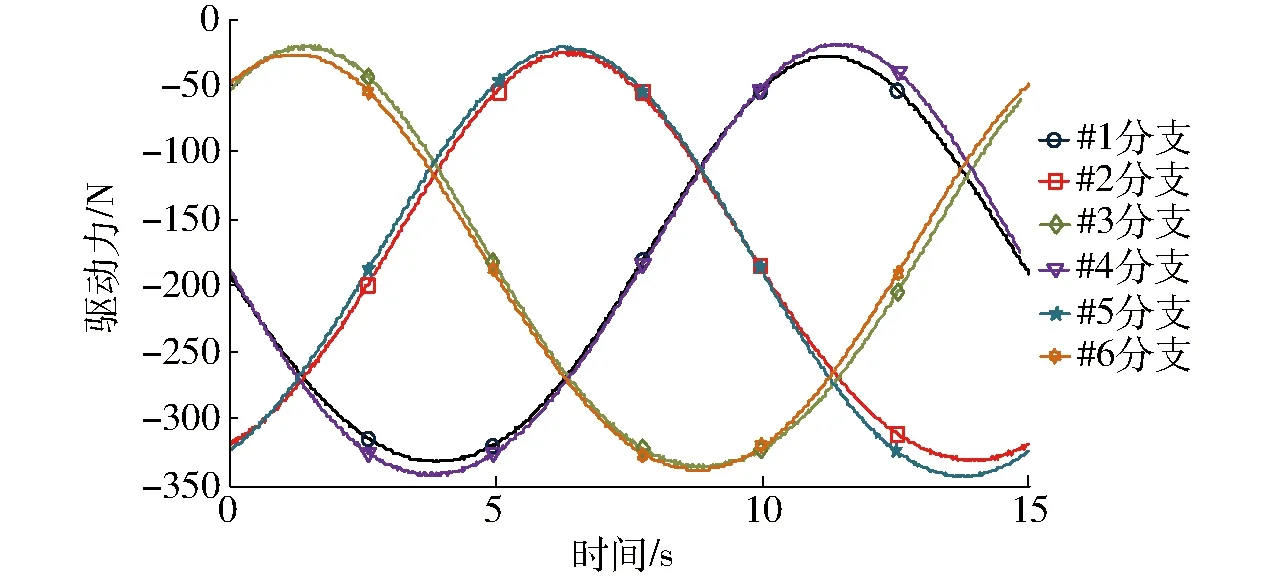
图7 力位混合驱动实际驱动力Fig.7 Actual driving force distribution of force-position hybrid actuation

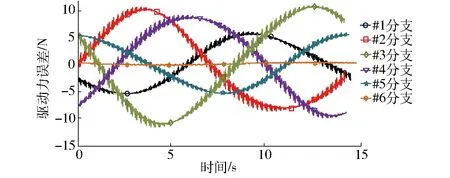
图8 力位混合驱动实际驱动力误差Fig.8 Driving force error of force-position hybrid actuation

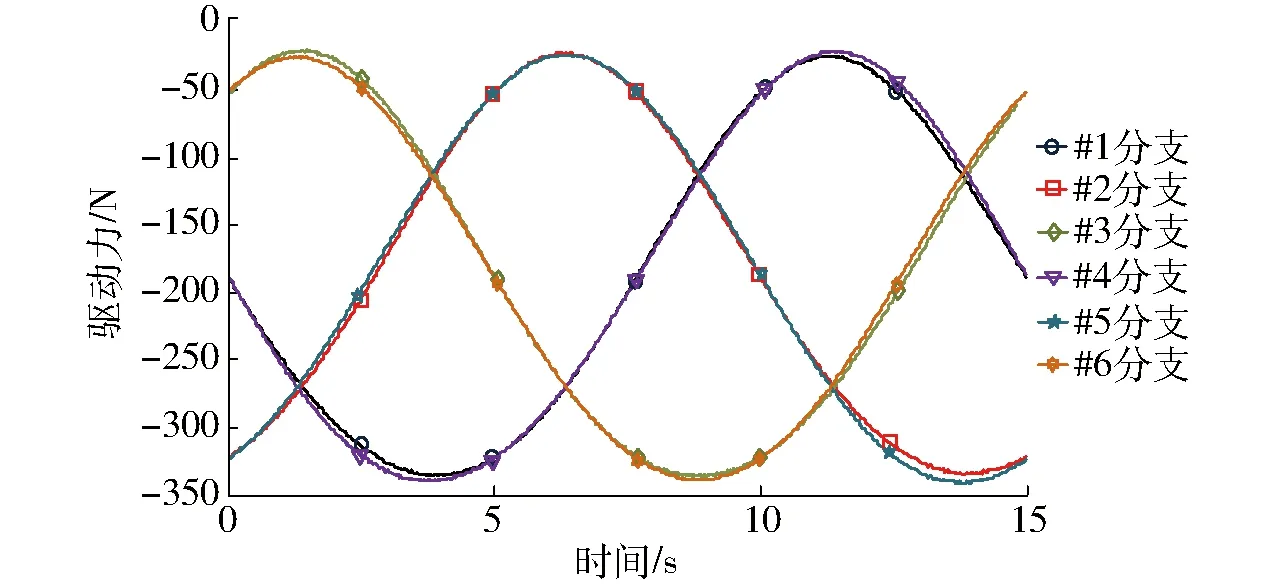
图9 驱动力同步协调控制实际驱动力Fig.9 Actual driving force distribution of driving force synchronous control

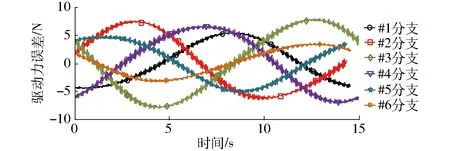
图10 驱动力同步协调控制实际驱动力误差Fig.10 Driving force error of driving force synchronous control

由图6、7、9可得，力位混合驱动模式下，驱动系统施加于各分支滑块的实际驱动力与期望驱动力基本相同，但仍然存在一定的偏差，说明该控制方式对冗余驱动并联机构而言确定是一种有效的控制方式，但控制精度有待进一步提高。由图8和图10可得，较传统力位混合驱动方式而言，驱动力同步协调控制方式下的位置驱动关节驱动力误差要明显减小，力驱动关节的驱动力误差有所增大，但各驱动分支间的驱动力误差较均匀，且整体变化范围小于传统力位混合驱动模式下的驱动力误差。这说明驱动力同步协调控制可以有效提高各驱动关节间的驱动协调性。

4 样机实验

冗余驱动并联机构6PUS+UPU样机如图11所示，其相关几何参数和惯性参数如表1与表2所示。该样机基于PMAC控制卡搭建其控制系统，#1～#5分支驱动电动机采用位置驱动模式，#6分支驱动电机采用力矩驱动模式。

实验过程中，样机完成与上节仿真过程中相同的运动轨迹，并分别采用传统的力位混合驱动和驱动力同步协调控制两种方法对并联机构进行控制，记录运动过程中伺服驱动系统实际施加于各驱动分支滑块上的驱动力，并计算其与期望驱动力间的误差。采用传统力位混合驱动方式下样机的实际驱动力如图12所示，采用驱动力同步协调控制方式下的实际驱动力如图13所示。图14表示两种控制模式下各分支实际驱动力与期望驱动力间的最大误差，包括正向误差与负向误差；图15表示两种控制模式下实际驱动力与期望驱动力间的平均误差，包括正向误差与负向误差。

图11 并联机构6PUS+UPU样机Fig.11 Prototype of parallel manipulator 6PUS+UPU

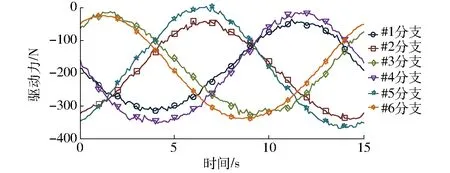
图12 力位混合驱动下各分支实际驱动力Fig.12 Actual driving force distribution of force-position hybrid actuation

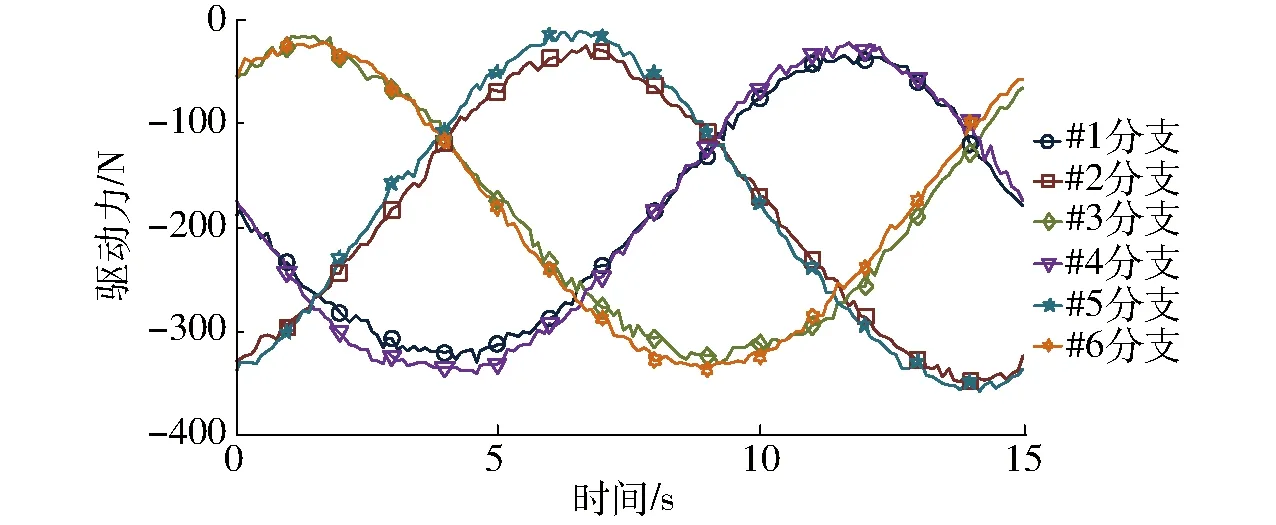
图13 驱动力同步协调控制下各分支实际驱动力Fig.13 Actual driving force distribution of driving force synchronous control

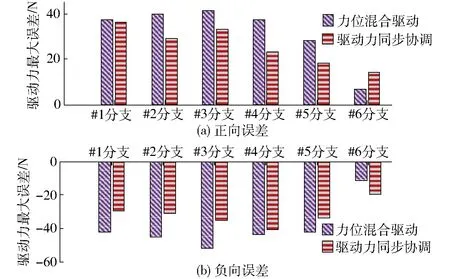
图14 各分支驱动力最大误差Fig.14 Maximum errors of driving force of each limb

由图6、12、13可得，较传统力位混合驱动模式而言，驱动力同步协调控制下的各分支实际驱动力波动较小，说明该方法下控制系统更加稳定。由图14和图15可得，较传统力位混合驱动方式而言，驱动力同步协调控制方式下的位置驱动关节驱动力误差有明显减小，而力驱动关节的驱动力误差有所增大，但各驱动分支间的驱动力误差较均匀，且整体变化范围小于传统力位混合驱动模式下的驱动力误差。说明力位混合同步协调控制方式可以有效提高各驱动分支间的驱动协调性。

5 结论

(1)在力位混合驱动模式的基础上，针对冗余驱动并联机构的驱动协调问题，提出了一种驱动力协调控制策略。

图15 各分支驱动力平均误差Fig.15 Average errors of driving force of each limb

(2)利用神经网络设计了驱动力同步控制算法，并基于机构动力学模型设计了神经网络自学习算法。

(3)分别采用传统力位混合驱动和神经网络同步控制两种方法对6PUS+UPU机构动力学仿真模型与样机进行了控制，对比结果显示，本文所提出的神经网络同步协调控制方法能够有效改善冗余驱动机构的驱动协调性。

1 FIRMANI F, PODHORODESKI R P. Force-unconstrained poses for a redundantly-actuated planar parallel manipulator [J]. Mechanism and Machine Theory, 2004, 39(5): 459-476.

2 DASGUPTA B, MRUTHYUNJAYA T S. Force redundancy in parallel manipulators: theoretical and practical issues [J]. Mechanism and Machine Theory, 1998, 33(6): 727-742.

3 O’BRIEN J F, WEN J T. Redundant actuation for improving kinematic manipulability[C]∥Proceedings of 1999 IEEE International Conference on Robotics and Automation, 1999: 1520-1525.

4 ZHAO Y J, GAO F. Dynamic performance comparison of the 8PSS redundant parallel manipulator and its non-redundant counterpart—the 6PSS parallel manipulator [J]. Mechanism and Machine Theory, 2009, 44(5): 991-1008.

5 陈修龙, 蒋德玉, 陈林林, 等. 冗余并联机构运动学性能分析与优化[J/OL]. 农业机械学报, 2016, 47(6): 340-347. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160645&flag=1. DOI：10.6041/j.issn.1000-1298.2016.06.045.

CHEN Xiulong, JIANG Deyu, CHEN Linlin, et al.Kinematics performance analysis and optimal design of redundant actuation parallel mechanism[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 340-347.(in Chinese)

6 LIANG Dong, SONG Yimin, SUN Tao, et al. Optimum design of a novel redundantly actuated parallel manipulator with multiple actuation modes for high kinematic and dynamic performance [J]. Nonlinear Dynamics, 2016, 83: 631-658.

7 ZHAO Y J, GAO F, LI W M, et al. Development of a 6-DOF parallel seismic simulator with novel redundant actuation [J]. Mechatronics, 2009, 19 (3): 422-427.

8 MULLER A, MAISSER P. Generation and application of prestress in redundantly full-actuated parallel manipulators [J]. Multibody System Dynanics, 2007, 18: 259-275

9 MULLER A. Consequences of geometric imperfections for control of redundantly actuated parallel manipulators [J]. IEEE Transactions on Robotics, 2010, 26(1): 21-31.

10 MULLER A. Internal preload control of redundantly actuated parallel manipulators-its application to backlash avoiding control [J]. IEEE Transactions on Robotics, 2005, 21(4): 668-677.

11 GANOVSKI L, FISETTE P, SAMIN J C. Piecewise overactuation of parallel mechanisms following singular trajectories: Modeling, simulation and control[J].Multibody System Dynamics, 2004, 12(4): 317-343.

12 CHAKRAOV D. Study of the antagonistic stiffness of parallel manipulators with actuation redundancy[J]. Mechanism and Machine Theory, 2004, 39(6): 583-601.

13 CHENG Hui, YIU Yiu-Kuen, LI Zexiang. Dynamics and control of redundantly actuated parallel manipulators [J]. IEEE/ASME Transactions on Mechatronics, 2003, 8(4): 483-491.

14 SHANG Weiwei, CONG Shuang, GE Yuan. Adaptive computed torque control for a parallel mamipulator with redundant actuation [J]. Robotica, 2012, 30:457-466.

15 SHANG Weiwei, CONG Shuang, GE Yuan. Coordination motion control in the task space for parallel manipulators with actuation redundancy [J]. Transactions on Automation Science and Engineering, 2013, 10(3): 665-673.

16 SHANG Weiwei, CONG Shuang. Robust nonlinear control of a planar 2-DOF parallel manipulator with redundant actuation [J]. Robotics and Computer-Integrated Manufacturing, 2014, 30: 597-604.

17 NIU Xuemei, GAO Guoqin, LIU Xinjun, et al. Decoupled sliding mode control for a novel 3-DOF parallel manipulator with actuation redundancy [J]. International Journal of Advanced Robotic Systems, 2015, 12:64-65.

18 NIU Xuemei, GAO Guoqin, LIU Xinjun, et al. Dynamics and control of a novel 3-DOF parallel manipulator with actuation redundancy [J]. International Journal of Automation and Computing, 2013,10(6): 552-562.

19 MULLER A, HUFNAGEL T. Model-based control of redundantly actuated parallel manipulators in redundant coordinates [J]. Robotics and Autonomous Systems, 2012,60: 563-571.

20 LAMAURY J, GOUTEFARDE M. Control of a large redundantly actuated cable-suspended parallel robot [C]∥2013 IEEE International Conference on Robotics and Automation (ICRA),2013: 6-10.

21 崔学良, 陈五一, 韩先国, 等. 基于Lagrange方程的3RPS/UPS冗余驱动并联机构柔顺控制[J]. 计算机集成制造系统, 2016, 22(10): 2434-2441.

CUI Xueliang, CHEN Wuyi, HAN Xian’guo,et al. Active compliant control strategy of 3RPS/UPS parallel machine with redundant actuating leg based on Lagrange equation[J]. Computer Inergrated Manufacturing Systems, 2016, 22(10): 2434-2441.(in Chinese)

22 WU Jun, WANG Jinsong, WANG Liping, et al. Dynamics and control of a planar 3-DOF manipulator with actuation redundancy [J]. Mechanism and Machine Theory, 2009, 44: 835-849.

23 WANG J S, WU J, WANG L P, et al. Homing strategy for a redundantly actuated parallel kinematic machine [J]. ASME Journal of Mechanical Design, 2008, 130(4): 044501-1-044501-5.

24 WU Jun, WANG Dong, WANG Liping. A control strategy of a two degrees-of-freedom heavy duty parallel manipulator [J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(6): 061007.

25 兰天, 刘伊威, 陈养彬，等. 机器人灵巧手基于关节交叉耦合同步控制[J]. 机器人, 2010, 32(2): 150-156.

LAN Tian, LIU Yiwei, CHEN Yangbin, et al. Synchronized cross-coupled control for base joint of dexterous robot hand [J]. Robot, 2010, 32(2): 150-156.(in Chinese)

26 段艳宾, 梁顺攀, 曾达幸, 等. 6-PUS/UPU并联机器人运动学及工作空间[J]. 机械设计,2011, 28(3): 36-40.

DUAN Yanbin, LIANG Shunpan, ZENG Daxing, et al. Kinematics and workspace analysis of 6-PUS/UPU parallel manipulator[J]. Journal of Machine Design, 2011, 28(3): 36-40.(in Chinese)

27 段艳宾, 梁顺攀, 李聪, 等. 6-PUS/UPU并联机器人冗余驱动力控制仿真[J]. 计算机集成制造系统. 2011,17(10):2195-2201.

DUAN Yanbin, LIANG Shunpan, LI Cong, et al. Simulation for redundant actuation force control of 6-PUS/UPU parallel manipulator[J]. Computer Integrated Manufacturing Systems, 2011,17(10):2195-2201.(in Chinese)

28 梁顺攀, 高思慧, 韩兴, 等. 6-PUS/UPU 并联机器人动力学建模及仿真[J]. 系统仿真学报, 2012, 24(9): 1839-1843.

LIANG Shunpan, GAO Sihui, HAN Xing,et al. Dynamics modeling and simulation of 6-PUS/UPU parallel manipulator[J]. Journal of System Simulation, 2012, 24(9): 1839-1843.(in Chinese)