气体搅拌下厌氧消化反应器CFD数值模拟及模型研究

王 乐 樊 敏 詹翔宇 杨顺生

(1.西南交通大学土木工程学院, 成都 610031; 2.西南科技大学环境与资源学院, 绵阳 621010)

0 引言

厌氧消化作为一种高效、高经济性、广泛性的生化处理方式,被用于化工环保领域处理禽畜废水和固体废弃物等[1-2]。其中，厌氧消化过程中反应器内的搅拌方式影响着厌氧消化过程的能源消耗以及最终的处理效果。反应器内的搅拌方式包括机械搅拌[3-5]和气体搅拌,气体搅拌采用沼气或空气通入反应器,利用气体与液体的动能交换,搅拌反应器内的液体[6-8]。

由于厌氧消化反应器内液相介质往往为非牛顿流体(如污泥或废水等),这些介质具有不透明特性,采用传统的粒子图像测速法(Particle image velocimetry, PIV)及激光多普勒测速(Laser Doppler velocimetry, LDV)等检测方式无法测定反应器内部液相速度[9]。故有学者采用流变性质相同、且同样为剪切变稀的羧甲基纤维素(Carboxymethyl cellulose, CMC)溶液替代反应器内非牛顿液相介质,其为透明液体能够采用PIV实验方法对反应器内速度场进行实验研究[10]。数值模拟技术的出现能够辅助反应器设计,便捷地获取反应器内流场、速度场等物理信息[11-12]。曹秀芹等[13]采用多重参考系法对构建的污泥厌氧消化反应器进行了数值分析,发现反应器底部、顶部以及壁面附近区域易形成死区。BRIDGEMAN[14]在对实验室规模的厌氧消化器研究中,发现采用计算流体力学(Computational fluid dynamics, CFD)技术能够观察到非牛顿液相下消化器内旋流流场,污泥浓度的增大明显影响到混合相速度。以上研究以机械搅拌为研究对象,对于气体搅拌,由于欧拉双流体模型通过植入非牛顿曳力系数及非牛顿剪切应力,能够表征液相的非牛顿特性及气液两相相间作用力,因此被应用于非牛顿气液两相的数值模拟[9-10]。WU[5,15-18]对厌氧消化池的不同搅拌方式进行了一系列研究,其中厌氧消化池的气体搅拌效应采用欧拉双流体模型进行数值模拟,并根据模拟结果给出反应器优化建议。DAPELO等[10]采用数值模拟方法对厌氧消化反应器内气体搅拌进行模拟研究,与实验结果比对后发现，流量为8.63 mL/s时欧拉-拉格朗日架构下模拟结果能够反映反应器内速度场及剪切速率。然而气液两相的模拟仍然存在着多相湍流问题，至今尚未从理论上得到合理解决,不同的相间作用力以及多相流模型的适用性在不同文献中仍有不同的观点,这些均需要与实验结果进一步验证后确定[19]。

本文采用CFD技术对气体搅拌作用下厌氧消化装置内不同流量下的非牛顿液相(CMC溶液)速度场、动力黏度以及流场进行模拟，探讨多相湍流模型、相间作用力以及两相模型的选取对反应器内液相速度场的影响，为气体搅拌作用下厌氧消化反应器设计过程中数值模拟模型的选用及反应器搅拌优化提供理论依据。

1 数学模型

质量守恒方程为

(1)

动量守恒方程为

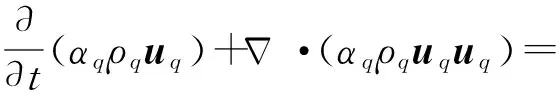
(2)

式中u——速度ρ——密度

α——体积分数

τ——剪切应力张量

p——压强g——重力加速度

F——相间作用力

下标q用于相区分,液相时q为l,气相时q为g。

反应器内液相为非牛顿液体CMC溶液,其剪切应力张量τ的表征采用Ostwald de Vaele模型进行描述，即

(3)

式中K——黏度系数n——流变特性指数

方程(2)中,相间作用力包括了升力(D)FD,曳力(L)Fl以及湍流扩散力(T)Ft,其表述为

F=FD+Fl+Ft

(4)

其中

(5)

(6)

(7)

式中Cl——升力系数,取0.5[20]

Ct——常数,取1[21]

σ——弥散普朗特数,取0.9[21]

KC——相间交换系数

Dl——湍流弥散量

CD——曳力系数d——气泡直径

曳力系数计算采用适用于非牛顿液相的公式通过自定义程序(User define function, UDF)程序实现,其公式为[22]

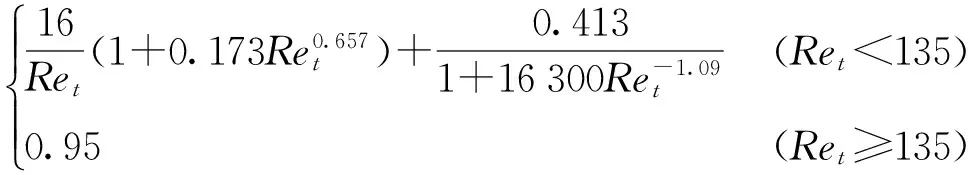
(8)

式中Ret——球形气泡雷诺数

多相湍流模型分别采用了标准k-ε模型,重整化群k-ε模型以及可实现k-ε模型以考察不同多相湍流模型对反应器内液相速度的预测能力。本文给出了适用于多相的标准k-ε模型(Standardk-ε),其表述为

(9)

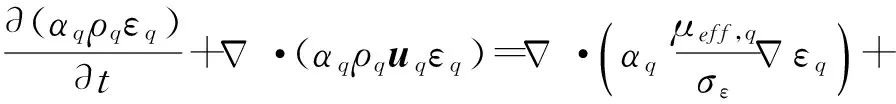
(10)

式中k——湍动能ε——湍动能耗散率

μeff,q——湍流粘性系数

C1、C2——常数

σk、σε——湍流普朗特数

Gk,q——湍动能产生项

Πkq、Πεq——气相对液相的影响项

重整化群k-ε模型(RNGk-ε)以及可实现k-ε模型(Realizablek-ε)参照文献[23]。此外,在两相流模型的研究中,将欧拉双流体模型耦合PBM模型以考虑反应器中气泡的聚并及破碎效应,具体的模型表述参照文献[9]。假设非牛顿与牛顿液相的聚并及破碎效应一致,忽略反应器内温度差异所带来的影响。

2 数值实现

2.1 物理模型

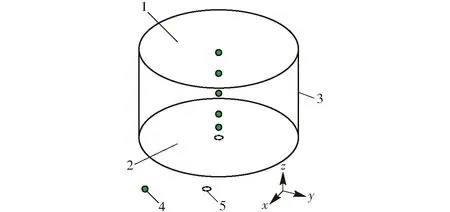
图1 厌氧消化器物理模型Fig.1 Physical model of anaerobic digester1.顶部 2.底面 3.壁面 4.气泡 5.入口

图1为计算的物理模型,与DAPELO等[10]的实验及数值模拟的厌氧消化反应器模型一致,其为总体积4 L的圆柱形反应器,底面圆的直径为20 cm,并从底面圆心通入直径为5 mm的管子作为气体入口,气体从此区域通入反应器并从顶部流出,在此过程中驱动液相流动达到搅拌的目的。

2.2 网格划分

采用如图2所示的非结构化网格进行计算。其中图2a为底面的网格划分,在圆中心区域网格数量较多,远离入口区域的网格尺寸较大,图2b为气体入口区域网格划分,采用四边形网格,图2c为x=0 m轴截面网格划分呈现中间较密、对称分布的特点,网格划分的总网格数量为108 720。

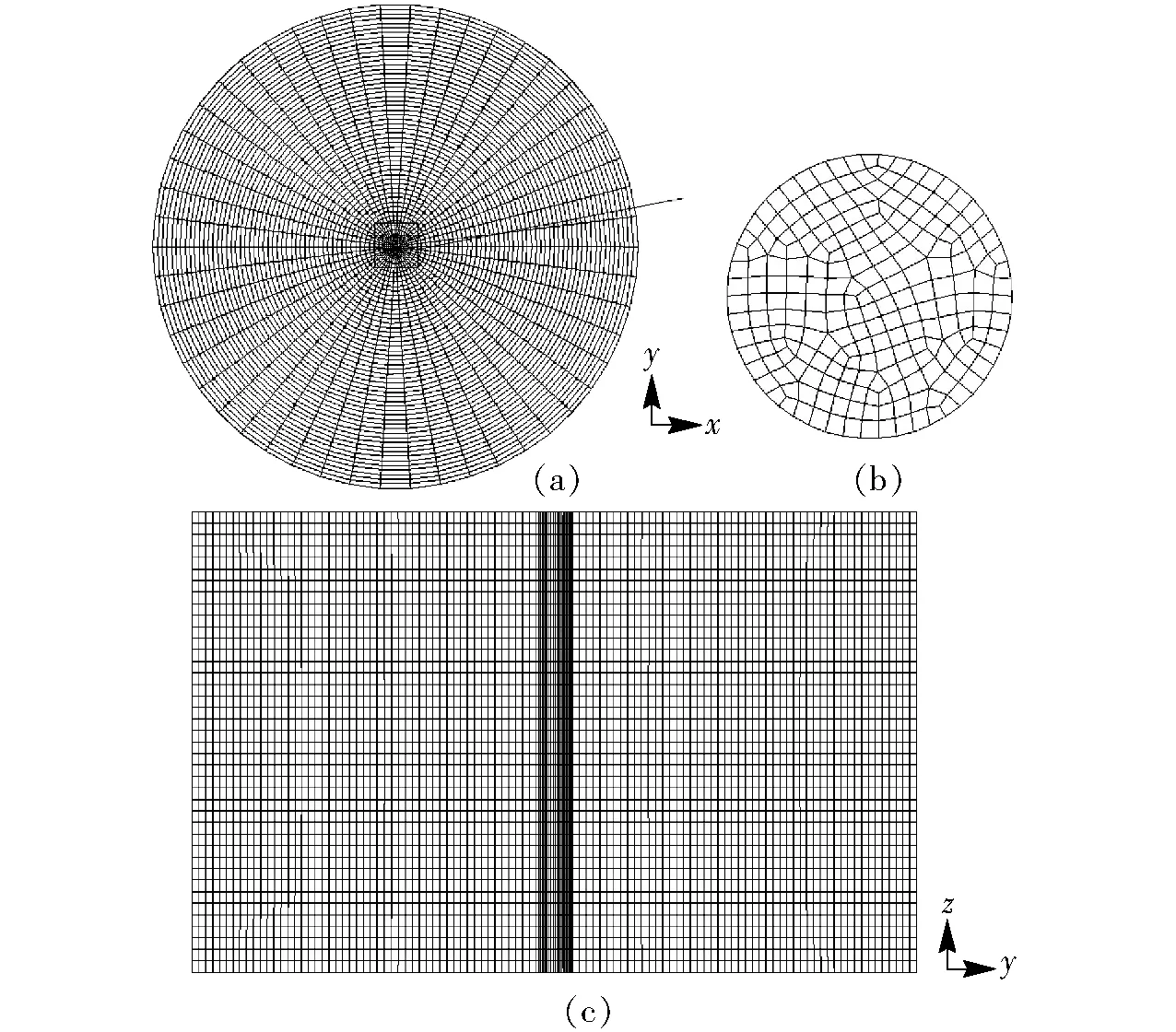
图2 网格划分Fig.2 Mesh generation

采用欧拉双流体模型计算气液两相流动时,计算域的网格数量增多模拟结果反而与实验吻合较差,其原因可能与湍动谱有关[24-25]。由于网格质量受网格大小、是否结构化网格、网格变化率等多种因素影响,以上因素的改变最终反映为网格数量的增减。因此,分别对网格数量为54 360、108 720、217 440、415 300的网格进行模拟并与实验结果进行验证后,选择模拟结果更加吻合实验结果的网格进行计算,该网格总数量为108 720。

2.3 计算方法及边界条件

采用Fluent软件[26]进行数值模拟计算,开启多相流模型中的欧拉双流体模块求解方程(1)～(8)、开启湍流模块求解湍流方程(9)、(10)以及隐藏模块求解群体平衡方程。采用有限体积法离散所有方程,体积分数项采用QUICK(Quadratic upwind interpolation for convective kinematics)格式进行差分,其它项采用二阶迎风格式,速度和压力耦合采用压力耦合方程组的半隐式算法(Semi-implicit method for pressure-linked equation, SIMPLE),残差设置为10-5。

入口采用速度入口边界条件,虽然实际工况中多采用沼气作为注入气体,但考虑到沼气的易燃、易爆特性及DAPELO等[10]在实验过程中采用的入口气体为空气,因此数值模拟采用空气注入,入口的流量参照实验分别为2.05、5.3、8.63 mL/s,出口为脱气入口边界条件,其他物理边界为固壁边界条件。

2.4 算例设置

除了对不同流量下反应器内流场、速度场以及动力黏度分布进行考察外,同时对相间作用力、两相模型、多相湍流模型的适用性一并进行探讨,表1为相关的算例设置。其中E-E代表欧拉双流体模型;E-E-PBM代表欧拉双流体模型耦合群体平衡模型;E-L代表欧拉-拉格朗日模型。

表1 不同算例设置Tab.1 Models for different calculation cases

3 结果与讨论

3.1 流线

图3为不同流量下反应器x=0 m轴截面流线。气体从底部注入反应器,在上浮过程中不断驱动液相运动,当气体上浮至反应器顶部时逸出,液相受到顶部边界条件的影响,向四周流动,到达反应器壁面后沿反应器壁向下流向反应器底部,最终形成两个对称的旋涡,从而起到反应器内液相搅拌的目的。图3中旋涡的中心位于反应器靠近中心区域的中上部,随着入口流量的增大反应器内旋涡结构及旋涡大小没有发生改变,这主要是由于入口流量较小,反应器物理模型规则,且气泡在非牛顿液相下为直线上浮所共同影响,这也与实验观察到的现象一致[10]。

图3 不同流量下x=0 m轴截面流线Fig.3 Streamline at axial cross section (x=0 m) with different flows

3.2 不同两相模型对液相速度影响

图4(图中U表示速度,r表示到反应器中心轴的距离,R表示反应器半径,H表示反应器高度)为不同入口流量、不同r/R位置处的液相速度,均呈现随着距离反应器中心越近,液相速度峰值越大,液相速度变化的幅度也越大。对比图4a、4d、4g,在贴近壁面区域(r/R=0.8),采用E-E-PBM、E-E以及E-L模拟得到的液相速度均能够反映实验值的大小和变化趋势；对比图4b、4e、4h,当处于反应器r/R=0.6位置时,不同多相流模型的模拟结果存在一定差异,但仍然能够呈现出反应器内液相速度的大小及变化。对比图4c、4f、4i,当接近反应器中心区域(r/R=0.4), E-L结果在入口流量为2.05 mL/s时预测能力较差,没有呈现出液相速度上升下降再上升的特点,而在8.63 mL/s时,如图4i所示,E-E、E-E-PBM模型模拟液相速度结果不及E-L模型。

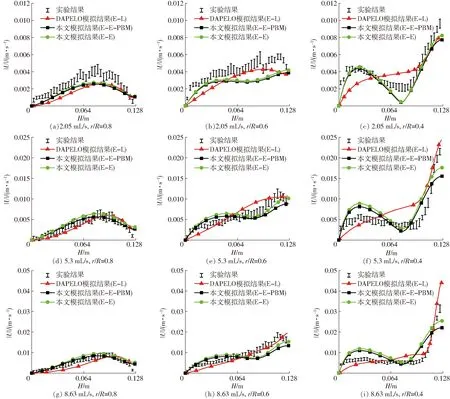
图4 不同流量、多相流模型、位置处的液相速度模拟值与实验值对比Fig.4 Comparison of simulated liquid velocity magnitude and experiment value at different flows, multiphase models and positions

观察图4,E-E模型与E-E-PBM模型之间差异较小,意味着耦合PBM模型并没有显著改善E-E模型的模拟结果,其可能原因是由于:低速下,气相流场相对稳定,较少地出现气泡聚并和破碎现象,在模拟过程中认为是单一粒径符合实际状况。但本文中E-E模型的气泡直径是采用实验得到的数据给定的,而E-E-PBM模型是通过给定初始气泡直径计算出反应器内的气泡粒径分布,这也意味着对于反应器内为不透明污泥或废水,无法准确测定反应器内气泡直径时,能够通过E-E-PBM模型得到较为理想的液相速度。

图5 不同流量下x=0 m轴截面液相动力黏度分布Fig.5 Dynamic viscosity distributions of liquid phase with different flows at axial cross section (x=0 m)

总之,在2.05、5.3 mL/s流量下,E-E以及E-E-PBM模型在不同r/R位置处模拟得到的液相速度显著优于E-L模型,而在8.63 mL/s下E-L模型模拟结果更为优异。与反应器壁面距离越近,不同模型的模拟结果越好。E-E模型及E-E-PBM模型对于反应器内液相速度的预测没有十分明显的差别。实际工况下厌氧消化反应器内含有固相物质(如污泥)时,由动量守恒定理可知,气相动量一部分转化为液相动量,一部分转化为固相动量,这将导致含有固相时反应器内液相速度低于不含固相时液相速度,但速度的变化趋势较为近似。

3.3 动力黏度分布

图5为反应器x=0 m轴截面的液相动力黏度分布,呈现着中间区域动力黏度较低,靠近壁面区域动力黏度较高,壁面角落位置动力黏度最高的特点,这也意味着反应器四周壁面及壁面角落位置的液相流动性较差不易被拌和均匀。其可能原因为非牛顿流体,液相在反应器器壁四周及角落位置由于受壁面条件及动能衰减的影响液相速度较低,剪切速率较大,导致反应器内这些区域的液相动力黏度较高。对比图5a～5c,随着入口流量的不断增大,反应器中心区域的动力黏度低值区域面积逐渐增大,反应器四周角落位置动力黏度的峰值逐渐减小。这意味着入口流量的增大能够有效改善反应器器壁四周及角落区域的流动性能。

3.4 相间作用力对液相速度影响

气液两相之间的作用力在多相流数值模拟中为重要影响因素,影响着计算结果的优劣,由于曳力在相间作用力中起着主要作用,其大小在气液两相流动中通常是其他作用力的数十倍以上[27],因此以曳力为基本的相间作用力,在流量为5.3 mL/s条件下,分别采用E-E及标准k-ε模型,考察升力以及湍流扩散力对液相速度模拟结果的影响。

如图6a所示,在距离反应器壁面较近的位置(r/R=0.8),不同的相间力所得到的模拟结果较为接近,与实验吻合良好。如图6b所示,在r/R=0.6位置,当只考虑曳力时,液相速度在反应器底部和中部预测准确,但在反应器上部低估了液相速度；考虑曳力、升力及湍流扩散力时,在反应器底部略微高估了液相速度；而考虑曳力及升力时模拟结果更为均衡地介于上述两者之间。如图6c所示,在r/R=0.4位置,不同作用力下均呈现底部区域液相速度模拟值过高,而上部区域液相速度模拟值过低的现象,其中相间作用力D+L组合对于顶部区域的预测更为准确,D+L+T组合次之,只考虑曳力时模拟结果最差。

图7 流量为5.3 mL/s时不同多相湍流模型下、不同位置处液相速度模拟值与实验值对比Fig.7 Comparison of simulated liquid velocity magnitude and experiment value for flow rate of 5.3 mL/s with different turbulence models at different positions

总之,相间作用力对于液相速度的影响主要体现在反应器r/R为0.6及0.4位置,采用D+L及D+L+T组合的液相速度模拟结果,高估了反应器下部区域液相速度,低估了上部区域液相速度,但总体上优于只考虑曳力的模拟结果。

3.5 多相湍流模型对液相速度影响

由于欧拉双流体模型中由湍流脉动引起的二阶项及高阶项需要湍流方程进行封闭[19],不同湍流方程模型对于多相流求解存在适用性问题。因此,采用欧拉两相模型并考虑相间作用力为升力和曳力,对不同多相湍流模型模拟得到的液相速度进行考察。如图7所示,采用标准k-ε和RNGk-ε湍流模型得到的液相速度模拟值与实验值吻合良好,并优于可实现k-ε模型。图7a中,在反应器贴近壁面位置(r/R=0.8),3种湍流模型均能反映液相速度的变化。而逐渐靠近反应器中心时,如图7b(r/R=0.6)和图7c(r/R=0.4)所示,距离反应器顶部较近的区域,可实现k-ε模型低估了此区域的液相速度值,较另外两种湍流模型预测的液相速度差异较大。其主要原因是由于每种湍流模型本身具有一定的局限性,模型的经验常数也存在一定的适用范围[28]。标准k-ε模型应用的广泛性强于其他2个模型,而RNGk-ε模型中ε方程引入了时均应变率,且不同的系数值由理论分析得出,故采用这两种湍流模型得到的液相速度模拟结果较为精确。由于反应器流场及旋涡结构简单,可实现k-ε模型主要针对时均应变率较大导致负应力的情形且适合模拟强璇流动,因此模型的优势及适用性并未充分体现,模拟结果较差。

4 结论

(1)随着气体流量的增加、厌氧消化反应器x=0 m轴截面的旋涡形态及分布未发生明显变化。反应器四周底部为动力黏度高值区,当气体流量增大时,液相动力黏度高值区面积及峰值分别减小。

(2)在入口流量为2.05、5.3 mL/s时,E-E以及E-E-PBM模型均可用于非牛顿液相下厌氧消化反应器内多相流的液相速度场的研究,且模拟效果优于E-L模型。在入口流量为8.63 mL/s时,E-L模型模拟效果优于E-E以及E-E-PBM模型。与反应器壁面距离越近,不同模型的模拟结果与实验结果吻合越好,未存在显著差异。E-E模型及E-E-PBM模型对于反应器内液相速度的预测没有显著差别。

(3)当入口流量为5.3 mL/s时,RNGk-ε及Standardk-ε湍流模型的液相速度计算结果与实验值吻合较好,优于可实现k-ε模型。相间作用力考虑为升力及曳力组合时,模拟得到的液相速度较为准确。

1 陈思思, 戴晓虎, 薛勇刚,等. 影响高含固厌氧消化性能的主要因素研究进展[J]. 化工进展, 2015, 34(3):831-839.

CHEN Sisi, DAI Xiaohu, XUE Yonggang, et al. Research progress of the main factors influencing properties of high-solid anaerobic digestion[J]. Chemical Industry and Engineering Progress, 2015, 34(3):831-839. (in Chinese)

2 盖希坤, 张良佺. 禽畜废水厌氧反应动力学研究[J/OL]. 农业机械学报, 2017, 48(1):245-251. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170132&flag=1. DOI:10.6041/j.issn.1000-1298.2017.01.032.

GAI Xikun, ZHANG Liangquan. Kinetic study on anaerobic reaction of livestock wastewater[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(1):245-251. (in Chinese)

3 曹秀芹, 赵振东, 杨平,等. 基于污泥流变特性对厌氧消化反应器的模拟研究[J]. 给水排水, 2016,42(7):36-41.

4 曹秀芹, 杜金海, 李彩斌,等. 污泥厌氧消化搅拌条件的优化分析[J]. 环境科学与技术, 2015, 38(1):100-105.

CAO Xiuqin, DU Jinhai, LI Caibin, et al.Optimal analysis on the mixing condition of sludge in the process of anaerobic digestion[J]. Environmental Science & Technology, 2015, 38(1):100-105. (in Chinese)

5 WU B. CFD simulation of gas mixing in anaerobic digesters[J]. Computers & Electronics in Agriculture, 2014, 109:278-286.

6 杜连柱, 陈羚, 张克强,等. 低强度空气搅拌对猪粪秸秆固体产酸发酵效果影响[J]. 环境工程学报, 2011, 5(1):209-213.

DU Lianzhu, CHEN Ling, ZHANG Keqiang, et al. Effect of low intensity air-stirring on solid acidogenic digestion with pig manure and straw as feedstock[J]. Chinese Journal of Environmental Engineering, 2011, 5(1):209-213. (in Chinese)

7 KARIM K, HOFFMANN R, THOMAS K K, et al. Anaerobic digestion of animal waste: effect of mode of mixing[J]. Water Research, 2005, 39(15):3597-3606.

8 KARIM K, HOFFMANN R, KLASSON T, et al. Anaerobic digestion of animal waste: waste strength versus impact of mixing[J]. Bioresource Technology, 2005, 96(16):1771-1781.

9 王乐,苏军伟,郑西朋,等.塔式曝气池内非牛顿活性污泥气液两相数值模拟[J]. 中国环境科学, 2017, 37(5):1783-1791.

WANG Le, SU Junwei, ZHENG Xipeng, et al. Numerical simulation of gas/liquid two-phase flow in the aeration tank with non-Newtonian activated sludge[J]. China Environmental Science, 2017, 37(5):1783-1791. (in Chinese)

10 DAPELO D, ALBERINI F, BRIDGEMAN J. Euler-Lagrange CFD modelling of unconfined gas mixing in anaerobic digestion[J]. Water Research, 2015, 85:497-511.

11 王宇, 王江云, 许双双,等. 高效厌氧生物反应器内的湍流特性及结构优化[J]. 石油学报(石油加工), 2016, 32(3):614-621.

WANG Yu, WANG Jiangyun, XU Shuangshuang, et al. Structure optimization and turbulent flow characteristics in high efficient anaerobic biological reactor[J]. Acta Petrolei Sincia (Petroleum Processing Section), 2016, 32(3):614-621. (in Chinese)

12 王雅君, 邱凌, 赵立欣,等. 热水循环加热厌氧反应器稳态数值模拟分析[J/OL]. 农业机械学报, 2016, 47(10):209-214. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161027&flag=1. DOI:10.6041/j.issn.1000-1298.2016.10.027.

WANG Yajun, QIU Ling, ZHAO Lixin, et al. Steady-state numerical analysis of anaerobic reactor by hot water circulating heating[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(10):209-214. (in Chinese)

13 曹秀芹, 赵振东, 杨平,等. 污泥厌氧消化反应器搅拌性能的CFD模拟[J]. 给水排水, 2016, 42(3):137-141.

14 BRIDGEMAN J. Computational fluid dynamics modelling of sewage sludge mixing in an anaerobic digester[J]. Advances in Engineering Software, 2012, 44(1):54-62.

15 WU B. CFD simulation of gas and non-Newtonian fluid two-phase flow in anaerobic digesters[J]. Water Research, 2010, 44(13):3861-3874.

16 WU B. CFD simulation of mixing in egg-shaped anaerobic digesters[J]. Water Research, 2010, 44(5):1507-1519.

17 WU B. Computational fluid dynamics investigation of turbulence models for non-Newtonian fluid flow in anaerobic digesters[J]. Environmental Science & Technology, 2010, 44(23):8989-8995.

18 WU B. CFD investigation of turbulence models for mechanical agitation of non-Newtonian fluids in anaerobic digesters[J]. Water Research, 2011, 45(5):2082-2094.

19 李希, 李兆奇, 管小平,等. 气液鼓泡塔流体力学研究进展[J]. 高校化学工程学报, 2015, 29(4):765-779.

LI Xi, LI Zhaoqi, GUAN Xiaoping, et al. Progress in hydrodynamics of gas-liquid bubble columns[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(4):765-779. (in Chinese)

20 ZHANG D, DEEN N G, KUIPERS J A M. Numerical simulation of the dynamic flow behavior in a bubble column: a study of closures for turbulence and interface forces[J]. Chemical Engineering Science, 2006, 61(23):7593-7608.

21 BUMS A D, FRANK T, HAMILL I, et al. The favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows[C]∥5th International Conference on Multiphase Flow, Paper No 392, 2004:1-17.

22 DEWSBURY K H, KARAMANEV D G, MARGARITIS A. Hydrodynamic characteristics of free rise of light solid particles and gas bubbles in non-Newtonian liquids[J]. Chemical Engineering Science, 1999, 54(21):4825-4830.

23 SHAH R E, SAJJADI B, RAMAN A A, et al. Solid-liquid mixing analysis in stirred vessels[J]. Reviews in Chemical Engineering, 2015, 31(2):119-147.

25 BUWA V V, RANADE V V. Dynamics of gas-liquid flow in a rectangular bubble column: experiments and single/multi-group CFD simulations[J]. Chemical Engineering Science, 2002, 57(22-23):4715-4736.

26 ANSYS Inc. ANSYS FLUENT-14.5 theory guide [M]. ANSYS Inc.,2012.

27 LABORDE-BOUTET C, LARACHI F, DROMARD N, et al. CFD simulation of bubble column flows: investigations on turbulence models in RANS approach[J]. Chemical Engineering Science, 2009, 64:4399-4413.

28 陶文铨. 数值传热学[M].2版.西安: 西安交通大学出版社, 2001.