基于分形噪声和几何着色器的经编毛绒织物仿真

张爱军， 蒋高明， 李欣欣， 丛洪莲(江南大学 教育部针织技术工程研究中心， 江苏 无锡 214122)

经编毛绒织物是经编织物中重要的一类产品。此类产品除具有经编线圈结构外，在表面还有毛绒覆盖。在经过定型、拉毛、梳毛等整理工序后，毛绒织物表面具有方向性的毛绒，这使得此类织物对光线的反射具有各向异性。而毛绒织物在使用过程中，毛绒受到外力作用其方向发生改变，从而会产生一定的随机性。由于这些特点，在进行渲染时，不能将毛绒织物表面简化为理想的镜面反射面进行计算。

目前对于毛绒织物仿真的研究有图像合成、二维绘制和三维绘制等方法。其中丛洪莲等[1]通过纹理合成的方法模拟毛绒，原始图像为真实织物，真实感强，但每种织物都需要预先采集对应的纹理，毛绒形态不能变化，前期需要建立合适的纹理库，工作量大。雷惠等[2]将图像像素化为粒子，再使用径向模糊算法实现毛绒效果的模拟，具体方法是通过在意匠图的所有像素点与其模糊中心点连线上取若干点像素值，将取得的所有像素值的平均值作为该点的新像素值。Xiong等[3]使用直线画法模拟毛绒效果，将毛绒纱描述为颜色渐变的线段。上述算法以二维图像或二维图形为处理对象，在仿真立体感上还需改善。更多的研究是使用三维模拟方法，包括几何方法和纹理方法。Csuri等[4]、Neulander[5]、Sadeghi等[6]使用几何方法绘制的毛绒较清晰，绘制效果好，但耗时较长，通常用于影视动画制作的离线渲染。Kajiya等[7]使用纹理方法绘制的毛绒绒感较强，效果柔和，但早期方法的速度尚不能满足针织产品计算机辅助设计过程中快速模拟的要求。Lengyel等[8-9]提出了一种基于层状纹理的毛绒绘制思想，在绘制效果和绘制速度方面得到了很好的兼顾，并成功应用在短毛动物模拟中。杨刚等[10]改进了Lengyel提出的算法，使其可以用于绘制玩具表面稍长的毛。唐勇等[11]改进了Lengyel提出的算法并应用在实时绘制毛发中。Wong等[12]、Lee等[13]分别用层状纹理实现了三维雪景和皮草时装的模拟。Zhang等[14]使用Lengyel方法生成了一种单针床提花毛绒的模拟。

通过观察可发现，经编毛绒织物表面毛绒的方向既具有整体上的确定性，又具有细节上的随机性，形成了自然的纹理。本文使用分形噪声来模拟毛绒的这一外观效果。此外，在经编织物计算机辅助设计系统中应用毛绒仿真时，考虑到对使用者的友好度，仿真效率和对计算机硬件资源的要求是必须要考虑的问题。而毛绒织物表面的毛绒数量大，生成毛绒的几何结构时需要消耗大量中央处理器(CPU)内存资源。为降低这一影响，本文在几何着色器中生成毛绒几何结构，从而减轻CPU的运算量，并减少CPU与图形处理器(GPU)之间传输的数据量。

1 毛绒方向的生成

1.1 分形噪声与毛绒方向的关系

现实中织物中毛绒方向并不完全一致，具有一定的随机性，在毛绒仿真时添加随机性可增加真实感。使用普通的随机数生成算法产生的噪声，其随机性在整个区域内分布平均，不具有纹理效果，表达结果不自然。本文使用分形噪声模拟毛绒方向的随机性。

分形噪声是对基噪声按不同频率采样，将采样结果进行叠加得到的混合噪声。本文使用的基噪声为二维噪声。生成基噪声的步骤如下。第1步生成随机数θ和随机数λ，如图1所示。假设毛绒的初始切线方向为三维坐标系中z轴方向，v为毛绒发生随机偏移后的方向，则θ表示偏移后的方向与初始方向的夹角。θ决定了毛绒偏移的大小，一般取小于45°的值，λ决定了毛绒偏移的方向，取值为0～360°。设毛绒的长度为1，用公式x=sinθcosλ，y=sinθsinλ，z=cosθ，可计算得到偏移后的位置坐标。根据三角函数的定义可知，x、y和z的值域为[-1,1]。用公式R=(x+1)/2×255、G=(y+1)/2×255、B=(z+1)/2×255 可将x、y、z转换到[0,255]值域中，用R、G、B表示RGB颜色空间中红、绿、蓝3个颜色通道，即得到基噪声图像F=f(R,G,B)。在毛绒织物仿真时，噪声图像F中1个像素的颜色值可反推得到1根毛绒的偏移向量，但此时图像F上的像素还是完全随机的，直接使用生成的毛绒方向杂乱，缺乏过渡，因而需要使用下面的方法生成分形噪声。

图1 随机数θ和λ示意图Fig.1 Schematic diagram of random θ and λ

1.2 多分辨率噪声的插值生成和混合

对基噪声按不同的采样系数采样可得到多幅长宽和基噪声图像相同的新噪声图像。设采样系数为k，则在基噪声图像上每k个像素点中取1个点作为采样点赋予新噪声图像。新图像上的非采样点的值可以通过对采样点平滑插值得到。本文选用的插值函数为柏林噪声[15]推荐的3t2-2t3。图2示出k=5时插值过程，对任意一个非采样点，找到与它相邻的4个采样点P(0,0),P(0,1),P(1,0),P(1,1)。对P(0,0),P(1,0)在x方向上插值得到P(x,0)，对P(0,1),P(1,1)在x方向上插值得到P(x,1)，再对P(x,0)和P(x,1)在y方向上插值得到P(x,y)。

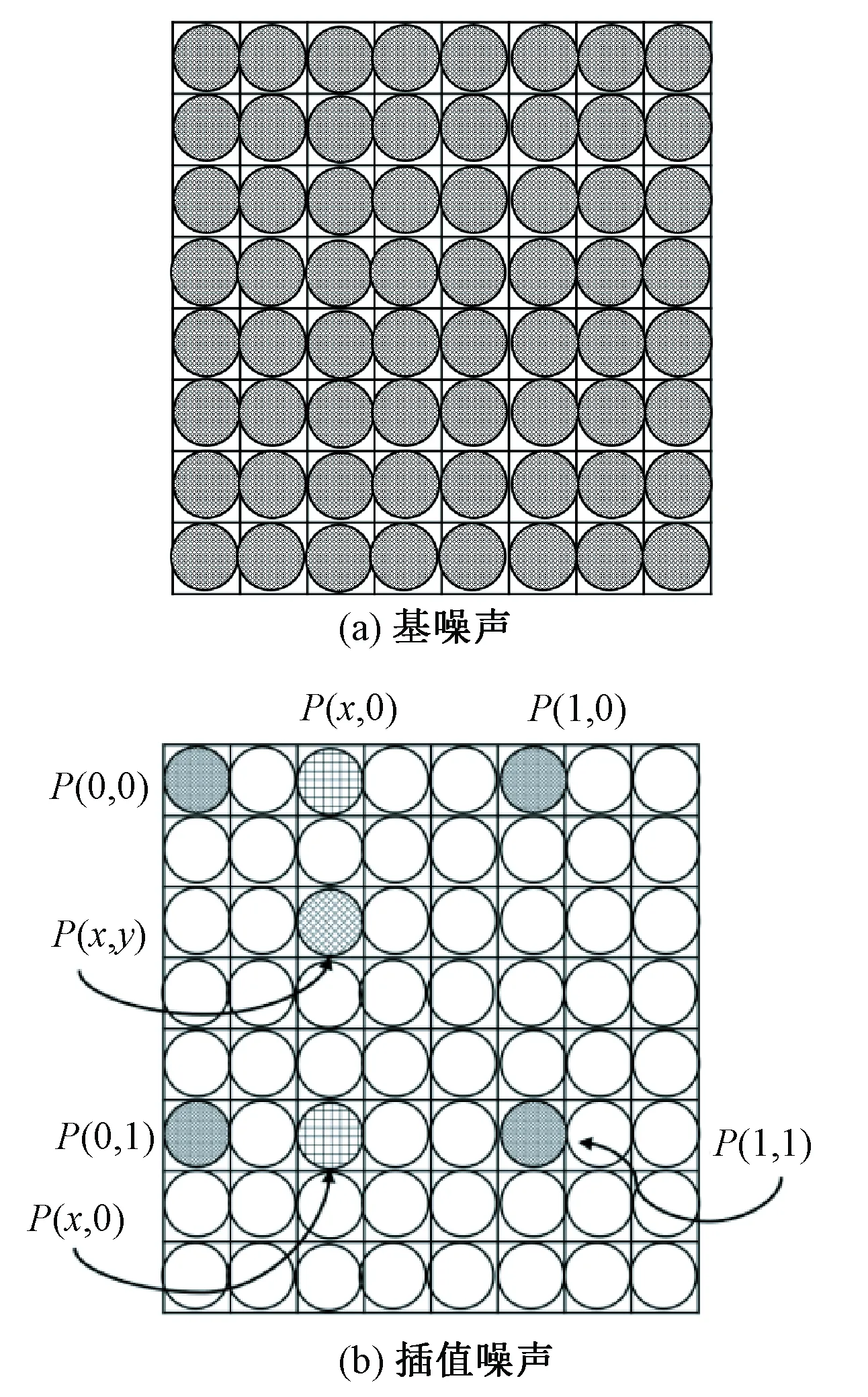
图2 噪声的插值方法Fig.2 Interpolation method of noise.(a) Basis noise; (b) Interpolated noise

对不同采样系数的噪声图像使用式(1)进行叠加混合即得到分形噪声图像。从公式可看出，采样系数越大的噪声所占比重越大，决定了分形噪声的基本形态。采样系数越小的噪声所占的比重越小，但是它为分形噪声提供了更多的细节信息。

(1)

式中：Pi为第i个采样频率的采样值；ki为其对应的采样系数；n为总的采样次数；P为最终合成的分形噪声。

图3(b)、(c)、(d)示出对基噪声图3(a)使用不同的采样率进行采样的结果。将图3(a)～(d)合成后得到的分形噪声如图3(e)所示。

图3 分形噪声的混合Fig.3 Mixing of fractal noise.(a)Basis noise; (b) Interpolated noise of k=2;(c) Interpolated noise of k=4;(d) Interpolated noise of k=8;(e)Fractal noise

2 毛绒几何结构的表示

2.1 毛绒的切片表示方法

本文假设绒纱为以圆为横截面，从根部到头部沿一定路径扫掠而成的半透明几何体。Lengyel等[9]通过将毛绒分为不同的层，使用纹理逐层渲染，绘制效果有较好的绒感，但该方法在视线与毛绒接近垂直时，层间会出现空隙，所以需要用毛翼纹理进行填充。本文同样是将一根毛绒分为不同的层进行渲染，不同的是本文使用了水平切片和垂直切片2种切片。无论是水平切片还是垂直切片，一层切片都是使用一个四边形表示，这使得切片很容易在几何着色器中通过一个点扩展生成。

图4示出水平每层切片都平行于织物表面和垂直每层切片都垂直于观察者视线方向切片。

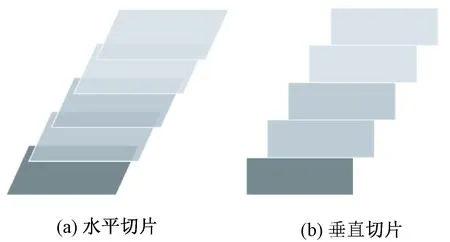
图4 水平切片和垂直切片Fig.4 Horizontal chip (a) and vertical chip (b)

2.2 切片类型的选择算法

在生成一帧织物仿真图时，通过算法判断当前视线下毛绒切片层间的空隙情况，选择不同的切片类型进行绘制。当视线与毛绒切线接近平行时，是以俯视的视角观察毛绒，不易产生空隙，使用水平切片渲染。当视线与毛绒接近垂直时，是以侧视的视角观察毛绒，容易产生空隙，则使用垂直切片。

图5为毛绒在视平面上的投影示意图。毛绒切片层间的空隙情况与层间距离l、毛绒半径r、视线与毛绒的夹角α等多个因素有关。层间的距离越大，毛绒的直径越小，视线与毛绒的夹角越大时，毛绒在屏幕上的投影越易出现空隙。

图5 毛绒在视平面上的投影关系Fig.5 Projection of plush on plane of vision

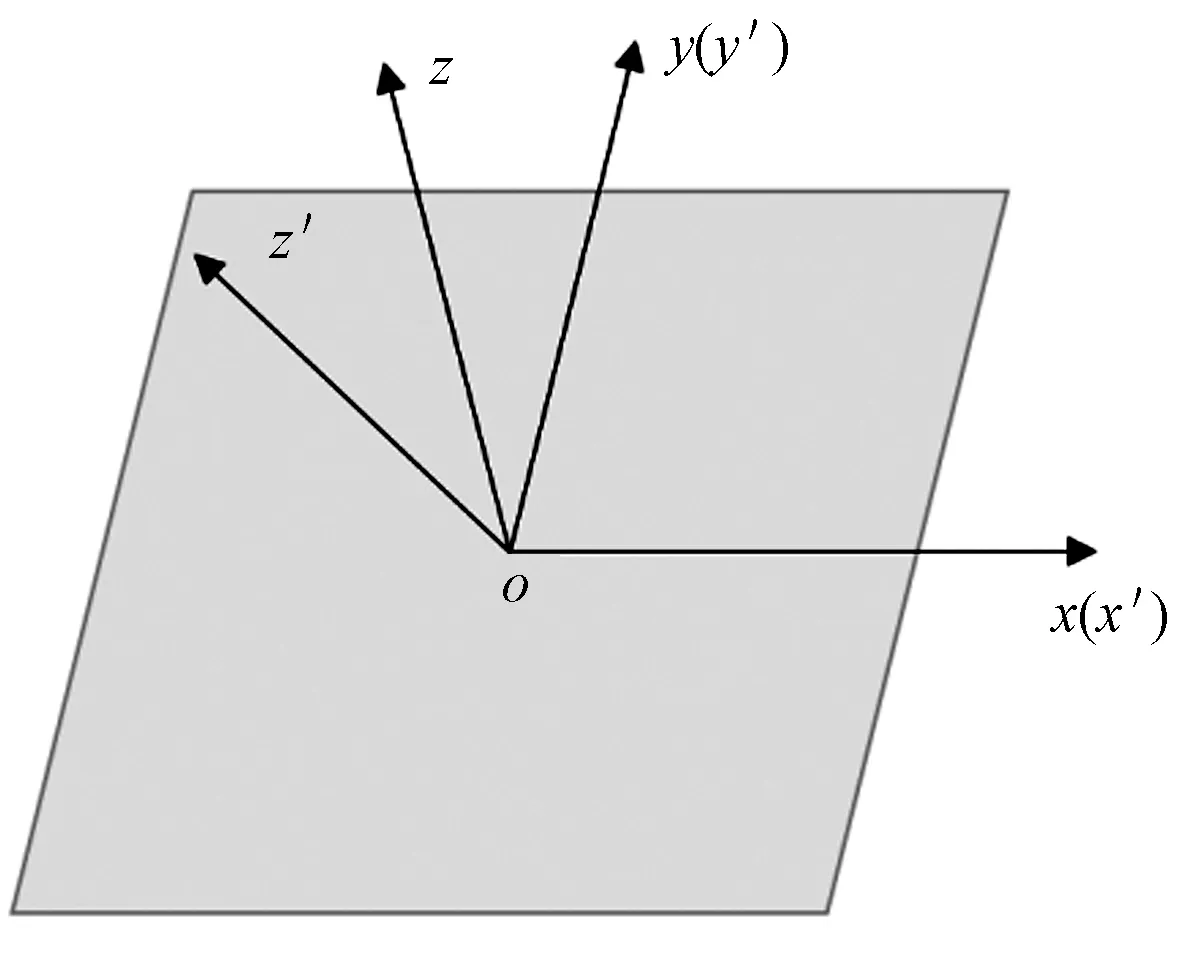
当2rcosα≥lsinα时，说明毛绒直径在视平面上的投影长度大于层间距离在视平面上的投影长度，此时使用水平切片。反之，当2rcosα

3 毛绒在几何着色器中的绘制

使用切片表示的毛绒，每根毛绒上有若干层切片，每个切片有一个四边形。一块织物上毛绒众多，如果由CPU完成所有毛绒结构的生成，数据量大且耗时较长。本文将这一过程迁移到几何着色器中执行。几何着色是现代可编程着色流水线的1个渲染阶段，它允许GPU根据需要改变输入的几何图元数据，输入的图元可以被拓展成1个或多个图元，也可以被删除。利用这一特性，可以将生成毛绒纱线几何结构的算法转移到几何着色器中，从而减少CPU向GPU传输的模型顶点数。本文中几何着色器中的输入为点图元，点图元的坐标值即是毛绒纱线根部中心点坐标。几何着色器的输出为三角形带，用于表示1个毛绒切片，即1段毛绒。每个三角形带包含2个三角形，由4个顶点定义。

毛绒段的4个顶点的坐标由输入的点图元、原始切线方向纹理、分形噪声纹理计算得到。计算步骤为：先将分形噪声纹理叠加到原始切线方向纹理得到毛绒实际方向，再根据实际方向与视线的关系选择使用水平切片或垂直切片的方法计算顶点坐标。

在生成分形噪声时，假设毛绒原始切线方向为z轴方向，而仿真时指定的毛绒方向不一定是z轴，因此，需要对噪声所包含的坐标进行坐标系转换。如图6所示，以1根毛绒的根部为原点，与织物横列平行且向右的方向为x轴正向，与织物纵行平行且向上的方向为y轴正向，与织物平面垂直的方向为z轴建立坐标系，该坐标系为父坐标系。将原点、x′轴、y′轴取为与父坐标系一致，以毛绒原始切线方向为z′轴，建立坐标系，该坐标系为子坐标系。设毛绒切线方向在父坐标系中用单位矢量(xt,yt,zt)表示，则分形噪声中的坐标(xs,ys,zs)可用式(2)从子坐标系转换到父坐标系，在父坐标系中的坐标表示为(xf,yf,zf)。

(2)

图6 父坐标系和子坐标系Fig.6 Parent coordinate system and child coordinate system

得到毛绒切线的实际方向后，按2.2节的方法选择切片类型。若需使用水平切片，则4个顶点的坐标可用式(3)计算得到图1(a)所示的切片；若需使用垂直切片，则4个顶点的坐标可用式(4)求得图2(b)所示的切片。

(3)

(4)

式中：P0、P1、P2、P3为四边形4个顶点的坐标；Pe为该段绒纱轴线终点坐标；Ps为该段绒纱轴线起点坐标；L为视线方向；R为毛绒切线方向与视线方向的叉乘；Wf为毛绒半径；Hf为毛绒段高度的一半。

在几何着色器中，除了计算得到毛绒几何结构的顶点坐标，还需要确定顶点的纹理坐标。本文假设的单根毛绒为圆柱形：水平切片是俯视毛绒时的效果，因此映射具有圆形图案的纹理而边缘透明的纹理；垂直切片为侧视毛绒时的效果，使用具有矩形图案的纹理。

由几何着色器生成的图元经过光栅化，在像素着色器中进行颜色混合输出最终的颜色，即可渲染出毛绒效果。

4 实验结果

本文算法基于DirectX 11实现。DirectX 是主流的图形渲染引擎接口，其渲染管线中的可编程阶段包括实现本文算法所需的顶点着色器、几何着色器和像素着色器。实验所用计算机CPU为Intel Core I7-6700, 内存为16 GB, 显卡为NVIDIA Quadro M1000。

图7示出织物实物图和仿真图。图7(a)为织物被手掌按压后的照片，按压后毛绒的方向发生了明显的改变，使织物反光发生改变，外观上形成了掌印。图7(b)是模拟这一效果的仿真图。仿真时除根据手掌按压位置改变了毛绒切线方向，还为毛绒方向叠加了分形噪声，因此在非按压位置也能看到不同区域有较平滑的外观变化。图7(c)为图7(b)中掌心位置的局部放大图。

图7 织物实物图和仿真图Fig.7 Fabric photos and simulation picture.(a) Fabric pressed by palm;(b) Simulation picture;(c) Enlarged partial

图7(b)中测试织物花高为384横列，花宽为240针，仿真耗时约750 ms。该耗时能满足计算机辅助设计软件快速仿真的要求。

5 结 论

本文用二维分形噪声表示经编毛绒织物中毛绒具有的随机感，多分辨率噪声的混合使某一处毛绒的随机性与周围毛绒有了一定的联系，形成了较为自然的效果。毛绒的实际几何切片由GPU根据分形噪声纹理在几何着色器中生成，减少了CPU和GPU之间数据的传输量，且能利用GPU的多核心运算能力提高算法的效率。算法在几何着色器中根据需要选用不同的切片类型，避免了单一平行切片会造成空隙的问题。

本文没有独立计算每根毛绒的阴影，因此，在表现毛绒之间的遮挡关系时有欠缺。此外,本文以单根毛绒为单位进行绘制，毛绒的柔和感弱于以一片区域为单位进行纹理绘制的方法。

FZXB

[1] 丛洪莲, 李秀丽. 基于纹理合成的提花绒类织物仿真[J]. 纺织学报, 2014, 35(10):150-155.

CONG Honglian, LI Xiuli. Simulation of jacquard pile fabric based on texture synthesis[J]. Journal of Textile Research, 2014, 35(10):150-155.

[2] 雷惠, 丛洪莲, 张爱军. 双针床短毛绒织物的CAD设计与仿真[J]. 纺织学报, 2013, 34(7):132-136.

LEI Hui, CONG Honglian, ZHANG Aijun. CAD design and simulation of double-needle bar short pile fabrics[J]. Journal of Textile Research, 2013, 34(7): 132-136.

[3] XIONG Y, MIU X H, JIANG A J, et al. Computer simulation for warp knitted brushed fabric with patterned pile[J]. Textile Research Journal, 2016,36(7):1659-1667.

[4] CSURI C, HAKATHORN R, PARENT R, et al. Towards an interactive high visual complexity animation system[C]//DEFANTI T, MCCORMICK B H, POLLACK B W, et al. Proceedings of the 6th Annual Conference on Computer Graphics and Interactive Techniques. New York: Association for Computing Machinery, 1979: 289-299.

[5] NEULANDER Ivan. Quick image-based lighting of hair[C]//BARZEL Ronen. ACM SIGGRAPH 2004 Sketches. New York: Association for Computing Machinery, 2004:43.

[6] SADEGHI I, PRITCHETT H, JENSEN H W, et al. An artist friendly hair shading system[J]. Acm Transactions on Graphics, 2010, 29(4):157-166.

[7] KAJIYA J T, KAY T L. Rendering fur with three dimensional textures[C]//THOMAS James J. Proceedings of the 16th Annual Conference on Computer Graphics and Interactive Techniques. New York: Association for Computing Machinery, 1989: 271-280.

[8] LENGYEL J E. Real-time Fur[C]//PEROCHE B, RUSHMEIER H. Rendering Techniques 2000. Vienna: Springer-Verlag GmbH, 2000: 243-256.

[9] LENGYEL J，PRAUN E，FINKELSTEIN A， et al． Real-time fur over arbitrary surfaces [C]//HUGHES J F, SEQUIN C H. Proceedings of the 2001 Symposium on Interactive 3D Graphics. New York: Association for Computing Machinery, 2001: 227-232.

[10] 杨刚, 曹卫群, 黄心渊. 基于层状纹理切片表示法的短毛造型系统[J]. 中国图象图形学报, 2008, 13(5):984-990.

YANG Gang, CAO Weiqun, HUANG Xinyuan. A fur modeling system based on multi-layer textured slices[J]. Journal of Image and Graphics, 2008, 13(5): 984-990.

[11] 唐勇, 邵绪强, 吕梦雅. 基于改进的 Lengyel 绘制方法的毛发实时模拟[C]//徐伯夏.第二届立体图象技术及其应用 (国际) 研讨会论文集.北京：中国图象图形学学会，2007:139-142.

TANG Yong, SHAO Xuqiang, LÜ Mengya. Improved Lengyel′s method based fur real-time simulation[C]//XU Boxia. Proceedings of the Second 3-D Image Technology and Application Conference. Beijing: China Society of Image and Graphics, 2007:139-142.

[12] WONG S, FU I. Hybrid-based snow simulation and snow rendering with shell textures[J]. Computer Animation & Virtual Worlds, 2015, 26(3/4):413-421.

[13] LEE J, KIM D K, KIM H S, et al. Real-time fur simulation and rendering[J]. Computer Animation & Virtual Worlds, 2010, 21(3/4):311-320.

[14] ZHANG A, LI X, XIONG Y,et al. 3D simulation model of warp-knitted patterned velvet fabric[J]. International Journal of Clothing Science and Technology, 2016, 28(6): 794-804.

[15] PERLIN K. Improving noise[J]. Acm Transactions on Graphics, 2002, 21(3):681-682.