前置掺气坎对弯道急流横向超高影响的数模研究

汪 厚 松， 刁 明 军， 蒋 雷， 王 军， 官 夏 菲， 任 昱

(四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065)

1 研究背景

在某些水利工程中，由于受地形和地质条件的限制，泄水建筑物不可避免地布置成弯道形式，而泄水建筑物中的水流通常是高速水流，水流属于急流状态，因此弯道急流是水利工程中常见的水流现象。许多专家和学者[1-3]发现了弯道水流现象并对弯道水流的机理进行了深入研究。王韦、许唯临[4]等对弯道水沙的运动进行了理论研究；王平义、蔡金德[5]等对弯曲河道的纵向垂线平均流速的平面分布进行了研究，推导出了变曲率动床弯道水流纵向垂线平均流速计算公式；刁明军、杨海波[6]等对弯道水流的研究现状进行了阐述，指出对弯道水流进行数值模拟研究将是一种趋势；杨玲霞、张银华[7]等通过水工模型试验对改善弯道急流流态进行了研究；惠爱瑙、王飞虎[8]等采用水工模型试验对大底坡急流弯道通气减蚀所形成的掺气空腔长度和水体掺气浓度进行了研究；吴宇峰、伍超[9]等通过模型试验对斜槛在急流弯道超高控制进行了研究，阐明了斜槛防治超高的原理，提出了斜槛的设计方法；许光祥、童思陈[10]等对单纯弯道下的水面横比降沿程分布进行了研究，得出了弯道横比降沿程分布特性及其统一计算公式。横向超高是弯道水流的一项重要指标，改善弯道水流横向超高具有重要的工程意义。在弯道前增设掺气坎对弯道急流横向超高的影响还缺乏研究，由于弯道的横向超高主要因弯道纵向流速沿横向分布不均匀所引起的，前置掺气坎的设置必将影响到弯道纵向流速沿横向分布，进而影响弯道横向超高。因此，有必要研究前置掺气坎对弯道急流横向超高的影响。

肖鸿、周赤[11]等采用数值模拟和模型试验对掺气减蚀设施进行了研究，将水深和流速的模拟结果与模型试验数据进行对比得出最大误差不超过2%，证明了Eulerian模型和VOF模型模拟掺气设施的可行性；罗永钦、刁明军[12]等采用模型试验和数值模拟对泄洪洞掺气减蚀设施进行了研究，水面线的模拟结果最大误差保持在3%以内，数值模拟表明k-ε模型和VOF方法能够准确地对泄洪洞掺气减蚀问题进行模拟与分析，特别是对自由水面捕捉和掺气空腔的长度模拟精度较高；叶茂、伍平[13]和漆力健[14]等采用数值模拟的方法对掺气坎后水流进行了研究，进一步证明了VOF方法在模拟自由水面和空腔长度的准确性。基于数值模拟方法研究掺气水流积累的成功经验，本研究以某工程的排洪隧洞的弯道为研究对象，采用标准k-ε模型与VOF模型对不同半径下的弯道在有无有前置掺气坎的情况下进行了数值模拟研究。

2 数学模型

本文采用的标准k-ε紊流模型，其方程组[15]如下：

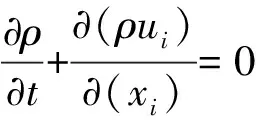
(1)

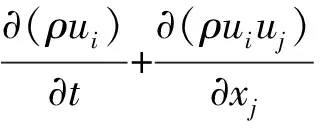
(2)

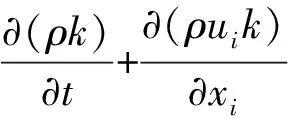
(3)

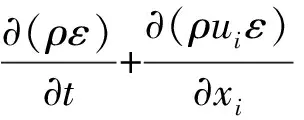
(4)

其中，ρ和μ分别为容积分数平均的密度和动力粘性系数,P考虑重力后的压强项，μt为紊动粘性系数，可以由紊动能k和紊动能耗散率ε按下式求出：

(5)

式中Cμ为经验常数;σk和σε分别为k和ε的紊流Prandtl数，C1ε和C2ε为ε方程常数。G为平均速度梯度引起的紊动能产生项，由下面的公式定义：

(6)

各常数取值见表1：

表1 紊流模型中常数的取值

采用VOF方法追踪水面。该方法认为计算域内水气交界面的网格空间由气相、水相混合充填，密度ρ和动力粘性系数μ为气相(水相)容积分数的函数：

ρ=αwρw+(1-αw)ρa

(7)

μ=αwμw+(1-αw)μa

(8)

式中αw为水的容积分数，ρw、ρa分别为水和空气的密度，μw、μa分别为水和空气的动力粘性系数。通过对水的容积分数αw的迭代求解，ρ和μ可以通过公式(7)、公式(8)求出。

本次模拟的区域从上游库区到弯道结尾直线段末端。溢流堰顶处桩号为(渠)0+000，掺气坎处桩号为(渠)0+320，弯道起始处桩号为(渠)0+370，明渠收缩段末端以下宽度均为5 m，如图1所示。掺气坎上游底坡为0.11，下游底坡为0.08，如图2所示。模型区域的整体网格数量为35万。由于弯道处为本次研究的重点，对弯道区域进行了加密处理，如图1所示。

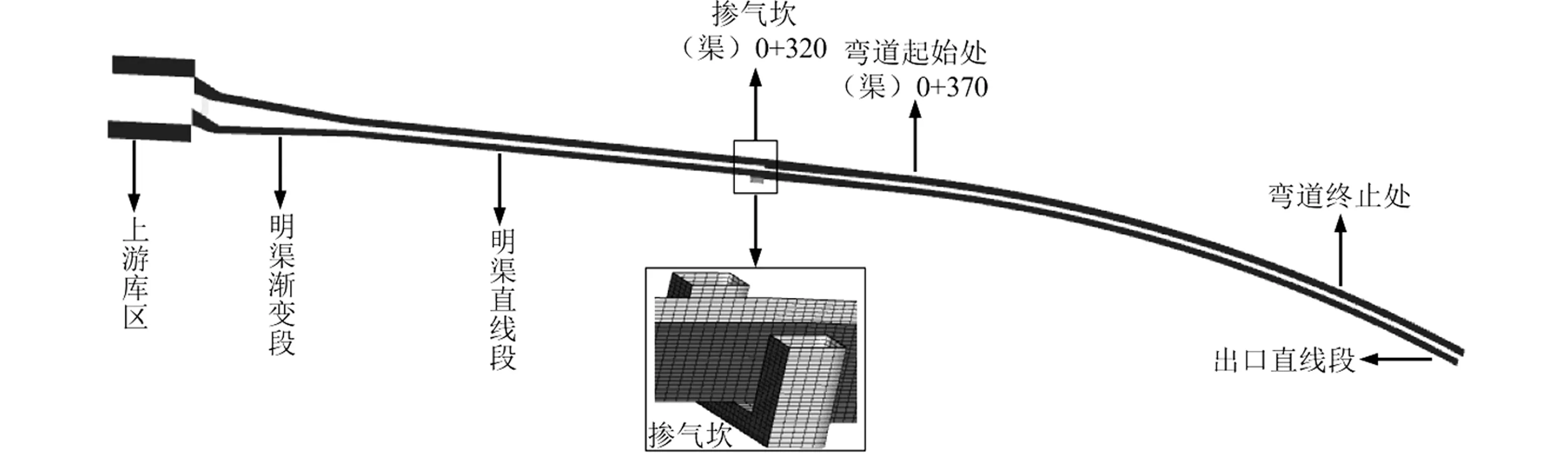
图1 计算域三维模型

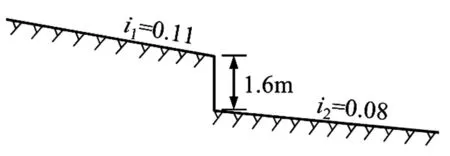
图2 掺气坎尺寸图

3 计算工况

本次数值模拟计算工况如表2所示：

4 结 果

由于数据提取和结果分析的需要，对于转弯半径为R=150 m，转弯角θ=47°的弯道，从弯道起始处开始，弯道全程等间距设置21个监测断面(编号为1到21)，各监测断面之间间距为6.15 m；对于转弯半径为R=500 m，转弯角θ=26°的弯道，从弯道起始处开始，弯道全程等间距设置37个监测断面(编号为1到37)，监测断面间距为6.33 m。由于弯道区域的流速较高，属于高速水流，弯道区域的流速均在20 m/s以上，存在强烈的掺气现象，故本文选取水气界面的体积分数为0.2的等值线作为自由水面，并对每个监测断面的左岸水深hl和右岸水深hr进行了提取，得到各工况下弯道段的横向超高Δh=hl-hr沿程分布，如图3所示。

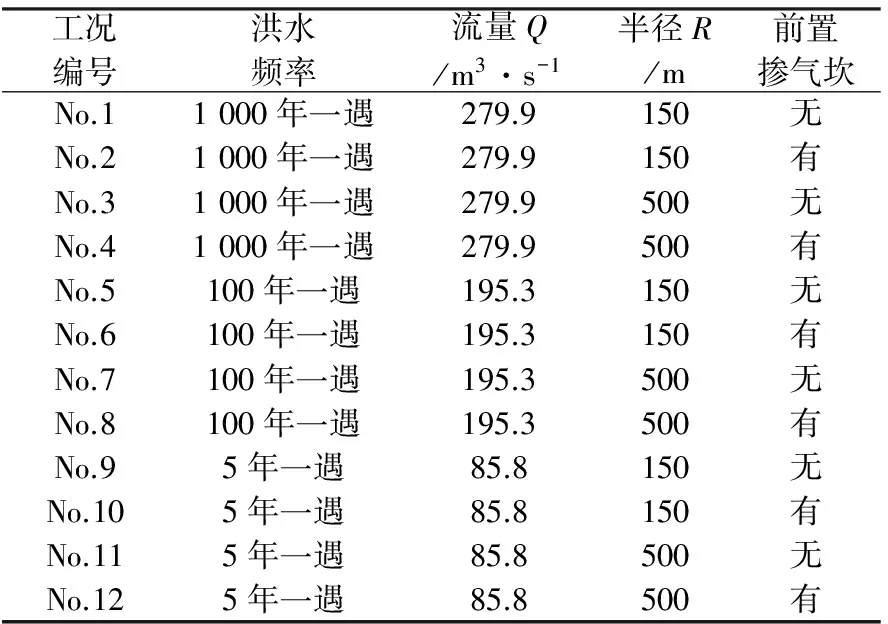
表2 计算工况

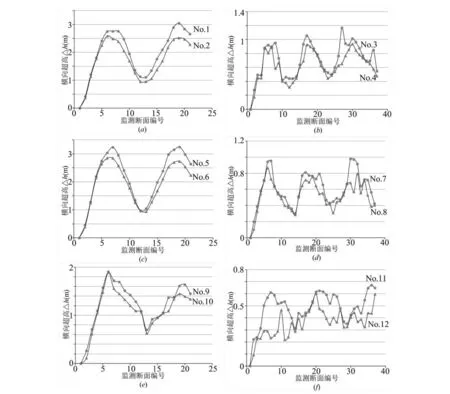
图3 横向超高沿程分布

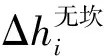
((9)

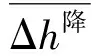
5 研 究

由图3可知，各弯道横向超高沿程呈波状分布，对于R=150 m的弯道，1～6号监测断面区域横向超高沿程逐渐增加，6～13号监测断面横向超高沿程超高逐渐减小，13～19号监测断面横向超高沿程逐渐增加，19～21号监测断面横向超高逐渐减小，波长特性约为73.8 m；对于R=500 m弯道而言，同样表现出类似于R=150 m时的沿程变化规律，相应的波长特性约为101.28 m。增设掺气坎和未设掺气坎的横向超高沿程波状分布同步，同一弯道不同流量下的波长特性相同，波幅特性随流量的减小而减小，波长特性主要受边壁条件控制。弯道内的急流由于弯道边壁偏转而产生扰动，所形成的冲击波经过弯道壁面反射向下游传播，导致横向超高沿程呈波状分布[16]。扰动因边壁的变化而产生，并经边壁反射向下游传播，因此，波长特性主要受边壁条件控制。增设掺气坎对弯道横向超高沿程波状分布规律基本无影响。

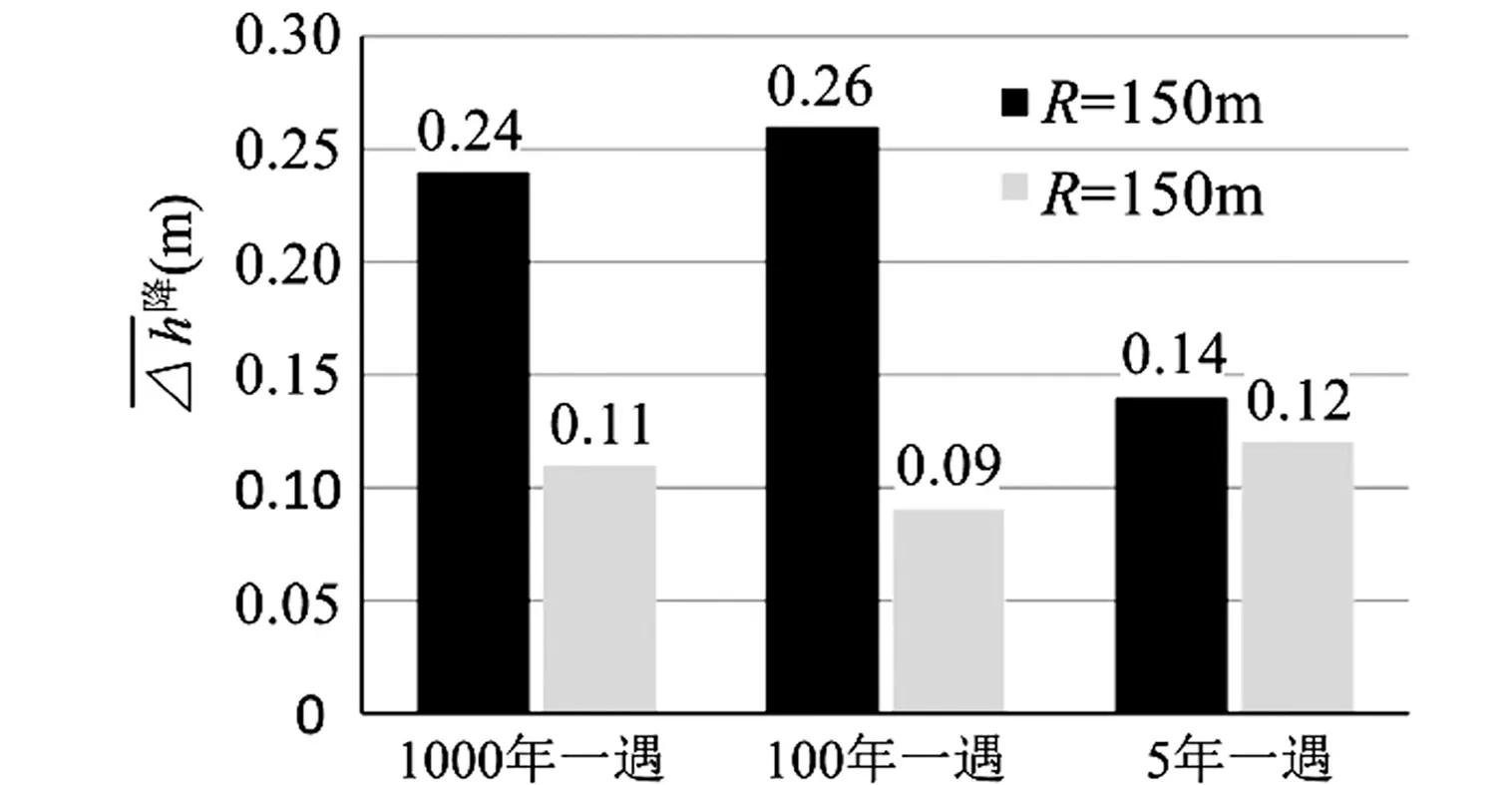
图4 各工况下横向超高平均降低值

在弯道前增设置掺气坎后，各个监测断面处的横向超高比未增设掺气坎时对应工况下的横向超高有所降低，横向超高降低值在横向超高沿程的第一个单调区间内表现不显著，基本为0，随后向下游逐渐表现显著，在R=150 m的弯道中横向超高最大降低值为0.507 m(1 000年一遇)、0.529 m(100年一遇)和0.275 m(5年一遇)，在R=500 m的弯道中横向超高最大降低值为0.436 m (1 000年一遇)、0.405 m (100年一遇)和0.376 (5年一遇)，如图3所示。弯道断面的水面形态取决于弯道纵向流速沿横向分布，由于水流经过掺气坎到跌落至底板的过程中，增加了水体与空气以及水体与水体之间的剪切摩擦，改变了水体原有的状态，使进入弯道的水体流场进行了重新分布，弯道纵向流速沿横向分布相对于未增设前置掺气坎时的流场发生了变化，强迫掺入的大量气体沿程外溢，使水流的紊动增强，改变了弯道区域原有流场，降低了流速分布的不均匀性，从而降低了弯道区域的横向超高。

由于监测断面取值存在离散性，因此本研究采用横向超高的平均降低值来反映前置掺气坎对弯道急流横向超高的整体改进程度。由图4可知，对R=150 m的弯道而言，掺气坎对弯道横向超高的整体改进程度在100年一遇工况时最大为0.26 m，在1 000年一遇工况时次之为0.24 m，在5年一遇工况时最小为0.14 m；对R=500 m的弯道而言，掺气坎对弯道横向超高的整体改进程度在5年一遇工况时最大为0.12 m，在1 000年一遇工况时次之为0.11 m，在100年一遇工况时最小为0.09 m。每种工况下，掺气坎对R=150 m的弯道的改进程度比对R=500 m的弯道改进的程度要大。在同一掺气坎作用下，弯道半径越小，弯道横向超高整体改进效果越显著；掺气坎对同一弯道的横向超高改进效果还受流量的影响。

6 结 论

本研究运用数值模拟的方法，对不同半径的弯道急流在有无前置掺气坎条件下的横向超高进行了研究，得出了以下结论:

(1)在弯道前增设掺气坎可降低弯道急流的横向超高，并且对弯道急流横向超高的沿程波状分布规律基本无影响，此措施可为类似的工程提供改善弯道急流横向超高的经验；

(2)前置掺气坎对弯道急流横向超高的整体改进程度与弯道半径有关，半径越小，改进程度越显著，掺气坎对同一弯道横向超高的改进程度还受流量的影响。

[1] 罗索夫斯基著，尹学良译.弯道水流的研究[J].泥沙研究，1958，3(1)：83-95.

[2] THOMSONJ.On the origin and winding of rivers in alluvialplains[M].Proc.Royal Society of London，1876，25(3):83-88.

[3] 刘焕芳.弯道自由水面形态的研究[J].水利学报，1990(4)：46-50.

[4] 王韦，许唯临，等.弯道水沙运动理论及应用[M].成都：成都科技大学出版社，1994(7)：27-50.

[5] 王平义，蔡金德，等.弯曲河道纵向垂线平均流速平面分布的研究[J].水动力学研究与进展，1994(6)：267-275.

[6] 刁明军，杨海波，等.弯道水力学研究现状与进展[J].西南民族大学学报(自然科学版)，2007，33(3)：597-599.

[7] 杨玲霞，张银华，等.改善弯道急流流态的实验研究[J].中国农村水利水电，2006(7)：77-79.

[8] 惠爱瑙，王飞虎，等.大底坡急流弯道通气减蚀水力特性研究[J].西北水资源与水工程，1997，8(2)：55-59.

[9] 吴宇峰，伍超，等.斜槛在急流弯道控制超高的设计研究[J].水力发电学报，2007，26(3)：78-81.

[10] 许光祥，童思陈，等.弯道水面横比降沿程分布特性研究[J].水力发电学报，2009，28(4):115-118.

[11] 肖鸿，周赤，等.掺气减蚀设施数值模拟研究探讨[J].长江科学院院报，2014，31(10)：115-119.

[12] 罗永钦，刁明军，等.高坝明流泄洪洞掺气减蚀三维数值模拟分析[J].水科学进展，2012，23(1)：111-115.

[13] 叶茂，伍平，等.泄洪洞掺气水流的数值模拟研究[J].水力发电学报，2014，33(4)：106-108.

[14] 漆力健，廖华胜，等.低弗劳德数掺气坎空腔回水问题研究[J].水利学报，2007，38(7)：819-825.

[15] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京：清华大学出版社，2004：120-123.

[16] 吴持恭.水力学：下册(第四版)[M].北京：高等教育出版社，2008：311-324.