以生为本，培养数学逻辑推理能力

☉南昌大学附属中学 陈一君

新课标强调，教师应当注重在教学过程中培养学生的思维能力.数学相较于其他学科有着烦琐严谨的特点，培养学生的逻辑思维能力对于提高他们的学习效率与数学素养来说，具有十分重要的意义.笔者认为，教师在开展课堂教学时，应当以生为本，结合学生的认知规律与特点，有意识地训练学生的数学逻辑推理能力，提高教学的有效性.

一、动手操作，思考过程

苏霍姆林斯基曾经说过：“儿童的智慧在他们的手指尖上.”著名教育学家陶行知先生也曾提出了“教学做合一”这一著名的教学理论，他强调教师应当引导学生在实践中获得知识，通过手脑联盟，实现创造教育的目的.由此可见，手与脑有着千丝万缕的联系，教师应当注重结合教学内容组织动手操作活动，通过引导学生思考探究问题的过程，培养其逻辑推理能力.

比如，笔者在对《古典概型》这一节的内容进行教学时，为了引导学生深入理解古典概型的概念及公式，笔者组织学生展开了动手操作活动.笔者首先让学生每3到5个人自由结为一组，并分给了每个小组一个骰子.随后笔者向学生提问：“大家掷一掷骰子，观察向上的点数，看看会出现几种结果呢？基本事件是什么呢？”学生通过动手实践，快速得出答案：“共有6种结果，即点数分别为1、2、3、4、5、6. 所对应的基本事件为A1=‘出现1点’、A2=‘出现2点’、A3=‘出现3点’、A4=‘出现4点’、A5=‘出现5点’、A6=‘出现6点’.”紧接着笔者提问：“记事件B为‘出现的点数小于3’，那么事件B发生的概率为多大？”学生通过分析与讨论发现，只有当点数为1和2时，事件B才会发生，因此事件B由基本事件A1、A2组成.由古典概型的定义可知，基本事件发生的可能性是相等的，因此学生认为事件B发生的概率为P（B）紧接着笔者讲到：“现在大家利用统计的手段，小组合作进行试验，根据试验所得到的统计数据对上述结果进行验证.”最后学生通过展开动手操作活动，利用统计的方法成功验证了上述计算结果的正确性.随后笔者对这一动手操作活动的结论进行了推广：“在古典概型中，若基本事件总数为n，事件A包含的基本事件数为m，那么事件A发生的概率有多大？”学生通过思考上述操作的过程，最终总结出结论为P（A）

在上述教学活动中，笔者通过引导学生进行骰子试验的操作活动，不仅成功活跃了课堂气氛，使学生全身心投入到教学活动中来，同时引导学生体验了从一般到特殊的数学思想，培养了他们的逻辑思维能力，高效地达成了教学目标.

二、反思失误，剥茧抽丝

学习错误是学生参与学习过程必然伴随的现象之一，当学生出现错误时，教师若仅仅注重纠正错误并告知其正确的方法，则难以触及问题的本质，学生下次可能还会犯同类型的错误，不利于学生创造性思维的发展.笔者认为，教师应当善于将学生有思考价值的错误作为教学资源，引导学生对错误进行反思，剥茧抽丝，明确错误的产生原因，促进他们在反思过程中提高思维的批判性.

比如，笔者在对《等比数列》这一节的内容进行教学时，发现学生在处理下述类型的问题时常常犯错误，于是笔者在课上引导学生对其进行了反思.例如，已知数列｛an｝的通项公式是，判断这一数列是否为等比数列.有些学生在证明这一问题时，首先分别求解了数列前几项的值：因为所以得到了该数列为等比数列结论.很显然这种做法是错误的，逻辑推理犯了由特殊代替一般的错误.笔者首先引导学生对这一错误做法进行了分析与讨论，找到错误的根本原因.学生们通过讨论发现，无论列举多少个这样比值为2的例子，都属于特例，并不能反映出等差数列的本质特点：从第2项起，每一项与它前一项的比都为2，因此不能证明该数列为等比数列.最后笔者进行了点拨：“大家也能明白，特殊规律并不等同于一般规律，大家在做这类证明问题时，切忌再犯这类由特殊代替一般的逻辑推理错误.”

在上述教学活动中，笔者通过关注学生逻辑思维失误的表现，有针对性地引导学生进行了反思与总结，有助于促进他们“吃一堑，长一智”，提高自身的逻辑推理能力.

三、数形结合，尝试转化

数形结合是一种非常重要并且常用的数学思想与方法，熟练地掌握并使用这一数学方法，有助于学生提高数学的表达能力，开展有效的逻辑思维活动.因此笔者认为，教师在教学时应当注重向学生渗透数形结合的思想，引导学生善于通过转化对相关问题进行推理等活动，深化数学思维.

比如，笔者在对《集合的基本运算》这一章内容进行教学时，引导学生进行了习题训练，使他们学会从形的角度出发，利用文氏图或数轴求解集合问题.例如，已知集合A=｛x∈R|x≤5｝，B=｛x∈R|x≥1｝，那么A∩B等于什么？对于这一问题，利用数形结合的方法可以快速准确地进行求解，学生首先在数轴上分别表示出集合A与集合B的范围，然后观察数轴上两段重合的范围为｛x∈R|1≤x≤5｝，即A∩B=｛x∈R|1≤x≤5｝.又如，A=｛x|-2≤x≤5｝，B=｛x|m+1≤x≤2m-1｝且B不是空集，若A∩B=∅，求m的取值范围.在求解时，可以首先将集合A的取值范围在数轴上表示出来，通过观察可知，若想令A∩B=∅，只需要令m+1＞5或者2m-1＜-2即可，最后求得m＞4.最后笔者向学生提问道：“大家通过求解集合问题，获得了哪些感想与收获呢？”紧接着学生对解题方法与技巧进行了归纳与总结，例如，有的学生回答道：“我发现在解决集合问题时，要善于利用数轴表示集合关系，通过图形使问题直观易懂，可以很大程度上提高解题的速度.”可以看出该学生切实体会到了数形结合思想的优点，达到了笔者所期望的效果.

在上述教学活动中，笔者通过引导学生利用数形结合的思想求解集合问题，提高了学生对具体问题进行转化与推理的能力，锻炼了他们的数学逻辑思维，取得了很好的教学效果.

四、严谨表达，锤炼语言

数学语言是正确进行推演论证的重要工具，用于表达思维的成果，锤炼学生的数学语言是培养学生逻辑思维能力的重要一环.因此笔者认为，教师在对学生进行逻辑思维的训练时，应当注重引导学生善于用数学语言严谨表达思维过程，锤炼数学语言.

比如，笔者在对《垂直关系》这一节内容进行教学时，引导学生通过动手操作探究了直线与平面垂直的判定定理.如图1所示，学生过△ABC的顶点A翻折纸片，想办法使折痕AD与平面垂直.在笔者的一步步引导下，学生通过动手操作与分析讨论探究出了直线与平面垂直的判定定理：如果一条直线与一个平面内的两条相交直线相垂直，那么该直线与平面垂直.紧接着笔者追问道：“大家能否用符号语言表示这一定理呢？”笔者留给学生充足的时间进行思考与讨论，最后学生得到了正确的答案：若a⊂α，b⊂α，l⊥a，l⊥b，a∩b=A，则l⊥α，成功用数学符号语言表述出了直线与平面垂直的推导过程.

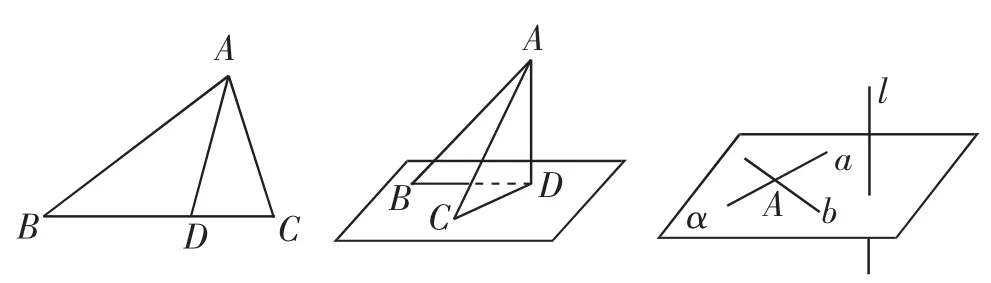
图1

在上述教学活动中，笔者通过有意识地训练学生的数学语言，促进学生在解题时能够用数学符号语言严谨地表述思维的过程，提高其解决问题的能力，深化逻辑思维，有效升华了学生的数学素养.

综上所述，教师在对数学展开课堂教学时，通过引导学生“动手操作”“反思失误”“数形结合”及“严谨表达”，能够在提高学生数学成绩的同时，有效发展学生的逻辑思维能力，贯彻新课标的教学要求，显著提高课堂教学的质量.F