辽宁省工业生态效率的空间分布与收敛性研究
关 伟,b,岂 宸
(辽宁师范大学 a.城市与环境学院;b.海洋经济与可持续发展中心,辽宁 大连116029)
1 引言
能源以及与能源消耗密切相关的气候变化、环境污染问题是当今人类社会面临的共同挑战,降低碳排放、提高能源利用效率是紧扣时代主题的全球性问题,我国一直是全球应对气候变化、环境污染事业的积极参与者。我国政府把绿色低碳发展作为生态文明建设的重要内容,将节能减排作为约束性指标纳入国民经济和可持续发展规划中。“十三五”时期是我国全面建设小康社会的决胜阶段,是推动能源革命的蓄力加速期。把能源消费总量和能源消费强度作为经济社会发展重要的约束性指标,建立指标分解落实机制,是政府落实能源发展目标的重要举措。能源作为工业的血液,工业活动中的能源消耗量在总能源消耗中占绝对比重。
从实践角度看,工业是国家能源政策的基本出发点,我国工业产值约占GDP的40%,而工业能源消耗量约占全国能源消耗总量的70%。工业生态效率研究是对工业能源效率问题的理论体系与实践应用领域的补充和完善,有关研究将为区域与工业能源发展规划与政策制定,为节能减排规划指标在各地区与工业各行业的量化分解,为工业相关产业的空间移动和结构优化提供理论支撑、量化依据和政策参考。

综上所述,我国大部分学者采用DEA测算模型对工业生态效率进行了测算,但是由于传统DEA数据包络分析得出的测算效率值是在确定前沿面之后得出的相对值,无法对所得数据进行时间序列分析,因此本文选择构建工业生态效率评价指标体系的方法来弥补这一缺点。借鉴何宜庆、陈林心、焦剑雄等构造的生态效率评价指标体系[6],建立工业生态效率评价指标体系,测度了辽宁省2000—2014年14座城市的工业总体生态效率并进行了研究,分析其收敛性与相关影响因素。
2 研究方法
2.1 工业生态效率评价指标体系
基于指标选择的科学性、可操作性和客观性等原则,借鉴已有的研究成果,充分考虑到辽宁省工业发展阶段、工业结构变动、区域经济发展规划、低碳经济发展战略和各地市资源禀赋差异的客观事实,借鉴何宜庆、陈林心、焦剑雄等人构建的城市生态效率评价指标体系[6],构建出辽宁省城市工业生态效率评价指标体系(表1),尽可能地充分反映出辽宁省工业生态效率的特有内涵和运行机制。其中,城市工业生态效率从生态环境效益、资源能源效益、经济效益和可循环经济4个维度11项指标进行考察,体现出工业生态效率是一个涵盖工业污染排放、工业能源消耗、工业经济发展和发展循环经济的综合系统,表征了工业发展对环境压力、生态环境现状和社会政策响应的“压力—状态—响应”环境测度体系的完整性。
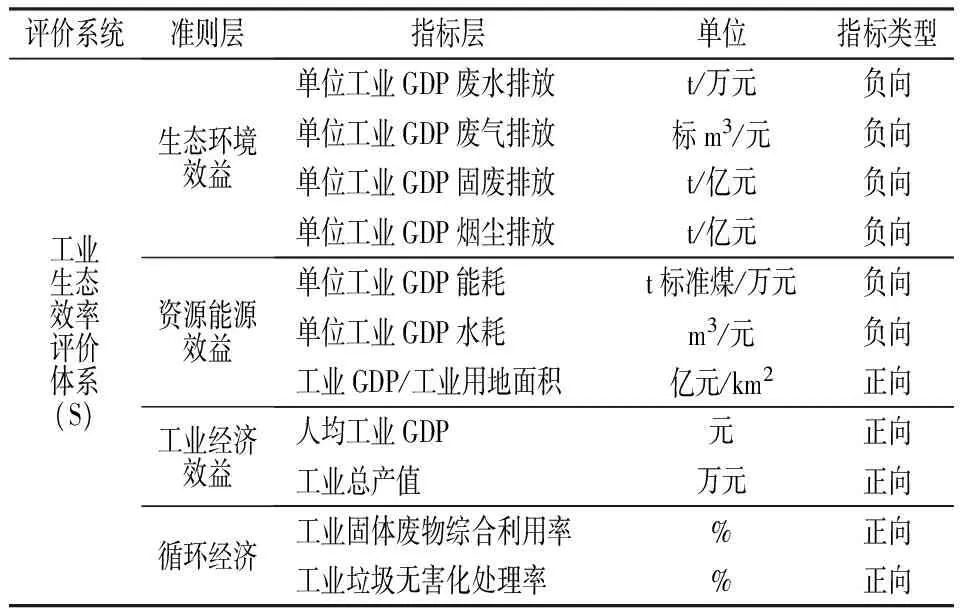
表1 辽宁省工业生态效率评价指标体系
在对辽宁省工业生态效率进行测度之前,我们首先要对各指标进行赋权。为了避免层次分析法、主成分分析法、专家打分法、因子分析法等方法的主观性对测度结果带来影响,引起非客观性和偏差性,本文运用熵值法来确定指标权重。
假设有m个样本、n项指标,根据原始数据可得原始矩阵xij=(xij)m×n。式中,xij代表第i个样本的j项指标值。
首先对原始数据进行标准化,文中采取的方式为min-max标准化。正向指标采用以下方式进行标准化处理:
(1)
负向指标采取以下方式进行标准化:

(2)
式中,max表示j项指标在有限个样本中的最大值;min表示j项指标在有限个样本中的最小值。
计算第i个样本第j项指标下指标值得比重:
(3)
计算各个指标的信息熵:
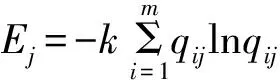
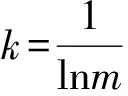
(4)
计算指标熵权值:
(5)
最终计算工业生态效率综合评价指数,计算公式为:
(6)
式中,Us表示工业生态效率综合系统S的评价指数;λsj表示第j项指标的权重;usj表示S系统的指标值。
2.2 工业生态效率收敛性模型
收敛性主要包括绝对收敛和条件收敛。绝对收敛是指各个决策单元随着时间的推移都会向同一稳态水平进行收敛运动,且具有稳定的增长速度。现实中,由于各个决策单元的特征和条件具有差异性,导致不同决策单元都有不同的稳态水平,并不断向各自的稳态水平趋同。如果各个区域间的工业生态效率呈现出收敛特性,那么表明已实施的提升工业能效、节能减排政策有利于缩小省内不同区域工业生态效率的差异性,可积极推进省内工业生态能源的均衡性;若是没有表征出收敛特性,说明省内工业能源效率未能向稳态水平趋近,需要对现有政策进行修改并加以完善。
σ收敛:σ收敛值是反映决策单元偏离被评价群体平均值的描述量,工业生态效率σ收敛则是表现各区域效率水平偏离总体水平,进而趋向不均衡的一个动态过程;若不同区域σ的值在时间维度上呈现出递减的趋势,则认定存在σ收敛。
本文对辽宁省工业生态效率的σ收敛分析的方程为:
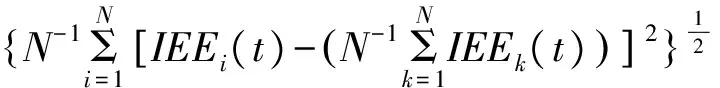
(7)
式中,IEEi(t)表示第i个地区在t时间段内的工业生态效率;N为区域个数。当σt>σt-1时,说明各个地区工业生态学率的离散系数在缩小,存在σ收敛;反之,则是发散的。
β收敛:β收敛又分为绝对β收敛和条件β收敛。如果不同区域之间的基期经济基础条件存在同一性,如地理环境、工业结构等,那么随着时间的推移,这些地区势必最终会趋于相同的稳态水平,实现绝对收敛,即盔对β收敛。
β收敛的验证方法主要有横截面分析方法和面板数据分析方法两种,文中使用的绝对β收敛回归方程为:
[ln(IEEi,T)-ln(IEEi,0)]/T=α+βln(IEEi,0)+ε
(8)
式中,IEEi,T、IEEi,0分别表示基期和T时间段内第i个地区的年均工业生态效率指数;[ln(IEEi,T)-ln(IEEi,0]/T表示第i个地区从基期到T时间段内的年均IEE增长率;α表示常量值;β表示基期工业生态效率(IEEi,0)项的系数;ε表示残差项。若式中β系数为正值,那么意味着各个区域的IEE增长率和各个区域的基期水平呈现出正向关系,工业生态效率在各个区域间的不均衡性有加剧的趋势,不存在β绝对收敛;反之,若β系数为负值,则各个区域的IEE增长率与初始水平具有负向关关系,存在工业生态效率低效地区“追赶”高效地区,趋近于同一稳态水平,存在β绝对收敛。与绝对β收敛不同,条件β收敛考虑了外生变量的作用,因此各个单元应该有不同的工业能源生态效率稳态。条件β收敛关注的是外生变量既定情况下,工业生态效率增长率与其效率稳态距离的反比关系是否仍成立,回归方程为:
[ln(IEEi,T)-ln(IEEi,0)]/T=α+βln(IEEi,0)+ΨXi,0+ε
(9)
式中,IEEi,T、IEEi,0分别表示基期和T时间段内第i个地区的年均工业生态效率指数;[ln(IEEi,T)-ln(IEEi,0]/T表示第i个地区从基期到T时间段内的年均IEE增长率;α表示常量值;β表示基期工业生态效率(IEEi,0)项的系数;ε表示残差项,Xi,0表示外生变量。
3 实证分析
3.1 研究区选择、变量选取和数据来源
本文选取辽宁省作为研究区域,根据数据的可得性,研究的时间跨度为2000—2014年。在测度工业生态效率值的时候,本文首先构建了工业生态效率评价指标体系(表1)。文中指标数据主要来源于2000—2014年的《辽宁统计年鉴》、《中国工业统计年鉴》、《中国环境统计年鉴》,部分缺失的数据由辽宁省各市政府工作报告、相关政府机构网站的数据补充,经统计整理合成2000—2014年辽宁省14个地市的数据集。
3.2 辽宁省工业生态效率测度与分析
运用工业生态效率评价指标体系测度辽宁省工业生态效率,得到辽宁省14个地级市2000—2014年的工业生态效率值(表2)。由表2可见,大连的工业生态效率最高,其次是沈阳和鞍山,平均值分别为0.997、0.982、0.945;而阜新市的工业生态效率为全省最低,生态效率平均值为0.655,仅为大连、沈阳和鞍山的65.5%、66.2%、69.3%。根据工业生态效率标准差可知,辽阳市的工业能源生态效率变动最剧烈,达到了0.150的全省最高值,其次为本溪和营口,工业生态效率标准差分别为0.138、0.138;大连市的工业生态效率标准差最低,波动程度最小。刘晓萌等认为,重点发展第三产业诸如旅游、服务等一些低污染的产业有利于城市转型与工业生态效率优化,且会缓和工业生态效率波动幅度[3]。大连市作为典型的沿海旅游城市与区域性服务业中心城市,大连市的高工业生态效率值和鲜有波动的变化情况与刘晓萌等的研究一致。

表2 2000—2014年辽宁省14个地级市工业生态效率统计值
为了进一步分析,本文将辽宁省14个地级市的工业生态效率值根据大小进行了排列分组:①低工业生态效率城市(0.60—0.75),此类型的城市个数在2000年、2007年、2014年的节点分别为4、4、3,所占比例分别为28.57%、28.57%、21.43%。②中等工业生态效率城市(0.75—0.90),此类型的城市在3个时间节点的个数分别为8、6、7,所占比例分别为57.14%、42.86%、50%。③高工业生态效率城市(0.90—1.10),此类型城市在3个时间节点的数量分别为2、4、4;其中所占比例为14.29%、28.57%、28.57%。以上数据清晰地反映了两个结论:一是在所有时间节点上,辽宁省的工业生态效率总体上处于高水平,类型以中度工业生态效率为主;二是从时间序列看,辽宁省的城市工业生态效率2000—2014年得到了显著提升,到2014年中高工业生态效率城市占全省的3/4以上。
运用ArcGIS软件对2000年、2007年、2014年3个时间节点的14个地级市的工业生态效率值进行空间可视化处理,得到图1。从图1可见,辽宁省的工业生态效率明显呈现出“中心—外围”分布趋势。在这4个时间节点上,沈阳市、大连市自始至终都是高工业生态效率值城市,周边城市按照距离沈阳市、大连市的远近呈现出特定变化:距离两座城市越近,效率值越高;距离越远,效率值普遍偏低。此外,从时间序列来考量,工业生态效率值的空间格局变化基本呈现出由“中心”不断向“外围”扩散的趋势,即以沈阳、大连两座高工业生态效率值型城市为“中心”逐步进行蔓延,直至全省格局变为以中高效率值城市为主。这表明在城市发展的过程中,除了受限于自身的资源禀赋、技术水平和基础条件之外,中心城市的辐射以及其带动作用也起到了关键性的作用。因此,在未来城市提高工业生态效率的发展道路上首先要重视并充分利用沈阳市、大连市的“中心带动”作用,以期向“外围扩散”提升整体工业生态效率水平。
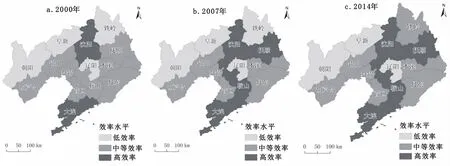
图1 辽宁省工业生态效率空间分布格局
3.3 辽宁省工业生态效率收敛性分析
省区作为我国区域工业经济管理的一级地域单元,全国范围内的工业发展、能源改革政策都必须通过省一级政府具体实施。因此,研究省内的工业能源生态效率的地区差异有助于全国尺度的工业发展政策在各省内的有效实施,有助于省内经济社会的和谐发展。
辽宁省作为东北老工业基地的龙头省份,尽管经过改革开放30年的发展取得了一定的成绩,但区域发展不平衡的问题仍然显著,尤其是工业生态效率方面的地区差异明显。为了更加系统地阐明辽宁省的区域差异,研究中我们将辽宁省分为辽东、辽中南、辽西北三大地区:辽东包括抚顺、本溪和丹东;辽中南包括有沈阳、大连、鞍山、营口、辽阳和盘锦;辽西北包括锦州、阜新、铁岭、朝阳、葫芦岛。准确描述和衡量辽宁省内工业生态效率的区域差距,探讨是否存在σ收敛、β收敛是本文必须要解决的两个问题。
σ收敛是指不同的地区之间工业生态效率的离差随着时间的推移而下降。通过式(7)计算每年的工业生态效率值的对数标准差,辽宁省总体工业生态效率对数标准差在2000—2014年间呈现出渐进式下降的趋势,从2000年的σ=0.009527下降到了2014年的0.006124,即辽宁省总体上存在σ收敛。对3个区域的研究发现,辽中南地区2000—2014年整体表现为σ收敛态势,工业生态效率的对数标准差由2000年的0.00623缩小到2014年的0.005854,总体上呈现出缓步下降趋势;辽西北地区的工业生态效率值尽管在2000—2014年间呈现出上下波动,但总体上表现出σ发散趋势,工业生态效率的对数标准差由2000年的0.001956缓增加到2014年的0.00256;而辽东地区在2000—2014年的工业生态效率对数标准差变化则呈现出“U”型。其中2000—2008年呈现出σ发散趋势,2009—2014年呈现出σ收敛趋势,总体上工业生态效率值的对数标准差是减小的。
绝对β收敛是指随着时间的推移,一个区域内所有地区的工业能源生态效率具有相同的趋势,利用式(8)作为收敛回归方程。在通过显著性检验的情况下,结果表明辽宁省各市的工业能源生态效率差异总体上在逐渐缩小,但收敛速度较为缓慢,为0.0538。辽中南地区以及辽东地区的工业生态效率通过绝对β收敛,趋同速度均高于全省平均水平,分别达到0.302、0.1925;而辽西北地区的β系数显著大于0,说明2000—2014年随着时间的发展,辽西北5市之间的工业能源生态效率逐渐拉开了距离,呈现出发散趋势。
条件β收敛表示各个单元向着自己的效率稳态趋同,彼此稳态之间不同,尽管长期发展,但工业生态效率水平高低的相对性依然存在。在绝对β收敛中,影响工业生态效率收敛情况的变量仅为工业能源生态效率的初始水平,但实际上取决于产业结构、技术创新等其他因素,将这些影响因素加入绝对β收敛模型之中,即为条件β收敛模型,则收敛方程为式(9)。
基于科学性、可操作性和客观性等原则,本文选取产业结构、对外开放程度、科技创新投入分别验证处于不同的条件之下的条件β收敛性状况,其中产业结构用第三产业增加值GDP占比来表示,外贸依存度则表征对外开放程度。根据似然比检验,本文选择恰当的模型进行回归,发现辽西北地区在科技创新投入的作用下,回归方程系数不能通过显著性检验。
辽宁全省、辽东地区、辽中南地区在产业结构、对外开放程度、科技创新投入的作用下和辽西北地区在产业结构、对外开放程度的作用下,均满足了β收敛特征。由此可判断辽宁省各市的工业能源生态效率收敛于各自相同的稳态水平。回归方程中Xi,0的系数ψ决定了变量对工业生态效率的方向,效率稳态通过工业生态效率趋势判断,若是存在收敛,则收敛方向即为发展趋势。

表3 辽宁省工业生态效率β收敛性的影响因素
根据表3可知,辽宁省工业生态效率总体上呈上升态势,由低水平效率向高水平效率收敛,产业结构、对外开放程度和科技创新投入全部促进效率值的提升,因此全部促进向稳态水平趋同;辽东地区同样是高稳态水平,对外开放程度、科技创新投入促进收敛,而产业结构对收敛有消极作用;辽中南地区的收敛方向为效率值由低至高,以及产业结构、对外开放程度。科技创新投入皆为正向促进作用;辽西北收敛方向是由高效率值至低效率值,科技创新投入回归系数不显著,产业结构对效率值起消极作用,与稳态方向一致,而对外开放程度促进效率值的提升,与稳态方向相反。
4 结论与讨论
4.1 结论
本文以辽宁省为例,综合运用熵值法、工业生态效率综合评价模型,计算出辽宁省14个地级市的工业生态效率值。对综合评价指数进行对比研究,利用ArcGIS软件对其进行空间可视化处理,观察工业生态效率值在全省的空间布局和时间序列演化,最终得出以下结论:辽宁省的工业生态效率值总体上较高,地区效率值多以中、高效率值为主,在2000—2014年辽宁省的整体水平呈现出显著提升;空间格局上则主要表现出“中心—外围”结构,沈阳、大连作为辽宁省的“双核”城市,辐射全省的城市发展,对工业生能源态效率的提高起到促进和带动作用。
4.2 讨论
整体来看,尽管全省总体的能源生态效率呈现出上升态势且省内各个区域的差异正在缩小,但全省工业生态效率值不均衡性仍较大,因此对各区域的改进提出以下建议:①辽西北地区最迫切的任务是有效控制工业生态效率的下跌趋势。通过条件β收敛发现,辽西北地区第三产业比重促进稳态发展,却阻碍了工业生态效率的有效提升。一般而言,第三产业能耗低,发展第三产业有利于能源效率的提升,直接促进工业生态效率的发展,但条件β收敛的结论却与这一结论相悖。这种状况,恰恰反映出辽西北地区第二产业比重过于庞大,第三产业发展滞后,多年的粗放型经济增长并未得到根本性的改变。为了从根本上解决工业生态效率低下问题,辽西北地区必须发展新型工业与现代服务业,从节约能源、提高生产率和保护生态环境等多方面入手。②辽东地区在保持稳态水平的基础上要继续实现工业生态效率水平的稳步提升,加大资金投入研发力度,推广环保技术,提升工业生产率,加强环保监管使环保倒逼产业升级与新型工业化的发展,提升自身的开放水平,引进技术与设备,促进工业效率的提升。③辽东地区的工业生态效率在全省处于领先水平,沈阳、大连作为辽宁省经济的增长极和技术创新的核心城市,先进技术的扩散直接导致辽东地区在工业生态效率上优于省内其他区域。今后辽东北地区应当继续推动产业结构改革,持续优化产业结构、大力推进产业升级,提升自身开放水平,与世界先进企业合作交流,发展科技含量高、资源消耗低、环境污染少的新型工业,在做好做强新服务领域下、新服务模式下的现代服务业。
[1]张如波,任胜钢,蔡立燕.长江三角洲城市群工业生态效率评价[J].商业研究,2017,(6)∶163-169.
[3]刘晓萌,孟祥瑞,汪克亮.城市工业生态效率测度与评价:安徽的实证[J].华东经济管理,2016,30(8)∶29-34.
[4]岳强,王鹤鸣,陆钟武.基于总物流分析的我国钢铁工业生态效率分析[J].环境科学研究,2014,27(8)∶915-921.
[5]毛建素,曾润,杜艳春,等.中国工业行业的生态效率[J].环境科学,2010,31(11)∶2788-2794.
[6]何宜庆,陈林心,焦剑雄,等.金融集聚的时空差异与省域生态效率关系研究[J].数理统计与管理,2017,36(1)∶162-174.
[7]汪克亮,孟祥瑞,杨宝臣,等.基于环境压力的长江经济带工业生态效率研究[J].资源科学,2015,37(7)∶1491-1501.
[8]关伟,杜海东,许淑婷,等.辽宁省能源效率测度及其时空分异研究[J].资源开发与市场,2016,32(5)∶556-561,625.
[9]潘兴侠,何宜庆.工业生态效率评价及影响因素研究----基于中国中东部省域面板数据[J].华东经济管理,2014,28(3)∶33-38.
[10]程晓娟,韩庆兰,全春光.基于PCA—DEA组合模型的中国煤炭产业生态效率研究[J].资源科学,2013,35(6)∶1292-1299.
[11]尹科,王如松,周传斌,等.国内外生态效率核算方法及其应用研究述评[J].生态学报,2012,32(11)∶3595-3605.
[12]关伟,许淑婷.辽宁省能源效率与产业结构的空间结构及耦合关系[J].地理学报,2014,69(4)∶520-530.
[13]张馨之,何江.劳动生产率、产业结构与σ收敛—基于珠江三角洲地区9个城市的研究[J].软科学,2012,26(9)∶84-88.
[14]周四军,罗丹.中国能源利用效率β收敛性的区域研究[J].财经理论与实践,2012,38(5)∶118-123.
[15]Adhikari D,Chen Y.Sectoral Analysis of Energy Productivity Convergence:Empirical Evidence from Countries[J].Modern Economy,2014,5(9)∶980-988.
[16]赵楠,王辛睿,朱文娟.中国省际能源利用效率收敛性研究[J].统计研究,2015,32(3)∶29-35.
[17]陈黎明,王颖,田建芳.中国省际能源—经济—环境系统协调性实证研究[J].财经理论与实践,2016,(1)∶105-110.
[18]Meeusen W,Van den Broeck J.Efficiency Estimation from Cobb-douglas Production Function with Composed Error[J].International Economic Review,1977,18(2)∶435-444.
[19]王丽琼.中国能源利用效率区域差异基尼系数分析[J].生态环境学报,2009,18(3)∶974-978.
[20]鹿晨煜,张琳,薛冰,等.辽宁省区域可持续发展时空综合测度研究[J].经济地理,2015,35(8)∶32-39.
[21]盖美,曹桂艳,田成诗,等.辽宁沿海经济带能源消费碳排放与区域经济增长脱钩分析[J].资源科学,2014,36(6)∶1267-1277.
[22]张媛,郝丽莎,杨足膺.江苏省能源效率空间分异特征与成因分析[J].地理学报,2010,65(8)∶919-928.
————不可再生能源

