基于波长平滑算子的逆时偏移回转波假象去除方法

唐永杰 宋桂桥 刘少勇 顾汉明* 严 哲

(①中国地质大学(武汉)地球物理与空间信息学院，湖北武汉 430074； ②地球内部多尺度成像湖北省重点实验室，湖北武汉 430074； ③中国石化油田勘探开发事业部，北京 100728)

1 引言

随着地震勘探目标越来越复杂、越来越精细，基于射线理论和单程波方程理论的地震偏移技术已难以满足业界需求[1-3]； 而采用双程波动方程的逆时偏移(RTM)具有成像精度高、相位准确、适应于变速介质和陡倾构造成像的特点[4，5]，并且可对绕射波、多次波、棱柱波等进行成像[6-8]，因此，RTM已成为目前复杂构造成像的常用方法之一。

RTM方法自20世纪80年代被提出以来[9-11]，主要面临计算效率和偏移假象两大问题的挑战。随着计算机技术的飞速发展以及各种RTM优化算法和并行策略的提出[12-20]，计算效率问题基本得到了解决。针对偏移假象问题，传统相关成像条件中来自炮检点同向传播波场产生的低频噪声受到广泛关注，并涌现出多种消除此类低频噪声的方法。Loewenthal等[21]采用平滑速度方式消除背向散射波场进而压制低频噪声； Mulder等[22]通过带通滤波器对偏移后的成像结果进行滤波处理以消除低频假象； Valenciano等[23]利用反褶积成像条件压制低频噪声； Fletcher等[24]提出采用方向性衰减方法压制层间反射从而去除RTM中的低频假象； Yoon等[25]将Poynting矢量引入成像条件以消除低频噪声进而提高成像质量； Guitton等[26]采用最小平方滤波法去除低频噪声； Liu等[27]先将全波场分解为各自的单程波分量，再选取合适分量进行互相关成像； Zhang等[28]通过切除角度域成像道集中的大角度部分，再做角度叠加，以此压制低频假象； Liu等[29]提出一种基于Hilbert变换的波场分解法，该方法不需将波场显式分解，也不需存储整个波场，只需选择性地对有效成像路径进行互相关从而达到去除低频噪声的目的； Rocha等[30]提出基于能量范数的成像条件来消除低频噪声。

除了常见的低频假象外，当偏移速度梯度较大或反射界面较复杂时，RTM结果中会产生回转波假象，该假象不能像低频噪声那样通过简单的滤波手段去除。Fei等[31]提出可将源、检波场进行分解，仅利用震源波场的下行波与检波点波场的上行波做互相关，从而消除该假象。此类方法采用类似于单程波偏移的成像条件时会对高陡倾构造成像产生一定影响，且震源(检波点)波场的显式分解需在频率—波数域进行，其计算较复杂。

本文引入上、下行波分离成像条件分析RTM中产生假象的原因，认为回转波假象是在强速度梯度带由震源波场上行波与检波点波场下行波互相关产生，进而提出一种基于波长平滑算子的回转波假象去除方法。该方法避免波场分解，通过引入波长平滑算子，使波场在强速度梯度处的传播特征更接近于真实速度中波场传播特性，进而压制回转波假象，因此可较好地兼顾效率和高陡构造成像。

2 RTM中回转波假象成因分析

逆时偏移过程包含炮检波场的正反传播和成像条件施加两部分，其中常用的互相关成像条件可表示为

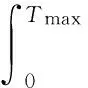
(1)

式中：x为地下成像点位置；t为炮检点传播到成像点的时间；s(t,x)和r(t,x)分别为时、空域炮检点波场；Tmax为最大记录时间；I(x)为成像结果。RTM的实现是基于双程波动算子，故在波场外推时会产生反射波和透射波。Liu等[27]提出将波场进行上、下行波分解，则震源波场s(t,x)可分解为上行波su(t,x)和下行波sd(t,x)，检波点波场r(t,x)可分解为上行波ru(t,x)和下行波rd(t,x)，即炮检点波场可表示为

s(t,x)=su(t,x)+sd(t,x)

(2)

r(t,x)=ru(t,x)+rd(t,x)

(3)

式中 u(上行)和d(下行)代表波的传播方向。将式(2)和式(3)代入式(1)，可得

=I1(x)+I2(x)+I3(x)+I4(x)

(4)

式中：I1(x)表示震源波场下行波与检波点波场上行波互相关成像结果；I2(x)表示震源波场上行波与检波点波场下行波互相关成像结果；I3(x)表示震源波场下行波与检波点波场下行波互相关成像结果；I4(x)表示震源波场上行波与检波点波场上行波互相关成像结果。在当前反射波偏移成像框架下,I1(x)和I2(x)对应震源波场和检波点波场反向传播的波场进行互相关，都可对地下反射界面进行成像。具体而言：I1(x)类似于单程波偏移的成像条件，结果即对应一次反射波成像；I2(x)即对应能量较一次波弱的多次波成像；I3(x)和I4(x)对应震源波场和检波点波场同向传播的波场进行互相关，即表现为低频假象，一般通过拉普拉斯滤波可较彻底地消除。当震源波场和检波点波场通过强速度梯度或复杂反射界面时，将产生向上回传的波场(图1)，此时I2(x)则表现为一次回转波产生的假象，其能量强于多次波成像，且难以被去除。

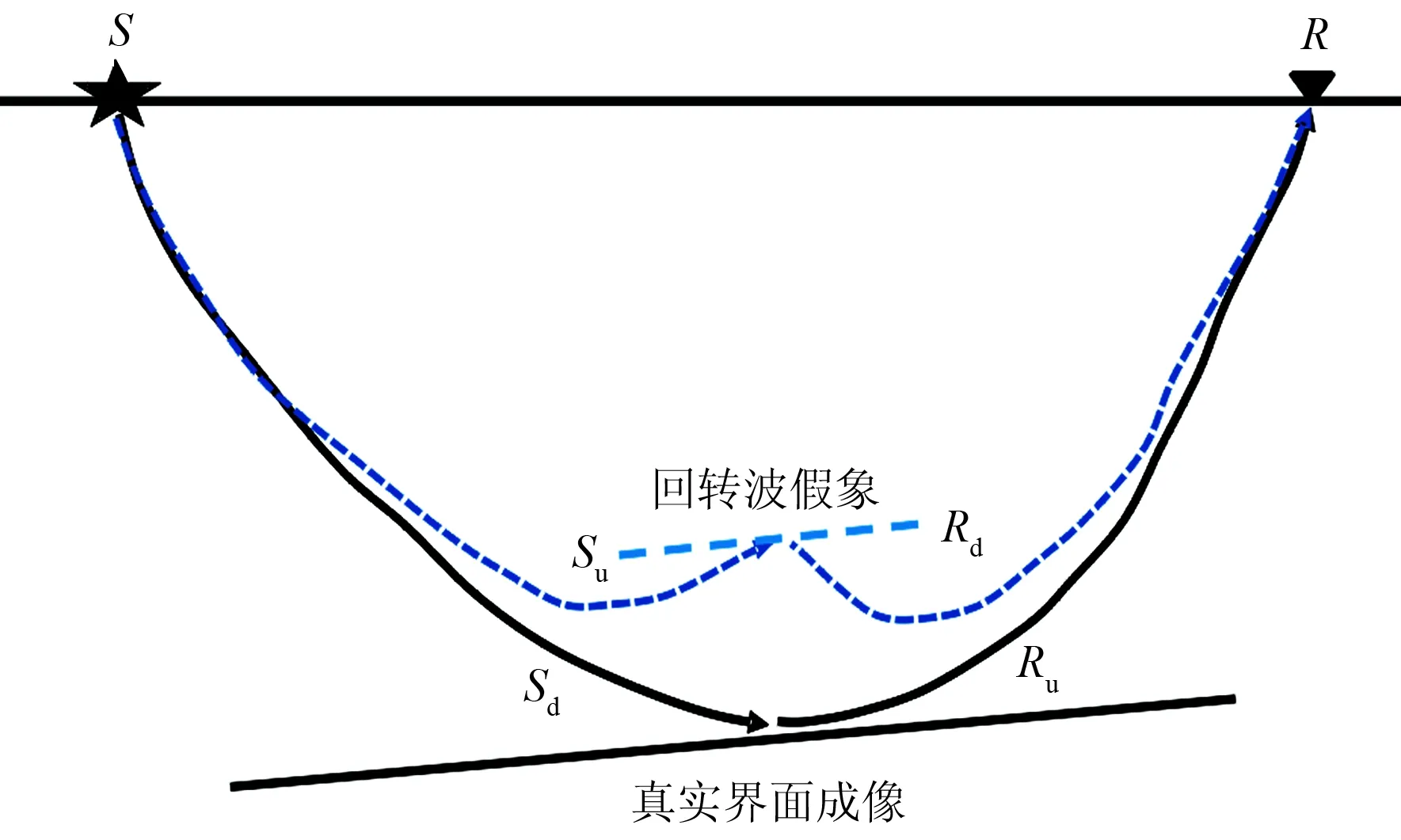
图1 回转波假象产生示意图

为进一步验证该回转波假象是由I2(x)(震源波场上行波与检波点波场下行波互相关结果)分量产生，选取一个两层模型进行测试。模型上、下层速度分别为2000m/s和4000m/s(图2a)，其偏移速度为该两层模型做高斯平滑后速度模型(图2b)。

基于该模型，将震源波场和检波点波场分解为各自的上、下行波，分别选取对应的波场分量进行成像(图3)。图3a表示式(4)中I1(x)和I2(x)相加的成像结果，可见当偏移速度具有较强的速度梯度时，成像结果中真实反射界面上方出现了假的同相轴(红色箭头)； 图3b表示I1(x)震源波场下行波与检波点波场上行波互相关成像结果，对应反射界面的成像； 图3c表示I2(x)震源波场的上行波与检波点波场的下行波互相关成像结果，对比可知I2(x)成像结果即是图3a中回转波假象。

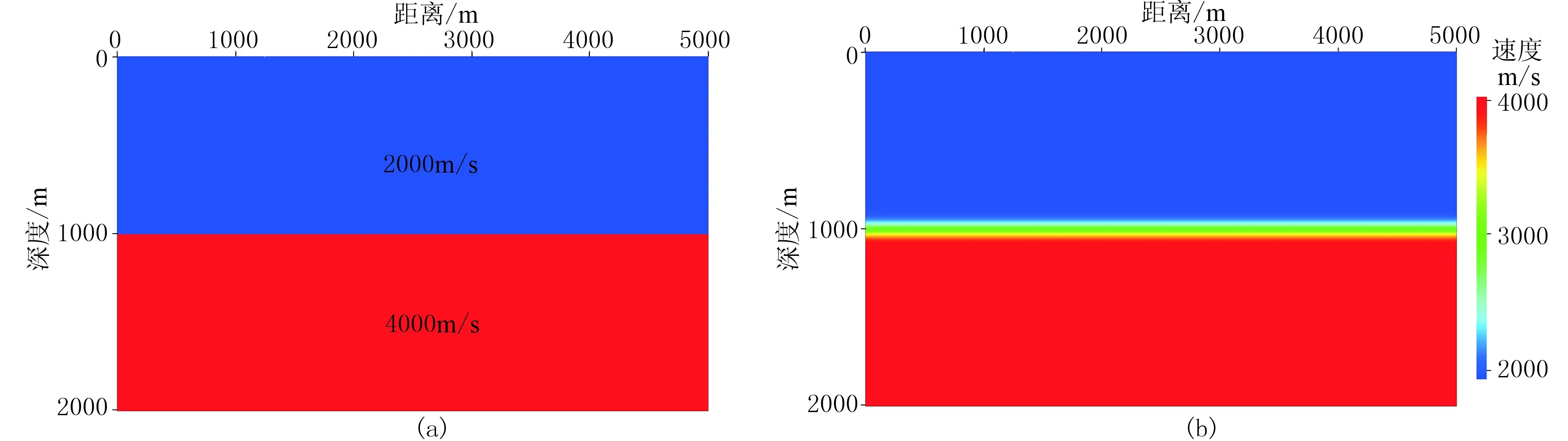
图2 两层介质速度模型 (a)准确速度； (b)高斯光滑速度

图3 采用高斯光滑偏移速度得到的不同分量偏移结果 (a)I1(x)+I2(x)； (b)I1(x)； (c)I2(x)

3 用波长平滑算子去除回转波假象

通过以上分析可知，在采用互相关成像条件进行RTM成像时，在强速度梯度处会产生回转波，相关成像结果表现为类似于一次反射波成像结果的假同相轴，该假象没有典型的低频噪声特征，不能通过简单叠后滤波方法去除。若不考虑多次波成像，且引入波场分解成像条件，仅利用式(4)中I1(x)(震源波场下行波与检波点波场上行波互相关结果)分量成像即可较好地回避此假象[31]。但该方法需对波场进行显式分解，而一般的波场分解法宜在频率—波数域进行，需将整个波场进行存盘，并进行关于时间最慢维的高维傅里叶变换，其计算量和存储量都较大； 另一方面该方法也损失了RTM相对于单程波偏移的优势，因其仅是对波场进行上、下行波分离，则对陡倾角构造的成像有一定的局限性。

在强变速介质中，对速度场做简单平滑(如高斯平滑)会人为引入强速度梯度带而产生回转波，此时常规相关成像条件不能对回转波进行正确成像。如果控制波场在传播过程中只产生符合波传播规律的透射和反射波场，消除回转波，则在互相关成像时该回转波假象就能被压制或消除。基于波长平滑算子的速度平滑法在平滑处理时考虑地震波长因素，使波场更接近于在真实速度中的传播特性，以压制在强速度梯度处产生的向上回传波场，进而压制或消除由此产生的回转波假象。在波长相关平滑中，每一网格点的平均速度为距离该点一个波长内所有点速度的加权平均。对于某一网格点，其波长相关平滑速度为

(5)

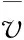
(6)

式中：t表示一个波长内计算网格点到加权点的直线旅行时；T表示对应的周期；p为速度场的维度。

与采用固定窗口的高斯平滑算子相比，本文平滑算子通过引入波长相关的加权函数对速度场进行波长相关平滑，使波场在界面处更符合其物理传播特征。为凸显二者区别，分别采用两种平滑算子对上述两层速度模型进行平滑。图4a～图4c依次对应准确速度、高斯平滑后速度和波长相关平滑后速度纵向变化三种情形。对比发现图4b中界面上下速度梯度一致，而图4c中界面上下速度变化率与波长相关。

为了进一步分析高斯平滑与波长相关平滑对波

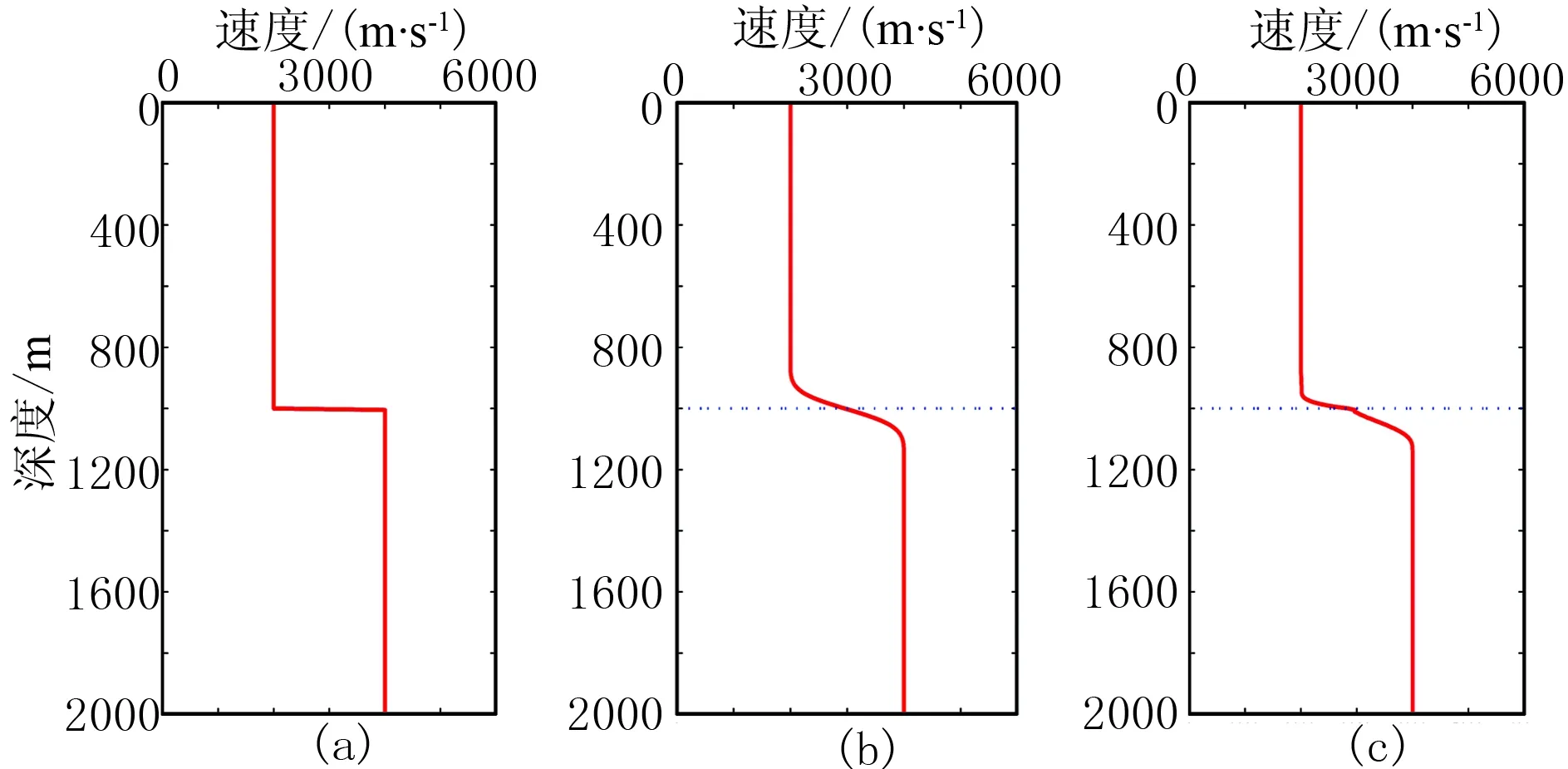
图4 不同速度的纵向变化 (a)准确速度； (b)高斯平滑速度； (c)波长平滑速度

传播的影响，利用有限差分算子针对该模型做波场模拟。图5为采用主频为30Hz震源、以不同平滑速度在不同时刻的波场快照。其中红色虚线代表真实速度模型中波传播的准确旅行时。

通过对比波场快照可见：图5a和图5d中红色虚线与真实速度中的波前面相吻合； 图5b和图5e中高斯平滑速度场的波前较准确时间更快(红色箭头)，这是由于高斯平滑在界面处速度变化率是对称的，波场通过平滑区域所用时间更短；图5c和图5f中波长相关平滑速度场的波前与红色虚线表示的准确旅行时一致，这是由于波长相关平滑考虑了波长因素，平滑后保持了强速度界面变化特征，使波场更接近于准确速度的传播特性，该特性确保不会因平滑而过度降低逆时偏移精度，同时兼顾达到去除回转波假象的目的。

图5 基于不同平滑速度模型的波场快照 (a)、(b)和(c)分别为真实速度、高斯平滑速度和30Hz波长相关平滑速度的0.7s波场快照； (d)、(e)和(f)为对应的0.85s波场快照

从上述试算结果及其分析可知，波长平滑算子能改善地震波在复杂介质中的传播，这是在逆时偏移互相关成像中压制回转波假象的基础。

4 数值算例

采用洼陷模型测试本文提出的波长平滑算子对RTM中回转波假象的去除效果。图6a所示准确速度模型的尺寸为5000m(横)×2000m(纵)。对该模型进行有限差分模拟的参数为：子波是主频为20Hz的雷克子波，道距为10m， 炮检距范围是-5000～5000m，采样间隔为1ms，采样长度为2.5s，炮间距为50m，共101炮。图6b和图6c分别为高斯平滑速度场和20Hz波长平滑速度场。图7a为采用高斯平滑速度获得的RTM成像结果，可见洼陷两侧出现假同相轴(红色箭头)； 图7b为采用20Hz波长平滑速度获得的RTM成像结果，易见洼陷两侧假象已消除。

采用复杂盐丘模型[31]进一步测试本文方法对复杂地质体适用性。图8a所示准确速度模型的尺寸为20km(横)×7.8km(纵)。模型中部为火山岩侵入构造，该盐丘具有不规则边界，其速度高于围岩。对该模型进行有限差分模拟的参数为：子波是主频为20Hz的雷克子波，道距为20m，炮检距范围是-10～10km，采样间隔为4ms，采样长度为10s，炮间距为80m，共251炮。图8b和图8c分别为高斯平滑速度场和20Hz波长平滑速度场。分别采用准确速度场、高斯平滑速度场和20Hz波长平滑速度场进行逆时偏移成像(图9)。在采用准确速度场得到的偏移结果(图9a)中可见盐丘顶部不存在强速度梯度带，不产生回转波，即盐丘顶界面并未产生假象；而在采用高斯平滑偏移速度得到的偏移结果(图9b)中看到盐丘顶部出现了假同相轴(红色箭头)，该假象频带与有效信号频带相近，且不能通过滤波去除； 在采用波长相关平滑速度场得到的偏移结果(图9c)中，可见盐丘顶部回转波假象(相对图9b的高斯平滑速度偏移结果)被消除，这有助于对盐丘边界、潜山面和火成岩边界的地震解释，而且盐丘两侧陡构造成像效果也更好(红色椭圆)；另外，采用波长平滑速度的偏移结果(图9c)在成像精度上并不明显低于准确速度模型成像结果(图9a)。

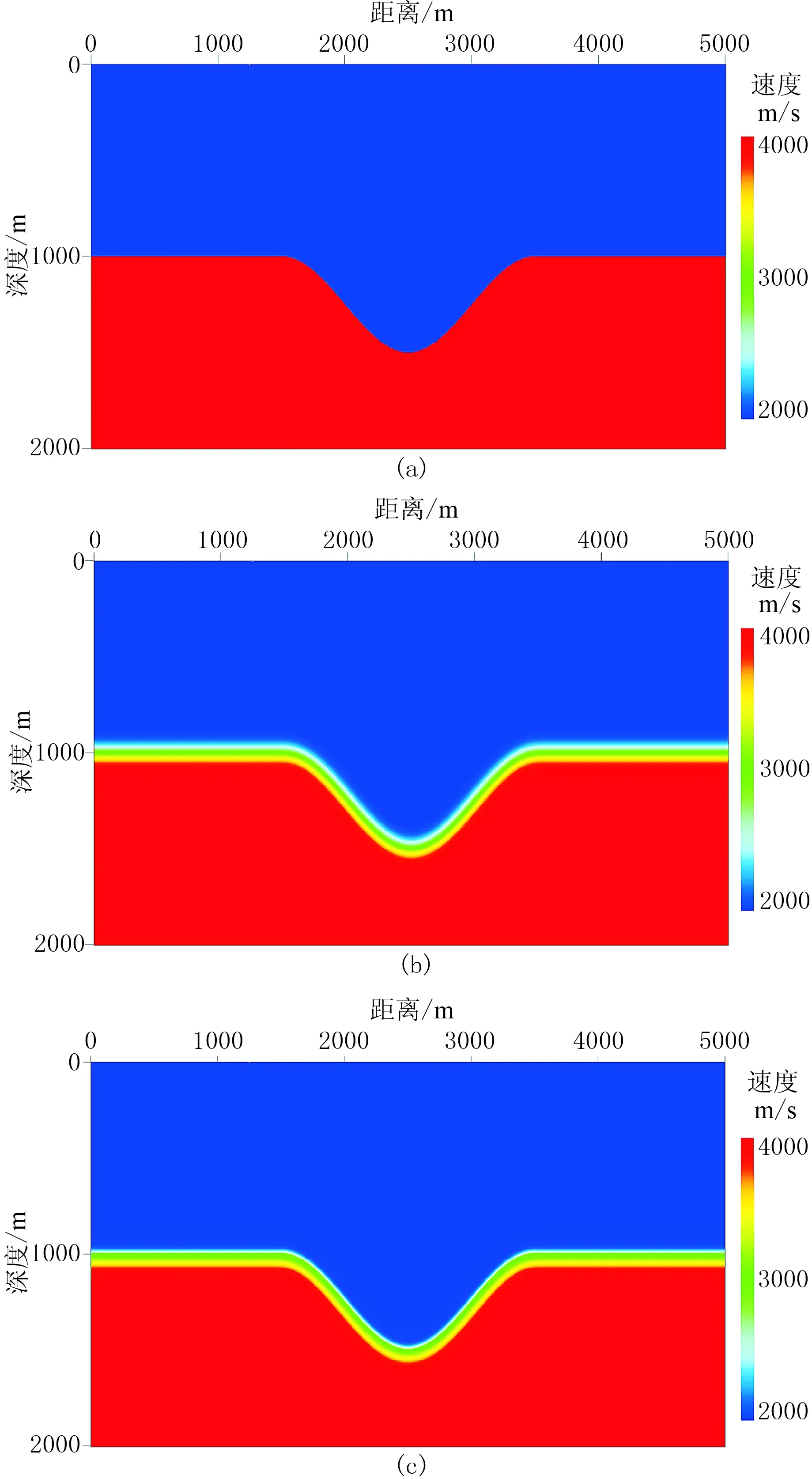
图6 不同速度场的洼陷模型 (a)准确速度场； (b)高斯平滑速度场； (c)20Hz波长平滑速度场

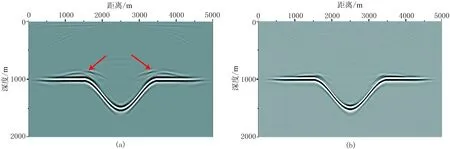
图7 不同偏移速度获得的洼陷模型成像结果 (a)高斯平滑速度； (b)波长平滑速度

图8 不同速度场的盐丘模型 (a)准确速度场； (b)高斯平滑速度场； (c)20Hz波长平滑速度场

5 结论与讨论

在地下强速度梯度区域，基于互相关成像条件的RTM会产生回转波假象，该假象区别于典型的低频噪声，有较强的能量且不容易去除。本文通过波场分解成像条件分析回转波假象产生原因，认为该假象是缘于震源波场上行波与检波点波场下行波的互相关，即强梯度带的回转波在传统相关成像条件下产生。据此提出一种基于波长平滑算子的回转波假象去除方法：通过波长相关平滑算子进行速度平滑，在波传播过程中压制回转波的产生，进而消除回转波假象。该方法区别于通过波场分解法消除回转波成像假象，可以很好地对高陡构造进行成像且不增加RTM的计算复杂度。

[1] Yoon K，Marfurt K J，Starr W.Challenges in reverse-time migration.SEG Technical Program Expanded Abstracts,2004，23：1057-1060.

[2] Zhu J，Lines L R.Comparison of Kirchhoff and reverse time migration methods with application to prestack depth imaging of complex structures.Geophysics，1998，63(4)：1166-1176.

[3] Sava P，Hill S J.Overview and classification of wavefield seismic imaging methods.The Leading Edge，2009，28(2)：170-183.

[4] 杨午阳，张厚柱，撒利明等. 逆时偏移关键问题探讨. 石油地球物理勘探，2016，51(6)：1251-1262. Yang Wuyang，Zhang Houzhu，Sa Liming et al.Some issues about reverse time migration.OGP，2016，51(6)：1251-1262.

[5] 王鹏飞，何兵寿.基于行波分离的三维弹性波矢量场点积互相关成像条件.石油地球物理勘探，2017，52(3)：477-483. Wang Pengfei，He Bingshou.Vector field dot product cross-correlation imaging based on 3D elastic wave separation.OGP，2017，52(3)：477-483.

[6] 叶月明，郭庆新，孙小东等.多次波对逆时偏移构造成像的影响.石油地球物理勘探，2014，49(3)：523-529. Ye Yueming，Guo Qingxin，Sun Xiaodong et al.Multiples influence on structure imaging in reverse time migration.OGP，2014，49(3)：523-529.

[7] Deeks J，Lumley D.Prism waves in seafloor canyons and their effects on seismic imaging.Geophysics，2015，80(6)：S213-S222.

[8] Weglein A B.Multiples：Signal or noise? Geophysics，2016，81(4)：V283-V302.

[9] Whitmore D N.Iterative depth migration by backward time propagation.SEG Technical Program Expanded Abstracts，1983，2：382-385.

[10] Baysal E，Kosloff D D，Sherwood J W C.Reverse time migration.Geophysics，1983，48(11)：1514-1524.

[11] McMechan G A.Migration by extrapolation of time-dependent boundary values.Geophysical Prospecting，1983，31(3)：413-420.

[12] Fricke J R.Reverse-time migration in parallel：A tutorial.Geophysics，1988，53(9)：1143-1150.

[13] Harris C E，McMechan G A.Using downward continu-ation to reduce memory requirements in reverse-time migration.Geophysics，1992，57(6)：848-853.

[14] Symes W.Reverse time migration with optimal check-pointing.Geophysics，2007，72(5)：SM213-SM221.

[15] 刘红伟，李博，刘洪等.地震叠前逆时偏移高阶有限差分算法及GPU实现.地球物理学报，2010，53(7)：1725-1733. Liu Hongwei，Li Bo，Liu Hong et al.The algorithm of high order finite difference prestack reverse time migration and GPU implementation.Chinese Journal of Geophysics，2010，53(7)：1725-1733.

[16] Anderson J E，Tan L，Wang D.Time-reversal check pointing methods for RTM and FWI.Geophysics，2012，77(4)：S93-S103.

[17] 张慧，蔡其新，秦广胜等.基于GPU并行加速的逆时偏移成像方法.石油地球物理勘探，2013，48(5)：707-710. Zhang Hui，Cai Qixin，Qin Gunagsheng et al.GPU-accelerated reverse time migration and its application.

OGP，2013，48(5)：707-710.

[18] 唐祥功，匡斌，杜继修等.多GPU 协同三维叠前逆时偏移方法研究与应用.石油地球物理勘探，2013，48(6)：910-914. Tang Xianggong，Kuang Bin，Du Jixiu et al.3D pre-stack reverse time migration based on multiple-GPU collaboration.OGP，2013，48(6)：910-914.

[19] Clapp R G.Seismic processing and the computer revolution.SEG Technical Program Expanded Abstracts，2015，34：4832-4837.

[20] Yang P，Brossier R，Virieux J.Wavefield reconstruction by interpolating significantly decimated boundaries.Geophysics，2016，81(5)：T197-T209.

[21] Loewenthal D，Stoffa P L，Faria E L.Suppressing the unwanted reflections of the full wave equation.Geophysics，1987，52(2)：1007-1012.

[22] Mulder W，Plessix R.One-way and two-way wave-equation migration.SEG Technical Program Expanded Abstracts,2003，22：881-884.

[23] Valenciano A，Biondi B.2D deconvolution imaging condition for shot-profile migration.SEG Technical Program Expanded Abstracts，2003，22：1059-1062.

[24] Fletcher R，Fowler P，Kitchenside P.Supressing unwanted internal reflections in prestack reverse-time migration.Geophysics，2006，71(6)：E79-E82.

[25] Yoon K，Marfurt K J.Reverse-time migration using the poynting vector.Exploration Geophysics，2006，37(1)：102-107.

[26] Guitton A，Kaelin B，Biondi B.Least-square attenuation of reverse-time migration artifacts.SEG Technical Program Expanded Abstracts，2006，25：2348-2352.

[27] Liu F，Zhang G Q，Morton S A.Reverse-time migration using one-way wavefield imaging condition.SEG Technical Program Expanded Abstracts，2007，26：2170-2174.

[28] Zhang Y，Sun J.Practical issues of reverse time mi-gration：true amplitude gathers，noise removal and harmonic-source encoding.ASEG Extended Abstracts，2009，1-5.

[29] Liu F，Zhang G Q，Morton S A et al.An effective imaging condition for reverse-time migration using wavefield decomposition.Geophysics，2011，76(1)：S29-S39.

[30] Rocha D，Tanushev N，Sava P.Acoustic wavefield imaging using the energy norm.Geophysics，2016，81(4)：S151-S163.

[31] Fei T W，Luo Y，Yang J et al.Removing false images in reverse time migration：The concept of de-primary.Geophysics，2015，80(6)：S237-S244.