TBCC飞行器发动机尺寸选型及爬升策略设计

李 乐, 姜光泰, 褚显应, 王 健

(北京机电工程研究所，北京 100074)

0 引 言

高度在20～100 km的空间被称为临近空间，伴随着动力技术和控制技术的发展，临近空间高速飞行器成为大国争相发展的热点装备。该类飞行器要实现远程飞行，需尽量降低爬升段油耗，提高巡航段升阻比和比冲。为此，气动外形与动力系统匹配设计以及爬升策略选择是关键。一方面，临近空间高速飞行器动力系统通常选用涡轮冲压组合(Turbine Based Combined Cycle, TBCC)发动机[1]，内外流耦合作用明显，研究发动机尺寸选型对巡航航程的影响非常重要。另一方面，临近空间高速飞行器爬升段高度变化大，加速性能要求高，采用TBCC发动机易出现高空推力不足问题，可考虑采用固体火箭助推器在适当时机辅助加速爬升，为巡航段剩余更多燃油。

近年来，国内利用伪谱法开展临近空间飞行器航迹优化的研究有很多[2-4]。基于伪谱法研究TBCC发动机尺寸与飞行器适配性和助推器与飞行器的适配性问题的研究较少。

本文拟通过hp自适应Radau伪谱法，以消耗燃料质量最小为目标优化航迹，研究TBCC发动机尺寸选型和固体火箭助推器质量、推力、点火时刻、工作时间等因素对临近空间高速飞行器爬升航迹和巡航航程的影响。以此为基础，提出一种TBCC发动机尺寸选型的依据和固体火箭助推器辅助加速的爬升策略。为未来临近空间高速飞行器发动机尺寸选型和选用固体火箭助推器提供参考。

1 临近空间高速飞行器模型

本文设计了一型临近空间高速飞行器。其设计条件为：巡航高度25 km，巡航马赫数3.5。动力系统采用串联式涡轮冲压组合(TBCC)发动机。经过设计计算，飞行器气动外形如图1所示。飞行器基本外形和质量参数如表1所示。

2 航迹优化数学模型

研究临近空间高速飞行器航迹优化问题，需要建立动力学模型、大气模型、发动机模型和气动力模型。

2.1 动力学模型

忽略地球自转影响，考虑地球曲率，只研究飞行器纵向平面内运动，建立的动力学模型如式(1)。

(1)

式中r=Re+h，h为飞行高度，Re为地球半径，v为飞行速度，m为飞行器质量，θ为航迹倾角，T为发动机推力，ms为发动机耗油率，k为伪控制量，D为阻力，L为升力，α为迎角，μ为地球引力常数。

2.2 发动机模型

本文设计的临近空间高速飞行器采用串联轴对称涡轮冲压组合发动机(TBCC)提供推力，组合发动机原型的推力和耗油率数据参考J-58发动机[5-7]得到，与高度、来流马赫数和迎角相关。0度迎角下，发动机推力和耗油率随飞行高度和速度的变化规律如图2所示。来流Ma3.5时，不同高度发动机推力和耗油率随迎角变化规律如图3所示。

2.3 大气模型

大气模型采用1976年美国标准大气模型，依据高度插值得到声速和空气密度。

2.4 气动力模型

飞行器飞行过程中受到的升力、阻力计算公式如式(2)和式(3)。

(2)

(3)

式中:S为参考面积，即为机翼投影面积，ρ为大气密度，v为飞行速度，CL和CD分别为升力系数和阻力系数，是迎角α和马赫数M的函数，其利用Digital DATCOM[8]计算得到，如图4所示。

2.5 约束条件

(1)爬升段初末状态约束

表2 爬升段初末状态列表Table 2 The initial and final states of ascent trajectory

(2)爬升段路径约束

在吸气式组合动力飞行器爬升过程中，约束航迹倾角以保证足够的推阻余量；约束迎角以保证发动机进气量和进气道启动；迎角变化率约束主要考虑飞行器法向过载约束；飞行器发动机可靠工作、翼面载荷和舵面铰链力矩要求对最大动压予以约束；头部驻点热流密度也需要约束以满足飞行器热防护系统要求。

航迹倾角约束：-40°≤θ≤40°,

迎角约束：-5°≤α≤10°,

伪控制量约束：0≤k≤1,

法向过载约束：

(4)

头部驻点热流约束：

(5)

最大动压约束：

(6)

分析仿真结果得到主要约束条件是航迹倾角约束、迎角变化率约束和伪控制量约束。

(3)巡航段初末状态及路径约束

巡航段初始条件即是爬升段末端条件，巡航段的末端条件设为飞行器剩余5%油量(用于降落)。巡航段路径约束条件为：

h=25 km，Ma=3.5，θ=0°。

3 航迹优化问题求解

针对最优控制问题，本文采用Radau伪谱法求解。该方法在一组Legendre-Gauss-Radau(LGR)点上构造全局Lagrange插值多项式，近似状态变量和控制变量，用插值多项式导数近似微分方程中状态变量的导数，将最优控制问题转化为非线性规划问题[9-10]，再通过序列二次规划(Sequential Quadratic Programming,SQP)算法[11]对其进行求解。

基于hp自适应Radau伪谱法汲取了全局伪谱法和网格细分法的优点，采用双层优化策略，具有更合理的LGR点分布，在保证优化精度的前提下有效提高了算法的优化效率。其基本思想是检验各区间内的相对误差，若超出规定值，则采用细化区间或增加区间内LGR点个数来提高优化精度；而相对误差小于规定值的区间则保持不变[12-13]。这样只需在个别区间细化网格，增加采样密度，从而在满足精度要求的情况下，有效提高了优化速度。基于hp自适应Radau伪谱法的流程框图如图5所示。

4 TBCC发动机尺寸选型

TBCC发动机作为动力系统对飞行器的飞行性能有重要影响。本节讨论TBCC发动机尺寸选型对临近空间高速飞行器爬升航迹和巡航航程的影响。

首先，本文参考J-58发动机建立的基准TBCC发动机主要参数如表3所示。

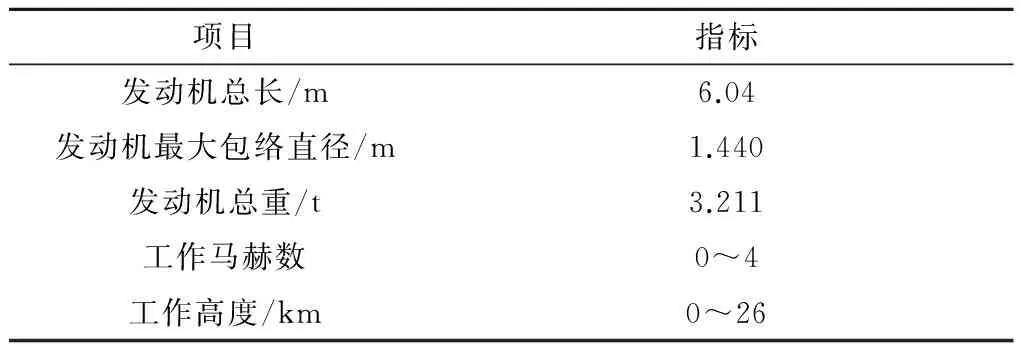
表3 基准TBCC发动机主要参数列表Table 3 Parameters of basic TBCC engine

在方案论证阶段，发动机性能参数主要依靠估算得到。由于可供参考的TBCC发动机型号有限，因此本文通过应用经验和参考相关型号参数，得到如下近似拟合公式：

T=T0·K2

(7)

(8)

发动机质量遵从如下变化规律

m=m0·K1.35

(9)

不同尺寸发动机主要通过三种途径影响爬升航迹。首先，不同尺寸发动机的推力不同；其次，不同尺寸发动机的质量不同，飞行器起飞总重不变条件下，发动机质量变化会影响飞行器载油质量，如表4所示；最后，发动机的直径不同，引起的气动力也不同。为考察爬升段内发动机尺寸对飞行器气动力的影响，本文进行了大量仿真计算。这里选取两个典型状态展示其影响，分别是模态转换起始时(Ma2)和迎角为0.5°时的情况，讨论不同尺寸发动机对飞行器气动力影响随迎角和马赫数的变化规律，结果如图6～7所示。

观察图6～7，一方面，可以发现发动机尺寸对飞行器升力系数的影响较小，对阻力系数影响较大；另一方面，发动机尺寸对飞行器气动力的影响随马赫数变化较为敏感，且对爬升过程中的阻力峰值影响较大。在不同迎角下，发动机尺寸增大导致飞行器的升力和阻力同时增加。但发动机尺寸对飞行器气动力的影响随马赫数的变化则不规律。

表4 不同尺寸发动机的直径和质量列表Table 4 Diameter and mass of different size of TBCCengines

本文以所设计的临近空间高速飞行器为原型，基于第2节建立的航迹优化数学模型，代入不同尺寸TBCC发动机，依据优化得到的控制变量变化规律，仿真得到爬升航迹参数变化曲线如图8～11所示，其中K为发动机直径比。

通过图8～9可以看出，当采用较小尺寸发动机时，飞行器高度爬升有迟滞，甚至有俯冲加速的趋势；当采用较大尺寸发动机时，飞行器可以直接爬升到巡航高度，但速度爬升末段存在迟滞，甚至有减速爬升的趋势。其原因是为减小爬升段消耗燃料，如图10所示飞行器在相应阶段燃料消耗率明显降低。图11显示配备大尺寸发动机的飞行器在转平阶段短时间内有负迎角，且发动机尺寸越大负迎角度数和持续时间也越长。随着发动机尺寸变大，飞行器爬升消耗燃料质量减小。但飞行器爬升航迹趋于一致，反映在爬升消耗燃料质量趋同，如图12所示。

图13比较了配备相同尺寸发动机的飞行器，分别以爬升消耗燃料质量最小和爬升所用时间最小为目标优化得到的结果，两种目标优化得到的航迹，其所用时间和爬升消耗燃料质量差值随发动机尺寸增大而减小。这说明较大尺寸发动机可以近似同时满足爬升最快和最省燃料的要求。

接下来讨论不同尺寸发动机对巡航航程的影响。首先，相同尺寸发动机和巡航飞行条件一定情况下，爬升消耗燃料质量越小，意味着有更多燃料可供巡航飞行，因而爬升消耗燃料质量越小，飞行器巡航航程越大。以此为基础开展飞行器巡航段仿真。

本文将飞行器需用推力与此环境下飞行器可用推力之比定义为发动机推力利用率。仿真结果图14显示，随着发动机尺寸增大，巡航段推力利用率逐步降低，即过大尺寸发动机会导致巡航推力的较大浪费，且会导致较大的飞行阻力和减小飞行器所载燃料质量，不利于提升航程。

由图15可看出，巡航起始点升阻比随发动机尺寸增大先增大后减小，巡航航程与巡航起始点升阻比的变化趋势基本一致，说明影响巡航航程的主要因素仍是巡航升阻比。综上所述，TBCC飞行器的动力系统尺寸匹配问题应综合考虑爬升和巡航段要求，虽然大尺寸发动机在爬升阶段可缩短时间和节省燃料，但会造成巡航段推力利用率低。对于远程飞行器，发动机尺寸选型应主要考虑其对飞行器巡航升阻比的影响。

吸气式组合动力飞行器的爬升方法常采用等动压爬升和等热流密度爬升方法。本文基于1.291倍尺寸发动机，通过将动压关于高度积分后得到爬升平均动压qaver，如式(10)。

(10)

式中qe为飞行过程中来流动压，h0为起始点高度，hf为巡航点高度。基于参考文献[14]方法生成qaver的等动压爬升航迹如图16所示。进一步研究发动机尺寸选型对等动压爬升航迹与优化航迹偏差的影响，结果如图17所示。

通过观察图16和图17可以发现存在最优尺寸发动机，其以爬升消耗燃料质量最少为目标的优化航迹可以部分近似表示为等动压爬升航迹，这为解析表示最优航迹创造了条件。

5 爬升段助推器选型研究

通过分析上节结果可知，TBCC发动机尺寸选型在满足最优巡航升阻比条件下存在巡航状态推力余量较大的问题。为获取最大航程，需要尽量提高巡航起始点推力利用率。这是一个多点设计问题，其实质是受限于涡扇和冲压发动机工作特性，飞行器与TBCC发动机在起飞、爬升和高空巡航阶段难以完全匹配。为此，本文提出一种折衷方案，即考虑在爬升段采用固体火箭助推器辅助加速，以提升飞行器爬升后剩余质量，提高巡航段起始点推力利用率。

经过分析，固体火箭助推器潜在使用阶段包括：起飞阶段，爬升阶段和转平阶段。在起飞阶段使用固体火箭助推器可快速脱离稠密大气，减小飞行阻力；在爬升阶段使用固体助推器有利于飞行器快速通过跨声速阻力峰值；在转平阶段使用固体助推器有助于缓解TBCC发动机高空爬升动力不足的问题。

针对如上助推器的三种使用方案，本文以爬升段最省燃料为目标，选取助推器质量、装药质量流量和点火时刻作为优化变量。动力系统采用1.155倍尺寸TBCC发动机。采用内外两层优化循环，内层循环采用Radau伪谱法对爬升航迹优化，相关状态变量、控制变量约束和路径约束同之前仿真条件。外层循环依据内层优化得到的爬升消耗燃料质量，采用梯度算法优化得到优化变量取值。具体优化框图如图18所示。

采用两枚助推器，在飞行器上挂载示意图如图19所示。飞行器起飞总重保持不变，爬升消耗燃料质量包括助推器质量。并且考虑加装助推器对飞行器气动性能的影响。

固体火箭助推器的其余参数由式(11-13)推导得到：

(11)

(12)

(13)

表5 固体火箭发动机不同高度性能列表Table 5 Performance of solid rocket booster in variable altitudes

助推器装药燃烧速率取为40 mm/s，装药密度取为1.78 g/cm3。单枚助推器总质量为2.5吨情况下，不同装药质量流量对应的助推器外形参数如表6所示。

表6 助推器不同装药质量流量对应的助推器外形Table 6 Appearance feature of solid rocket booster of different fuel flow rate

助推器燃后抛离，因而在助推段与下一段的质量连接条件如式(14)所示。

m2f-m30=0.12mz

(14)

本文设计飞行器在Ma1.5左右阻力较大，图21显示优化得到的助推器工作马赫数主要覆盖这一区间，因而助推器的主要作用是克服爬升过程中的阻力峰值。图22显示配备越大推力的固体火箭助推器对巡航航程的提升作用越大。

接下来讨论三种使用阶段固体火箭助推器的作用效果，结果如表7所示。

通过观察表7可得出如下结论：在爬升不同阶段均倾向于使用大推力固体火箭助推器。在爬升克服阻力峰值时使用助推器节省燃料效果最明显，在起飞阶段使用助推器的效果稍差，在转平阶段使用助推器会增加爬升所需燃料。其原因是在相同装药质量下，大推力固体火箭助推器能在较短时间内将飞行器助推至较高高度，有利于减小气动阻力，节省燃料；大推力助推器可助推飞行器快速通过阻力峰值，减小阻力冲量；在转平段使用固体助推器由于点火时刻较晚，助推器带来的阻力增量作用于全部爬升段航迹，阻力增量做功抵消了助推器做功，因而在转平段使用助推器反而会增加爬升所需燃料。

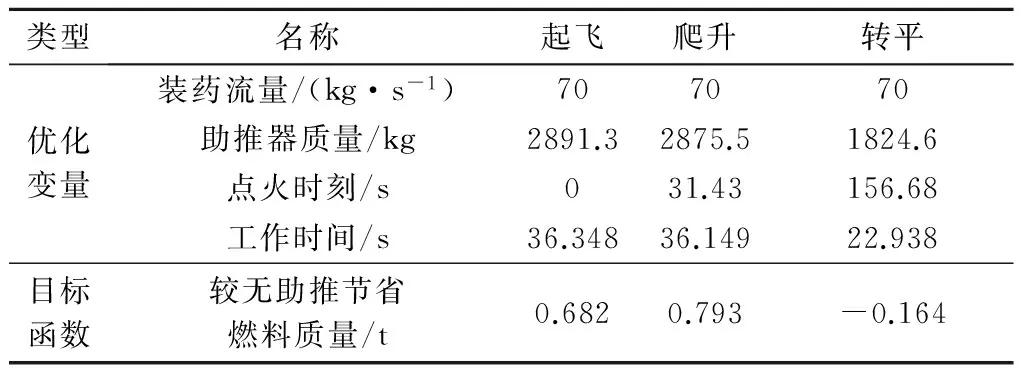
表7 不同飞行阶段优化得到的助推器参数及其影响Table 7 Optimized performance of solid rocket booster in different ascent phases

基于以上分析结果，本文提出一种采用固体火箭助推器辅助加速的爬升策略，首先采用固体火箭助推器辅助加速可以提升飞行器巡航段推力利用率。在对飞行器气动性能影响较小的情况下，选用大质量、大推力的固体火箭助推器，在飞行器阻力峰值附近点火加速的效果最好。

6 结 论

本文设计了一型临近空间高速飞行器，基于hp自适应Radau伪谱法开展爬升段航迹优化，分析了TBCC动力系统尺寸选型和选用固体火箭助推器辅助加速策略对飞行器爬升段航迹和巡航航程的影响。基于分析结果，首先提出TBCC飞行器动力系统尺寸选型的依据，应综合考虑动力需求和对巡航配平升阻比的影响，对于远程飞行器应重点考虑尺寸选型对配平升阻比的影响；其次证明了爬升段采用固体火箭助推器加速爬升策略可以提高飞行器巡航段推力利用率，增大航程。在飞行器阻力峰值附近采用大质量、大推力的固体火箭助推器辅助加速的效果最好。

[1] 王巍巍, 李丹,曾军.国外水平起降临近空间高速飞机动力的发展[J]. 燃气涡轮试验与研究, 2014, 27(1):57-62. [Wang Wei-wei, Li Dan, Zeng Jun. Development of propulsion system for near-space HTHL high-speed vehicles abroad [J].Gas Turbine Experiment and Research, 2014, 27(1):57-62.]

[2] 龚春林,韩璐,谷良贤.适应于RBCC运载器的轨迹优化建模研究[J]. 宇航学报，2013，34(12):1592-1598.[Gong Chun-lin, Han Lu, Gu Liang-xian. Research on modeling of trajectory optimization for RBCC-powered RLV [J]. Journal of Astronautics, 2013, 34(12):1592-1598]

[3] 明超,孙瑞胜,白弘阳,等.吸气式超声速导弹爬升段多约束轨迹优化[J].宇航学报,2016,37(9):1063-1070.[Ming Chao, Sun Rui-sheng, Bai Hong-yang, et al. Climb trajectory optimization with multiple constraints for air-breathing supersonic missile[J]. Journal of Astronautics,2016,37(9):1063-1070.]

[4] 刘瑞帆,于云峰,闫斌斌.基于改进hp自适应伪谱法的高超声速飞行器上升段轨迹规[J], 西北工业大学学报,2016,34(5):790-797.[Liu Rui-fan, Yu Yun-feng, Yan Bin-bin. Ascent phase trajectory optimization for hypersonic vehicle based on hp-adaptive pseudospectral method[J].Journal of Northwes-tern Polytechnical University, 2016,34(5):790-797]

[5] James D. H. Exhaust emission calibration of two J-58 afterburning turbojet engines at simulated high-altitude, supersonic flight conditions[R]. Washington D. C.: National Aeronautics and Space Administration, February 1976.

[6] James D. H. Measurement of exhaust emissions from two J-58 engines at simulated supersonic cruise flight conditions[R]. Washington D. C.:National Aeronautics and Space Administration, March 1976.

[7] David H C. F-12 series aircraft propulsion system performance and development[C], AIAA 5thAircraft Design, Flight Test and Operations Meeting, ST. Louis, USA, August 6-8, 1973.

[8] Mc Donnell Douglas Astronautics Company. The USAF stability and control digital DATCOM, volume I, user’s manual[R]. Missouri: McDonnell Douglas Astronautics Company, April 1979.

[9] Divya G, Michael P, William W. H, et al. A unified framework for the numerical solution of optimal control problems using pseudospectral methods[J], Automatica, 2010,46(11): 1843-1851.

[10] Han P, Shan J Y. Re-entry trajectory optimization using radau pseudospectral method [J]. Control Theory & Applications, 2013, 30(8): 1027-1032.

[11] Philip E.G, Walter M, Michael A.S. SNOPT: an SQP algorithm for large-scale constrained optimization[J], SIAM Journal on Optimization, 2002, 12(4):979-1006.

[12] Michael A P, Anil V R.Exploiting sparsity in direct collocation pseudospectral methods for solving optimal control problems[J], Journal of Spacecraft and Rockets, 2012, 49(2): 364-377.

[13] 雷虎民, 刘滔，李炯,等. 网格缩减的自适应hp伪谱法 [J]. 控制理论与应用 2016, 33(8): 1061-1067.[Lei Hu-min, Liu Tao, Li Jiong, et al. Adaptive mesh refinement of hp pseudospectral method using mesh size reduction [J].Control Theory & Applications, 2016, 33(8)：1061-1067.]

[14] 贾晓娟, 闫晓东. 吸气式组合动力飞行器爬升轨迹设计方法研究 [J]. 西北工业大学学报, 2015, 33(1): 104-109. [ Jia Xiao-juan, Yan Xiao-dong. Ascent trajectory design method for air-breathing powered propulsion system [J]. Journal of Northwestern Polytechnical University, 2015, 33(1)：104-109.]