不同水头与流量条件下堤防梯形决口水流特性数值模拟

曾秀娟，谢 涛

(1.江西省上饶市水利电力勘测设计院，江西 上饶 334000；2.江西省赣州市水利电力勘测设计研究院，江西 赣州 341000)

堤防是世界上最早广为采用的一种重要防洪工程，是防洪体系中重要的挡水建筑物。堤防给人们带来了巨大的经济效益和社会效益，但因漫溢、冲刷、渗透、凌汛、超标准洪水等原因造成堤防决口时，也会带来巨大的损失。在众多洪水险情中，堤防决口是损失最严重、影响面最大、抢险最艰难的[1]。在堤防决口后，若能迅速制定有效的相关封堵决口措施，将大大减少决口造成的损失。通过对堤防决口进行不同工况下的模拟、研究，得到堤防决口处的流速、水面线等水力学特性的分布和变化规律，从而针对性的制定有效的封堵方法，具有重要的意义。近年来，已有部分堤防决口的数值模拟研究成果：李火坤，邓冰梅等[2]对不同决口口门形状下的堤防决口水流建立了三维数值模型；李火坤、曾智超等[3]对堤防决口采用立堵法、平堵法的封堵方法进行数值模拟，得到封堵过程中决口附近的水位场和流速场分布规律；罗娜、刘成林等[4]对不同型式下堤防决口的冲刷过程进行了数值模拟。本文采用FLOW-3D软件以某实际河道堤防为模型，建立了不同水头(6 m、7 m、8 m、9 m)、不同流量(400 m3/s、600 m3/s、800 m3/s、1 000 m3/s和1 500 m3/s)作用下的堤防决口三维数值模拟，得到4种不同水头、5种不同流量下的决口处水流的水力学特性，为拟定有效的决口封堵方案提供科学依据和技术参考。

1 FLOW-3D软件基本介绍

1.1 FLOW-3D软件

FLOW-3D是一款计算流体力学的软件，近年来在水利方面已有较广泛的应用[2-6]，它采用独创的FAVOR(结构化矩形网格)方法及真实的Tru-VOF(可视化)方法[7]，可以模拟真实世界中物理模型的流动现象及准确计算出各种流场性质，特别是自由液面的流动[2]。本文计算模型选择：非恒定模型，VOF模型和RNG湍流模型。

1.2 基本方程

基本方程主要包括连续性方程和动量方程[2-4]。

连续方程式：

(1)

动量方程式：

(2)

(3)

(4)

式中：RDIF为密度扩散；U=(u，v，w)为液体速度，m/s；P为压力，kPa；G为重力和非惯性力加速度，m/s2；τ为粘性应力张量；K为阻力、拖曳力，kN；RSOR为在流速为零的时刻由于大量的注射剂引起的加速度，m/s2；F为其它力(包括表面张力、电场力、动力来源、粒子及用户自定义的力)，kN。

1.3 自由表面处理技术

FLOW-3D软件中自由液面是指具有液气共存的介面模型，在气体中的压力梯度及剪应力是忽略的，通常应用于密度比高达1 000∶1的两种流体。FLOW-3D中自由液面的简化模型：(1)忽略气体流动，气体仅有一个正向压力作用于液体表面上；(2)自由表面上的气体以压力边界取代。FLOW-3D软件采用VOF 法对自由表面进行追踪。 对于水气二相流而言，其基本思想是：定义函数αω(x，y，z，t)和αa(x，y，z，t)分别代表计算区域内水和气占计算区域的体积的相对比例。αω=1，表示该单元完全被水充满；αω=0，表示该单元完全被气充满；αω<1，表示该单元部分是水，部分是气，有自由面。

2 模拟验证

本文选用有较大模拟结果的文献[8]中的一个有矩形障碍物的溃坝算例进行验证。模型尺寸为500 m×300 m×10 m，网格划分为2 m×2 m×1 m，网格总数为3.75×105个。算例给定初始条件为上下游初始水位分别为10 m、5 m，坝中间缺口处水位为0。物理边界条件：重力Z方向给定一个重力加速度，x、y方向不做设置；模型的顶部和上下游边界都设为压力边界条件，左右两侧和底部边界都设定为固壁边界。求解时间设为40 s，时间间隔设为0.5 s。模型平面尺寸见图1所示。

图2从左往右依次是FLUENT[8]、Wang[9]、FLOW-3D的计算时间分别为12 s、18 s、32 s的速度场计算结果。由图可知，FLOW-3D的模拟计算成果与其他两个文献的结果非常相似：在12 s时刻，洪水都未到达矩形障碍物；在18 s时刻，洪水刚到达障碍物；在32 s时刻，洪水波到达下游边界并对矩形障碍物形成绕流，在模型的下游范围内水面相互交叉重叠，从图中可以清楚的看到波的反射和波与波之间的相互作用。通过以上分析可知，用FLOW-3D所建的数值模型计算成果与该算例的其他成果比较吻合，验证了Flow-3D软件用于堤防决口三维数值模拟的可行性。

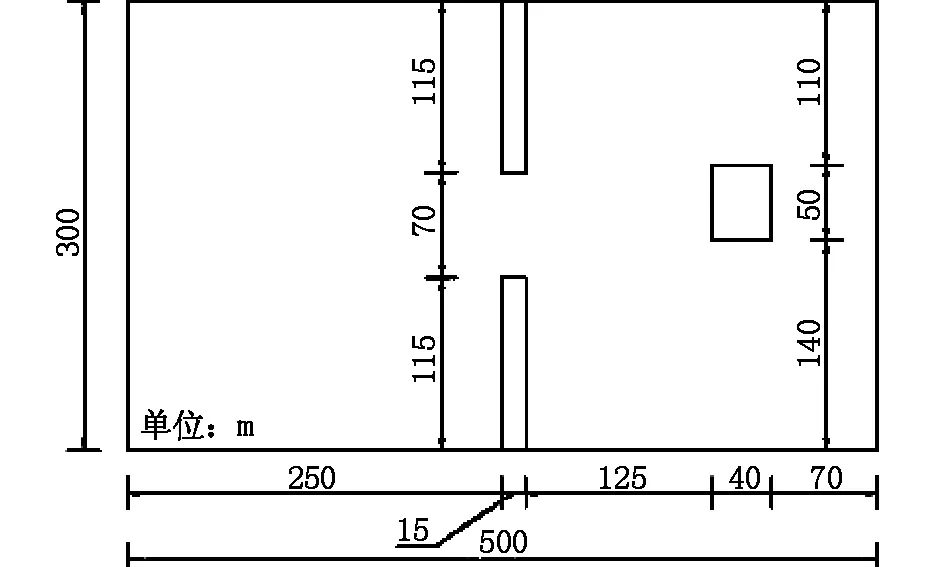
图1 算例模型平面尺寸

3 模型建立

本文采用某实际河道堤防简化建模，模型尺寸为700 m×160 m×10 m(长×宽×高)，模型包括尺寸为700 m×100 m(河底)×10 m(长×宽×高)的河道、河道两岸堤防与堤脚处等高的尺寸为700 m×50 m×10 m(长×宽×高)的平地；模拟河道坡降和糙率分别设为0.3‰和0.025，河道堤防高10 m，堤顶宽4 m，两侧边坡分别为1∶1.05、1∶0.85，设置决口处距离下游河道200 m[9]；河道堤防断面及Flow-3D模型三维图见图3。

河道模型网格划分为2 m×2 m×1 m，在决口50 m×50 m平面范围内进行网格局部加密，加密网格为1 m×1 m×1 m。模型初始条件为设置河道水位为5 m；物理边界条件：重力Z方向给定一个重力加速度，x、y方向不做设置；不同水头工况下模拟设置初始流量为800 m3/s，水位随工况变，不同流量工况下模拟设置初始水头6 m，流量随工况变；下游河道设为自由出流；模型顶部设置压力为一个标准大气压压力边界条件，模型底部和左右两侧皆设定为固壁边界。求解时间设为600 s，时间步长设为2 s。决口口门三维结构尺寸及平面尺寸见图4，图中x方向为河道水流方向(模型中坐标为470～500)，y方向为决口水流方向(模型中坐标为100～120)，选择图4中的A-A和B-B截面的水深和流速计算结果进行分析。

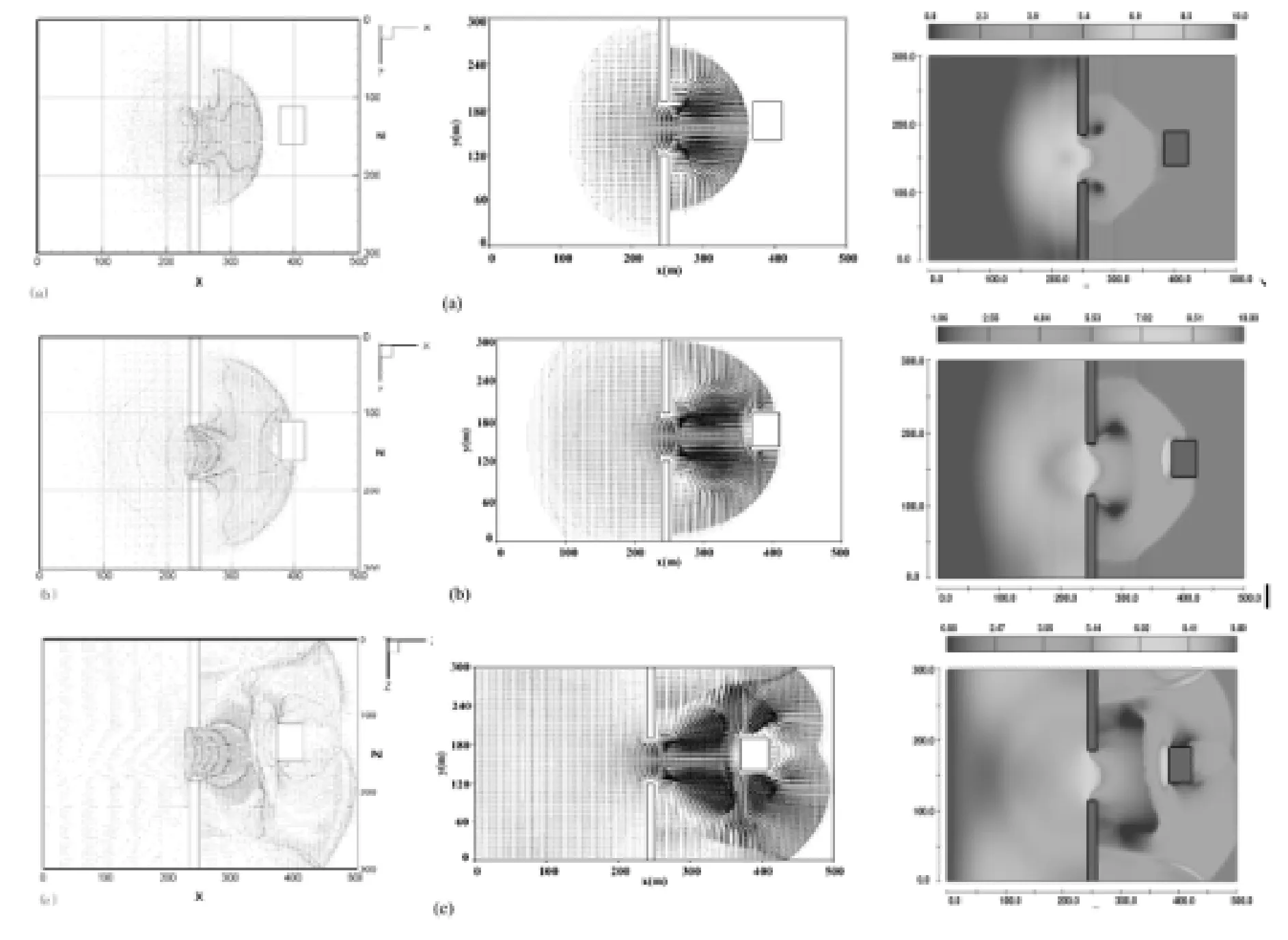
图2 FLUENT、Wang、FLOW-3D计算的速度场结果(时间分别为12 s、18 s、32 s)

图3 河道堤防断面及Flow-3D模型三维图

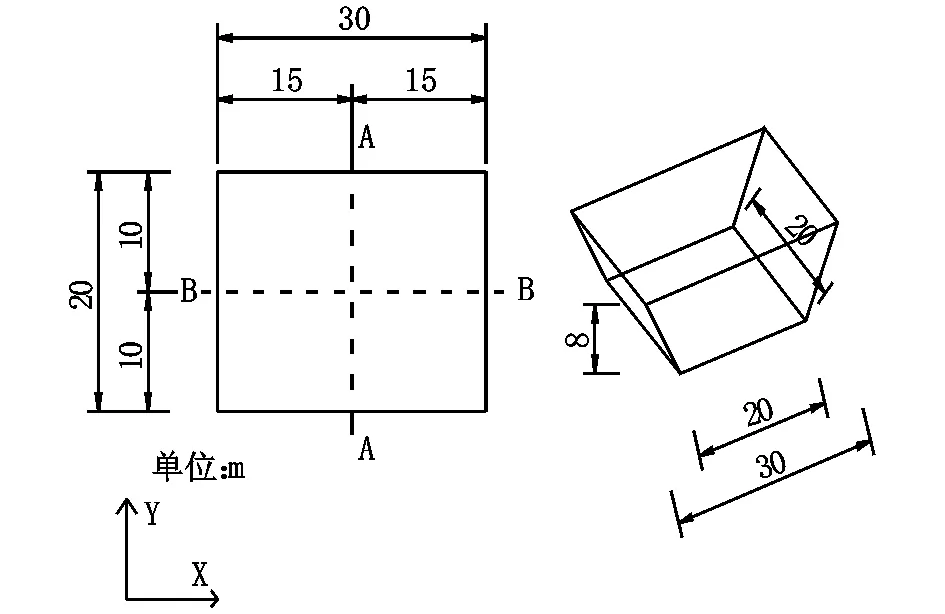
图4 模型决口口门平面尺寸及三维结构图

4 不同水头作用下堤防决口的水力学特性分析

本文分别对河道上游水头为6 m、7 m、8 m、9 m的条件下T形决口(图4)为例进行堤防决口水力学特性的数值模拟。表1为不同水头作用下决口处水流流态达到稳定所需的时间，由表可知，在给定河道初始水位为5 m、上游来水流量不变的条件下，决口水流模拟达到稳定的时间不会随上游水头的增大而发生改变。本文主要对不同水头作用下水流流态达到稳定后的决口处平面流速场分布规律及A、B各断面的水面线和流速水力数据进行分析。

表1 不同水头作用下数值模拟稳定时间

4.1 流速场分布

图5是不同水头作用下决口平面三维流速场。从图中可以看出，不同水头作用下的决口流速场分布几乎完全一致，水流在决口进口左右两侧产生侧向收缩，水流产生明显的纵向跌落；因模型设置决口出口为无任何阻挡物的平地，水流沿决口口门出口在重力势能作用下向四周扩散，故沿决口水流方向，流速逐渐增大；在垂直于水流方向上，因口门形状比较规整，在堤脚处产生了水跌，水流紊动剧烈，流速较大。从图中可以明显看到决口平面处的较大流速主要分布在决口进口上游左侧发生水跌处(图中红色部分)，决口进口右侧河道内水流流速几乎为0(图中蓝色部分)。在进行决口封堵时，当决口来水侧水流流速大，水流运动紊乱，应考虑在该侧进行裹头处理，从决口下游侧采用单边进占封堵，直至合龙。

图5 不同水头下T形决口三维流速场

4.2 A截面水面线和流速结果分析

图6和图7分别是不同水头作用下A-A断面的水面线和流速。从图中可以看到，不同水头作用下的水面线沿水流方向产生纵向跌落，水位沿水流方向距离堤脚处越远，水位越低，水位逐渐降低，水面线为正比降，四种水头下的水面线基本平行；水流沿水流方向距离堤脚处越远，流速越大。在106.5 m≤y≤116.5 m之间，各不同水头作用下流速分布是6 m水头<7 m水头<8 m水头<9 m水头；在y≤106.5 m、116.5 m≤y范围内，各不同水头作用下流速分布规律不明显，流速线有部分交叉，较大流速分布在决口下游出口边界处。随着作用水头的增加，决口中轴线A-A断面处的水位和流速随之加大。

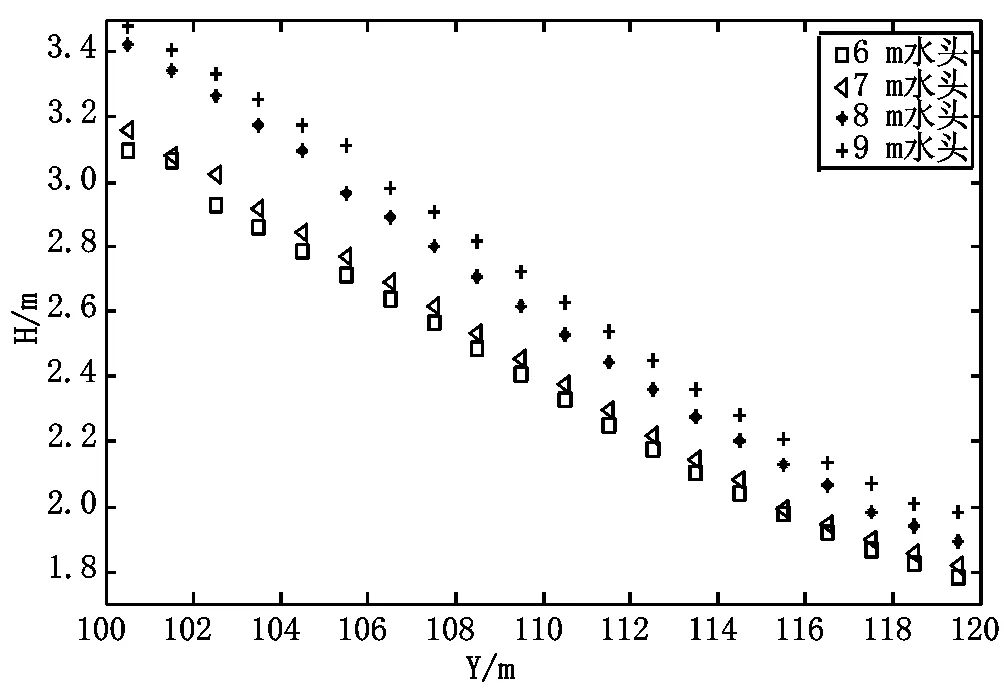
图6 不同水头下A-A断面水面线

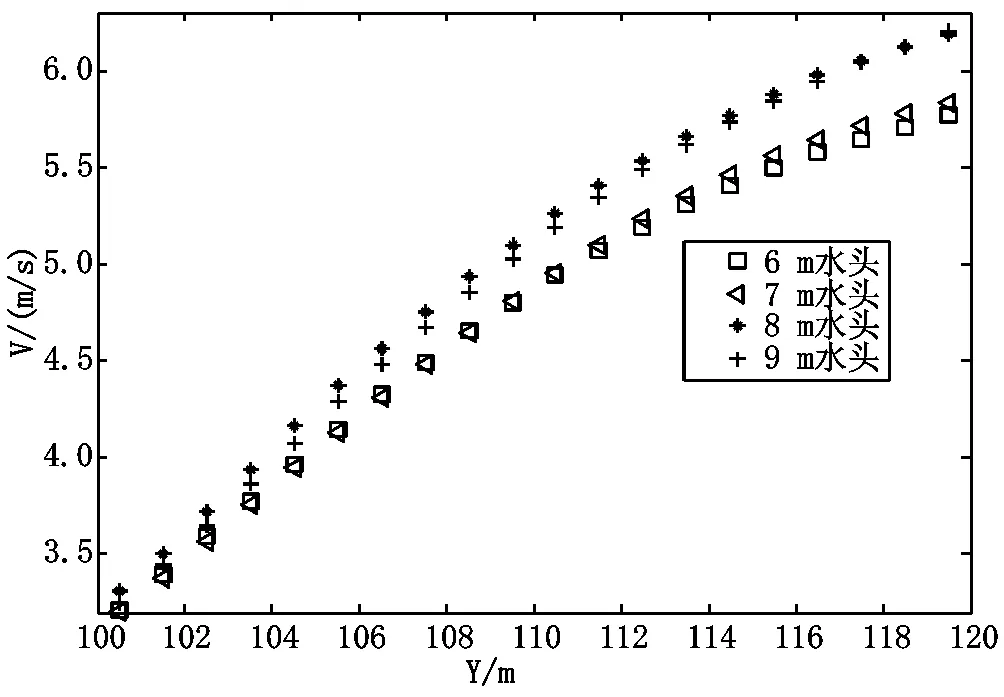
图7 不同水头下A-A断面流速

4.3 B截面水面线和流速结果分析

图8和图9分别是B-B断面的水面线和流速。B-B断面的水面线呈现左边峰值较低、右边峰值稍高的高拱形不对称分布，和流速分布正好相反，各不同水头作用下溃口的水面线、流速变化规律一致，且数值都比较接近，水面线互有一定交叉；从表2中和图8、9中可以看出，8 m水头作用下的B截面断面流速均稍大于9 m水头作用下的B截面断面流速，这是因为在上游流量一定的情况下，进入决口的流量相差不大，而T形决口随着决口处水面的增高其过水断面面积增大，在流量相差不大的情况下，过水面积增大，流速减小。从B-B断面最大水位和最大流速分布(表2：流速单位m/s，水深单位m)可以看出，决口较大的流速分布在决口进口上游侧，随着作用水头的增加，堤防中轴线B-B断面的水位和流速随之加大。

表2 不同水头下B-B断面最大水位和最大流速分布

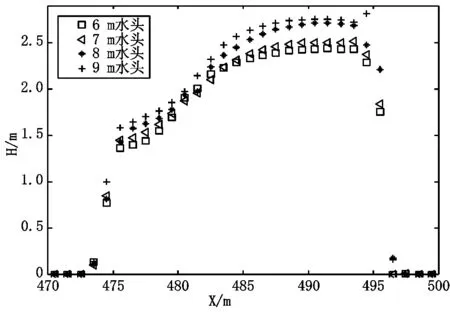
图8 不同水头下B-B断面水面线

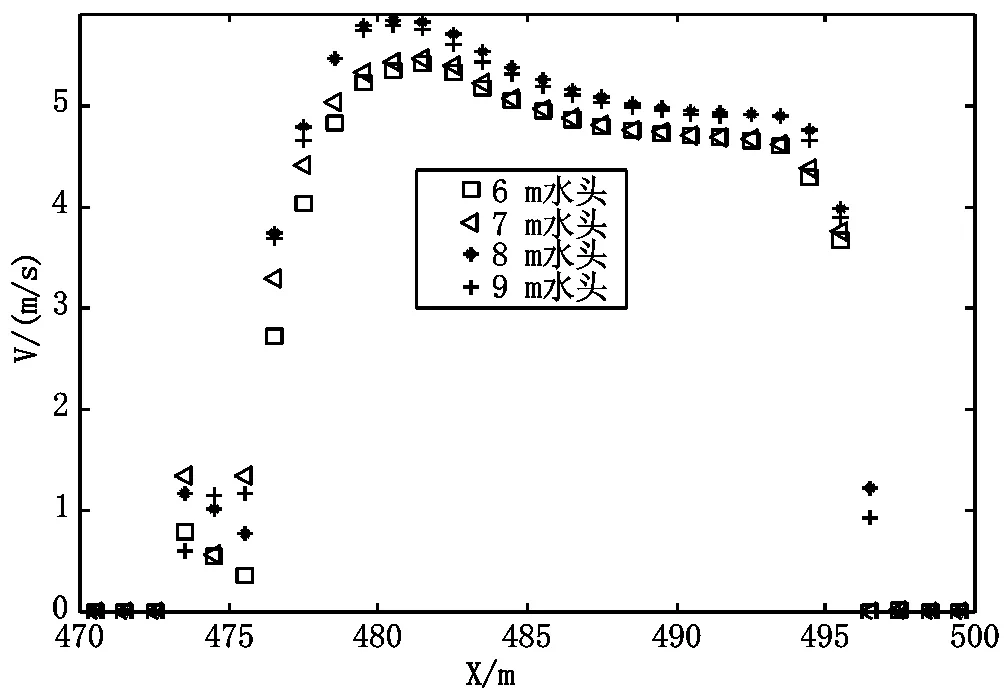
图9 不同水头下B-B断面流速

5 不同流量作用下堤防决口的水力学特性分析

河道上游不同流量条件对决口处的水力学特性参数也会产生不同的影响，本文分别对河道上游流量为400 m3/s、600 m3/s、800 m3/s、1 000 m3/s和1 500 m3/s的条件下进行堤防决口水力学特性的数值模拟。表3为不同流量下决口处水流流态达到稳定所需的时间。由表3可知，在给定河道初始水位为5 m、上游水头不变的条件下，决口水流模拟达到稳定的时间随上游来流量的增大而减小。因不同流量作用下水流流态达到稳定后的决口处平面流速场分布规律与不同水头作用下流速场分布规律比较类似，这里不再赘述，本节仅对A、B各断面(见图4)的水面线和流速水力数据进行分析。

表3 不同流量作用下数值模拟稳定时间

5.1 A截面水面线和流速结果分析

图10和图11是不同流量作用下A-A断面的水面线和平均流速。从该图可以看到，不同流量作用下的水面线沿水流方向产生纵向跌落，决口进口断面和出口断面水位相差较大，各不同流量作用下的水面线基本为线性线段，基本互相平行，决口处水深随上游来流量的增加而增大。各不同流量作用下决口处各断面的流速都是沿水流方向逐渐增大，断面上各点流速随距堤脚线距离越远基本成线性增长，流速变化规律相似，较大流速分布在决口下游出口边界处。

图10 不同流量下A-A断面水面线

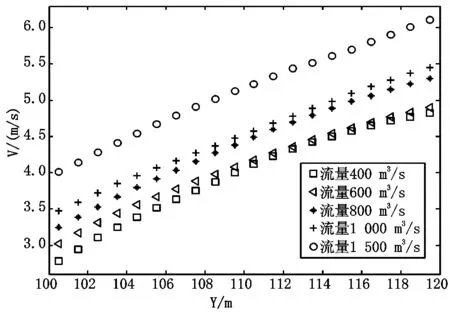
图11 不同流量下A-A断面流速

5.2 B截面水面线和流速结果分析

图12和图13是堤防中轴线断面B-B断面的水面线和平均流速。该断面的水面线呈中间高、两边低的高拱形，决口左侧水位都比较低，中轴线附近及偏口门右侧水位较高；流速呈左边峰值较高、右边峰值稍低的城门洞形不对称分布；各不同流量作用下溃口的水面线和平均流速变化规律一致。从B-B断面最大水位和最大流速分布(表4流速单位m/s，水深单位m)可以看出，决口较大的流速分布在决口进口上游侧，随着上游流量的增加，堤防中轴线断面处的水位和流速随之加大。在纵向上决口水位随距堤脚线距离越远而减小，流速在横向上从左到右先增大后减小，决口左侧边界附近流速较大，中间部分流速较小。

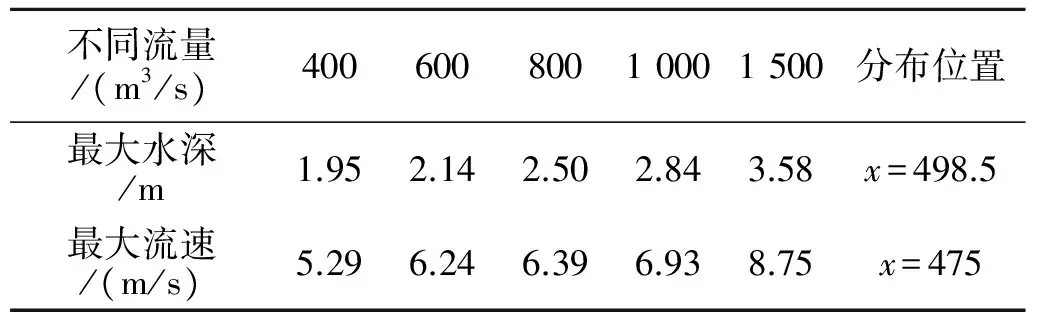
表4 不同流量下B-B断面最大水位和最大流速分布

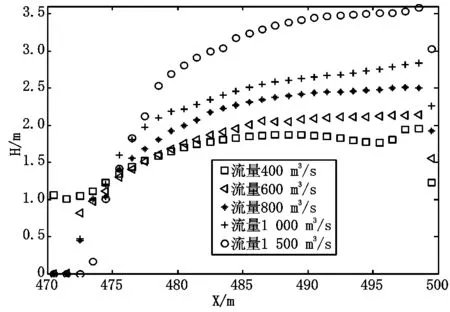
图12 不同流量下B-B断面水面线

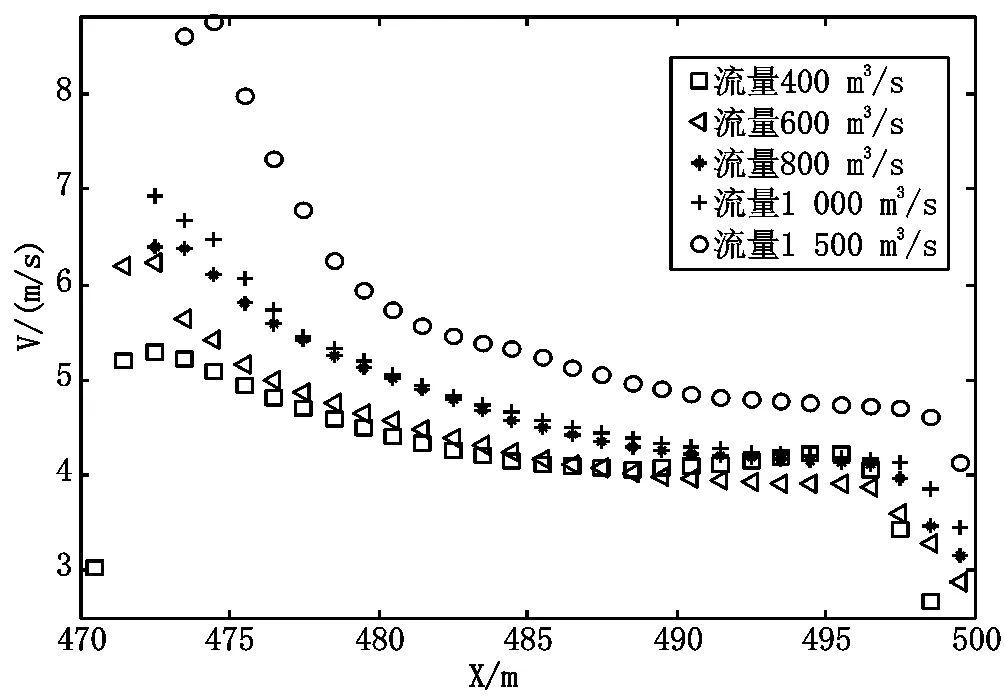
图13 不同流量下B-B断面流速

6 结 论

本文采用Flow-3D对某实际河道的堤防进行决口三维模拟，主要分析了在口门形状及大小一定的条件下不同水头、不同流量作用下的决口处水深和流速的分布特征，得到如下结论：(1)水位：各不同水头、不同流量作用下的水位在横向上是溃口左右两侧边界处低、中间高，水流溃口水面线在横向上呈两边低、中间高的拱形。(2)流速：不同水头、不同流量作用下，溃口流速分布在横向上呈两边低、中间高的拱形；决口较大的流速主要分布在决口进口上游左侧发生水跌处。因此，在进行决口封堵时，应注意预先做好决口上游侧的裹头处理，防止在封堵的过程中因流速过大导致溃口口门扩宽；在选取封堵材料时，也可根据溃口处流速分布来选择相应的封堵料粒径。本文基于Flow-3D建立的堤防决口三维模型和模拟方法均可为制定有效的决口封堵方案提供科学依据和技术参考。

[1] 孙芦忠，赵建均，严建国，等.堤防决口的水力学试验研究[J].人民长江，2003，34(11)：41～42.

[2] 李火坤，邓冰梅，曾秀娟，等.堤防决口水流水力学特性的三维数值模拟[J].水利水运工程学报，2016(6)：29～36.

[3] 李火坤，曾智超，邓冰梅，等.堤防决口封堵的水力学特性研究[J].水利水运工程学报，2017(3)：8～15.

[4] 罗娜，刘成林，陈宇豪.堤防决口下游泥沙冲刷的三维数值模拟分析[J].南昌大学学报(工科版)，2016，38(4)：360～365.

[5] 王月华，包中进，王斌.基于FLOW-3D软件的消能池三维水流数值模拟[J].武汉大学学报(工科版)，2012，45(4)：454～457.

[6] 包中进，王月华.基于FLOW-3D软件的溢洪道三维水流数值模拟[J].浙江水利科技，2012(2)：5～9.

[7] 曾秀娟.堤防决口封堵水力学数值模型研究[D].南昌大学，2015.

[8] 林长强.基于FLUENT的土石坝逐渐溃坝水流模拟[D].华中科技大学，2011.

[9] J.S.Wang，H.G.Ni，Y.S.He.Finite-Difference TVD Scheme for Computation of Dam-Break Problems.Journal of Hydraulic Engineering，2000，126(4)：253～262.