泰勒公式在《数学分析》解题提高中的应用研究

王照生

(赣州师范高等专科学校, 江西 赣州 341000)

一、引言

泰勒公式是《数学分析》微积分中非常重要的公式，是利用函数在已知点的性质求解函数值的有利解析工具，在解决函数极限，近似计算，积分运算，级数敛散性判断等问题上有着广泛应用。《数学分析》教材对泰勒公式在解题中的应用涉及偏少，缺乏涉及各方面解题技巧的系统性阐述；另外泰勒公式的表达式较长，因此学生在解题中不太喜欢使用它，学生在学习中缺乏应用泰勒公式解题的意识。事实上，在数学分析解题中灵活运用泰勒公式，会给我们带来极大的便利。

二、泰勒公式

泰勒公式常用的有两种形式的余项——拉格朗日余项和皮亚诺余项．为应 用方便，我们先把公式叙述如下：

定理1[1]（带拉格朗日型余项的泰勒公式）设函数f(x)在含有x0的某个区间（a，b）内具有直到n+1阶的导数，则对任意 x，x∈(a，b)，有

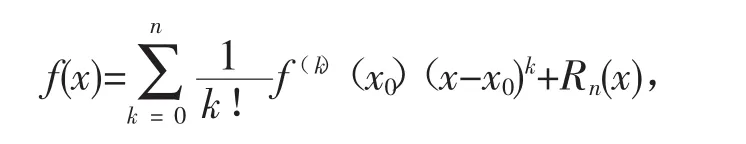
定理2[1]（带皮亚诺型余项的泰勒公式）设函数f(x)在0点的某个邻域内有定义，并在x0点有n阶导数（n≥1），则在x0点附近有下列展开式：

其中 Rn(x)=o(x-x0)n，x→x0。

当x0=0时，泰勒公式称为麦克劳林公式．带拉格朗日余项的泰勒公式在整个区间（a，b）内都成立，所以也叫做整体泰勒公式。而带皮亚诺余项的泰勒公式只在x0点附近成立，所以也叫做局部泰勒公式。

三、活用泰勒公式巧解题举例

（一）求极限

（二）无穷小量阶的比较

例2设函数f（x）=x+aln（1+x）+bxsinx，g（x）=kx3在x→0时为等价无穷小，求常数a，b，k的取值。

由于当x→0时，f（x）：g（x），则结合等价无穷小定理，有

（三）求函数在给定点x0处的高阶导数

例3求函数f（x）=x2，2x在x=0处的阶导数f（n）（0）。

等式右端xn的系数为，于是

注 本题的求解体现出泰勒公式的优越性。

（四）在证明不等式上的应用

泰勒公式在证明不等式时，条件约束低，只要函数在二阶或二阶以上可导，即可使用泰勒公式。

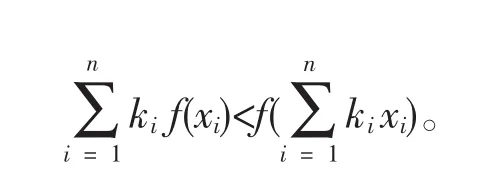
证 f(x)在[a,b]上二阶可导，从而f(x)用泰勒公式展开得到二阶形式

选择 x=xi从而上式为

将ki乘上式两端，然后n个不等式相加，得出

本例提示：在解题中，可以具体问题具体分析，选取泰勒公式的展开式。

（五）泰勒公式在近似计算上的应用

例5[2]求方程的近似解，精确到 0．001。

即当即为满足题设条件的解。

（六）在级数收敛性的判定

由题设可知f″(x)在包含原点的某个闭区间[-δ,δ](δ〉0) 上连续，则存在 M〉0，当 x∈[-δ,δ] 时，有则收敛，由比较判别法知收敛，从而级数绝对收敛

四、小结

解题中发现，用泰勒公式来解题往往方法简单，因为泰勒公式本质上可以将一些复杂的函数近似地表示为多项式函数，多项式函数是数学中最简单的一类函数，对其研究自然更简单，可以大大提高解题效率。

[1]同济大学数学系．高等数学（上册）[M]．北京：高等教育出版社，2014．

[2]陈兆斗，郑连存，等．大学生数学竞赛习题精讲[M]．北京：清华大学出版社，2010．