基于DCS的电力节能优化控制系统的设计与实现
付 ,廖 臣,汪 浩
(贵州电网有限责任公司信息中心,贵阳 550000)
0 引言
随着社会飞速发展,人们对生活质量的要求越来越高,这样一来,电力资源就会在人们的生活中扮演不可替代的角色。这样给电力系统的发展提出更高要求,带来更大的挑战。随着国家电力系统发展的越来越庞大,系统运行机制和模式也更加的复杂多变[12-15],一旦出现问题,远非传统方法能够有效解决。在电力系统中,用传统算法设计系统居于主流,不过,实际的用电情况变化非常复杂,如果系统不进行优化设计,则无法满足需求,这样一来就要浪费大量的电力能源。而电力系统的实时运行会增加非必要能源的消耗,这样,越来越多的科研工作者就投身于节能优化系统的开发当中去了[1]。
另一方面,DCS(Distributed Control System)集散控制系统,又叫“分布式控制系统”。它综合了通信、显示和控制等多方面的技术,而又能组成多级计算机系统以实现分散控制、集中操作、分级管理、配置灵活等优势而在工业控制领域取得了相当广泛的应用,特别是应用在电力系统的企业生产中。目前,在电力系统中,不管是调度还是管理都急迫的需要强大的综合管理和优化控制的功能。这些都要求电力系统在运行过程中要有安全可靠、实时有效和灵活组态等特点,从目前这些要求来看,DCS能够满足以上应用的要求[2]。
本文运用DCS技术,建立了电力系统节能控制软件模型,设计了电路转换控制软件,同时提出了一种多重自适应的粒子群优化算法,结合不同算法下的仿真结果,设计与实现了基于DCS的电力节能优化控制系统,有效地优化了电力能耗。
1 电力节能控制系统设计
1.1 DCS管理控制原理
DCS的结构主要分为四层,即管理层、系统控制层、现场控制层和设备层。
其结构如图1所示。其中,管理层的设备主要包含操作员站还有工程师站、与分散的控制系统进行信息交流的人机接口及监测整个系统中各部分的运行情况。系统控制层是来负责接收安放在现场的电力设备发送回来的电信号,按照早就已经安排好的控制策略算出控制量并返回给现场设备。现场设备层安排的位置在被控生产过程的周围地带,该层作用是将生产过程中采集到的各种物理信号转化为电信号,以便传输[3]。

图1 DCS系统结构
在实际电力系统中,DCS中包含了大量的传感器,各种转换器,它们能够将设备层中的电力设备的运行状态、使用的电量和一些非电量信号信息及时收集上传到服务器,然后将信号上传至管理层中的控制计算机上,最后按照之前就人为设定好的算法模型进行判断、运算,得出结果后发送命令给被控的设备[4]。
1.2 节能软件模型的建立
为了能够使工作人员更方便地了解能源消耗情况,需要对能源消耗进行计算统计,这样可以方便节能软件模型的建立。通常利用以下公式对电力系统处于运行和不运行两种状态下的能源消耗计算:
(1)
上面公式是运行状态时计算能源消耗的公式,是电力运行过程中的电容,是电压大小,a是电流变换的频率,t则是系统的运行持续时间[5]。需要对公式中的数据参数进行逐条记录,这样一来,可以转化为一组对应的元件电阻集合。当电压为Uk时,系统运行消耗的能源量的计算公式为:
(2)
其中:tj是电力系统第j次连续运行的时长,Uj是第j次运行时的电压大小,aj为电力元件电流的变换频率。现实情况中,系统实际运行过程中还会有部分与电力系统运行无关的参量存在,这些参量可计算电力系统的非必要能源消耗,也就是电力系统在停止运行状态下消耗的能量。公式如下:
Ru=Xd·Ku+|Xd|(kl+kd)
(3)
其中:Xd表示电力系统在停止运行状态下的电压,Ku表示电流。上述所提公式能够计算出一般情况下的电力系统的能源消耗,为计算机软件仿真设计系统控制能源消耗提供参考依据[11]。
另一方面,电力系统能源消耗的另一个重要因素是电路的转换过程。在转换过程中一般会有大量的电力能源资源消耗,因此在节能软件设计过程中不能忽略电路转换过程的能源消耗。电路状态之间的转换过程可分为两种,通常可以用二进制(0和1两种状态)清晰直观地表现出来。在设定的时间段内,根据如下公式可计算出系统中电流状态改变的能源消耗的变化过程:
(4)
上面的公式可以用来实时地监测电路转换过程中的能源消耗。同时工人也可以通过所记录下的参数来计算出电力系统的最高效率,以便算出转化过程中的能源消耗。
1.3 节能控制系总体设计方案
本文综合考虑电力系统实际耗能情况,在DCS控制系统的基础上提出一种基于DCS的电力节能控制系统的模型,该模型由控制器,监测设备,电力设备三块组成。如图2所示。监测设备负责将电力设备的耗能情况汇总反馈给控制器,控制器通过合理算法计算出科学的运行方式以达到减少非必要能源的消耗,并实时控制着电力设备的运行。由于DCS系统能够实现实时自动化管理,所以该系统亦可节约一部分人力资源。
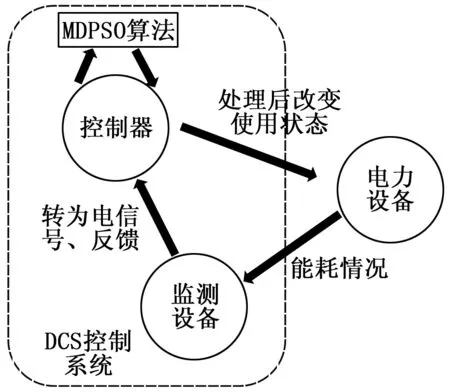
图2 节能控制系统框架图
DCS控制系统使用FOXBOROI/A系统,控制器使用FCP270。在DCS软件设计中,为了实现PID控制功能,使用PIAD模块[16]。为了使控制过程稳定精确,分别设置各参数如下:控制器设为自动,置位FBTUNE.STNREQ,比例带PBAND=290.48分钟,积分时间INT=1.22分钟,微分时间DERIV=0,低通滤波器增益参数KD=0.1,设定值超前滞后系数SPLLAG=0.81。
2 改进的粒子群优化算法
粒子群算法(Particle Swarm Optimization,PSO)是一种群智能优化算法,它简单并且容易实现、能够实现并行搜索而且计算效率高,适用于解决复杂的最优化问题,该算法能以比较大概率寻找出全局最优解。近年来,许多领域中的科研工作运用了粒子群算法,显示了该算法的广阔的应用前景。
2.1 一般电力系统调度算法
当前较为流行的电力系统节能调度算法使用的自适应粒子群算法[12],不使用复杂学习策略,考虑为了减少时间复杂度,使用进化代数来修改惯性权重和学习因子[6]。
一般的电力系统需要在调度中找到最优最节能的调度节点,找最优点是靠算法需要有全局搜索的功能,一旦粒子的目标函数改变,调度点的惯性权重也随之变化。整个过程大体如下[7]:
算法关键点在于权重因子的变化方式,增加惯性权重的条件是电力系统中调度的节点中的各个调度目标值向相同的最优值靠拢或者有这个趋势,相反,如果各个电力节点的目标不趋于一致,那么就要根据进化代数的情况来改变惯性权重的大小了,这样做是要使得该节点向全局最优解靠。表达式如下:
(5)
就目前普遍的电力系统调度过程中,调度学习因子取常数,工程上一般取值为2。另外,一般有两种方法确定自适应学习因子,而在实际是同步变化的方法[8],如下:
(6)
在系统优化过程中,公式(6)中两个调度因子随着进化代数变化而改变,粒子在一开始时学习自己的能力比较强而学习社会同类的能力非常弱,这样就会使得整个算法体系的全局搜索能力强。而在运行过程的后期,进一步强化了全局搜索能力[9-10]。
如果我们尝试将上述电力系统节能调度方法,惯性权重因子自适应的方法和同步自适应学习的方法有机结合起来,并考虑在传统的电力系统节能调度过程基础上的一些其他因素,就能够得到一种从未有过的电力调度节点最好的位置的迭代公式,如下:
vi,j(t+1)=wa*vi,j(t)+Ca*r1*
[pi,j-xi,j(t)]+Ca*r2*[pg,j-xi,j(t) ]
(7)
(8)
其中:vi,j是粒子的速度,wa是惯性权重,xi,j(t)是粒子当前位置,pi,j(t)是粒子当前最优位置,pg,j(t)是粒子的全局最优位置。不过,该方法没充分考虑电力非线性时变,所以节能效果不是很理想。
2.2 改进多重自适应的粒子群优化算法(MDPSO)
传统的基于PSO的节能控制方法的目的是找到整个系统的发电成本最小的那个状态,这样依赖就存在一些难以解决的问题,例如线路阻抗小等等的一些特殊情况下,弱耦合性会出现在输电线路的传输能量的功率和所需要花费的成本之间,把功率与成本关联计算,控制过程不收敛,结果不最优[11-12]。本文提出一种多重自适应粒子群优化算法(MAPSO)。
首先,在给定的搜索空间内随机地生成数量较多的粒子,接着,就是粒子位置与速度两个参量的更新方法。分别是根据计算得到的当前的最优位置和最优速度来进行相应的调整,过程中惯性权重w和学习因子c也根据情况相应的调整,这样做是为了调度的全局最优值成为所有粒子的靠拢点[13-14]。如果尝试将该算法用于电力节能优化系统的设计中,就能很好地对电力能耗进行优化控制,而且实用性高。
具体步骤如下:
步骤1:初始化,确定给定的搜索空间E,从E中选取size个粒子{ei1,…,eisize}产生随机粒子种群P(t)={Pj|j=1,2,…,size}和速度vj(t)。
步骤2:确定好目标函数f(pj)和所有产生粒子{eij},算出目标函数取值。
步骤3:算出来全局最优值vgbest(t)=maxpj∈P(t)f(pj(t))。
步骤4:根据进化代数,按照公式(7)和公式(8)更新惯性权重和学习因子。
步骤5:根据如下公式,改变粒子的位置和速度。
vj(t+1)=w·f(pj)+c1·r1·f(pbestj)+c2·r2·
f(gbest),j=1,2,…size
步骤6:根据按照前面步骤更新之后的粒子,计算新的目标函数值fnew(pj)。
步骤7:判断新的目标函数值fnew(pj)是否小于全局最优值vgbest。
步骤8:如果目标函数值大,全局最优值保持; 若否,用目标函数值换之。
步骤9:判断是否满足最大进化代数,不满足转步4;满足转下一步。
步骤10:输出全局最优值和全局最优变量取值。
3 系统集成和测试结果分析
3.1 基于DCS的节能优化系统实现
本文在DCS控制系统和MDPSO算法的基础上提出一种新的电力节能控制系统的模型,该模型由控制器,监测设备(包含一些传感器探测器和转换器),电力设备三块组成。并将文章第2部分所提算法有机地运用于控制器中。系统运行过程如下:一开始电力设备照常运行,监测设备负责将电力设备的耗能情况实时地汇总反馈给控制器,控制器将不断接收到的数据通过MDPSO算法,按照上一章设计的算法迭代步骤进行计算,每一轮都找出一种使得系统耗能最少的系统输出功率,如此不断搜索系统运行最优调度节点,找出一种使得整个系统输出功率最少的运行方式,并把产生的结果转变为控制命令发送给电力设备,实时控制电力设备的运行,经过一段时间的循环往复、不断调整,使得整个系统的耗能逐渐趋向于最低耗能状态,每个电力设备的非必要能耗大大减少,从而降低了整个系统的电力能源消耗。而整个监控体系都是由DCS来完成,这样减少一部分人力资源的消耗[15]。整个系统是在虚拟DCS环境中运行。
3.2 算法性能对比测试
判断多重适应粒子群算法的准确度要用到Benchmark函数。本文用5个函数,将基本PSO,自适应权重的PSO和多重自适应学习因子的PSO进行对比。
所选取的5个测试函数的搜索空间范围是[-200,200],为了能够简化测试复杂度,就要简化搜索的过程,我们所选搜索变量的维度为5。并与其他算法对比。结果如表1所示。
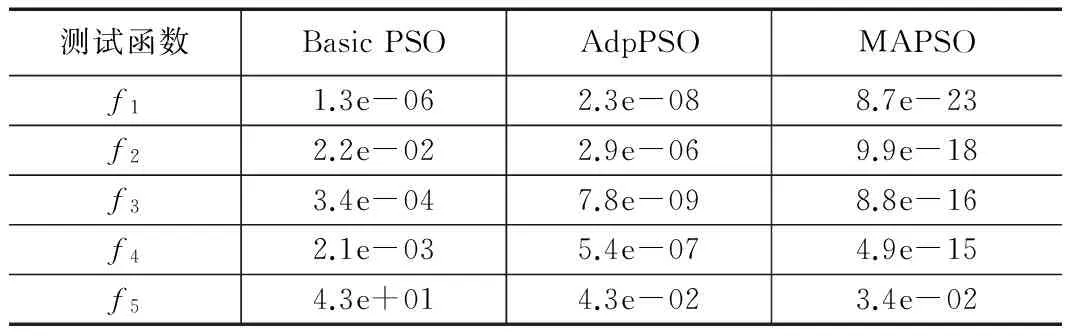
表1 算法对比测试结果
对3种算法各运行150次,取平均值。从表1的结果可以看出多重自适应的粒子群算法(MAPSO)的准确率比和自适应权重的粒子群算法(AdpPSO)都高。可见MAPSO的精度和性能都很好。
3.3 系统节能效果测试仿真
从上一小节的测试结果来看,MAPSO具有搜索精度高的优点,这就使得MAPSO可以应用于电力系统最优计算问题。把MAPSO算法应用于我们设计的基于DCS的电力节能优化系统中,使用该算法来控制电力设备的状态以达到减少非必要能源消耗的目的,用我们设计的电力节能控制系统和使用传统算法的一般电力控制系统对比,节能控制效果如图3和图4所示。我们使用电力系统节能参数来衡量节能系统节能效果,使用电力控制超调量来衡量系统控制效果。
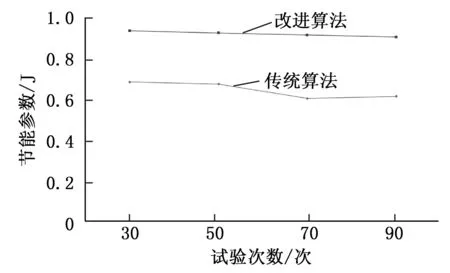
图3 电力系统节能参数对比

图4 电力系统控制效果对比
进一步分析可知,本文所提的基于DCS的电力节能优化控制系统使用所提算法的节能效果显著,而且该系统超调量波动比一般系统小,可见系统的响应速度快,控制效果好,更加稳定可靠。综合考虑把权重自适应机制和学习因子自适应机制有机结合起来的智能粒子群算法,这样做的好处是在运行过程中,惯性权重可以根据进化代数改变,而且学习因子能够一起也改变,这就使得整个系统算法进一步加强了它的全局搜索能力和收敛速度。仿真实验函数比现实问题更复杂,理论性也强。而现实优化问题比实验简单,因此,一个算法在测试实验上的表现非常理想,那么完全可以说明该算法完全可以应用于实际工程。当然,MAPSO有缺点,后期收敛速度会逐渐回落,增加时间成本。因此,考虑 MAPSO运用到实际工程上时,仍然需要进一步改进。
4 结束语
本文提出了基于DCS的电力节能优化控制系统,系统采用了一种多重自适应的粒子群优化算法。该系统结合了DCS良好的控制技术和多重自适应粒子群算法收敛速度快、搜索精确度高的特点。从数值仿真结果可以看出,所提系统和算法在电力节能方面有非常好的潜力。如果能根据实际情况进一步研究将该系统应用于工程当中去,可以预见能效地节约电力能耗,且能够节约一部分人力资源。
[1] 王 磊. 论电力系统数字仿真技术的现状与发展[J]. 企业导报, 2011(16):296.
[2] 刘 哲. DCS在火电厂中的应用分析[J]. 黑龙江科技信息,2012(3):14.
[3] 刘一福. DCS在火电厂应用中的普遍问题及分析[A]. 2004电站自动化信息化学术技术交流会议论文集[C].中国动力工程学会自动控制专委会、哈尔滨工业大学、重庆大学、华北电力大学,2004:4.
[4] 田 芳,黄彦浩,石东宇,等. 电力系统仿真分析技术的发展趋势[J]. 中国电机工程学报,2014(13):2151-2162.
[5] 冯冰玥,陈春新. 企业配电网电能计量装置及管理节能软件设计[J]. 硅谷,2014(22):12.
[6] 郭思源,李振文,洪 权,等. 基于自适应权重粒子群算法的PSS4B-W参数优化研究[J]. 湖南电力, 2017(01):14-17+23.
[7] 任子晖,王 坚. 一种动态改变惯性权重的自适应粒子群算法[J]. 计算机科学, 2009 (02): 227-229.
[8] 薛禹胜,罗运虎,李碧君,等. 关于可中断负荷参与系统备用的述评[J].电力系统自动化, 2007, 31(10):1-6.
[9] 张少华,刘 刚,李渝曾. 考虑提前通知的可中断负荷管理模型[J]. 电力系统及其自动化学报, 2008, 20(4): 63-66.
[10] 张长胜,孙吉贵,欧阳丹彤. 一种自适应离散粒子群算法及其应用研究[J]. 电子学报, 2009, 37(2): 299-304.
[11] 谢 晶. 电力系统节能优化控制过程仿真分析[J]. 计算机仿真,2014(8):110-113.
[12] 陈铸华,李 晓. 电力系统故障诊断的多智能体粒子群优化算法[J]. 计算机测量与控制, 2010,18(8):1753-1755,1758.
[13] 周利军,刘学军. 电力虚拟仪器数据采集电路设计与分析[J]. 计算机测量与控制,2003(9):707-709,715.
[14] 张 丹,佘 维. 基于Petri网的电力系统监控数据多点校核方法[J]. 计算机测量与控制,2016,24(4):101-104.
[15] 印 姗,王 远,张 成. 基于嵌入式操作系统的无线电力监测系统设计[J]. 计算机测量与控制,2017,25(3):22-23,28.
[16] 钟 洋. I/A DCS系统的PID参数优化整定[J]. 仪器仪表用户,2013,20(06):45-47.

