The Interface Stress Field in the Elastic System Consisting of the Hollow Cylinder and Surrounding Elastic Medium Under 3D Non-Axisymmetric Forced Vibration

Surkay D. Akbarov and Mahir A. Mehdiyev

1 Introduction

In many cases the system consisting of the cylinder and surrounding elastic medium is used as a model for studying static, stability loss and dynamic problems related to the pipelines,tunnels, subway lining, mine works and other type underground structures. Therefore, the theoretical study on the dynamics of the bi-material elastic system consisting of the hollow cylinder and surrounding elastic medium to which the investigations carried out in the present paper regard also, has a great significance not only in the theoretical sense but also in the practical sense.

However up to now the related investigations are made mainly for the plane-layered systems whose beginning is the investigations carried out in the paper by Lamb [Lamb(1904)]. The review of these investigations is made in the monograph by Akbarov[Akbarov (2015)] and other ones listed therein. Here we consider a brief review some of them which are made approximately in last ten years and begin this review with the papers by Akbarov [Akbarov (2006a, 2006b)] in which the axisymmetric time-harmonic Lamb’s problem is investigated for the finite-pre-strained highly elastic bi-material elastic system consisting of a covering layer and half-space [Akbarov (2006a)] and for the bi-material elastic system consisting of bi-layered slab and of a rigid foundation [Akbarov (2006b)].In these papers it is assumed that the materials of the constituents are incompressible ones.In the paper by Akbarov [Akbarov (2013)] the foregoing problem related to the system“covering layer+half-space” is studied for the case where materials of the constituents are compressible ones. Moreover, in the paper by Akbarov et al. [Akbarov and Guler (2005)]the Lamb’s problem is investigated for a “pre-stretched covering layer+ half-space” system under a time-harmonic strip-loading.

In all the reviewed above works it is assumed that the materials of the constituents are isotropic. The case where the materials of the system consisting of the pre-stretched covering layer and pre-stretched half-plane are orthotropic, is considered in the paper by Akbarov and Ilhan [Akbarov and Ilhan (2010)]. The same problem for the case where the materials of the system are piezoelectric ones is considered in the paper by Akbarov and Ilhan [Akbarov and Ilhan (2013)]. Note that the main attention in these works is focused on the frequency response of stresses acting on the interface plane between the covering layer and half-space.

However, the investigations carried out up to now and related to the forced vibration of the system consisting of a hollow cylinder and surrounding elastic medium is not so much as those made for the plane layered systems. The investigations regarding to the dynamics of this system relate mainly to the moving load and wave propagation problems. Now we attempt to review briefly these investigations and begin this review with the paper by Parnes [Parnes (1969)] in which a dynamics of a ring load moving with constant velocity in the axial direction acting in the interior of a circular bore in an infinite homogeneous elastic medium, is investigated. It is assumed that the velocity of the moving load is greater than the shear wave velocity in the medium and all the theoretical investigations are made for the 3D case, however the numerical results on the stress and displacement distributions are presented for the corresponding 2D, i.e. for the axisymmetric case. In the paper by Parnes [Parnes (1980)] the aforementioned investigations are made for the case where in the interior of the cylindrical cavity a torsional moving load acts.

The investigation on the moving load problem for the system consisting of a thin cylindrical shell and surrounding transversally isotropic medium is examined in the paper by Pozhuev [Pozhuev (1980)]. The paper Abdulkadirov [Abdulkadirov (1981)] also studies the critical velocity of the moving ring load acting on the system “hollow cylinder+surrounded elastic medium”. The study of the dynamics of the ring moving load acting in the interior of the hollow cylinder which imperfectly bounded to the surrounded fluid-saturated permeable formation, is made in the work Hasheminejad and Komeili[Hasheminejad and Komeili (2009)]. Similar investigations were also made in recent years in the papers by Hussei et al. [Hussei, François, Schevenels et al. (2014)], Yuan et al. [Yuan,Bostrom and Cai (2017)] and others listed therein. Moreover, in recent years, numerical methods based on various type finite elements are developed and applied for investigations of the dynamics and statics of the elastic and piezoelectric systems (see, for instance the papers by Fan et al. [Fan, Zhang, Dong et al. (2015); Bui, Zhang, Hirose et al. (2016);Babuscu Yesil (2017); Wei, Chen, Chen et al. (2016)] and others listed therein).

It follows from the foregoing review that the investigations related to the forced vibration of these system are absent almost completely.

It should be noted that the first attempt on the study of the axisymmetric forced vibration of the “hollow cylinder+surrounding elastic medium” under perfect and imperfect contact between the constituents is made in the paper by Akbarov et al. [Akbarov and Mehdiyev(2017)]. It is assumed that on the inner free face of the cylinder a point-located axisymmetric time-harmonic force, with respect to the cylinder’s axis and which is uniformly distributed in the circumferential direction, acts.

However, in many real cases a non-axisymmetric dynamic loading cases in the interior of the hollow cylinder surrounded with elastic medium take place. Consequently, for controlling and describing of the stress-strain state in the engineering systems modelled as“hollow cylinder+surrounding medium” require the study of the corresponding nonaxisymmetric forced vibration problems to which the present paper relates.

2 Formulation of the problem

Consider the “hollow cylinder+surrounding infinite elastic medium” system and assume that the thickness of the cylinder is and the external radius of the cross section of this cylinder is The sketch of thesystem is shown in Fig. 1, according to which, the cylindrical system of coordinate is associated with the axis of the cylinder. Assume that in the interior of the cylinder the point located with respect to the cylinder axis and non-uniformly distributed in the circumferential direction time-harmonic normal forces act.Within these frameworks we investigate the non-axisymmetric strain-stress state in the system under consideration.

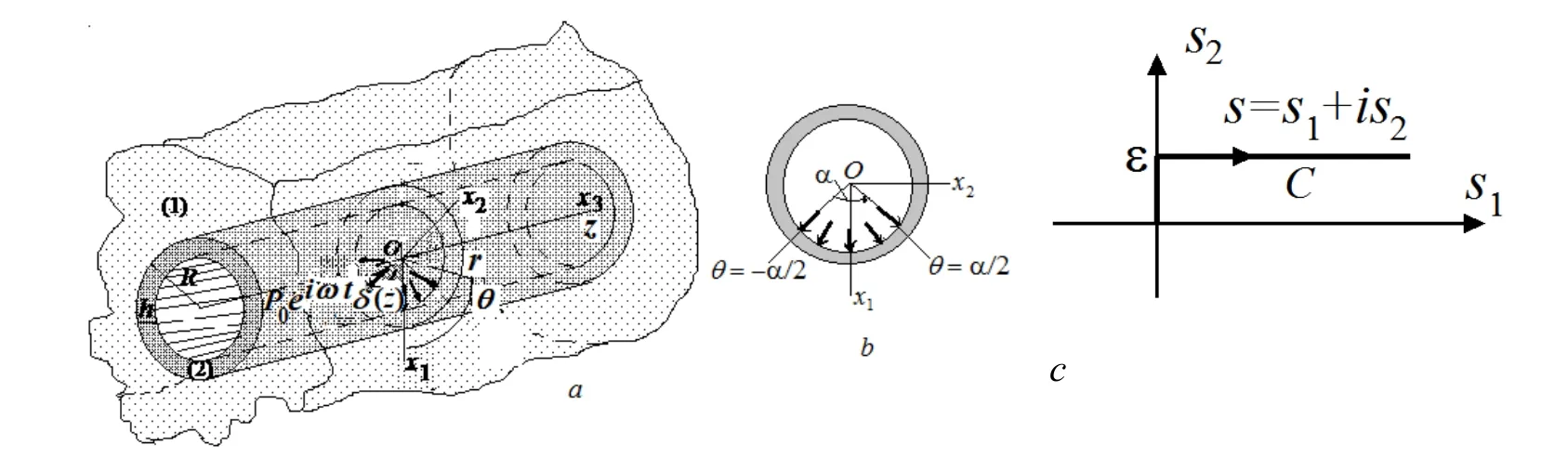
Figure 1: The sketch of the considered system (a) and the sketch of the distribution of the non-axisymmetric normal forces (b); the sketch of the Sommerfeld contour (c)

Below, we denote the values related to the hollow cylinder and to the surrounding elastic medium with the upper indices (2) and (1) respectively.

Assume that the materials of the cylinder and surrounding elastic medium are homogeneous and isotropic, and write the field equations, relations and boundary and contact conditions in the selected cylindrical system of coordinates.

Equations of motion:

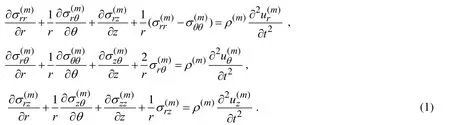
Elasticity relations:

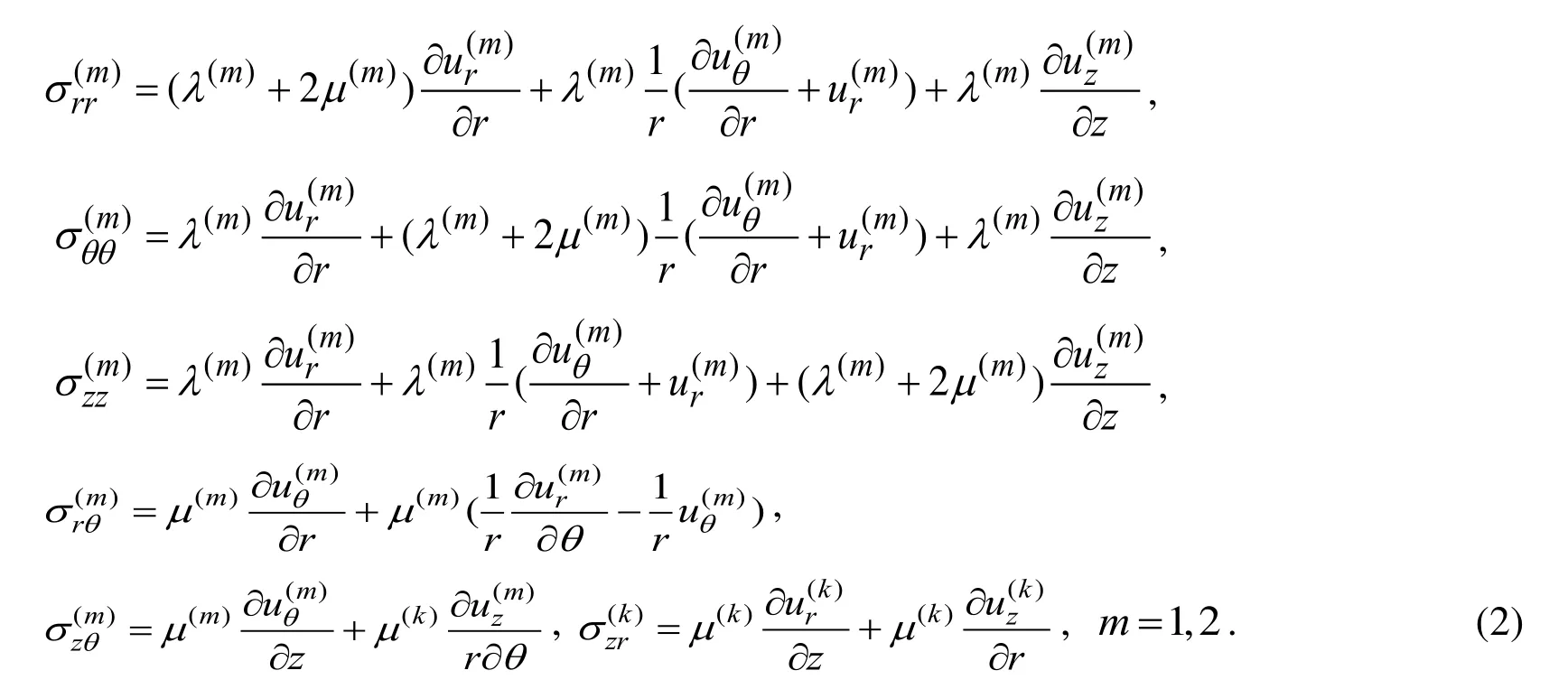
In the relations (1) and (2) the conventional notation is used.

According to the foregoing assumptions and to Fig. 1b, we can write the following boundary conditions on the interior surface of the hollow cylinder.

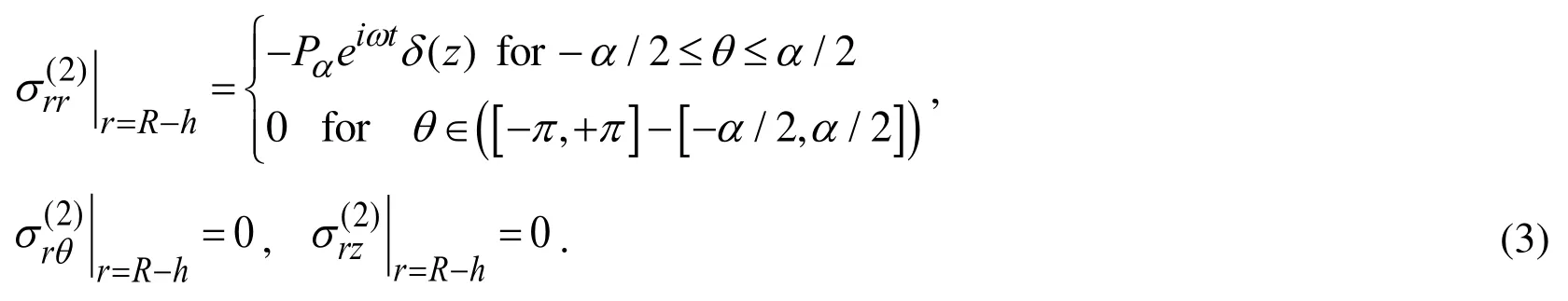
where Pαis determined from the following relation.

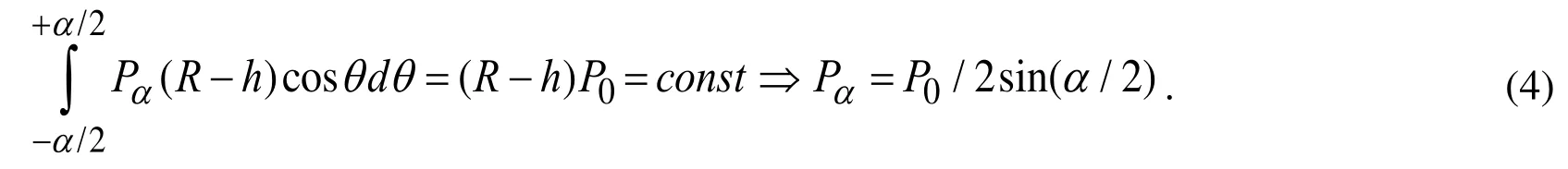
The relation (4) means that the vertical component of the summation of the external forces does not depend on the angle α (Fig. 1b) and this summation is constant.

We assume that the perfect contact conditions satisfy and these conditions are written as follows.

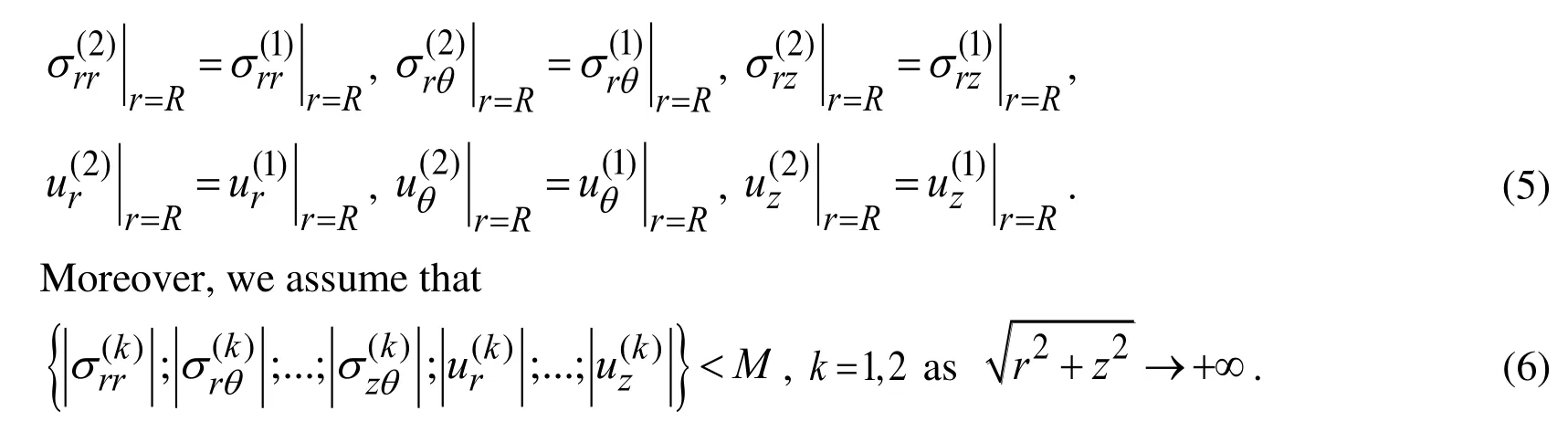
With this the problem formulation is completed.

3 Method of solution

For solution to the boundary value problem (1-6) we use the following representation described in the monograph by Guz [Guz (1999)].

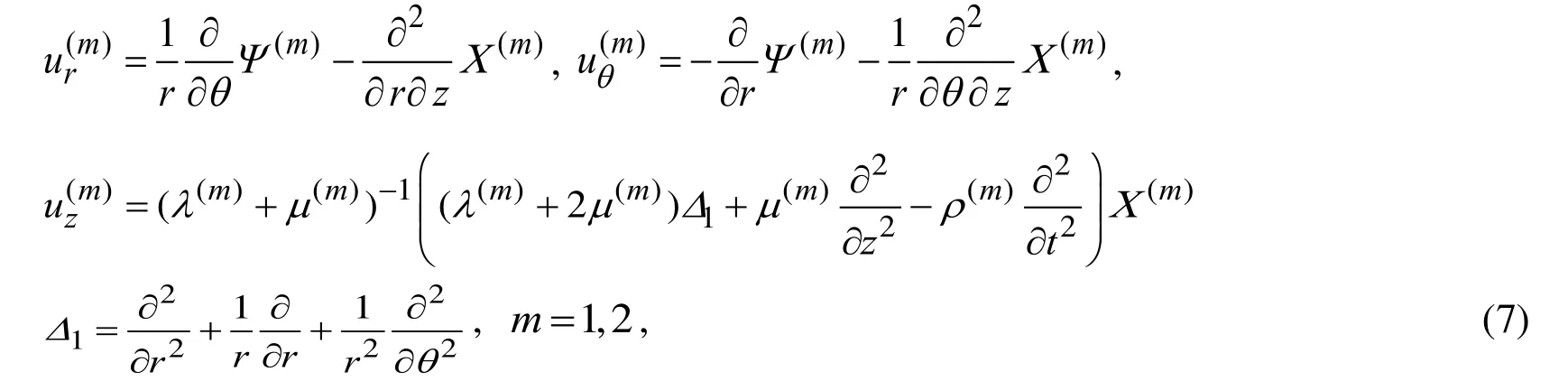
where the functions()mΨand()mХare the solutions to the equations given below.

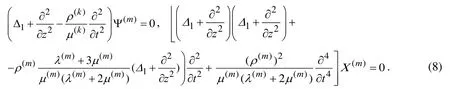
According to the time-harmonic character of the problem, we can use the presentationwhere (,,)r zθis an amplitude of the sought values. Below,we will omit the over-bar on the amplitudes. Thus, according to this presentation, we can replace the operatorsespectively and obtain the equations, relations, boundary and contact conditions for the amplitudes of the sought values from the forgoing equations. Further, we apply the exponential Fourier transformwith respect to the coordinate z (where s is a transform parameter)to all the equations, relations, boundary and contact conditions obtained for the amplitudes.

Thus, according to the foregoing discussions and according to the symmetry and asymmetry of the amplitudes of the sought values with respect to the 0z=plane their original can be presented through their Fourier transform by the following expressions.

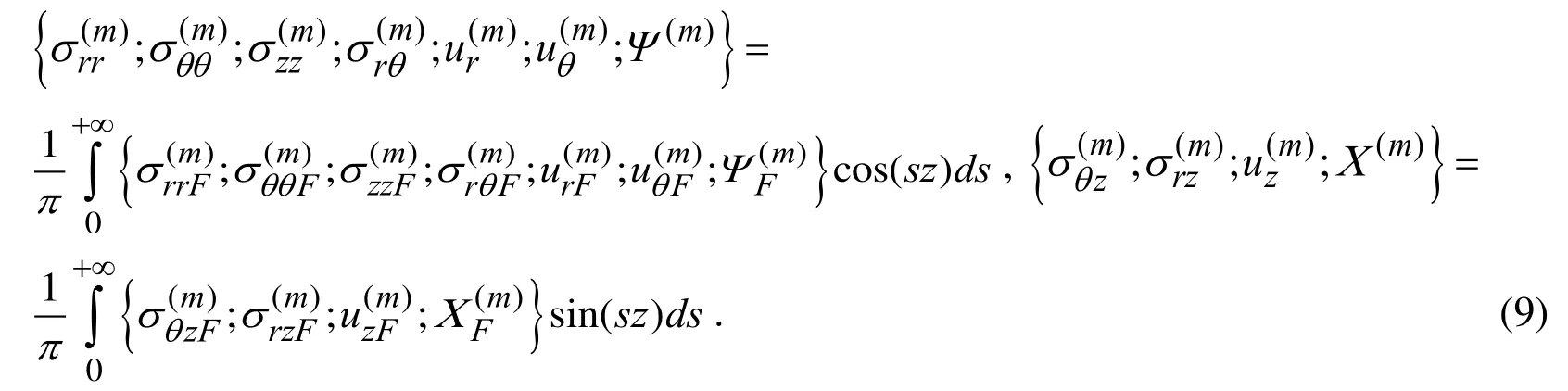
We use the dimensionless coordinates ' /r rh=and ' /z zh=(the upper prime will be omitted below) and introduce the notation

Thus, substituting the expressions in (9) into the foregoing equations and relations, and taking the notation (10) into consideration we obtain the following equations for the functionsand:

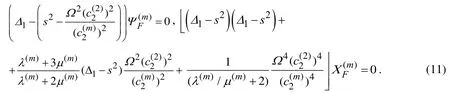
Taking the periodicity of the sought quantities with respect to the θinto account we can represent the functionsandin the Fourier series form as follows.

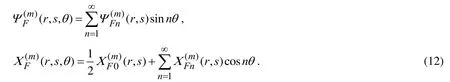
Substituting expressions in (12) into the equations in (11) we obtain the equations given below for the unknown functions(,)rsand(,)rs.

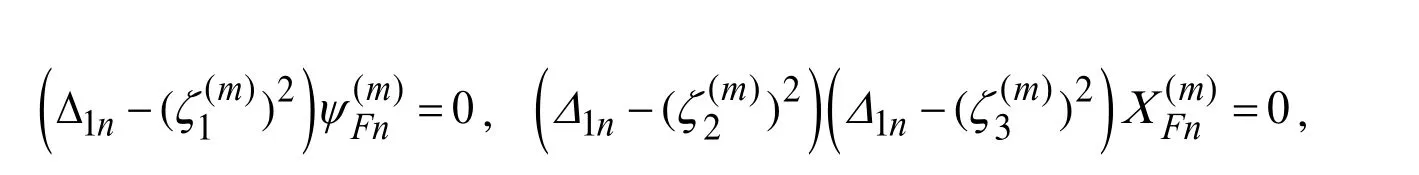
In (13), the unknown constants2and2are determined as solutions of the following equation.

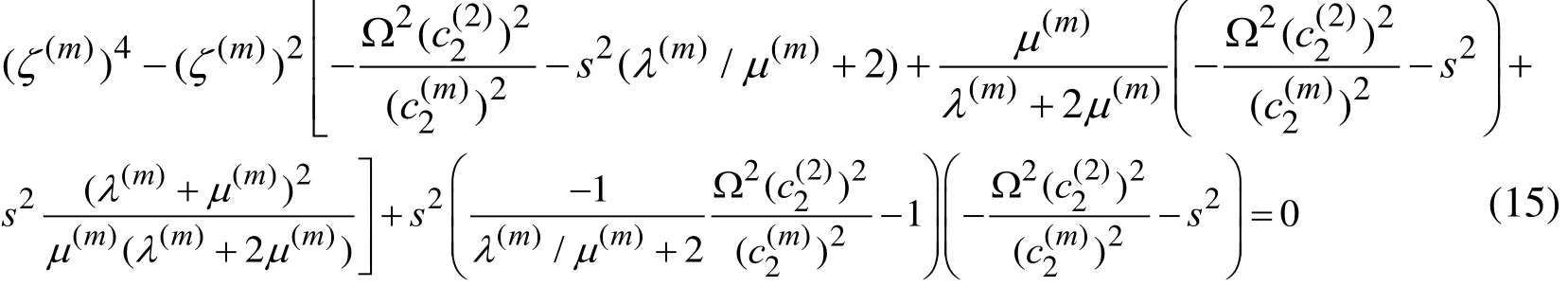
Taking the condition in Eq. (6) into consideration, we find the solution to equations in (13)as follows.

For the hollow cylinder:

Substituting the expressions in (16), (17) and (9) into the Fourier transform of the equations in (9) and (2), we obtain the expressions for the Fourier transforms of the stresses and displacements which enter into the boundary (3) and contact (5) conditions. To reduce the volume of the paper, here we do not give these expressions.

It follows from the expressions of the boundary (3) and contact (5) conditions that the second and third conditions in (3), and all the contact conditions in (5) remain valid as are for the corresponding transforms. However, the first condition in (3) is transformed to the following one

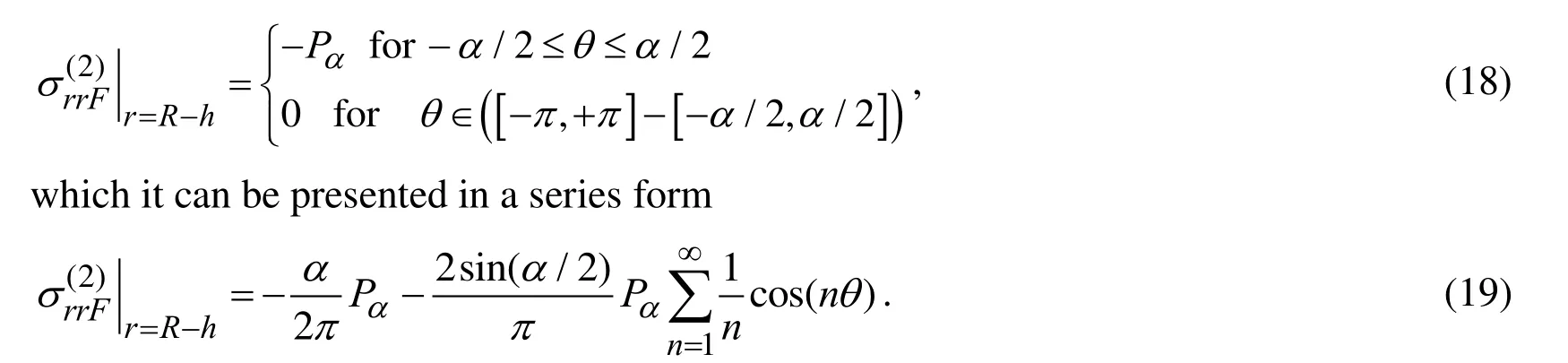
In this way, substituting the expressions obtained through the relations (2), (7) and (12)into the boundary (3) and contact (5) conditions we obtain the equations for the abovenoted unknown constants. Also, to reduce the volume of the paper, here we do not give these equations.

After finding the aforementioned unknown constants from the above-noted equations, we determine completely the Fourier transformation of the sought values and applying the algorithm which will be detailed below, the originals of these values are determined through the calculation of the integrals given in (9).

4 Numerical results and discussions

In the present section first we note some remarks on the calculation algorithm of the integrals in (9).

4.1 Some remarks on the algorithm for calculation of the integrals in (9)

According to the Eqs. (9) and (20), the following approximate expression can be written for the stress

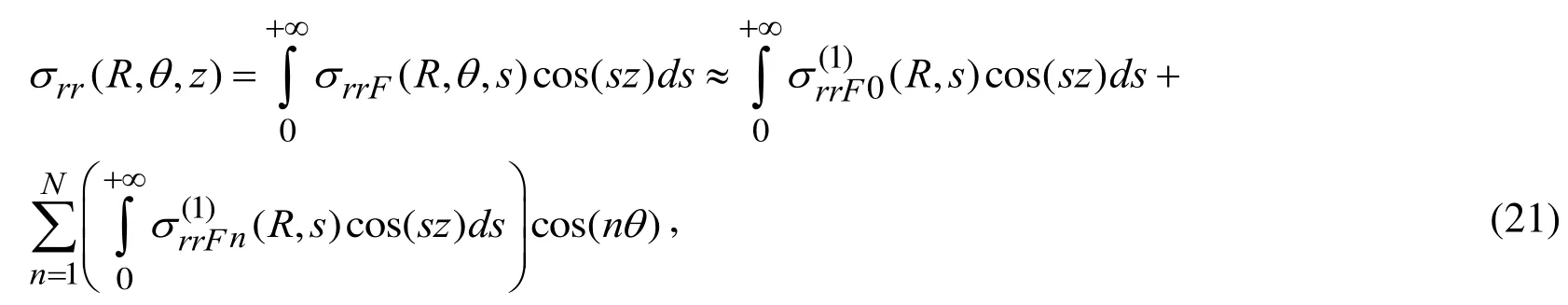
Note that under writing the relation (20) the infinite Fourier series is replaced by thecorresponding finite one and the number of terms in this finite series, i.e. the number in (20) is determined from the convergence requirement of the numerical results. Moreover note that, according to the solution procedure discussed in the previous section, the unknowns,,,,,,andare determined separately for each selectedfrom the corresponding complete system of equations obtained forand for. Denoting bythe determinant of the matrix, the elements of which are the coefficients of the unknowns in these equations,we can conclude that the equation

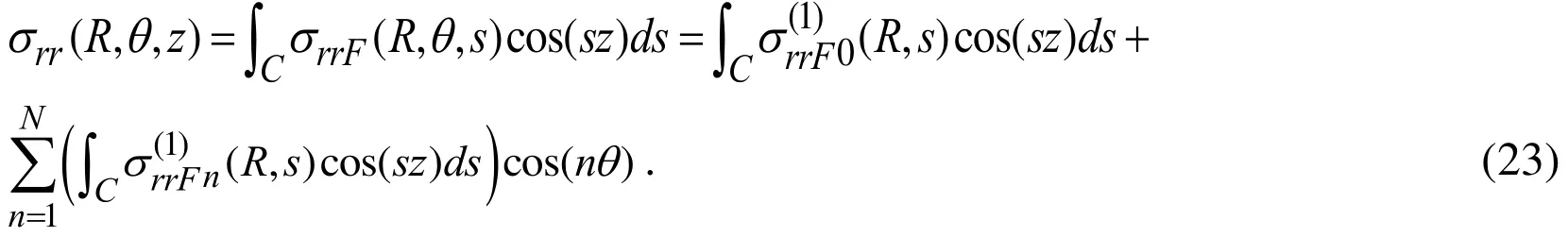
Taking the configuration of the contourgiven in Fig. 1c into consideration, assuming thatdoing some mathematical manipulations we obtain the following expressions for calculation of the stress

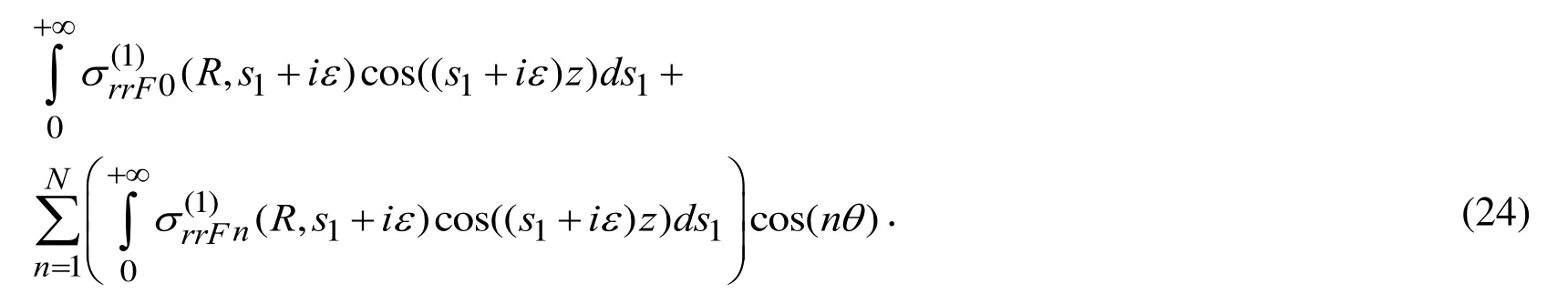
Note that in the calculation procedure the improper integrals with the formare replaced with the corresponding definite integrals with the formand the values ofare defined from the corresponding convergence requirement. Moreover, note that under calculation these definite integrals, the intervalvided into a certain number (denote this number through) of shorter intervals and within each of these intervals, the integrals are calculated by the use of the Gauss algorithm with ten integration points. The values of the integrated functions at the integrated points are defined through the solution of the corresponding equations obtained from the boundary and contact conditions and all these procedures are performed automatically in the PC by use of the corresponding programs constructed by the authors of the paper in MATLAB.

4.2 Testing the calculation algorithm

Now we attempt to test the foregoing calculation algorithm with respect to the numberof the shorter intervals, with respect to thewhich is the upper value of the integration interval in Eq. (24) and with respect to the numberwhich indicates the number of terms selected in the Fourier series in Eq. (24). Under all calculation procedures we assume thatwhich is also determined according to the convergence requirement of the numerical results. This latter question is detailed in the monograph by Akbarov [Akbarov(2015)] and therefore here we don’t consider it again.For aforementioned testing we consider the case where the materials of the cylinder and surrounding elastic medium are real ones, i.e. we assume that that the material of the cylinder is Steel with the mechanical constantsand the material of the surrounding elastic medium is Aluminum with the mechanical constantssymbols,andindicate the material density, Poisson’s ratio and shear modulus respectively. Assume thatand.Thus, we consider the results given in Fig. 2a which are obtained for the above selected materials and illustrate the convergence of the numerical results related to the frequency response of the interface normal stress(24) with respect to the number . Note that these results are obtained.

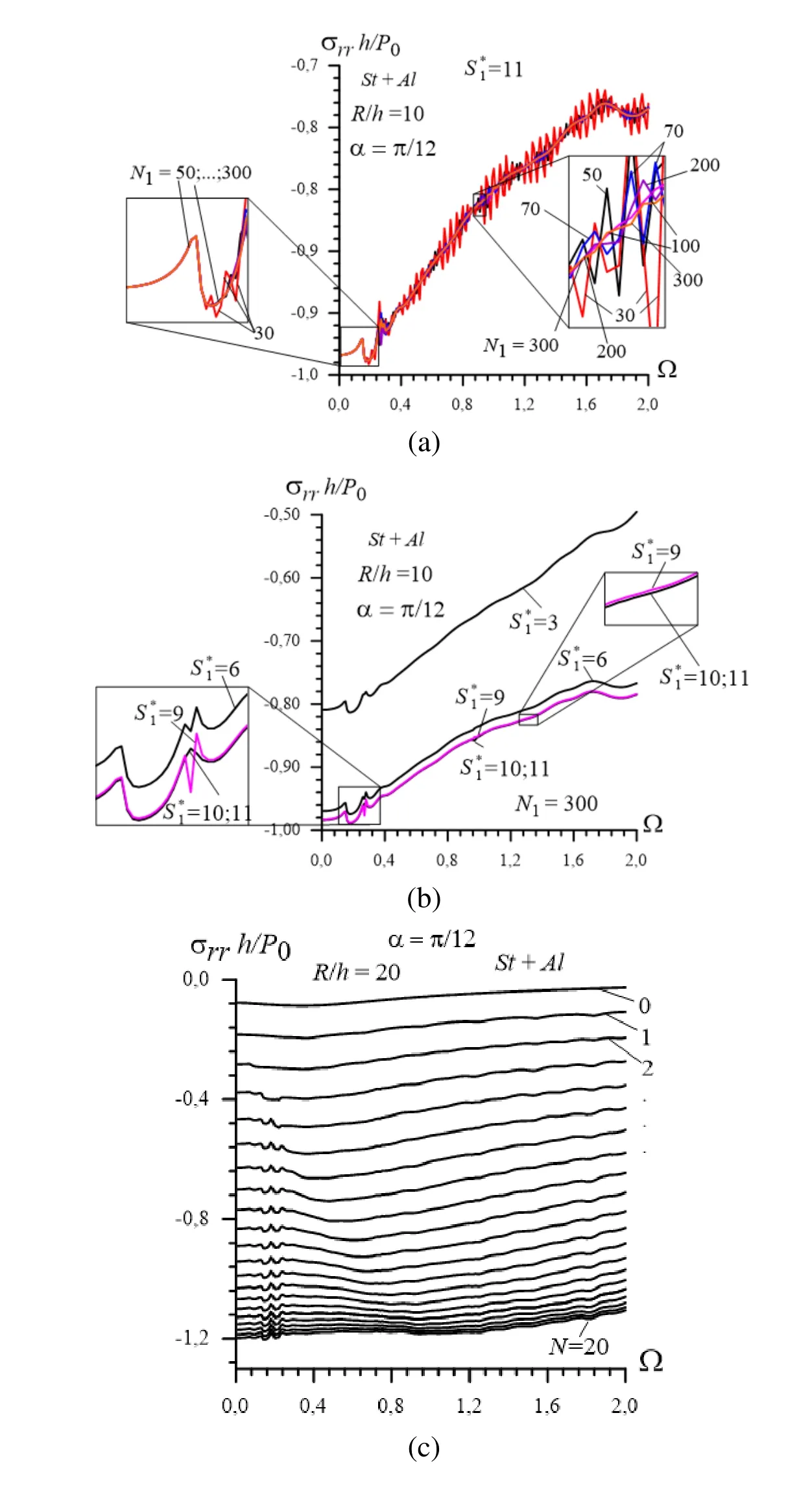
Figure 2: Convergence of the numerical results with respect to the number(a); with respect to the(b) and with respect to the numberin the finite series presentation(24)

Consider also the results illustrated the convergence of the numerical results with respect to the value of the. These results are given in Fig. 2b which are obtained in the case whereand. It follows from these results that in the cases wherenumerical results are convergent with accuracy.

Finally, we consider numerical results givenin Fig. 2c which illustrate the convergence ofthese results with respect to the number in the case where underand. The comparison of the results obtained for various values of the numbershows that these values are converge to the certain limit ones and the difference between the results obtained in the case whereandis not more than.

Thus, taking into consideration of the foregoing testing and other ones which are not given here we can conclude that the calculation algorithm used in the present investigation is sufficiently guaranteed one. Moreover, taking into consideration of the foregoing results into consideration under the obtaining all the numerical results which will be discussed below it is assumed that,and.

4.3 Numerical results on the frequency response of the interface normal stresses

We investigate the frequency response of the interface normal stressdetermined by the expression (24). First of all, we note that the main parameter which distinguishes the problem under consideration from the corresponding problems related to the system "covering layer +half-space", which are detailedin the monograph by Akbarov[Akbarov (2015)] and others listed therein, is the parameter Therefore in the present investigation, the main attention is focused on the influence of the ratio on the studied frequency responses for the selected pairs of materials for the constituents of the system "hollow cylinder+surrounding elastic medium". Below we will assume that(if otherwise not specified) and consider the frequency responses of the interface normal stress

First we consider the case where the material of the cylinder is Steel and the material of the surrounding elastic medium is Aluminum. The graphs illustrated the frequency response of the stressin this case are given in Fig. 3. These graphs are constructed for various values of the ratio and it follows from those that the absolute values of the stress decrease with decreasing of the ratio Moreover, it follows from these graphs that the dependence between the stressand dimensionless frequencyhas complicated character. For instance, these graphs in the vicinity of certain values of the frequencyhave "ascent-descent" character. Apparently, the "ascent-descent" cases in the graphs are caused by the wave reflections from the interface surface between the cylinder and surrounding elastic medium.

We also note the following statement which follows from the graphs givenin Fig. 3. In therelatively small values of the ratio (for instance, in the cases where 5)the absolute values of the stress in the dynamical loading case, in general, are less than the corresponding value of this stress in the static loading case, i.e. in the case where.However, in the relatively great values of the ratio for instance, in the cases where and 20) the mentioned above rule violates in a certain value of the frequency.If to say more precisely, this violation takes place only in the first "ascent-descent" case in the corresponding graphs.

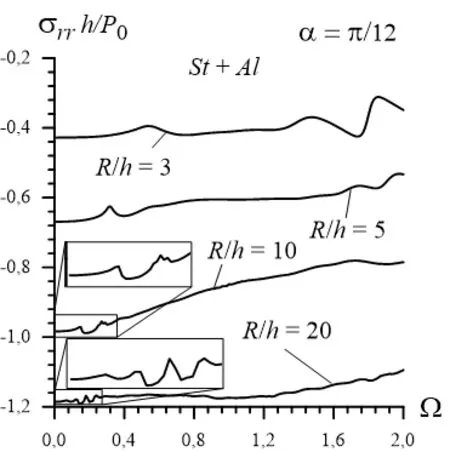
Figure 3: Frequency response of the stress for the system

We recall that the foregoing analysis relates to the case where the material of the cylinder is Steel and the material of the surrounding elastic medium is Aluminum and the ratio of the modulus of elasticity of the Aluminum (denote is by) to the modulus of elasticity of the Steel (denote it by) is 0.345, i.e.. Numerical results show that the character of the frequency responses depends significantly not only on the values of the ratiobut also on the ratioFor analysis the influence of the ratioon the character of the frequency responses we consider the corresponding results obtained in the cases where0.5; 0.8; 1.0; 1.5 and 2.0 and given in Figs.4, 5, 6, 7 and 8 respectively. Under construction the graphs given in these figures it is assumed that

It follows from Fig. 4 that under relatively great value of the ratiothere are many cases under which the absolute values of the stress become significantly greater than that obtainedin the static loading case, i.e. in the case where. For instance, in the case where after some "ascent-descent" cases the graphs becomes smooth nonmonotonic and in the absolute maximum value of the stress in this non-monotonic part is greater significantly than that obtained in the corresponding static loading case. Fig. 4 alsoshows that in the relatively small values of the ratio (for instance in the case where absolute maximum value of the stress has sharp increase in a certain value of the vibration frequency.

We analyze also how the future increase in the value of the ratioinfluences on the frequency responses obtained in the various values of the For this purpose, we consider graphs given in Fig. 5 which are constructed in the case where.It follows from these graphs that in the case under considerationthe "period" of the "ascent-descent" cases increase with decreasing the values of the ratio Moreover, it follows from these graphs that in the "global" sense (i.e. the values of the stress regarding the points on the corresponding smooth lines which are obtained from the corresponding graph through the fit of that by the use of polynomial with the degree 10) the dependence between the stress and frequency has non-monotonic character. According to this character, before a certain value of the frequencyan increase of thecauses an increase in the absolute values of the stress and after this "certain" frequency, vice versa, an increase in the values of the frequencycauses a decrease in the absolute values of the stress. It should benoted that this rule is violated in the case where . Nevertheless, the nonmonotonic character of the frequency response plays a dominant role also in the case where.

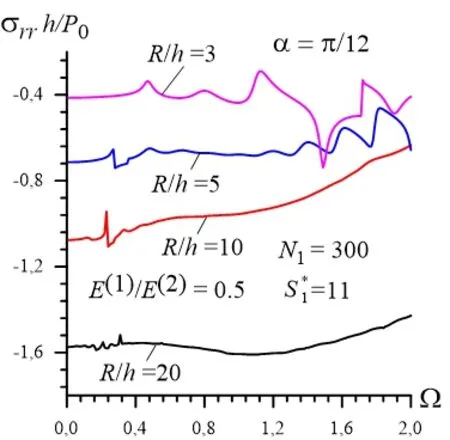
Figure 4: Frequency response of the stress for the system for which

Thus, it follows from the foregoing results that the future increase in the value of the ratioauses to increase significantly the absolute values of the interface normal stress with respect to the corresponding static stress. This conclusion is also confirmed with the results illustrated in Fig. 6 which relate to the case whereows from these results that the dependence between the stress and frequency has non-monotonic character and this non-monotonic character is not in the "global" sense as in the case where, this character is followed directly from the graphs given in Fig. 6.Moreover, it follows from these results that these graphs have not any "ascent-descent"parts. Consequently, the change of the stress with respect to the frequency in the case wheresmooth. This statement proves again that the "ascent-descent" parts in the graphs obtained in the cases wherel be detailed below such pats appear also in the corresponding graphs obtained for the cases whereare caused by the wave reflection from the interface surface between the constituents of the system under consideration.

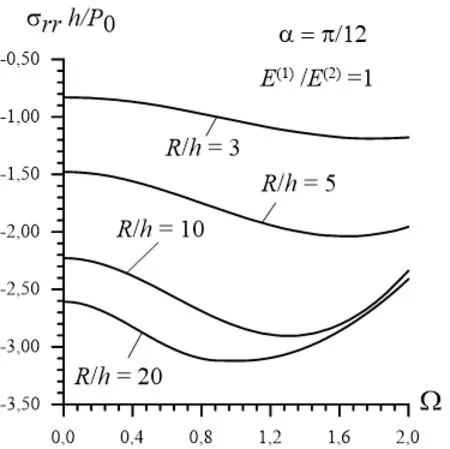
Figure 6: Frequency response of the stress for the system for which

Besides all of these, we recall the fact that in the works by Lamb [Lamb (1904)], Gladwell[Gladwell (1968)] and Johnson [Johnson (1985)] the similar non-monotonic character of the frequency responses is also obtained for the time-harmonic dynamic problem related to the homogeneous isotropic half-space. Further, in the monograph by Akbarov [Akbarov(2015)] and in the works listed therein, this fact is also examined for the time-harmonic dynamic problems for the plane-layered systems. Consequently, the results given in Fig. 6 agree in the quantitative sense with the results obtained in the works by Lamb [Lamb(1904); Gladwell (1968); Johnson (1985); Akbarov (2015)] and it is confirmed that under time-harmonic loading in a certain part of the cylindrical hole the frequency response of the stresses, which appear in the infinite elastic medium contained this hole, has nonmonotonic character. Also, the results given in Fig. 6 shows that the values of the frequency under which the absolute values of the stress has its maximum, increase with decreasing of the ratio

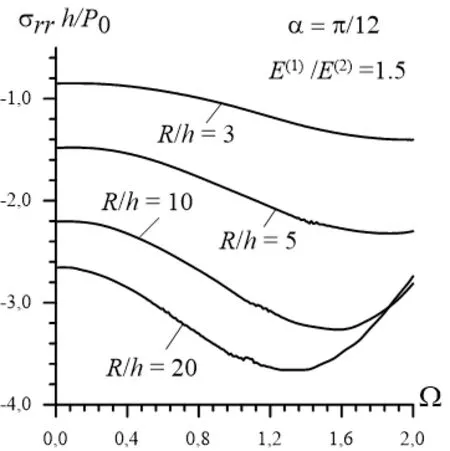
Figure 7: Frequency response of the stress for the system for which

Now we consider the results given in Figs. 7 and 8 which are obtained in the cases whereand 2.0, respectively. It follows from these results that frequency responses obtained in the cases wheresimilar with the corresponding ones obtained in the case where, in the cases wherethe graphs of the frequency responses have also the "ascent-descent" pats which are very insignificant than those obtained in the cases whereConsider numerical results related to the distribution of the normal stress with respect tothe coordinates andtheexamples for which are given in Figs. 9 and 10. These results are obtained for the system in the case where.The values of the other parameters are shown in the figures field. It follows from these results that the absolute values of the stress are decay with the distance of the part at which the external forces act.Moreover, it follows from Fig. 10 that the absolute values of the stress decrease with increasing of the angle.

Comparison of the present results with the corresponding ones obtained in the paper by Akbarov et al. [Akbarov and Mehdiyev (2017)] shows that the absolute maximum values of the normal stress obtained in the present case are greater significantly than corresponding ones obtained in the axisymmetric loading case.

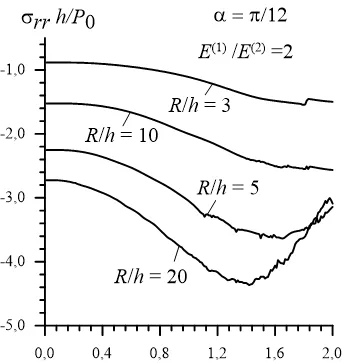
Figure 8: Frequency response of the stress for the system for which

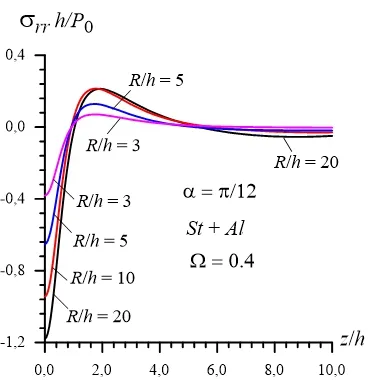
Figure 9: Distribution of the stress with respect to the coordinate

5 Conclusions

Thus, in the present paper within the scope of 3D exact equations and relations of elastodynamics the analytical-numerical method of solution is developed and employed for the analysis of the non-axisymmetric dynamic stress state in the system consisting of the hollow cylinder and surrounding elastic medium. Numerical results on the frequency response of the interface normal stress are presented and discussed. These results illustrate the character of the influence of the mechanical and geometrical parameters of the considered system on the values of the amplitude of the mentioned stress.

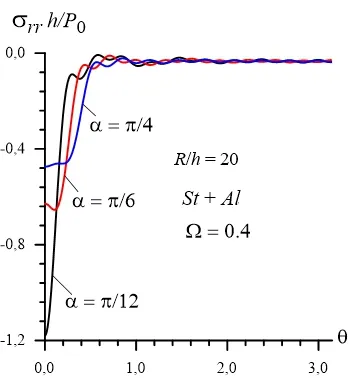
Figure 10: Distribution of the stress with respect to the coordinate

Thus, according to these results the following concrete conclusions can be drawn:

· The absolute values of the interface normal stress increase with the ratio of the external radius of the cross section of the hollow cylinder to its thickness;

· In the case where the modulus of elasticity of the cylinder material is greater significantly than that of the surrounding elastic medium (i.e. in the cases wheremodulus of elasticity of the surrounding medium (of the hollow cylinder) material), the character of the frequency responses of the stress under consideration have complicated character and these responses are accompanied by "ascent-descent" parts which is caused with the reflection of the waves from the materials interface;

· In the case where the modulus of elasticity of the cylinder material is greater slightly, than that of the surrounding material (for instance, in the case where, the frequency responses have non-monotonic character in the global sense;

· In the case where the materials of the constituents of the system under consideration are the same (i.e. in the case whereresponses have smooth non-monotonic character, i.e. for each selected ratio of the cylinder's cross section radius to its thickness there exists such value of the frequency, under which the absolute value of the stress has maximum;

· The aforementioned non-monotonic character of the frequency response occurs also in the cases where the modulus of elasticity of the cylinder's material is less(i.e. in the cases wherthe surrounding elastic medium;

· The absolute maximum values of the normal stress obtained in the present case are greater significantly than corresponding ones obtained in the axisymmetric loading case [Akbarov and Mehdiyev (2017)].

Abdulkadirov, S. A. (1981): Low-frequency resonance waves in a cylindrical layer surrounded by an elastic medium. Journal of Mining Science, vol. 80, pp. 229-234.

Akbarov, S. D. (2006a): Dynamical (time-harmonic) axisymmetric interface stress field in the finite pre-strained half-space covered with the finite pre-stretched layer.International Journal of Engineering Science, vol. 44, pp. 93-112.

Akbarov, S. D. (2006b): On the dynamical axisymmetric stress field in a finite prestretched bi-layered slab resting on a rigid foundation. Journal of Sound and Vibration, vol.294, pp. 221-237.

Akbarov, S. D. (2013): On the axisymmetric time-harmonic Lamb’s problem for a system comprising a half-space and a covering layer with finite initial strains. Computer Modeling in Engineering & Sciences, vol. 70, pp. 93-121.

Akbarov, S. D. (2015): Dynamics of pre-strained bi-material elastic systems: Linearized three-dimensional approach. Springer, New-York.

Akbarov, S. D.; Guler, C. (2005): Dynamical (harmonic) interface stress field in the halfplane covered by the prestretched layer under a strip load. The Journal of Strain Analysis for Engineering Design, vol. 49, no. 3, pp. 225-236.

Akbarov, S. D.; Ilhan, N. N. (2010): Time-harmonic dynamical stress field in a system comprising a pre-stressed orthotropic layer and pre-stressed orthotropic half-plane. Archive of Applied Mechanics, vol. 80, pp. 1271-1286.

Akbarov, S. D.; Ilhan, N. (2013): Time-harmonic Lamb’s problem for a system comprising a piezoelectric layer and piezoelectric half-plane. Journal of Sound and Vibration, vol. 332, pp. 5375-5392.

Akbarov, S. D.; Mehdiyev, M. A. (2017): Forced vibration of the elastic system consisting of the hollow cylinder and surrounding elastic medium under perfect and imperfect contact.Structural Engineering and Mechanics, vol. 62, pp. 113-123.

Babuscu Yesil, U. (2017): Forced and Natural Vibrations of an Orthotropic Pre-Stressed Rectangular Plate with Neighboring Two Cylindrical Cavities. Computers, Materials &Continua, vol. 53, no. 1, pp. 1-23.

Bui, T. Q.; Zhang, X.; Hirose, S.; Batra, R. C. (2016): Analysis of 2-dimensional transient problems for linear elastic and piezoelectric structures using the consecutiveinterpolation quadrilateral element (CQ4). European Journal of Mechanics-A/Solids, vol.58, no. pp. 112-130.

Fan, Q.; Zhang, Y.; Dong, L.; Li, S.; Atluri, S. N. (2015): Static and Dynamic Analysis of Laminated Thick and Thin Plates and Shells by a Very Simple Displacement-based 3-D Hexahedral Element with Over-Integration. Computers, Materials & Continua, vol. 47, no.2, pp. 65-88

Gladwell, G. M. L. (1968): The calculation of mechanical impedances related with surface of semi-infinite elastic. Journal of Sound and Vibration, vol. 8, pp. 215-219.

Guz, A. N. (1999): Fundamentals of the three-dimensional theory of stability of deformable bodies, Springer, Berlin.

Hasheminejad, S. M.; Komeili, M. (2009): Effect of imperfect bonding on axisymmetric elastodynamic response of a lined circular tunnel in poroelastic soil due to a moving ring load. International Journal of Solids and Structures, vol. 46, pp. 398-411.

Hussei, M. F. M.; François, S.; Schevenels, M.; Hunt, H. E. M.; Talbot, J. P. et al.(2014): The fictitious force method for efficient calculation of vibration from a tunnel embedded in a multi-layered half-space. Journal of Sound and Vibration, vol. 333, pp.6996-7018.

Jensen, F. B.; Kuperman, W. A.; Porter, M. B.; Schmidt, H. (2011): Computational ocean acoustic, 2nded. Springer, Berlin.

Johnson, K. L. (1985): Contact mechanics. Cambridge Univ. Press, Cambridge.

Lamb, H. (1904): On the propagation over the surface of an elastic solid. Philosophical Transactions of the Royal Society of London, vol. 203, pp. 1-42.

Parnes, R. (1969): Response of an infinite elastic medium to traveling loads in a cylindrical bore. Journal of Applied Mechanics, vol. 36, no.1, pp. 51-58.

Parnes, R. (1980): Progressing torsional loads along a bore in an elastic medium.International Journal of Solids and Structures, vol. 36, no. 1, pp. 653-670.

Pozhuev, V. I. (1980): Reaction of a cylindrical shell in a transversely isotropic medium when acted upon by a moving load. Soviet applied mechanics, vol. 16, no. 11, pp. 958-964.Wei, X.; Chen, W.; Chen, B.; Chen, B.; Chen, B. et al. (2016): B-Spline Wavelet on Interval Finite Element Method for Static and Vibration Analysis of Stiffened Flexible Thin Plate. Computers, Materials & Continua, vol. 52, no. 1, pp. 53-71.

Yuan, Z.; Bostrom, A.; Cai, Y. (2017): Benchmark solution for vibration from a moving point source in a tunnel embedded in a half-space. Journal of Sound and Vibration, vol.387, pp. 177-193.