基于磁记忆检测方法的45钢应力集中评价

，， ，， ，

(1.江西省锅炉压力容器检验检测研究院，南昌 330029；2.江西省锅炉压力容器检验检测研究院南昌分院，南昌 330006；3.南昌航空大学 无损检测技术教育部重点实验室，南昌 330063)

通常情况下，铁磁性零部件在承受载荷的过程中会出现残余应力集中的现象，在残余应力集中的区域容易萌生裂纹，而使得铁磁性零部件的使用寿命受到极大的影响[1-2]。金属磁记忆检测技术可以准确地检测出铁磁性材料中的应力集中情况，是目前能够对铁磁构件进行早期诊断的无损检测方法之一[3-4]。该技术具有易于操作、高灵敏度、可靠性好，以及无需考虑提离效应、无需专门进行磁化等特点[5-7]。

笔者基于金属磁记忆效应机理，以静载拉伸试验为检测手段开展研究工作，实现了对45钢试样磁记忆信号的检测，分析了试样磁记忆信号二维分量的信号特征，分析了磁记忆信号微分后合成的李萨如图形的归一化当量与拉伸载荷之间的内在联系，为判别应力集中程度提供了相关依据，可为45钢的磁记忆检测应用提供参考。

1 试件制备及试验方案

试件材料为45钢，试件规格(长×宽×厚)为200 mm×35 mm×2 mm，试件的几何尺寸及检测路径如图1所示。材料的主要性能参数为：屈服强度355 MPa;抗拉强度526 MPa;弹性模量210 000 MPa。在试件两侧预置两个直径为10 mm的U型缺口，中间预设3条长度为60 mm的测量线，测量线之间的间距为5 mm。

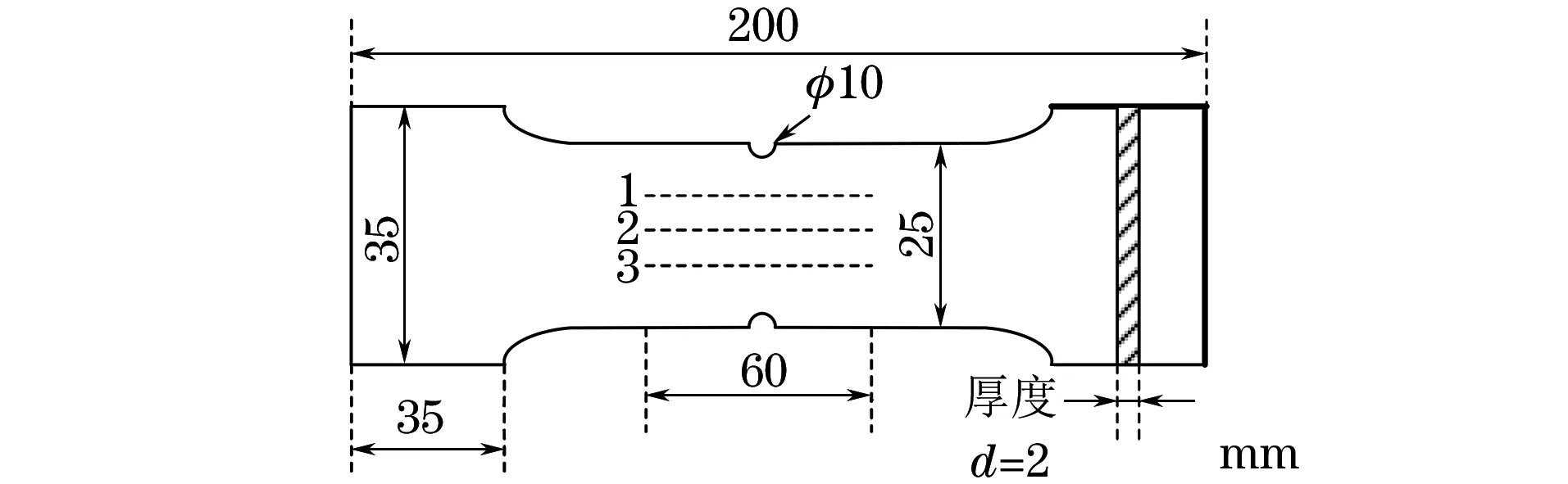
图1 试件几何尺寸及检测路径示意

45钢作为一种高强度钢，含碳量高，无明显屈服阶段，但塑性变形显著，在断裂前会出现明显的缩颈或形变。为了减小各种因素对试件初始磁信号产生的不利影响，采用去应力退火对试件进行处理。

试验所需设备为:① WDW-E100D型电子程控试验机，如图2(a)所示；② LakeShore421弱磁测量仪；③ 实验室自制的磁记忆二维检测装置,如图2(b)所示。

图2 磁记忆信号检测系统装置外观图片

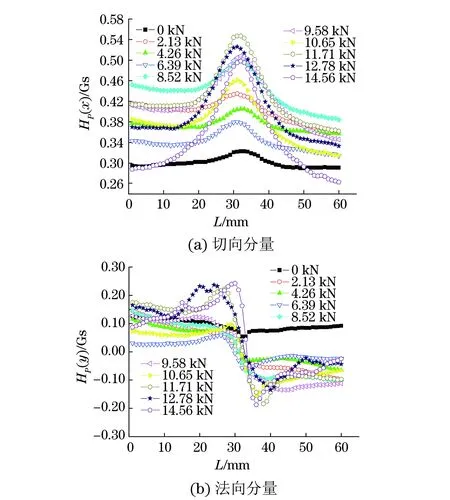
图3 1号测量路径上的磁记忆信号分布曲线

试验过程为:将载荷设定为0.2σs(σs为屈服强度),0.4σs,0.6σs,0.8σs,0.9σs,σs，1.1σs,1.2σs,σb(抗拉强度)进行拉伸试验。当试件处于预定载荷时，弱磁测量探头沿着检测路径测量试件的磁记忆信号二维分量。

拉伸过程中，加载速率设定为0.5 mm·min-1。对于二维检测装置中的磁场测量，为提高检测效率，将采样间距设定为1 mm。

2 检测结果及分析

采用磁记忆二维检测法，对图1所示的1，2,3号测量线上的磁记忆信号二维分量进行检测，得到预定载荷下的磁记忆信号分布曲线,如图3，4，5所示。图中HP(x)为磁记忆信号切向分量,HP(y)为磁记忆信号法向分量。

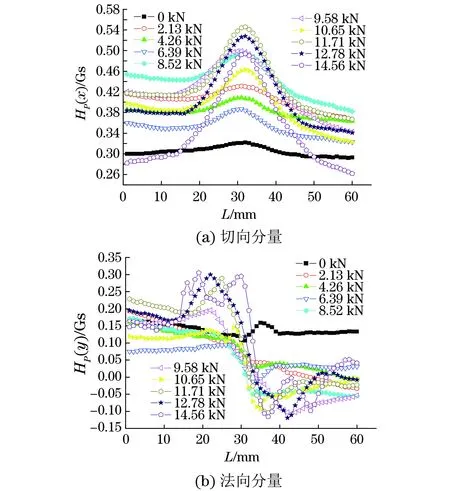
图4 2号测量路径上的磁记忆信号分布曲线

图5 3号测量路径上的磁记忆信号分布曲线

将3条测量线上的磁记忆信号二维分量进行对比，发现试件缺口处的磁记忆信号变化遵循以下规律：当试件未进行加载时，切向分量的分布曲线存在单峰现象，法向分量的分布曲线无特征现象而可近似看成一条直线，进一步表明切向分量与拉伸载荷间的相关性更好；随着拉伸载荷的增大，磁记忆信号切向分量和法向分量的幅值越来越大，特征现象也越来越明显；当拉伸载荷达到弹性阶段末期进入屈服阶段时，切向分量峰值先减小后回升，法向分量幅值也出现同样的变化；当拉伸载荷完全处于塑性阶段时，磁记忆信号二维分量幅值持续递增，特征现象愈发显著。通过观察图3，4，5可以发现，3条测量线上测得的切向分量幅值无明显差异，而法向分量幅值有所不同，其中3号测量线上测得的法向分量幅值最大，应力集中程度最严重，2号测量线上测得的信号数值次之，1号线上的最小。根据磁场理论，应力集中程度越严重的区域，磁记忆信号的幅值越大，但是磁记忆信号是弱磁信号，在进行试验的过程中容易受到各个方面因素的影响，所以，试验测得的磁记忆信号的数据与理论数据存在一些差异。

通过分析和比较可以发现，3号测量线上测得的磁信号特征现象最为显著，通过对磁记忆信号二维分量进行微分处理得到相关分量的梯度，进而合成磁记忆信号的李萨如图形，如图6所示。

图6 U型缺口试件3号测量线上的李萨如图形

从图6可看出，不同拉伸载荷作用下的李萨如图形区域面积的变化具有一定的规律。在初始阶段，区域面积较小，随着载荷的不断增大，形成封闭区域的大小逐渐增大，在屈服阶段附近出现反向减小，之后伴随载荷的继续增大，封闭区域的大小迅速增大。计算的李萨如图形封闭区域的当量面积如表1所示。

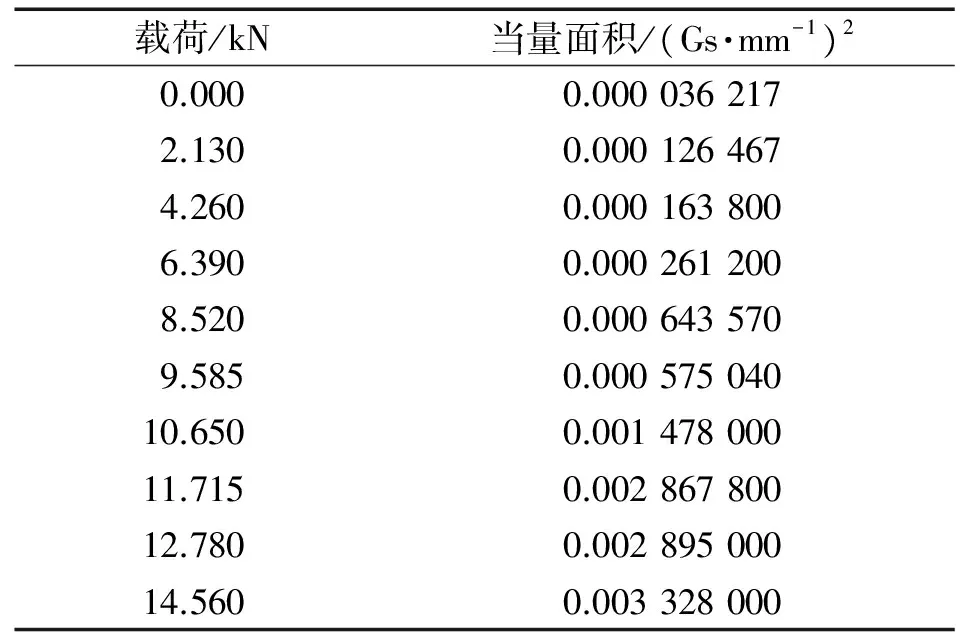
表1 U型缺口试件3号测量线上李萨如图形封闭区域的当量面积

由于求解的李萨如图形封闭区域大小的数量级较低，采用归一化处理方法，对表1中计算出的当量面积进行归一化处理，归一化公式为

(1)

式中:Si为不同应力下的封闭区域大小的当量值；Smax为最大的封闭区域当量面积；Ai为李萨如图形封闭区域的归一化当量。

为了对应力集中程度进行定量化分析，将区域面积进行归一化处理以及非线性拟合，得到归一化当量随载荷变化的非线性拟合曲线，如图7所示。Boltzmann函数回归是一种广义的线性回归方法，具有A2+(A1-A2)/{1+exp[(x-x0)/dx]}的特征方程，其中A1,A2和dx是待求系数。拟合函数中A1=0.062 39，A2=0.974 82，x0=10.754 94，dx=0.653 98，可见相关度Adjusted R-square(相关系数 )为0.973 87，表明李萨如图面积当量与拉伸载荷相关性极好，因此可以利用封闭区域面积当量遵循的Boltzmann曲线对应力集中进行定量分析。

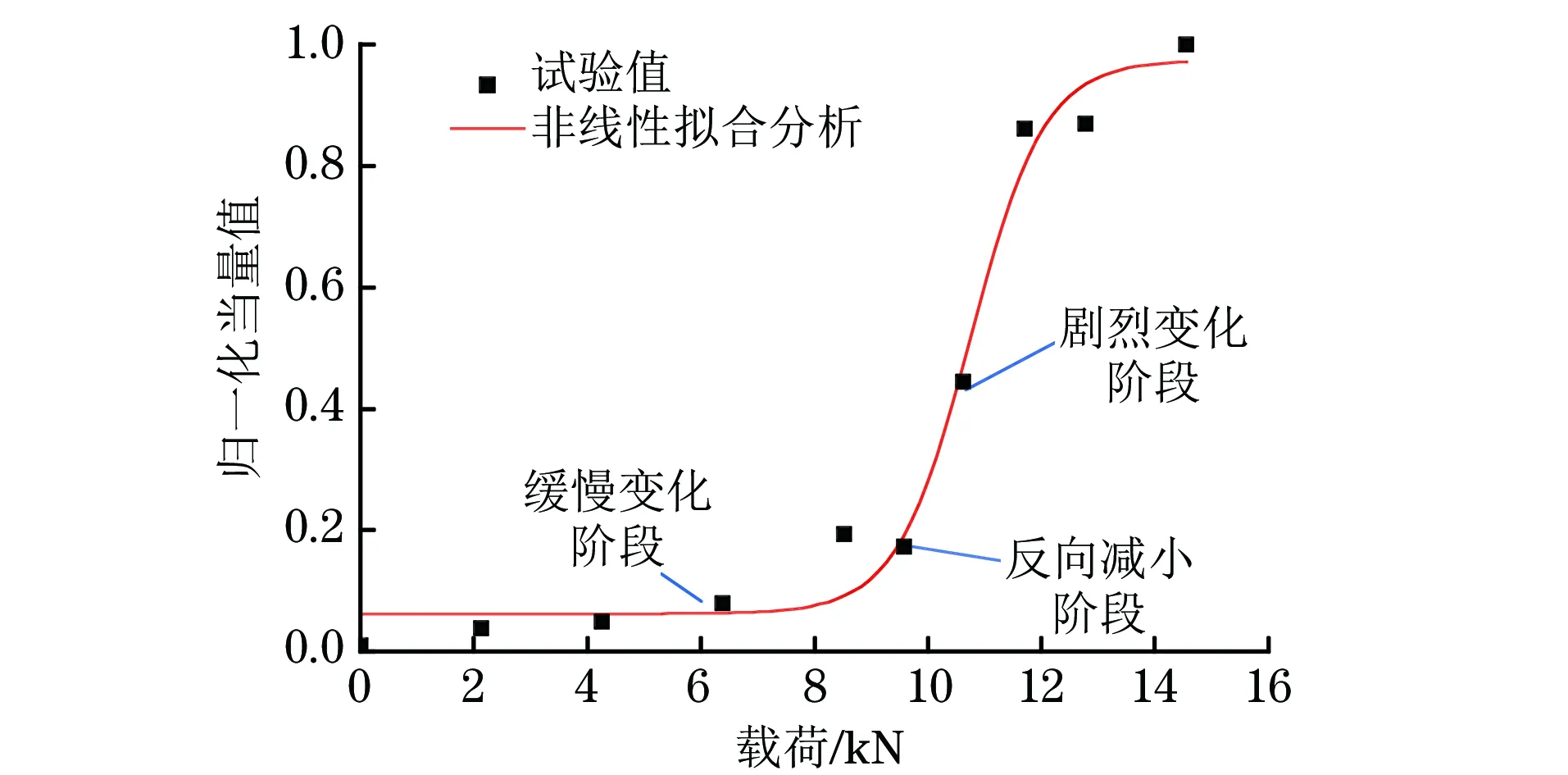
图7 归一化当量值随应力变化的非线性拟合曲线

从图7可看到，归一化当量随应力的变化出现三个阶段:首先是缓慢增长阶段，该阶段从未加载应力至弹性阶段中后期，归一化当量数值较小，一般小于0.2，增长速率较小;第二阶段是反向减小阶段，此阶段为弹性阶段末期至屈服阶段，归一化当量有所减小;第三阶段是剧烈增长阶段，在第三阶段己进入塑性阶段，归一化当量增长速率较大，几乎成倍数增长，向归一化当量值1逼近。

3 结论

(1) 试件受到拉力的不断作用后，在局部缺口附近产生应力集中，此时表面磁记忆信号出现特征现象。其中切向分量分布曲线存在异变峰值，法向分量分布曲线经过零点，因此可用是否出现磁记忆信号特征现象来判定有无应力集中的产生。

(2) 磁记忆信号法向分量分布曲线出现过零点现象时，切向分量磁记忆信号分布曲线都会出现应变峰值现象，而切向分量磁记忆信号出现峰值特征时，法向分量信号可能未过零点。因此表明，对于试件表面的磁记忆信号，切向分量信号与拉伸载荷间存有更好的相关性。

(3) 李萨如图形封闭区域的归一化当量随应力的增大先缓慢增大，当应力进入屈服阶段附近时归一化当量会有所减小，之后随着应力的继续增大，归一化当量又继续增大且增大速率越来越快。可以发现李萨如图形封闭区域的归一化面积与应力间的曲线呈非线性关系，从而可拟合出一条定量判定曲线，利用这一判定曲线可以很好地对应力集中程度进行定量评价。

[1] 任吉林,林俊明.电磁无损检测[M].北京:科学出版社,2008.

[2] DOUBOV A A. Screening of weld quality using the magnetic metal memory effect[J]. 1998, 41:196-199.

[3] DUBOV A A. Development of a metal magnetic memory method[J]. Chemical & Petroleum Engineering, 2012, 47(11/12):837-839.

[4] YANG L J, LIU B, CHEN L J, et al. The quantitative interpretation by measurement using the magnetic memory method (MMM)-based on density functional theory[J].Ndt & E International, 2013, 55(3):15-20.

[5] 任吉林，林俊明，任文坚.金属磁记忆检测技术研究现状与发展前景[J].无损检测，2012, 34(4): 3-10.

[6] 任吉林，王振，饶琪,等.新型磁记忆检测仪器[J]. 无损检测,2013,35(4):70-74.

[7] 任吉林,唐继红,邬冠华,等. 金属的磁记忆检测技术[J]. 无损检测,2001,23(4):154-156.

[8] 黎连修.磁记忆技术若干问题讨论[C]∥第十届全国无损检测大会论文集.南昌:中国机械工程学会,2013.

[9] 任吉林，王进，范振中,等. 一种磁记忆检测定量分析的新方法[J]. 仪器仪表学报,2010,31(2):431-436.

[10] 王丹，董世运，徐滨士,等.静载拉伸45钢材料的金属磁记忆信号分析[J].材料工程,2008(8):77-80.

[11] 唐继红，潘强华，任吉林,等.静载拉伸下磁记忆信号磁记忆变化特征分析[J].仪器仪表学报，2011,32(2):336-340.

[12] 孙玉江,樊建春,徐鹏谊. 基于磁记忆检测的钻具螺纹修扣前后应力集中程度的评价[J]. 无损检测, 2014,36(5):6-10.

[13] 于敏, 缑瑞宾, 仇飞,等. 静载拉伸过程中Q235钢屈服行为与磁畸变关系研究[J]. 热加工工艺, 2017,46(10):90-93.

[14] 胡斌,李运涛. 风电塔筒凹陷的磁记忆检测[J]. 无损检测,2016,38(11):34-36.