Data decomposition method for full-core Monte Carlo transport–burnup calculation

Hong-Fei Liu•Peng Ge•Sheng-Peng Yu•Jing Song•Xiao-Lei Zheng

1 Introduction

In typical transport–burnup calculations,approximately 2000 nuclide species are involved in precise burnup evaluations,wherein approximately 300 nuclides carry nuclear cross-section data,and their reaction rates are tallied in transport simulations.In addition,for each burnup area,the decay constants of all nuclides—obtained from the decay library—are considered in burnup calculations.Three-dimensional high- fidelity full-core models,such as the benchmark for evaluation and validation of reactor simulations(BEAVRS)[1]model,involve millions of burnup areas,which require hundreds of gigabytes of memory.Memory consumption of this magnitude is usually too large for computing nodes even in supercomputer centers.Consequently,the full-core Monte Carlo transport–burnup calculation is highly restricted by its massive memory consumption[2].

Two parallel computing methods,namely domain decomposition and tally data decomposition,have been reportedly used to address the memory consumption problem mentioned above[3].The domain decomposition method decomposes the model geometry into a number of small regions.It then assigns these small regions as local regions to different processes.Each process performs the transport–burnup calculation within its local region.In this method,particles that traverse across the boundary of a local region undergo the corresponding being process performed in the adjacent region.The domain decomposition method,however,has drawbacks,such as inconsistent variance[4],load imbalance,and low parallel ef ficiency.Romano[5,6]proposed the ‘tally server’data decomposition method for Monte Carlo transport simulations,wherein the basic idea is to divide the parallel processor into a computing unit and a storage unit(called tally servers).The computing unit is solely responsible for particle transport simulations,while the storage unit is responsible for the accumulation and storage of tallies.Liang[7]proposed an improvement to this method.He suggested that the tally accumulators be decomposed and stored in equal amounts with each processor being responsible for both particle transport simulation and tally accumulation(including sending and receiving of tracklength-based flux).This peer-to-peer processor relationship makes the program more suitable for large-scale memory taxing Monte Carlo transport–burnup calculations.However,Liang also mentioned in his paper that the material data in each process also occupies a lot of memory and is not decomposed.When the number of burnup areas add up to a million,the material data occupy approximately 4.8 GB per process.Assuming that each hyper-node has 20 processes,the material data would occupy 96 GB of memory,which becomes a factor limiting the utility of Monte Carlo transport–burnup calculations.Shared memory can reduce data redundancy[8],however,combining it with the tally data decomposition method leads to thread race and communication con flicts[9].

In this paper,study of a parallel computing method for full-core Monte Carlo transport–burnup calculations is presented along with the development of a thread-level datadecomposition method to solveaforementioned problems.The proposed method was implemented based on the super Monte Carlo program for nuclear and radiation simulation(SuperMC)[10,11]developed by the FDS Team[12–14].Memory consumption and calculation ef ficiency were tested with a typical pressurized water reactor(PWR)burnup assembly and BEAVRS model.

2 Methods

2.1 Thread-level data decomposition

The tally data decomposition method employs a ‘divide and conquer’strategy,wherein tasks are divided into different subtasks to be resolved separately,and some rules are established to ensure correctness of results.This method is illustrated in Fig.1.

The thread-level data decomposition method has been improved on the lines of the data decomposition method of Liang—(1)the tally accumulators are managed by the thread,instead of the process previously;(2)multi-thread technology is used to share material data in one process thereby reducing data redundancy;(3)solved resource competition of memory access and communication caused by combining multi-thread memory sharing and data decomposition.

In Monte Carlo transport–burnup calculations,memory consumption mainly arises because of three types of data—geometry and material data used to describe the model,nuclear cross-section data,i.e.,particle data used in transport calculations,and data concerning burnup areas including reaction rate tallies.The tallies of nuclide reaction rates account for maximum memory consumption due to presence of millions of burnup areas.In burnup calculations,burnup areas are relatively independent of each other,and these tallies use the same data structure in the program thereby making remote accumulating operations practical.In this work,burnup areas are decomposed equally among different threads using MPI[15]along with OpenMP[16].For materials,geometry,nuclear cross-section data,and so on,the proposed method uses OpenMP to share them within a process.As such,different threads could read the same material,geometry,and nuclear crosssection data thereby signi ficantly reducing memory redundancy.Particle data is relatively independent and takes up less memory;as such,it is allocated to different threads by MPI+OpenMP.

Themain partscomprising thethread-leveldata decomposition are tally decomposition,communication,and accumulation,which are different compared to other data decomposition methods and are shown by red dotted boxes in Fig.2.To avoid MPI calls that are too frequent and increase communication ef ficiency,the tallies generated by each particle are initially stored in a message buffer.At the end of the particle history,the tally buffer,if full,is cleared,and the information stored therein is sent to corresponding thread via non-blocking MPI calls.

2.2 Tally communication

Tally data are transferred using the message-passing interface(MPI),which is a communication protocol in parallel programming.A virtual channel in MPI is uniquely identi fied by tuples(c,s,t)(communicator,source,tag)on the receiver side and(c,r,t)(communicator,receiver,tag)on the sender side.False matching can be avoided by using different tags(or communicators)for each thread[9].Thus,different threads in one process that simultaneously communicate with threads in another process with the same tag,source,and communicator will lead to a con flict as shown in Fig.3a.This can be attributed to the same message matching mechanism being used.

Fig.1(Color online)a Serial computing,b parallel computing,c parallel computing of tally data decomposition

Fig.2 Process work flow of thread-level data decomposition

To resolve this con flict,a fine-grained positioning mode is proposed.Two rules have been de fined for sending and receiving messages—(a)each thread can only receive one tag,and(b)messages that target different threads should be de fined using different tag values.With these rules(shown in Fig.3b),messages can be sent directly from one thread to anotherwithoutany con flict,which signi ficantly improves communication ef ficiency.

2.3 Tally accumulation

In thread-level data decomposition,different threads may score for the same tally accumulator.If the same memory location is updated simultaneously by more than two threads,it will lead to competition between threads known as thread race which is shown in Fig.4a.Thus,to prevent the error caused by the thread race,scoring operations must be protected by a thread lock.However,the thread lock operation is extremely time consuming,since all other threads are blocked once a thread acquires a thread lock.

To avoid this time consumption caused by the thread lock,a lockless concurrency method is introduced for memory access,wherein each thread is only allowed to accumulate the tally scores assigned to it.For example,Fig.4b shows that tally 1 calculated by thread 2 will be sent to thread 1 using MPI communication like Sect.2.2,instead of being directly accumulated by thread 2.This ensures that different threads do not update the same memory region simultaneously thereby eliminating the thread lock.

3 Results and discussion

Performance of the proposed method was tested using a PWR burnup assembly model,and its capability of handling a high- fidelity reactor wasveri fied using the BEAVRS model.The tests were performed on supercomputer nodes,each node comprising of 20 cores and 64 GB memory.Sixteen such nodes were used.

3.1 Pin cell model

Like any other code,a veri fication process is necessary for SuperMC as well.In our test,a pin cell benchmark exercise,described by Xu[17],was utilized to test the validity of SuperMC.The results of MCODE and CASMO techniques were taken directly from Xu[17].The main features of SuperMC,MCODE,and CASMO-4 are listed and compared in Table 1.An eigenvalue comparison is shown in Fig.5,and a comparison between methods with different isotope compositions is listed in Table 2.

Fig.3(Color online)Tally communication:a coarse-grained positioning communication,b fine-grained positioning communication

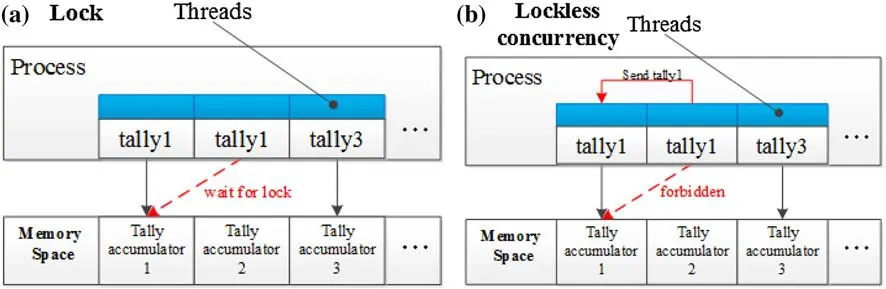
Fig.4(Color online)Diagram of tally accumulation:a memory access:lock,b memory access:lockless

Table 1 Main features of different burnup computational tools

Figure 5 shows the comparison between eigenvalue histories of SuperMC,CASMO-4,and MCODE.It can be seen from the figure that there exists a nearly constant k-inf difference between SuperMC and CASMO-4.It then grows as an approximately linear function.At a burnup of 100 MWd/kg,the difference in eigenvalues was observed to be about 0.0119.In addition to eigenvalue comparison,an isotope composition comparison at 100 MWd/kg is listed in Table 2.Most material compositions agreed well with CASMO-4 within typical uncertainties.This veri fied the transport–burnup capacity of SuperMC.

3.2 PWR assembly

The PWR burnup assembly model[18]contains 264 fuel pins with235U enrichment of 3.1%and 25 guide tubes.Each fuel pin is divided into 50 layers axially for burnup calculations with about 13,000 burnup areas,as shown in Fig.6(Color online).

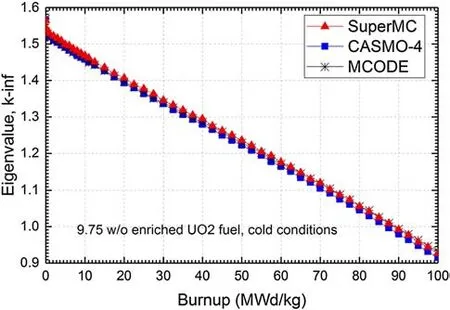
Fig.5(Color online)Eigenvalue comparison between SuperMC,CASMO-4,and MCODE

The assembly is depleted for 1 year with constant power,and the simulation process is separated into five equal time steps.The total simulated particle history of different threads is kept constant(weak scaling).Each thread employed 200 generations with 1000 neutron histories per generation,and the first 50 generations were discarded.

The performance of the thread-level data decomposition method was evaluated through three tests.First,performance of the lockless concurrency memory access pattern was evaluated and compared to that of the locked pattern.Figure 7a shows that the computing time of the lock pattern is almost 10 times that of the lockless pattern thereby indicating that the latter can effectively reduce contention for shared resources.Next,performance of the fine-grained positioning mode was evaluated and compared to that of the coarse-grained positioning mode.Figure 7b illustrates that the coarse-grained positioning communication time is almost twice that of the fine-grained positioning communication,which proves that the introduced fine-grained positioning communication mode offers great advantages in data transfer.Finally,the performance of thread-level data decomposition was compared to that of process-level data decomposition.For the PWR model,using tally datadecomposition method,majority of the material and nuclear cross-section data accounted for 1 GB of memory for each process,which corresponds to 20 GB memory for each node with 20 processes.However,with the threadlevel data decomposition method,the material and nuclear cross-section data occupied approximately 1 GB of memory for each process with 10 threads thereby accounting for 2 GB of memory for each node with two processes.Meanwhile,both methods required 2 GB of memory for tally data per node.Figure 7c shows that the memory consumption ofthe thread-leveldata decomposition method is almost 10 times compared to the process-level data decomposition method.The factor by which the memory consumption is reduced is close to the number of threads in each process.This shows that the developed method could effectively reduce memory consumption and substantially avoid data redundancy in a single process.

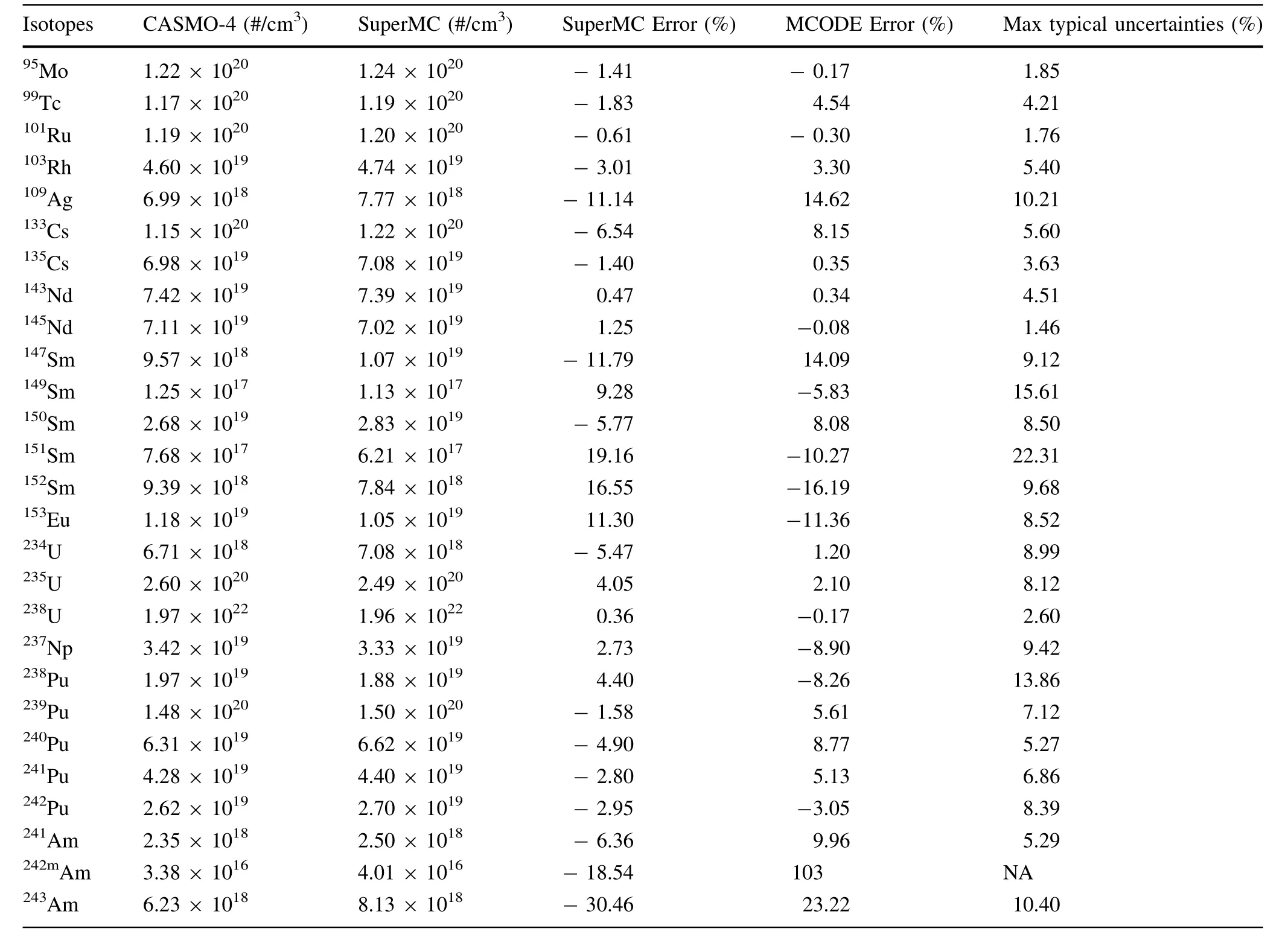
Table 2 Fractional difference between SuperMC,CASMO-4,and MCODE in nuclide concentration at 100 MWd/kg

Fig.6(Color online)PWR assembly model

3.3 BEAVRS model

In 2003,Massachusetts Institute of Technology(MIT)released its BEAVRS model based on a commercial reactor that includes detailed speci fications and measured data of a hot zero power condition and two cycles.The model consists of 193 fuel assemblies with a 17×17 pin arrangement and three235U enrichments of 1.6,2.4,and 3.1%[19].

Fig.8(Color online)Parallel performance and memory consumption for BEAVRS benchmark(10 threads were used per process)

The full-core transport–burnup calculation was performed with the thread-level data decomposition method.The number of burnup areas amounted to 1 million,which is unacceptable for any common parallel computing method.A series of tests were performed using strong scaling with the same amount of work across all threads.In the calculations,10 million particles were simulated per cycle.Each burnup step comprised of 150 inactive cycles and 850 active cycles.There were three such burnup steps.

The parallel performance is shown in Fig.8.This figure shows that as the number of threads increased,the parallel ef ficiency was maintained high,and the memory consumption at each node was rapidly reduced.

In addition,the transport–burnup calculation results were compared to the measured data,and the235U fission rate given by the burnup calculation on day 81 is shown in Fig.9.Each box represents a fuel assembly.Three numerical values are presented, which include experimental and SuperMC calculation results,as well as the difference between the two results.This finding shows that most of the differences are within 5%of one another,which is smaller than that obtained by Kelly[20].

Fig.9(Color online)Comparison of235U fission rate distribution on day 81

4 Conclusion

This work developed and implemented the thread-level data decomposition method,wherein the tally accumulators are decomposed to threads,while residual memory is shared in a single process.Lockless concurrency pattern and fine-grained positioning mode are used in this method to reduce contention for shared hardware resources.The performance and capacity of the developed method was tested using the typical PWR burnup assembly and BEAVRS model.It was demonstrated that the method could meet the memory demand of a full-core high- fidelity transport–burnup calculation and yet maintain high parallel ef ficiency.

AcknowledgementsThe authors would like to show their great appreciation to other members of the FDS team for extending their support to this research.

1.N.Horelik,B.Herman,B.Forget et al.,Benchmark for evaluation and validation of reactor simulations(BEAVRS),in InternationalConference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering(M&C2013),Sun Valley,USA,5–9 May 2013

2.K.Smith,B.Forget,Challenges in the development of highif delity LWR core neutronics tools,in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering(M&C2013),Sun Valley,USA,5–9 May 2013

3.P.K.Romano,B.Forget,The OpenMC Monte Carlo particle transport code.Ann.Nucl.Energy 51,274–281(2013).https://doi.org/10.1016/j.anucene.2012.06.040

4.G.Li,Study and application of parallel geometric region decomposition parallel algorithm for Monte Carlo particle transport.Ph.D.Thesis,China Academy of Engineering Physics,2014

5.P.K.Romano,A.R.Siegel,B.Forget et al.,Data decomposition of Monte Carlo particle transport simulations via tally servers.J.Comput.Phys.252,20–36(2013).https://doi.org/10.1016/j.jcp.2013.06.011

6.P.K.Romano,B.Forget,K.Smith et al.,On the use of tally servers in Monte Carlo simulations of light-water reactors,in International Conference Mathematics and Computation,Supercomputing in Nuclear Applications and the Monte Carlo Method(SNA+MC2013),Paris,France,27–31 Oct 2013

7.J.G.Liang,research on data parallel methods for large-scale calculations with reactor Monte Carlo Code RMC.Ph.D.Thesis,Tsinghua University,2015

8.C.M.Luo,S.Q.Tian,K.Wang et al.,Parallelizing AT with open multi-processing and MPI.Nucl.Sci.Tech.26(3),030104(2015).https://doi.org/10.13538/j.1001-8042/nst.26.030104

9.P.David,R.Brian,P.Dobreff et al.,Strategies and algorithms for hybrid shared-memory/message-passing parallelism in Monte Carlo radiation transport code,in International Conference Mathematics and Computation,Supercomputing in Nuclear Applications and the Monte Carlo Method(SNA+MC2015),Nashville,USA,19–23 Apr 2015

10.Y.Wu,J.Song,H.Zheng et al.,CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC.Ann.Nucl.Energy 82,161–168(2015).https://doi.org/10.1016/j.anu cene.2014.08.058

11.Y.Wu,F.D.S.Team,CAD-based interface programs for fusion neutron transport simulation.Fusion Eng.Des.84(7),1987–1992(2009).https://doi.org/10.1016/j.fusengdes.2008.12.041

12.Y.Wu,Z.Chen,L.Hu et al.,Identi fication of safety gaps for fusion demonstration reactors.Nat.Energy 1,16154(2016).https://doi.org/10.1038/nenergy.2016.154

13.Y.Wu,J.Jiang,M.Wang et al.,A fusion-driven subcritical system concept based on viable technologies.Nucl.Fusion 51,103036(2011).https://doi.org/10.1088/0029-5515/51/10/103036

14.Y.Wu,F.D.S.Team,Design analysis of the china dual-functional lithium lead(DFLL)test blanket module in ITER.Fusion Eng.Des.82,1893–1903(2007).https://doi.org/10.1016/j.fusengdes.2007.08.012

15.Message Passing Interface Forum,MPI:a message-passing interface standard.Version 3.0.http://mpi-forum.org/docs/mpi-3.0/mpi30-report.pdf

16.B.Chapman,G.Jost,R.Van Der Pas,Using OpenMP:Portable Shared Memory Parallel Programming(MIT press,Cambridge,2008)

17.Z.Xu,Design Strategies for Optimizing High Burnup Fuel in Pressurized Water Reactors.Ph.D.Thesis,Massachusetts Institute of Technology,2013

18.M.D.DeHart,C.V.Parks,M.C.Brady,OECD/NEA burnup credit calculational criticality benchmark phase IB results.Oak Ridge National Laboratory USA,ORNL-6901,1996

19.J.Leppa¨nen,R.Mattila,Validation of the Serpent-ARES code sequence using the MIT BEAVRS benchmark–HFP conditions and fuel cycle 1 simulations.Ann.Nucl.Energy 96,324–331(2016).https://doi.org/10.1016/j.anucene.2016.06.014

20.D.J.Kelly,B.N.Aviles,P.K.Romano et al.,Analysis of Select BEAVRS PWR Benchmark Cycle 1 Results Using MC21 And OpenMC.in The Physics of Reactors Conference(PHYSOR2014),Kyoto,Japan,Sept 28–Oct 3 2015