Energy distributions of multiple backscattered photons in materials

Asuman Aydın

1 Introduction

Radiation–matter interaction studies have increased rapidly in various fields such as nuclear and radiation physics,industrial,medical,engineering,and environmental applications.Theoretical and experimental studies on the interaction of gamma radiation with matter are of signi ficantimportance,especially to understand the mechanism of the detection and slowing down of gamma photons in applications of nuclear physics [1–9].Backscattering of gamma rays is a problem of fundamental importance in radiation shielding,dosimetry,and non-destructive testing of samples.Such studies have been conducted by several authors[10,11].

In Compton scattering experiments,the incident photon undergoes a number of scatterings within a thick material before it exits.These multiple scatterings of photons act as a background in Compton scattering studies.The energy distribution in a multiply scattered spectrum is much broader than that of a singly scattered one.An analogue MonteCarlo codewasdeveloped to simulatethe backscattering ofphotonsin materialswith various incoming energies.In this work,systematical calculations of energy distributions and backscattered probabilities for different media with various thicknesses of materials and energy ranges were performed using the Monte Carlo code.The simulation technique is based mainly on Compton scattering.This work aimed to obtain the energy distribution of multiply backscattered events followed by the interactions of photons with thick targets,using the Monte Carlo simulation.The distributions of backscattered photons after several scatterings in the materials are useful for applications in radiation shielding.

2 Theoretical methods

In this work,the photoelectric absorption and Compton scattering(incoherent)cross sections of gamma photons were acquired from XCOM database developed by Berger et al.[12].A continuous expression for the attenuation coef ficients(μ = μpho+ μcom)was obtained in the range 10 keV–5 MeV and expressed as a simple power expansion of the form

The fittings werecarriedout using the logarithm ofT(energy),and μ points and piare the parameters of photoelectric and incoherent attenuation coef ficients for each material.An exampleofthis fittingisshowninFig.1forboneasabiological material.The photoelectric interaction attenuation coef ficients have two different values that correspond to K and L atomic energylevelsoftheconstitutingatoms.Thesediscontinuitiesin the energy levels of atoms were taken into account for fitting.

We used Ozmutlu’s sampling algorithm[13]based on the acceptance–rejection method with an envelope rejection function for sampling the angular distribution in Compton scattering from Klein–Nishina differential scattering cross section[14–17].

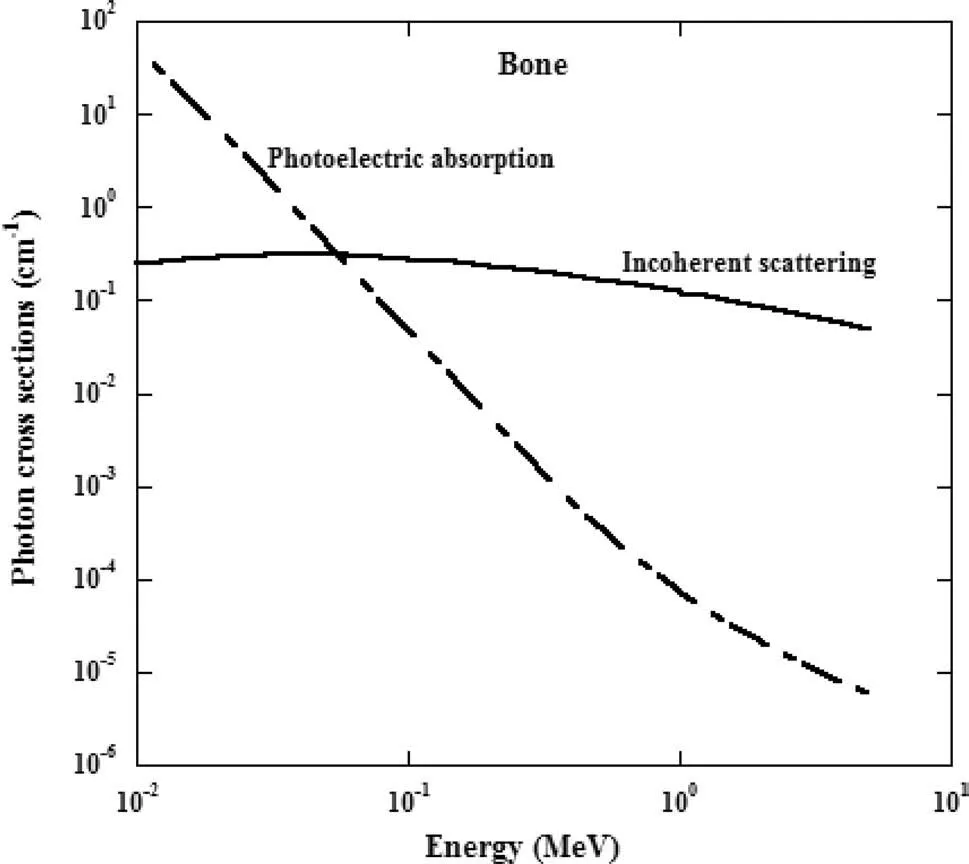
Fig.1 Attenuation coef ficients as a function of photon energies for bone material

In this work,a Monte Carlo code was written to provide insight into gamma ray backscattering,and simulation results for the energy distributions and the backscattered probabilities of gamma photons with various energies multiply backscattered from various targets are presented.As is usual for detailed Monte Carlo calculations,a gamma photon is represented by its energy,position coordinate（θ，Ø）,and direction cosines relative to some frame of reference.These quantities are chosen as randomly generated parameters with the selection of the processes(one of photoelectric or Compton)when an interaction occurs.The algorithm provides the energy distribution of backscattered photons after several scatterings in the materials.Materials such as lead,concrete,and water were chosen as scatterers due to the increasing interest in radiation dosimetry,radiation shielding,and detection,and slowing down of gamma photons.The results were obtained using two different geometries of the material:in finite and slab geometries.The slab geometry used in the simulations is as shown in Fig.2.

They were tracked within the material until they backscattered or slowed down below 10 keV.Typically,tens of thousands of photon trajectories need to be tracked to produce a statistically reasonable backscattering rate for a given incident energy.The time required to compute the multiple trajectories heavily depends on the initial energy of photons and targeted materials.

Fig.2 Scheme of multiple scattering in a material for slab geometry

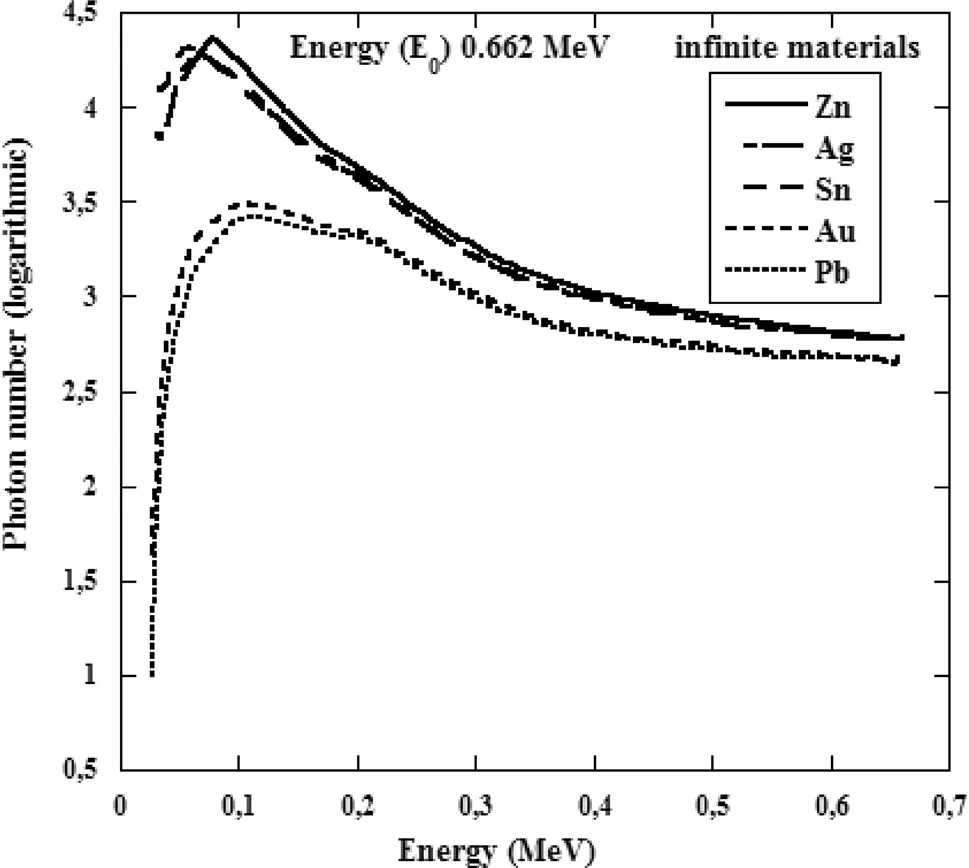
Fig.3 Energy distributions of multiple Compton scattering in in finite metallic materials

Fig.4 Energy distributions of backscattered photons in 20 cm thickness for Zn,Ag,Sn,and Au at 1.25 and 2.1 MeV

Fig.5 Energy distributions of backscattered photons in water,bone,and concrete at 0.279 MeV energy

3 Results and discussion

Monte Carlo simulations of the energy distribution of photons for elemental solids and biological and shielding materials were reported for the incident mono-energetic photon beams of 0.279,0.662,1.250,and 2.100 MeV.The energy distributions of backscattered photons for various thicknesses of aluminum,copper,zinc,silver,tin,gold,lead,water,bone,and concrete materials were calculated.

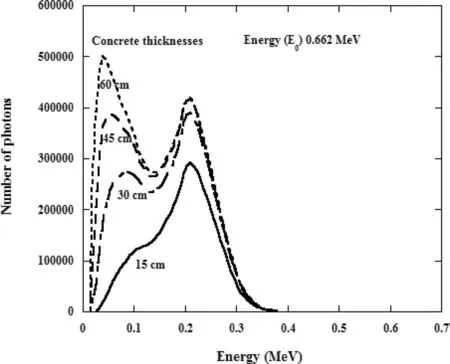
Fig.6 Dependence of backscattered energy distribution on concrete thicknesses at 0.662 MeV the photon energy

Fig.7 Comparison of energy distributions of backscattered photons for 0.279 and 0.662 MeV energies in concrete

For in finite material geometry,the multiple scattered photons are calculated for the energy distributions,which are found to be very similar to each other for different energies and materials.For all materials,the energy distributions initially increase and reach a maximum value;thereafter,they decrease rapidly with increasing photon energy.Since the energy distributions occur in a small energy region,a semi-logarithmic graph is drawn.Figure 3 shows the energy distributions of multiple scattered photons for elemental solids with in finite geometries at 0.662 MeV.

Fig.8 Energy distributions of backscattered photons in a lead,concrete,and water;and b water,muscle,and bone for 0.662 MeV(Akar et al.’s work compared to work carried out in the present study)

The backscattering energy distributions of gamma photons were calculated for different materials and incident photon energy with slab geometry.The mechanism of interaction depends on the type of particle,energy,and density and,especially,the number of protons in the medium.The results are shown in Fig.4 for zinc,silver,tin,and gold metallic materials with a constant thickness of 20 cm.The backscattering energy distributions show similar course for zinc,silver,and tin.They have two clear peaks at the same energy values of 0.05 and 0.25 MeV.It is considerable that the energy distributions of photons scattered backward from the various materials show peaks at approximately 0.25 MeV in the working energy range.We can call this a sudden jumping peak,and it is caused by only one Compton scattering in the material.On the other hand,the first peak is seen as a shoulder for gold.The second maximum of the backscattering energy distributions occurs at a different energy value compared to the other materials,probably due to a larger number of protons in gold.The inset of Fig.4 shows the backscattering energy distributions for the same materials at a constant thickness for 2.1 MeV energy of incident gamma photon.The backscattering energy distributions exhibit nearly the same behavior for these incident energies.Over 0.5 MeV,they go to almost zero for all materials as shown in the Fig.4.These results indicated that the backscattering energy distributions weaken as the medium atomic number increases due to Compton interactions.In other words,at the same energy value,as the atomic number of the medium increases,the number of backscattered photons decreases due to an increase in the photoelectric interaction cross sections.

Fig.9 Backscattering probability versus the thickness for aluminum and gold materials

The backscattering energy distributions of the gamma photons were calculated for biological and shielding materials.The results are shown in Fig.5 for bone,water,and concrete,where bone and water are selected as biological materials and concrete as a shielding material.The thicknesses of these materials are fixed at 35 cm and targeted with incident gamma photons of 0.279 MeV.

The variation ofmultiply scattered eventsunder backscattered energy peak as a function of target thickness of the concrete medium is shown in Fig.6 for 0.662 MeV energy.The energy distributions of backscattering gamma rays vary depending on the decrease in their probability of going forward as the thickness increases.As the thickness of the concrete increases,the first peak increases more rapidly compared to the second peak.In addition,the energy position of the first peak shifts toward the low energy value.On the other hand,the second peak position remains unchanged.

The backscattered energy distribution of concrete medium at a fixed thickness for two gamma photons with different energies is shown in Fig.7.The peak positions of the backscattered photons are shifted to higher energies as the incident photon energy increases.Although the peak intensity of the second peak remains nearly constant,the intensity of the first peak increases for higher photon energies.

There are only a few reports presented in literature on the study of energy distributions of multiple backscattered photons in materials with the same geometry,as investigated in this work[18,19].Akar et al.work followed the gamma photons with 0.662 MeV,the incident energy in biological and shielding materials with the thickness of five mean-free paths using the Monte Carlo method.The energy distributions of the backscattered photons acquired from Ref.[18]are shown in Fig.8a,b with our results for comparison for the same media,thicknesses,and energies.The simulation results were found to be in good agreement.The sudden jumping peaks appearing because of the single Compton scattering are also noted in Fig.8.

The experimental and theoretical studies in the literature[20–24]concerning the energy distribution of photons that reach the detector system after several successive Compton scatterings in the target observed similar trends in the relevant energy spectrums.

The backscattering intensity and energy probabilities are calculated for the backscattered gamma photons from different materials with various thicknesses.Typically,results are obtained for metallic,biological,and shielding materials.Figure 9 shows the calculated backscattering probabilities for photons entering into aluminum and gold materials as a function of thickness.The number of backscattered photons decreases with increasing density of the medium.In addition,the backscattering probabilities and energy rates(the ratio of the backscattered energy to the total incident photon energy as a percentage)remained almost constant for each material with a certain value of thickness.In other words,after a particular thickness,called saturation thickness,multiple backscattered photons are nearly constant in the target material.

4 Conclusion

In this research,we present a simple and considerably successful model based on the Monte Carlo simulation for the description of scattering events and penetration pro file of gamma photons in metallic,biological,and shielding materials for energies ranging a few hundreds of keV.The scattering processes include only Compton scattering.We observed an increase in the multiple backscattered photons with an increase in the target thickness.After a particular thickness,called saturation thickness,the number of multiple backscattered photons becomes nearly constant in the target material.

In all energy distributions,with the increase in the material density,the number of backscattered photons with low energies decreases.Therefore,the photoelectric effect is the dominant photon interaction process in the lower energy region.Additionally,this process depends heavily on the physical properties of the interacting material.

The results were compared with other theoretical data for different photon energies.It was realized that this simple Monte Carlo approach can be applied to the theoretical backscattering description of gamma photons.It can also be used ef ficiently to simulate the experimental conditions in nuclear applications.The energy distributions of transmitted photons from metallic,biological,and shielding materials with various thicknesses are under investigation.

1.T.Pitkanen,The multiple scattering pro file in gamma ray Compton studies.Nucl.Instrum.Methods Phys.Res.A 251,536–544(1986).https://doi.org/10.1016/0168-9002(86)90649-2

2.G.Nelson,D.Reilly,Gamma-ray interactions with matter.Passive Nondestruct.Anal.Nucl.Mater.NUREG/CR-5550,LA-UR-90-732,27–42(1991)

3.D.S.Vlachos,T.E.Simos,PDSW:a program for the calculation of photon energy distribution resulting from radioactive elements in seawater.Comput.Phys.Commun.174,391–395(2006).https://doi.org/10.1016/j.cpc.2005.10.010

4.P.P.Kane,Inelastic scattering of X-rays and gamma rays.Radiat.Phys.Chem.75,2195–2205(2006).https://doi.org/10.1016/j.radphyschem.2006.08.001

5.B.K.Chatterjeea,L.A.LaJohnb,S.C.Roy,Investigations on Compton scattering:new directions.Radiat.Phys.Chem.75,2165–2173(2006).https://doi.org/10.1016/j.radphyschem.2006.03.073

6.F.Gao,Gamma-ray interaction in Ge:a Monte Carlo simulation.Nucl.Instrum.Methods Phys.Res.B255,286–290(2007).https://doi.org/10.1016/j.nimb.2006.11.031

7.M.Singh,G.Singh,B.S.Sandhu et al.,Energy and intensity distributions of 0.279 MeV multiply Compton-scattered photons in soldering material.Nucl.Instrum.Methods Phys.Res.A 580,54–57(2007).https://doi.org/10.1016/j.nima.2007.05.016

8.S.Pomme,Detection ef ficiency calculation for photons,electrons and positrons in a well detector.Part I:analytical model.Nucl.Instrum.Methods Phys.Res.A 604,584–591(2009).https://doi.org/10.1016/j.nima.2009.03.076

9.F.Salvat,J.M.Ferna´ndez-Varea,Overview of physical interaction models for photon and electron transport used in Monte Carlo codes.Metrologia 46(2),S112–S138(2009).https://doi.org/10.1088/0026-1394/46/2/S08

10.A.D.Sabharwal,B.Singh,B.S.Sandhu,Investigations of multiple backscattering and albedos of 1.12 MeV gamma photons in elements and alloys.Nucl.Instrum.Methods Phys.Res.Sect.B 267,151–156(2009).https://doi.org/10.1016/j.nimb.2008.10.072

11.S.M.T.Hoang,S.Yoo,G.M.Sun,Experimental validation of the backscattering gamma-ray spectra with the Monte Carlo code.Nucl.Eng.Technol.43(1),13–18(2011).https://doi.org/10.5516/NET.2011.43.1.013

12.M.J.Berger,J.H.Hubbell,S.M.Seltzer,et al.,XCOM:photon cross sections database(2010),http://www.nist.gov/pml/data/xcom/index.cfm/

13.E.N.Ozmutlu,Sampling of angular distribution in Compton scattering.Appl.Radiat.Isot.43(6),713–715(1992)

14.O.Klein,Y.Nishina,U¨ber die Streuung von Strahlung durch freie Elektronen nach der neuen relativistischen Quantendynamik von Dira.Z.Phys.52(11–12),853–869(1929)

15.D.V.Rao,R.Cesareo,G.E.Gigante,Elastic and Compton scattering cross sections in the atomic regions 12≤Z≤82.Appl.Radiat.Isot.47(2),219–227(1996).https://doi.org/10.1016/0969-8043(95)00270-7

16.P.M.Bergstrom,R.H.Pratt,An overview of the theories used in Compton scattering calculations.Radiat.Phys.Chem.50(1),3–29(1997).https://doi.org/10.1016/S0969-806X(97)00022-4

17.R.H.Pratt,L.A.Lajohn,V.Florescu et al.,Compton scattering revisited.Radiat.Phys.Chem.79,124–131(2010).https://doi.org/10.1016/j.radphyschem.2009.04.035

18.U.A.Tarım,O.Gurler,E.N.Ozmutlu et al.,Monte Carlo calculations of the energy deposited in biological samples and shielding materials.Radiat.Eff.Def.Solids 169(3),232–238(2014).https://doi.org/10.1080/10420150.2013.841161

19.Y.R.Icin,Investigation of gamma backscattering in various media using Monte Carlo method.Master of Science Thesis,Balikesir University,Institute of Science,Physics Balikesir,Turkey(2016)

20.R.K.Swami,K.U.Kiran,K.M.Eshwarappa et al.,Experimental investigation of multiply backscattered gamma photons in metals,glass and granites and their saturation thickness.Int.J.Sci.Res.1(4),255–261(2013)

21.U.A.Tarım,O.Gurler,E.N.Ozmutlu et al.,Monte Carlo analyses of multiple backscattering of gamma photons.J.Radioanal.Nucl.Chem.295,901–905(2013).https://doi.org/10.1007/s10967-012-2206-z

22.A.D.Sabharwal,B.S.Sandhu,B.Singh,Investigations of energy dependence of saturation thickness of multiply backscattered gamma photons in elements and alloys—an inverse matrix approach.J.Phys.Conf.Ser.312,1–6(2011).https://doi.org/10.1088/1742-6596/312/5/052021

23.A.D.Sabharwal,B.S.Sandhu,B.Singh,Investigations of effect of target thickness and detector collimation on 662 keV multiply backscattered gamma photons.Radiat.Meas.44(4),411–414(2009).https://doi.org/10.1016/j.rad.meas.2009.06.010

24.M.Singh,G.Singh,B.Singh et al.,Experimental observation of energy dependence of saturation thickness of multiply scattered gamma photons.Radiat.Phys.Chem.77,991–995(2008).https://doi.org/10.1016/j.radphyschem.2008.06.003