A modi fied multi-group model of angular and momentum distribution of cosmic ray muons for thickness measurement and material discrimination of slabs

Sa Xiao•Wei-Bo He•Ming-Cong Lan•Ying Chen•Mao-Bing Shuai,2

1 Introduction

The abundant cosmic ray muons generated in the atmosphere have provided a natural tomographic probe capable of penetrating the great thickness of uranium and lower Z materials[1–6].Since the imaging from the scattering of cosmic ray muons,known as muon tomography(MT),was developed by Los Alamos National Laboratory(LANL)in 2003[2,3],this technique has been widely used to explore the density and geometry of objects sealed in a well-designed shielding or exposed in a background of clutter[7].It facilitates the detection of potential nuclear threats hidden in the cross-border transportation without informing the drivers and passengers and has been commercialized by LANL and Decision Science Corp.for security check at US ports[8–12].

Muon tomography uses Coulomb scattering information between muons and the traversed materials to produce 3D images of high-Z objects.In this technique,a huge number of incoming and outgoing muon trajectories acquired by a group of speci fic detectors were employed to reconstruct the material composition of target objects on the basis of the Moliere equation,which empirically describes the relationship between the overall scattered angle and the path length.Therefore,the algorithm used for image reconstruction is of great importance.However,according to the Moliere equation,muons with different zenith angles and momenta will suffer distinctive Coulomb scattering even in the same object.Previous algorithms[4],such as PoCA and MLSD,usually obscured this difference by making an approximation that all the involved muons were regarded as the same in momentum(typically 3 GeV/c,the mean momentum of muons)and that the deviation in zenith angle(ZA)was ignored.Although having been applied successfully in a number of scenarios,the 3 GeV approximation could become too coarse for higher resolution requirements.For a speci fic momentum of incident muons,an empirical formula(Moliere equation)describes the relationship between the overall scattered angle and the properties of the object.However,the variability of cosmic ray muons in momentum and incident angle complicates their scattering behaviors in the object making it dif ficult to describe them precisely by some explicit equations.Therefore,the 3 GeV approximation should be thought over and renewed by a better one.

In this paper,we report a modi fied multi-group(MMG)model regarding the momentum spectra and angular distribution of cosmic ray muons,by adjusting the original multi-group(MG)model proposed by Morris[13].With the help of the renewed model,a more precise relationship between the muon scattering and the properties of the traversed object is obtained for slab targets.This model is then validated by testing its performance in two scenarios.It works well both in measuring the thickness of a Pb slab and in identifying the material of which a slab consists,even in the matter of incomplete angular data.Moreover,once this novel model is to be applied to objects other than slabs and properly integrated into present algorithms for image reconstruction,a considerable improvement can be expected in the quality and ef ficiency of muon tomography.

2 Methodology

2.1 Principle of muon tomography

A cosmic ray muon undergoes a random walk in the traversed material due to the multiple Coulomb scattering with atomic nuclei,resulting in an outgoing path de flected by a scattering polar angle.Empirically,the statistical relationship between the scattering angle distribution of abundant muons and the properties of the traversed materials can be described as following,which is known as the Moliere equation[14,15]:

whereθ isthescatteringangle,Nisthenumberofmuons,f（·）is the probabilistic density function,and σ,the mean square root(RMS)of θ,is given by Fermi approximation[16]:

where p is the particle momentum in MeV/c,β is its velocity,l is the path length,and X0is the radiation length(RL)of the material,which drops rapidly with atomic number,Z.For a path length of 10 cm,a 3 GeV/c muon will scatter 2.3 milliradians in water(X0=36 cm)on the average,11 milliradians in iron(X0=1·76 cm),or 20 milliradians in lead(X0=0·56 cm).If the scattering angle in an object is measured and the particle momentum is well known,then the path length can be calculated.Nevertheless,it is unpractical to obtain the momentum of every single muon using existing MT instruments.An alternative solution to the problem is required.

2.2 The modi fied multi-group model

2.2.1 Momentum consideration

Since the cosmic ray muons differ widely in momentum,from a few MeV/c to hundreds of GeV/c,the scattering features may vary from each other.For example,muons with a momenta of 0.3 GeV/c would be scattered by a de flection angle of 10 mrad in a Pb slab of 10 cm,while those with momenta of 3 GeV/c would only be scattered by 0.5 mrad,apparently smaller than the former.Therefore,the effects of momentum should be fully considered.Other than the original MG model[13],where seven momentum groups were used,but the higher portion of muon momenta was not precisely modeled,we have approximated the scattering distribution as a summation over nine momentum groups ranging from 0.25 to 64 GeV/c:

where ciis the amplitude of the ith group.By convolving Eqs.3 with 1,the scattering distribution can be described more precisely as:

where Aiand σiare the weighing factor and RMS scattering angle for the ith group,respectively.Equations 5 and 6 build up a mathematical description of multi-group model regarding the momentum spectra of muons.

2.2.2 Angular modi fication

Regarding that the cosmic ray muons come from different directions,according to the angular distribution given by Bai[17],the path length for each muon must be a variable.For a slab target of thickness l,an incoming muon with a zenith angle of α will go through a path length of l/cosα in the target.Regarding this,an angular modi fication should be applied to the multi-group model for accurate calculations,by substituting σiwith

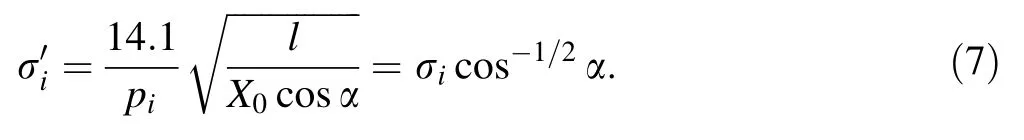
Therefore,there is a proportional relationship between the modi fiedand the original σi.The scattered angle of each muon with zenith angle,α,will be modi fied by multiplying a factor of cos1/2α to be an equivalence of that of muons with 0°zenith angle.By this modi fication to the original multi-group model,the zenith angle difference of cosmic ray muons was eliminated and all the path lengths of incident muons were converted to the same value,i.e.,the thickness l of the slab target.In the next section,the modi fied multi-group(MMG)model will be discussed with both complete and incomplete angular data.

3 Results and discussion

3.1 MMG model with complete angular data

3.1.1 GEANT4 simulation

We use the CRY Monte Carlo generator[18]to generate muons with angular distribution and momentum spectra corresponding to those of cosmic ray muons at sea level.The CRY generator is interfaced with the GEANT4 toolkit[19,20](version 10.2)for generating cosmic ray muons and simulating the MT system geometry and muon interactions.GEANT4 has proved to be a successful tool for simulating muon scatterings in a series of objects[3,21].A schematic of the GEANT4 model,including a sample of muon interaction with the slab,is illustrated in Fig.1.The sizes of the CRY plane and the detector planes are deliberately chosen to have much larger dimensions than the target so that cosmic ray muons with large zenith angles can be taken into account.In an independent run,the number of simulated muons was equivalent to 1000cm-2,comparative to an exposure time of～17 h at sea level.For simulating the muon interactions within the target material,we use the standard GEANT4 muon physics processesforionization,multiple scattering,Bremsstrahlung,and pair production with default settings for production thresholds of secondary particles.Since this study is focused on the multiple scattering of muons,the position resolution of the detectors in the MT system is assumed to be perfect.As well,the secondary particles produced in these interactions are not propagated any further and their in fluence on particle detection is neglected.The path of each primary muon is stepped through the entire detector volume by the simulation.

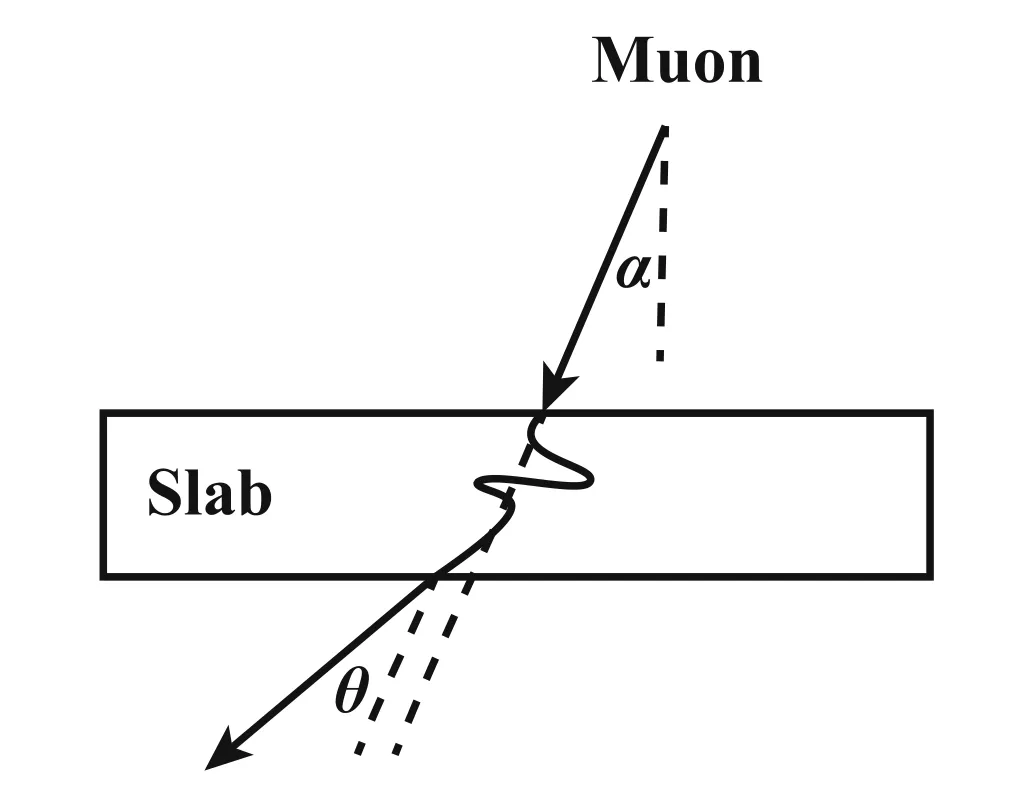
Fig.1 Schematic of the GEANT4 model,including a sample of muon interaction with the slab

3.1.2 Calibration of weighing factors

Several thicknesses(1.4,2.8,5.6,and 11.2 cm)of lead were simulated to calibrate the weighing factors.For each thickness,a one-dimensional histogram of scattering angle in 1 mrad steps from-100 to 100 mrad was created after a normalization that divided muon count in a single bin by the total number of muons,as shown in Fig.2(dots).Each histogram contained a convolution of the different muon momenta and the path lengths of lead.The data were then used to calibrate the MMG model.The weighing factor,Ai,of each momentum group,was fitted by a least squares fit of the MMG model to the data.This model did not account for changes in the shape of the muon spectrum due to stopping.Every single fit to the set of lead data was superimposed on the corresponding histogram in Fig.2(dashed lines).Also shown was the decomposition of each data set into its momentum groups(solid lines).The figure illustrated that the MMG model performed a precise fit(R2＞0·9995)to the simulated data.

3.2 MMG model with incomplete angular data

In a real-life application,MT measurements are always carried out acquiring muons limited within a small range of zenith angles,since not all of the cosmic ray muons are available due to the detector geometry.Therefore,the incompleteness of angular data should be accounted for.It was shown that the muons detected on a typical MT system are primarily concentrated in the zenith angle range from0°to 45°(93.4%)[17].If the range shrinks to 0°-24°,the muon percentage goes down to～48%.Regarding this,the two upper limits of the zenith angle,45°and 24°,were selected for incomplete data simulation.The simulation and MMG fits were done similarly to Sect.3.1 except that all the muons with a zenith angle out of the range were neglected.Results for zenith angle limits of 45°and 24°were shown in Figs.3 and 4,respectively.In spite of lack of large scattering data,the scattering data were well matched(R2＞0·9990)by MMG model for both limits.

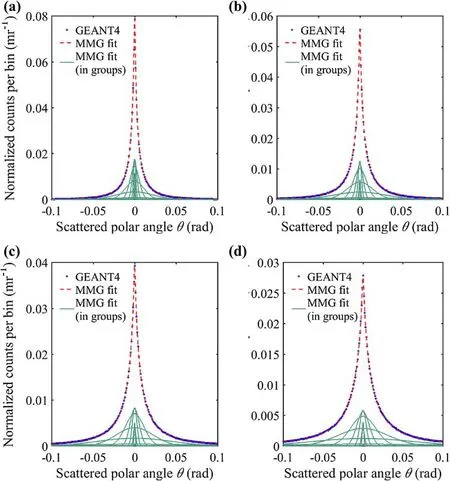
Fig.2(Color online)MMG model with complete angular data.a Pb thickness of 1.4 cm,b Pb thickness of 2.8 cm,c Pb thickness of 5.6 cm and d Pb thickness of 11.2 cm

4 Performance

This section shows the performance of the MMG model in two common scenarios.The first scenario of interest is that of a solitary Pb slab hidden in an empty box,in which the model needs to be able to identify the thickness of the slab.The second one is similar to the former,but the size of the slab is well known while the material composition is questioned.For either scenario,the performance of the MMG model is tested with both complete angular data and incomplete angular data(ZA＜45°or ZA＜24°).

4.1 Thickness evaluation of Pb slabs

This section shows the ability of the MMG model to evaluate the thickness of a Pb slab in an otherwise empty container.Let N0refer to the probabilistic density at θ=0 in the histograms above,then N0,in case of a precise fit,can be calculated as:

Then,both Eqs.6 and 8 were substituted to Eq.5,obtaining the estimated thicknessÎ of Pb slab:

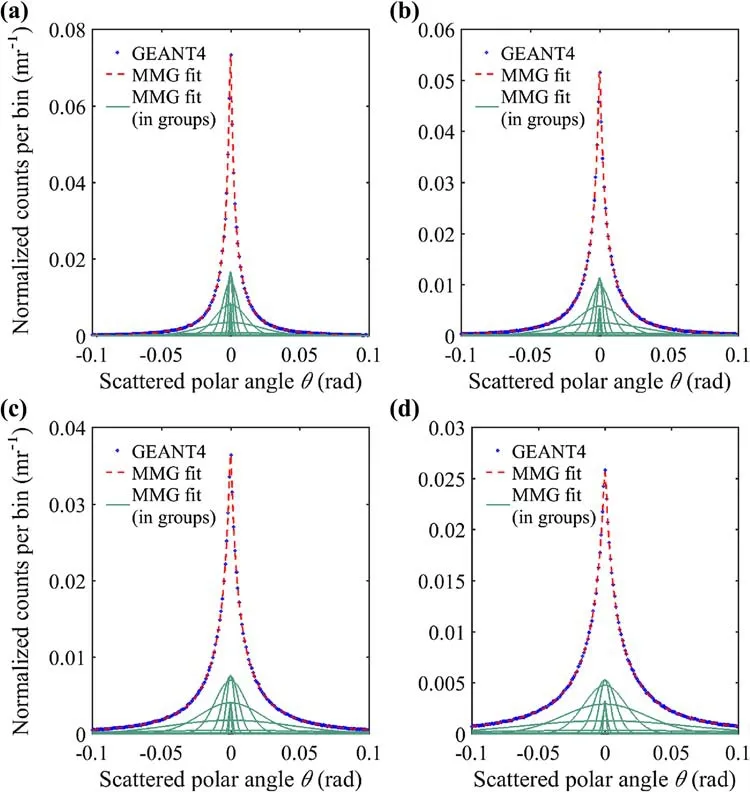
Fig.3(Color online)MMG model with incomplete angular data(ZA＜45°).a Pb thickness of 1.4 cm,b Pb thickness of 2.8 cm,c Pb thickness of 5.6 cm and d Pb thickness of 11.2 cm

Five Pb slabs with thicknesses ranging from 2 cm to 10 cm were selected for thickness evaluation by the MMG.The estimated results of each slab are shown in Table 1,in case of either complete or incomplete angular data(ZA＜45°or ZA＜24°).For comparison,results from the original MG are also listed in Table 1.The data were obtained from the mean of the 5 fits to the 5 independent runs.Although the complete ZA of incident muons were provided to both models,the MMG estimated the thicknesses overall more precisely than those obtained from MG,since the angular data were only taken into account in the former one.

Cases of incomplete angular data were expected to result mainly in somewhat reduced statistics,which may cause the evaluated results to deteriorate.However,minor discrepancies existed in the results from the three collections of angular data,which was probably due to the signi ficantly fewer muons with large scattering angles and the inferior tail effect in MMG fits.The three estimated thicknesses for each slab mostly agreed well with the reference data(within an error of 4%).A little exception was the cases where the thicknesses were 8 and 10 cm,in which deviations between the model fits and the reference data were relatively larger.We believe that the deviations were attributed to the nonlinearities introduced by the MMG model fits and its calibration of weighing factors.A better result should be expected if additional slabs were introduced for calibration of weighing factors.

4.2 Material identi fication of unknown slabs

This section illustrates the capacity of the MMG model to discriminate materials with different radiation lengths.The selected scenario is similar to that in Sect.4.1,but the slab with a fixed thickness of 2 cm is composed of unknown material.The material was selected from five candidates:concrete,iron,lead,tungsten,and uranium.The radiation lengths of the five candidates are listed in Table 2.The MMG model was used to identify the material of the slab by estimating the radiation length,^X0,as:

Fig.4(Color online)MMG model with incomplete angular data(ZA＜24°).a Pb thickness of 1.4 cm,b Pb thickness of 2.8 cm,c Pb thickness of 5.6 cm and d Pb thickness of 11.2 cm

Table 1 Estimated thicknesses of Pb slabs by MG and MMG

Table 2 Estimated radiation lengths of 2-cm slabs composed of unknown materials by MG and MMG

where N0can also be calculated by Eq.8.Results for all the five test objects are shown in Table 2,with both completeand incompleteangulardata(ZA＜45°or ZA＜24°).The corresponding MG results were also implemented for comparison.The data were obtained from the mean of the 5 fits to the 5 independent runs.Instead of the MG,the MMG gave out results much closer to the reference data for all the five materials with a complete ZA data of muons and therefore proved to be highly reliable and effective.Again,cases of complete and incomplete angular data provided comparative results for all of the test materials.Therefore,we can infer that our model is insensitive to the absence of large scattering data,so it is practical in real MT experiments.

Notice that our model provided more precise radiation lengths of lead and tungsten(both within an error of＜2%)thantheothermaterials.Sincetheweighingfactorsusedinthe MMG model were calibrated by lead,these remarkable consistencies were believed to be attributed to their similarity of lead and tungsten in the aspect of interactions with muons.

5 Conclusion

The implementation of the modi fied multi-group model in this paper enhances the capabilities of muon tomography,since it has taken into account the effects of the angular distribution and momentum spectra of cosmic ray muons.Performance tests have established that the MMG model is capable of measuring the thickness of a Pb slab and identifying the material of an unknown slab on a reasonable exposure timescale, making a noticeable improvement in preciseness to the original MG model as well.Furthermore,the MMG model was proved to be insensitive to the absence of large scattering data,which is practical in real MT measurements.Future work will be done to integrate the model into present imaging algorithms,which is probably helpful to improve the capability of threat detection in portal monitoring.

1.K.N.Borozdin,G.E.Hogan,C.Morris et al.,Surveillance:radiographic imaging with cosmic-ray muons.Nature 422(6929),277(2003).https://doi.org/10.1038/422277a

2.L.J.Schultz,K.N.Borozdin,J.J.Gomez et al.,Image reconstruction and material Z discrimination via cosmic ray muon radiography.Nucl.Instrum.Methods A 519,687–694(2004).https://doi.org/10.1016/j.nima.2003.11.035

3.W.C.Priedhorsky,K.N.Borozdin,G.E.Hogan et al.,Detection of high-Z objects using multiple scattering of cosmic ray muons.Rev.Sci.Instrum.74,4294–4297(2003).https://doi.org/10.1063/1.1606536

4.R.C.Hoch,Master thesis,Florida Institute of Technology(2009)

5.J.Perry,Ph.D.thesis,University of New Mexico(2013)

6.J.O.Perry,J.D.Bacon,K.N.Borozdin et al.,Analysis of the multigroup model for muon tomography based threat detection.J.Appl.Phys.115,064904(2014).https://doi.org/10.1063/1.4865169

7.J.Snuverink,The ATLAS Muon Spectrometer:Commissioning and Tracking(University of Twente,Enschede,2009)

8.M.Bandieramonte,V.A.Delogu,U.Becciani et al.,Automated objectrecognition and visualization techniquesformuon tomography data analysis,in 2013 IEEE International Conference on Technologies for Homeland Security(HST),Institute of Electrical and Electronics Engineers(IEEE)(2013).https://doi.org/10.1109/THS.2013.6699057

9.M.Furlan,A.Rigoni,S.Vanini et al.,Application of muon tomography to detect radioactive sources hidden in scrap metal containers.IEEE Trans.Nucl.Sci.61,2204–2209(2014).https://doi.org/10.1109/TNS.2014.2321116

10.R.Patnaik,Y.Lee,D.Dorroh,Image based object identi fication in muon tomography,in 2014 IEEE Nuclear Science Symposium and Medical Imaging Conference(NSS/MIC)(Institute of Electrical and Electronics Engineers(IEEE),2014).https://doi.org/10.1109/NSSMIC.2014.7431145

11.G.Blanpied,S.Kumar,D.Dorroh et al.,Material discrimination using scattering and stopping of cosmic ray muons and electrons:Differentiating heavier from lighter metals as well as low-atomic weight materials.Nucl.Instrum.Methods A 784,352–358(2015).https://doi.org/10.1016/j.nima.2014.11.027

12.M.Sossong,G.Blanpied,S.Kumar et al.,Cosmic ray generated charged particles for cargo inspection,in NATO Science for Peace and Security Series B:Physics and Biophysics,Nuclear Threats and Security Challenges(2015),pp.229–243.https://doi.org/10.1007/978-94-017-9894-5_21

13.C.L.Morris,K.Borozdin,J.Bacon et al.,Obtaining material identi fication with cosmic ray radiography.AIP Adv.2,042128(2012).https://doi.org/10.1063/1.4766179

14.C.T.Case,E.L.Battle,Molie`re’s theory of multiple scattering.Phys.Rev.169,201–204(1968).https://doi.org/10.1103/Phys Rev.169.201

15.W.T.Scott,The theory of small-angle multiple scattering of fast charged particles.Rev.Mod.Phys.35,231–313(1963).https://doi.org/10.1103/RevModPhys.35.231

16.C.L.Morris,J.Bacon,K.Borozdin et al.,A new method for imaging nuclear threats using cosmic ray muons.AIP Adv.3,082128(2013).https://doi.org/10.1063/1.4820349

17.C.Bai,S.Simon,J.Kindem et al.,Muon tomography imaging improvement using optimized limited angle data,Proceedings of SPIE 9073,Chemical,Biological,Radiological,Nuclear,and Explosives(CBRNE)Sensing XV,907318(2014).https://doi.org/10.1117/12.2049977

18.C.Hagmann,D.Lange,D.Wright,Cosmic-ray shower generator(CRY)for Monte Carlo transport codes,in IEEE Nuclear Science Symposium ConferenceRecord,vol.2007,no.2 (2007),pp.1143–1146.https://doi.org/10.1109/NSSMIC.2007.4437209

19.S.Agostinelli,J.Allison,K.Amako et al.,Geant4—a simulation toolkit.Nucl.Instrum.Methods A 506,250–303(2003).https://doi.org/10.1016/S0168-9002(03)01368-8

20.J.Allison,K.Amako,J.Apostolakis et al.,Geant4 developments and applications.IEEE Trans.Nucl.Sci.53,270–278(2006).https://doi.org/10.1109/TNS.2006.869826

21.D.Mitra,A.Banerjee,S.Waweru et al.,Simulation study of muon scattering for tomography reconstruction,in IEEE Nuclear Science Symposium Conference Record(NSS/MIC)(2009).https://doi.org/10.1109/NSSMIC.2009.5402209