Measurement of keffby delayed neutron multiplication in subcritical systems

Bin Ye•Chao-Wen Yang•Chun Zheng

1 Introduction

Subcriticality is an important concept for monitoring the safety of reactor operation in critical or near-critical states.The neutron source multiplication(NSM)method is widely used to acquire nuclear system reactivity in nuclear safety analysis[1–7].Experimental NSM investigations were carried out in several facilities worldwide in recent years,including the Kyoto University CriticalAssembly‘KUCA’facility[8–10],the YALINA thermal subcritical assembly[11,12],and the MASURCA reactor through the series of MUSE experiments of the fast subcritical mockup[13–15].These studies investigated the nuclear characteristics in NSM experiments and examined the neutron properties of subcritical systems.Neutrons involved in those experiments were 14 MeV pulsed neutrons,252Cf spontaneous fission neutrons,deuterium–deuterium(D–D),and deuterium–tritium(D–T)neutrons.Different neutron source distributions(distributed in space,energy,and angle)have different effects on the multiplication of the nuclear systems.

The NSM method is a simple measurement technique which may feasibly be carried out in real time.This method does not require any special equipment other than a stationary external neutron source and an ordinary neutron detector.Additionally,the NSM method is based on steady-state analysis,so that this technique is very suitable for real-time measurement.Despite these advantages,the absolute value of subcriticality cannot be measured directly by the NSM method.One of the important reasons is that extra neutron sources used in the NSM experiments are very different from eigen-distribution neutron source(fundamental-mode fission sources)in space,energy,and angle distribution.It is impossible for extra neutron sources to distribute uniformly throughout the system volume.When the neutron sources are eigen-distribution neutron sources,the effective multiplication factor keffcan be directly related to the neutron multiplication factor M by M=1/(1-keff).However,the fundamental-mode source is a fictitious source distribution that does not exist in reality.In order to establish the relationship between the ordinary neutron source and fundamental-mode source,Spriggs et al.[16]have developed the theory of equivalent fundamental-mode sources and demonstrated a factor that could convert any arbitrary source distribution to an equivalent fundamental-mode source distribution.They also demonstrated a method for calculating this factor in subcritical systems.In China,Du and Yin[17,18]developed the Monte Carlo analysis method to calculate the equivalent fundamental-mode source strength of 14 MeV neutrons and spontaneous fission neutron sources in CFBRII reactors,respectively.

Two neutron source distributions(distributed in space,energy,and angle)producing the same number of neutrons will not necessarily contribute equally toward the multiplication of the given system.For this reason,equally sized units added to the system will have different effects on the multiplication of the system.Fundamental-mode neutrons and delayed neutrons that are all produced from fission events in critical system should be identically distributed in space and angle,varying only in energy spectrum.Therefore,we could introduce a factor to convert delayed neutron distribution to an equivalent fundamental-mode source distribution,i.e.,introduce a factor to eliminate the energy distribution difference between eigen-distribution neutron sources and delayed neutron sources in the NSM experiments to acquire keffof the nuclear system.

In this paper,we build on the concept of equivalent fundamental-mode source to propose using delayed neutrons as an extra neutron source in NSM experiments to acquire keffof the subcritical system.The paper is structured to begin with a statement of basic theory;thereafter,our use of the Monte Carlo analysis method to calculate the equivalent fundamental-mode source strength of delayed neutrons is demonstrated;then,the multiplication experiments we conducted in subcritical systems using delayed neutrons as a driving source to measure keffare described;and finally,conclusions are drawn,and future work is outlined.

2 Delayed neutron multiplica tion

In this section,we describe a novel method to determine keffof subcritical system using delayed neutron multiplication.Delayed neutrons are born from fission events and spread all over the system.They can induce fission events and proliferate neutrons like other ordinary neutrons.Delayed neutron multiplication can be measured by an appropriate method.The determination of kefffrom delayed neutron multiplication is predicated based on an understanding of the concept of equivalent fundamental-mode source.

In a subcritical system,if the source S was distributed as a fundamental-mode fission source,the fundamental-mode multiplication,M0,would be related to the effective multiplication factor of the system,keff,as follows:

However,the equivalent fundamental-mode source is a fictitious theoretical source.In experiments,arbitrary sources that have been placed in or near the assembly(such as an external startup neutron source)will produce system multiplication,M,that can differ signi ficantly from the fundamental-mode multiplication,M0.

Because it is customary in reactor physics to express most quantities in terms of keff,it is necessary to modify Eq.(1)by including a factor g*that allows us to express the actual multiplication produced by an arbitrary source distribution in terms of the fundamental-mode multiplication.That is,

This factor g*can be de fined as the ratio of the fixedsource multiplication to the fundamental-mode multiplication and is used to relate a given source strength to its equivalent fundamental-mode source strength [16].Therefore,g*is multiplied by the source strength of the neutron source to yield a fundamental-mode source strength,Q,de fined as Q=g*S.Therefore,the product,g*S,represents the equivalent fundamental-mode source.

A method for determining keffby delayed neutron multiplication will now be described.Delayed neutrons need to be acquired first.To produce these,a nuclear device is operated in critical mode for a moment and delayed neutron precursors are produced.Delayed neutrons precursors distribute throughout the system,and then,the device is shut down to stop the fission events.Subsequently,the existent precursors in the system decay.At this point,only delayed neutrons exist in the system(and no more prompt neutrons).A few minutes later,the reactor enters a subcritical state from shutdown mode;thus,delayed neutron multiplication is realized.Then,keffof the system can be acquired according to the relationship between keffand delayed neutron multiplication(Mdn).The multiplication of delayed neutrons in every step above is now described.

While the reactor is running,delayed neutron precursors are all continuously being produced and decaying.Precursors release neutrons called delayed neutrons.When the reactor operates in critical mode for more than 10 min,precursors′generation and decay will reach dynamic equilibrium according to the characteristics of delayed neutron precursors.The neutron detectors count rate,n1,in the system should be:

where ε is the neutron detector ef ficiency,ν is the average yield of neutrons per prompt fission,α is the ratio of prompt neutrons capture to fission cross section,and˙F is the fission rate of reactor in critical mode(s-1),which can be calculated from the running power:˙F=P×3·1×1010.

When the density of delayed neutron precursors reaches saturation,the reactor is shut down.Fission events cease,and delayed neutron precursor production also ceases.The precursors that existed in the whole system subsequently decay.The decay properties of precursors determine that the shorter a precursor’s half-life,the faster it disappears.According to six groups of delayed neutron model,the 1-th precursor with the longest half-life(87Br:T1/2=55.6 s in ENDF/B-VI)has the slowest decay behavior.Thereafter,300 s after the fission events stop,only 1-th delayed neutrons exist in the system[19].The emission rate(which can be de fined as neutron source intensity)of the 1-th delayed neutrons at time t beginning from the shutdown moment,Sdn,can be given by

where t is the time,start from the reactor shutdown(s);T is the time duration while reactor run in critical mode(s);νdis the total yield of delayed neutron precursors per fission;a1is the relative abundance of 1-th delayed neutron precursor;λ is the radioactive decay constant of 1-th delayed neutron precursor(s-1);and Sdnis the delayed neutrons source intensity at time t(s-1).

If the time duration,T,that the system is kept at in a critical state is greater than ten half-lives of87Br,all the precursors could reach saturation,giving:1-e-λT≈ 1.Then,Eq.(5)should be

Alternatively,according to the theory of equivalent fundamental-mode source,1-th delayed neutrons fundamental-mode source strength(Qdn)could be written as

More than 300 s after the fission events stop,the reactor steps into a subcritical state,the relationship between multiplication(M),keff,the multiplication of the system,leakage of the neutrons and ef ficiency of the detector,and the neutron detector counting rate n2should be

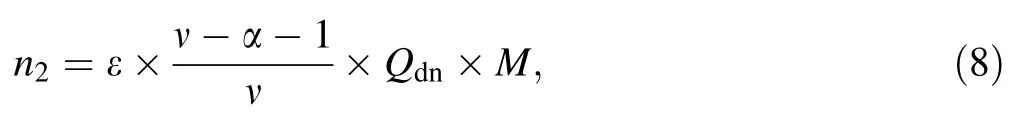
where all the parameters in Eq.(8)are the same as above mentioned.

Substituting Eqs.(6)and(7)into Eq.(8),n2can be expressed as

Combined with Eq.(4)and Eq.(9),Eq.(10)is obtained by

Then,keffcan be obtained as follows

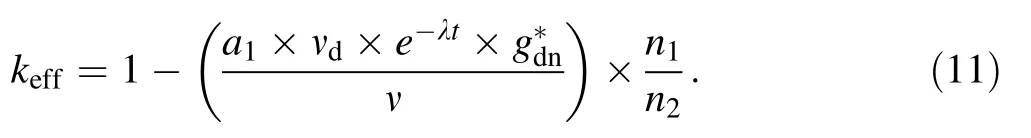
Equation(11)is the basic equation of this work.With the parameters a1,νd,λ,and ν,when n1and n2are measured and g*dnis calculated,the value of keffcan be obtained.

3 Monte Carlo analysis of the effective coef ficient

In order to obtain the factorof 1-th delayed neutrons,the Monte Carlo numerical method was adopted to simulate the reaction and transport process of delayed neutrons and eigen-distribution neutrons,respectively.

As we mentioned above in Eq.(3),the effective coefficient g*is de fined as the ratio of the fixed-source multiplication to the fundamental-mode multiplication.In this work,a neutron source multiplication method was used to acquireof 1-th delayed neutrons.Here,the enriched uranium bare sphere assembly model with 8.805 cm radius and 93.71%enrichment235U is built.A neutron detector was put outside of the system.The detector was spherical and closely surrounded the system,improving the detector ef ficiency.The resultant ef ficiency of leaked neutron detection was 100%.Additionally,the F1 tally card(current integrated over a surface)of MCNP5[20]was adopted to acquire the average importance of every neutron emitted from the neutron source.The calculated formula is:

where J（r，E，t，μ）=|μ|Φ（r，E，t）A is the neutron surface current.

The neutron source distribution produces primary neutrons and simulates the neutron transport process in the subcritical system.The leaked neutrons are statistically integrated the over the detector surface and normalized to delayed neutrons or eigen-neutrons.The normalized value represents the average importance of a source neutron.The average importance of delayed neutrons and eigen-neutrons is acquired,allowing the effective coef ficient,g*,of delayed neutrons to be obtained from their ratio.

In this work,we used 1-th delayed neutrons to analyze the average importance of 1-th delayed neutrons in a Monte Carlo numerical simulation.The distribution of delayed neutron precursors was in accordance with the relative fission rate in the critical nuclear system volume,as what that of the 1-th delayed neutron precursors.Relative delayed neutron emission rates in the volume are required to determine the relative fission rate along the radius.The FMn tally multiplier card in MCNP5 was used to calculate if ssion rate with the form:

where φ(E)is the energy-dependent fluency(particles/cm2)and can be acquired from F5 card;R(E)is an operator of additive and/or multiplicative response functions from the MCNP cross-section libraries or specially designated quantities;and the constant C is any arbitrary scalar quantity that can be used for normalization.Here,R(E),the reaction cross sections are microscopic(with units in barns)corresponding to reaction numbers ‘-6’(total fission cross section)on an FM card.

Nineteen observation points are set at every 0.5-cm interval along the radius.Relative fission rate distribution along the radius is tallied statistically,and the results,which can be used to sample the relative intensity of delayed neutron distribution in the next step,are shown in Fig.1.

One-th delayed neutron distributions are sampled as follows:(1)A DNB card is used to turned off delayed neutron production in MCNP5;(2)enriched uranium bare sphere assembly is first divided into 18 concentric spherical shells along the radius;(3)relative intensity distribution of 1-th delayed neutrons at the initial time in each fissile spherical shell is according to relative fission rate as shown in Fig.1;(4)1-th delayed neutrons,with the average energy of 250 keV,emitted homogeneously in the whole volume;(5)the detector counts of delayed neutrons,ndn,are given via the F1 tally card.

Fig.1 Relative fission rate distribution of enriched uranium bare sphere assembly along the radius from center

As to eigen-neutrons,they are sampled as following:(1)Critical calculation is performed to produce eigen-neutrons via a KCODE card;(2)an SSW card is used and eigenneutron information is written in a WSSA file;(3)an SSR card is used to read the location,direction,and energy distribution of eigen-neutrons from the RSSA file,which called the WSSA file in the former step;(4)the calculation is executed,and detector counts for eigen-neutrons,nen,are recorded with the use of an F1 tally card.

After performing calculations on delayed neutrons and eigen-neutrons,the detector counts for these two neutron types are obtained,and their ratio,ndn/nen,is calculated.This is the effective coef ficient of delayed neutronswhich is 1.22.Statistical uncertainty has been controlled within 1%.

This result is consistent with expectations.From Eq.(3),the 1-th delayed neutrons’effective coef ficientand neutron importance are connected.Neutrons’importance,determined by the neutrons properties,includes direction,energy,and distribution.In other words,when neutrons are injected into subcritical and/or critical system,the neutron population will increase in terms of neutrons′properties.For eigen-distribution neutrons,a kind of fission neutron produced in a critical system;its ‘relative neutron importance’should be 1.For235U nucleus,a low-energy neutron has a greater probability to induce fission.Delayed neutrons have a softer spectrum than prompt neutrons,so they induce fission events more easily than prompt neutrons.Thus,it is reasonable to have an effective coef ficient greater than 1 for delayed neutrons.We can also obtain this conclusion from effective delayed neutron fraction βeff,which is larger than the delayed neutron fraction,β.

Furthermore,comparative studies were conducted to demonstrate that the 1-th delayed neutrons’effective coef ficient,is larger than the effective coef ficient of the total delayed neutrons.In[18]and[21],Yanpeng Yin calculated the effective delayed neutron fraction βeffof CFBR-II,which is 704 pcm.Gregory experimentally studied the effective delayed neutron fraction βeffof fast critical assembly XIX-1,determining it to be 737 pcm.Thus,drawn from experimental results,we could obtain g*of these two according to Eq.(12).Thevalues obtained in this work and comparative results of the two reference works are listed in Table 1.

The average energy of 1-th delayed neutrons(250 keV)is lower than the average energy of total delayed neutrons(about 450 keV),so it is easier for 1-th delayed neutrons to induce fission.It can be concluded that it is reasonable for the effective coef ficient g*of 1-th delayed neutrons to be larger than that of the total delayed neutrons.Owing to this,we propose that using the Monte Carlo method based on the MCNP code to calculate the effective coef ficient of 1-th delayed neutrons is practical.

Spriggs et al.[21]calculated the parameter g*of252Cf spontaneous fission neutrons,and235U and238U spontaneous fission neutrons[16],but did not establish g*of delayed neutrons.As such,our achievement in this work is an effective complement to their theory of equivalent fundamental-mode sources.

4 Experiment apparatus review

Our experimental procedure was performed using the Chinese Fast Burst Reactor-II(CFBR-II).The CFBR-II is a spherical assembly consisting of cast-enriched uranium.Two hemispherical enriched uranium blocks,referred to as upper and lower safety blocks,are driven mechanically.Between the two safety blocks,there is a 31-cm-diameter and 5.2-cm-thick stainless-steel plate.There are three horizontal circular rod slots in the plate,which hold three control rods:an auto-adjustment rod,composition rod,and pulse rod to pass through.Control rods are all made from cast-enriched uranium.The reactivity of the assembly canbe controlled by adjusting the depth to which control rods are inserted.The assembly can work at subcritical,delayed critical,and super prompt critical states.

Table 1 Comparative results ofbetween this work and reference values

Table 1 Comparative results ofbetween this work and reference values

Two BF3proportional counters were used to record the leaked neutrons(proportional to the neutron density in the system)during measurement.A BF3proportional counter,SZJ-1 type,the production of Beijing Nuclear Instrument Factory,was put in the paraf fin barrel to construct the Hanson long counter,along with a preampli fier,a highvoltage–power supply,a main ampli fier,and a multi-scalar to constitute the measurement system.The front of the detectors was 180 cm away from the center of the system,and the dead time of the detectors was 3 μs.Figure 2 demonstrates the system structure and the location of detectors.

5 Experiments and results analysis

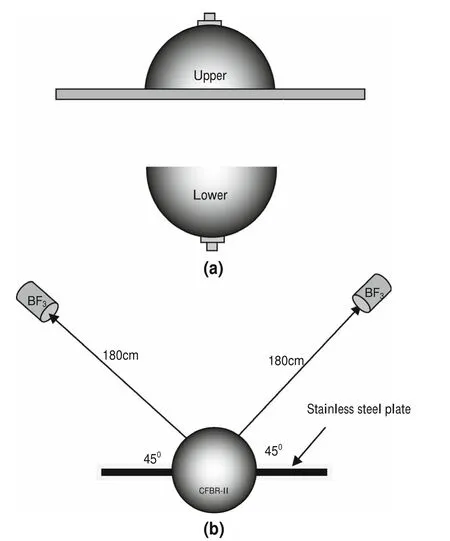
Fig.2 a Schematic of CFBR-II;b location of detectors

We performed experiments as follows:(1)The reactor was kept in critical state for more than 10 min and the delayed neutron precursors reached saturation,at which point the neutron detectors count rate(n1)in experiments was 2.07e7 s-1(case 1:50 W running power)and 1.25e7 s-1(case 2:30 W running power);(2)we drew out a control rod(made of enriched uranium)and separated the two safety blocks promptly,indicating the system would be in a shutdown state and the fission events stopped,precursors could not produce,and the ones that already existed in the system decayed subsequently;300 s after the reactor shut down,only 1-th delayed neutrons existed in the system and other groups of delayed neutrons disappeared,as we outlined in Sect.3;(3)upper and lower safety blocks of the assembly connected together rapidly,taking reactor from a shutdown state to a subcritical state.To this point,the multiplication of 1-th delayed neutrons had been realized.Two neutron detectors counted the leaked neutrons of the experimental system.Taking into consideration the fluctuation and noise effect on the count rate,the delayed neutrons’behaviors after the system shut down are shown in Fig.3.Curves were fitted with an exponential function,and the half-life of87Br was obtained as 55.45 and 54.79 s,respectively,in these two experiments.The results are in good agreement with the half-life of87Br,(ENDF/B-VI).

The supplementary speci fications for the neutron count rate n1and n2are as follows.These rates are acquired from a common,current method,which is often used when the neutron count rate is too large for detectors to handle.A brief description of the method is as follows.First,the relationship between electric current and neutron count rate is determined from the ionization chamber and the neutron detector,working simultaneously at low power.The detector count rate when the nuclear assembly is working at high power can be determined by extrapolation from readings obtained via the ionization chamber.

With the constants a1(0.0395 for 235U),νd(0.0163 for 235U),λ(0.0127 s-1for 87Br),ν(2.59 for235U prompt fission)[22],detector count rates n1and n2,and the calculated(1.22),the average value of kefffrom all points in Fig.3a,b can be obtained based on Eq.(11).The average value of keffwas 0.9921 and 0.9969,respectively,in these two experiments.The comparison between the results obtained through the reference method(positive period method:identi fied byand our proposed method(identi fied by keff)is calculated by this formula:The comparison results are listed in Table 2.The accuracy of the results can be attributed to the power of the nucleus device when kept in steady mode.The reactor ran at a power level of 50 W in case 1 and 30 W in case 2.The greater the power level,the more fission neutrons are produced in the system,the more neutrons leak from reactor,and more easily the neutron detectors catch the neutrons.This means that the count rate of detectors is in fluenced by the power of the nuclear system.Thus,the statistical uncertainty of detectors is lower in case 1 and its results are closer to the positive period method results.

Here is the complementary to the reference method(the positive period method).The control rods of CFBR-II were calibrated using the positive period method.The curves describing the relationship between reactivity and the position of control rods are well established.When the reactivity of the system is changed by adjusting the position of the control rods,the reactivity of the system can be read off the curves.

Fig.3 Count rate of delayed neutrons leaked from assembly after two safety blocks separated.Before separation,the assembly has ran at a power level of 50 W in case 1(a)and 30 W in case 2(b)

Table 2 Comparative results of keffbetween this work and positive period method

6 Conclusion

A methodology to use delayed neutrons as the neutron source in neutron multiplication experiments to acquire keffwas first proposed and investigated via preliminary NSM experiments on CFBR-II.The evaluated results were approximately equal to the reference method(the positive period method).

An experimental delayed neutron multiplication method was established,and the Monte Carlo method was adopted to analyze the effective coef ficient g*of delayed neutrons.The effective neutron multiplication factorkeffwas obtained experimentally in two subcritical states.The results were approximately equal to the reference method(the positive period method)and were not heavily dependent on detection ef ficiency.We posit that running the reactor at an appropriate power level would reduce the relative differences in experimental results.We conclude that measurement of keffby delayed neutron multiplication in subcritical systems,as we outlined in this paper,is feasible for simple subcritical apparatus,such as CFBR-II.

1.Y.Q.Shi,Q.F.Zhu,P.Xia et al.,Neutron source multiplication method research in reactor physics experimen.Nucl.Sci.Eng.25,14–19(2005).https://doi.org/10.3321/j.issn:0258-0918.2005.01.002(in Chinese)

2.G.Truchet,W.F.G.van Rooijen,Y.Shimazu et al.,Application of the modi fied neutron source multiplication method to the prototype FBR Monju.Ann.Nucl.Energy 51,94–106(2013).https://doi.org/10.1016/j.anucene.2012.07.040

3.G.M.Sun,M.S.Cheng,Z.M.Dai,Preliminary analysis of fuel management for a small modular molten salt fast reactor.Nucl.Tech.39,070603(2016).https://doi.org/10.11889/j.0253-3219.2016.hjs.39.070603.(in Chinese)

4.K.Yang,J.G.Chen,X.Z.Cai,Using the neutron balance method to access the feed fuel requirements for CANDLE.Nucl.Tech.39,060601(2016).https://doi.org/10.11889/j.0253-3219.2016.hjs.39.060601.(in Chinese)

5.T.Endo,A.Yamamoto,Y.Yamane,Detected-neutron multiplication factor measured by neutron source multiplication method.Ann.Nucl.Energy 38,2417–2427(2011).https://doi.org/10.1016/j.anucene.2011.01.007

6.B.Ye,L.N.Zeng,Y.P.Yin et al.,Measurement of keffwith an improved neutron sourcemultiplication method based on numerical analysis.Nucl.Sci.Tech.25,020602(2014).https://doi.org/10.13538/j.1001-8042/nst.25.020602

7.H.W.Xiao,G.M.Liu,H.Yao et al.,In fluence of extended low power operation on neutronics parameters of CNP600.Nucl.Tech.39,110602(2016).https://doi.org/10.11889/j.0253-3219.2016.hjs.39.110602.(in Chinese)

8.H.Shahbunder,C.H.Pyeon,T.Misawa et al.,Experimental analysis for neutron multiplication by using reaction rate distribution in accelerator-driven system.Ann.Nucl.Energy 37,592–597(2010).https://doi.org/10.1016/j.anucene.2009.12.022

9.H.Shahbunder,C.H.Pyeon,T.Misawa et al.,Subcritical multiplication factor and source ef ficiency in accelerator-driven system.Ann.Nucl.Energy 37,1214–1222(2010).https://doi.org/10.1016/j.anucene.2010.04.010

10.H.Shahbunder,C.H.Pyeon,T.Misawa et al.,Effects of neutron spectrum and external neutron source on neutron multiplication parameters in accelerator-driven system.Ann.Nucl.Energy 37,1785–1791 (2010).https://doi.org/10.1016/j.anucene.2010.07.003

11.C.M.Persson,P.Seltborg,A.Ahlander et al.,Analysis of reactivity determination methods in the subcritical experiment Yalina.Nucl.Instrum.Method A 554,374–383(2005).https://doi.org/10.1016/j.nima.2005.07.058

12.C.M.Persson,A.Fokau,I.Sera fimovich et al.,Pulsed neutron source measurementsin the subcriticalADS experiment YALINA-Booster.Ann.Nucl.Energy 35,2357–2364(2008).https://doi.org/10.1016/j.anucene.2008.07.011

13.D.L.Chichester,M.T.Kinlaw,The MARVEL assembly for neutron multiplication.Appl.Radiat.Isot.80,42–48(2013).https://doi.org/10.1016/j.apradiso.2013.05.012

14.R.Soule,W.Assal,P.Chaussonnet et al.,Neutronic studies in support of accelerator-driven systems:the MUSE experiments in the MASURCA facility.Nucl.Sci.Eng.148,124–152(2004).https://doi.org/10.13182/NSE01-13C

15.A.Billebaud,R.Brissot,C.LeBrun et al.,Prompt multiplication factor measurements in subcritical systems:From MUSE experiment to a demonstration ADS.Prog.Nucl.Energy 49,142–160(2007).https://doi.org/10.1016/j.pnucene.2006.11.001

16.G.D.Spriggs,R.D.Busch,T.Sakurai et al.,The equivalent fundamental-mode source.Ann.Nucl.Energy 26,237–264(1999).https://doi.org/10.1016/S0306-4549(98)00048-614

17.J.F.Du,X.Q.Fan,Calculation of effective coef ficient of spontaneity fission neutron source in CFBR-II reactor.Nucl.Power Eng.31,131–133(2010).https://doi.org/10.7538/yzk.2013.47.04.0619

18.Y.P.Yin,C.Zheng,P.Huang,Calculation of CFBR-II’s multiplication-reactivity conversion factor.Chin.J.Comput.Phys.27,799–804(2010).https://doi.org/10.3969/j.issn.1001-246X.2010.06.002

19.C.Zheng,Q.Wang,M.Li et al.,Measurement of total fission number by delayed neutron method for burst reactor.Atom.Energy.Sci.Technol.41,699–701(2007).https://doi.org/10.3969/j.issn.1000-6931.2007.06.014.(in Chinese)

20.X-5 Monte Carlo Team Los Alamos National Laboratory,MCNP-A General Monte Carlo N-Particle Transport Code,Version 5.LA-UR-03-1987(2008)

21.G.D.Spriggs,T.Sakurai,S.Okajima,Rossi-α and βeffmeasurements in a fast critical assembly.Prog.Nucl.Energy 35,169–181(1999).https://doi.org/10.1016/S0149-1970(99)00010-4

22.D.E.Gremyachkin,V.M.Piksaikin,K.V.Mitrofanov et al.,Veri fication of the evaluated fission product yields data from the neutron induced fission of235U,238U and239Pu based on the delayed neutron characteristics.Prog.Nucl.Energy 83,13–25(2015).https://doi.org/10.1016/j.pnucene.2015.02.016