基于改进的单亲遗传算法的枝状集输管网优化

王菲菲 赵金成

1.中国石油大学胜利学院, 山东 东营 257061;2.中海油能源发展股份有限公司工程技术分公司, 天津 300452

0 前言

枝状管网投资较省[1-2],因此在集输管网尤其是油井呈狭长状分布时经常被采用。遗传算法通过对由大量个体组成的种群进行反复迭代来实现优化[3],需要极大的计算量。而集输管网规模庞大,枝状管网拓扑结构复杂[4],造成求解数据量大,求解效率低,以往多采用分级优化算法,如Prim、Dijkstra及Kruskal等算法进行大规模枝状集输管网的优化[5-7]。而分级优化只能以管长最短为目标,无法实现管网系统的费用最省[8-9]。尽管有许多专家学者对遗传算法在管网优化中的应用进行了研究,但大多数局限于拓扑结构简单的星状管网[10-11]、小规模枝状管网[12-14]、井组划分及站场位置优化[15-16]，以及管网的运行参数优化[17-20],真正解决大规模枝状集输管网全局优化问题的还较少。

为了实现对大规模枝状集输管网的全局优化,提高遗传算法的运行效率,本文提出了一种管网初步连接图的生成方法,对传统单亲遗传算法(SPGA)的编码方式、选择算子及遗传操作手段进行了改进,并基于改进的单亲遗传算法对国内某油田的枝状集输管网进行了优化研究。

1 优化数学模型

以费用最省为目标建立管网优化的数学模型，如下：

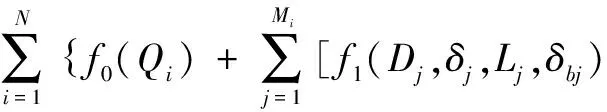
+f2(prj,pzj,Qj)+f3(Dj,Trj,Tzj,Lj)]}

(1)

式(1)中：N为站场数目,个；Mi为每个站场下的管线数目，条；f0为站场i的建站费用，与站场处理量有关，万元；f1为管材费，与管径、管长、壁厚及保温层厚度有关[21]，万元；f2为动力费，与流量、管线起点压力及终点压力有关，万元；f3为热力费，与管径、起点温度、终点温度及管长有关，万元；Qi为站场处理量，m3/d；Dj为管径，mm；Lj为管长，m；δj为管线壁厚，mm；δbj为保温层厚度，mm；Qj为管道流量，m3/d；prj为管线起点压力，MPa；pzj为管线终点压力，MPa；Trj为管线起点温度，℃；Tzj为管线终点温度，℃。

约束条件为：

1)管线起终点压力应在最低入站压力与最高出站压力之间：

pmin≤pri≤pmax；pmin≤pzi≤pmax(i=1,2,3,…M)

2)管线起点及终点温度应在最低入站温度与最高出站温度之间：

Tmin≤Tri≤Tmax；Tmin≤Tzi≤Tmax(i=1,2,3,…M)

3)管线壁厚应进行压力校核，并满足管径系列中的壁厚条件：

δi≥δ(Di,pi) (i=1,2,3,…M)

4)管线的流速应在最大及最小经济流速之间：

vmin≤vi≤vmax(i=1,2,3,…M)

2 管网初步连接图

集输管网与城市燃气管网及给排水管网不同,在其布置过程中不需要沿道路铺设,油井可任意两两连接,并不存在天然的管网初步连接,这使得其中存在大量绕行管线,形成大量不合理解,大大降低单亲遗传算法的求解速率。本文提出通过生成管网初步连接图的方法来避免管线绕行,提高求解速率及效率。管网初步连接图生成原理见图1，两两遍历所有油井(如i、j),在两油井周围建立矩形域(如ABCD),若矩形域中包含其它油井(如k),则两井不连接，见图1 a),否则连接，见图1 b)。其中矩形域的生成方式为:

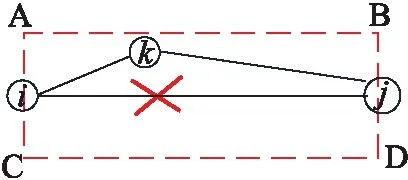
a)

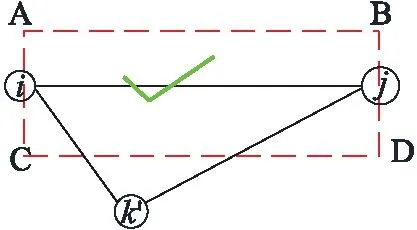
b)

1)过两井并垂直于连接线作直线确定边AC和BD;

2)通过定义管网初步连接图生成比确定边AB和CD。逐步遍历所有油井后形成管网初步连接图,在管网初步连接图的基础上再进行遗传算法优化求解。

3 改进的单亲遗传算法求解

3.1 编码方式及其改进

3.2 遗传算子及其改进

本文用到的遗传算子包括换位算子、倒位算子、移位算子及选择算子。

3.2.1 换位算子

通过交换两基因串的位置来得到新的个体,如:1101011001→1001011101。

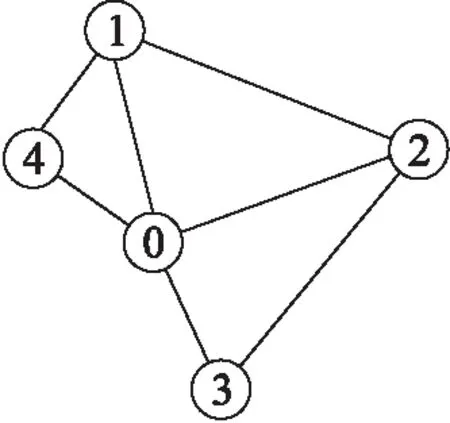
a) 管网初步连接图

b) 实际连接方案

3.2.2 倒位算子

通过颠倒某基因串的顺序来得到新的个体,如:1101011001→1100110101。

3.2.3 移位算子

通过将某基因串整体移动来产生新的个体,如:1101011001→1110001011。

换位、倒位及移位算子可进行单点操作及多点操作[23]。单点操作即仅对一对基因串进行操作,操作精细，不易错过最优解，但进化速度较慢；多点操作则对多对基因串进行操作，进化速度较快，但容易错过最优解。为克服单点操作及多点操作的缺点，提高算法的收敛速度及优化效果,本文采用代间交叉的遗传操作手段,偶数与奇数代交替进行单点与多点遗传操作。

3.2.4 选择算子及其改进

本文通过比例选择得到下一代种群。但若采用传统的比例选择算子,在进化前期算法易陷入局部收敛,在进化后期算法的优化效果不好。因此对传统的比例选择算子进行了改进:将新一代种群中的个体按照适应度大小进行编号,并让每个个体的适应度等于其编号,而后再进行后续遗传操作。这样能够较好地解决单亲遗传算法前期易陷入局部收敛及后期优化效果差的问题。

3.3 染色体评估

染色体评估是为了求解每个染色体的适应度并求出其中的最优解,其步骤为:1)染色体解码为管网连接;2)求解总费用,并代入适应度函数F=1/(1+总费用),得到适应度;3)适应度最大的为最优解。

3.4 求解步骤

本文采用先繁殖后选择下一代种群的运行方式,这样有利于保留上一代的优势,其步骤见图3。其中,产生初始种群及基因重组的过程中,每得到一个新个体都要进行连通性检验,若不连通则要重新生成。

4 优化结果分析

为对比分析算法改进的效果,本文选用国内某油田的油井数据进行了实例计算及结果分析。

4.1 管网初步连接图的效果

本文结合实例计算对管网初步连接图的效果进行了对比研究,见图4。其中,生成比为0表示不采用管网初步连接图。可以看出,采用管网初步连接图后总费用明显降低。可见,采用管网初步连接图明显改善了优化效果。另外,在不采用管网初步连接图时,计算时间明显偏高。因此,采用管网初步连接图也显著提高了优化效率。

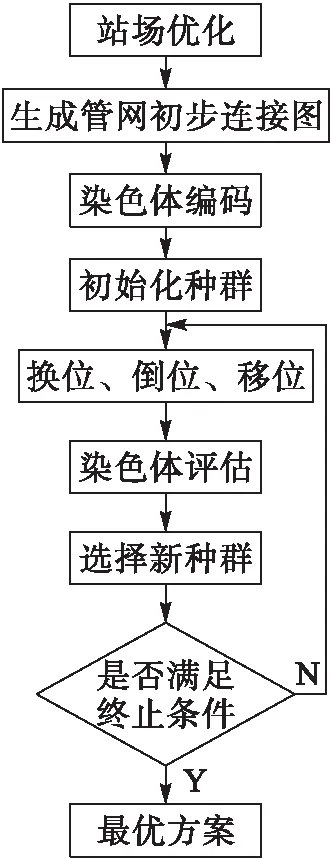
图3 优化求解步骤

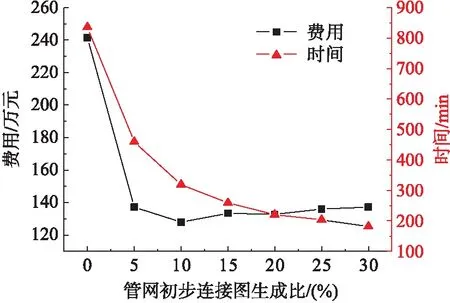
图4 管网初步连接图对优化效率及效果的影响

4.2 遗传操作手段的改进效果

由图5可以看出,相比于单一的单点遗传操作,采用代间交叉操作后,算法的收敛速度明显加快,最终的优化效果也更好。

4.3 选择算子的改进效果

由图6可以看出,对传统的比例选择算子进行改进后,进化前期及后期的优化效果得到了明显改善,较好地解决了前期易陷入局部收敛及后期优化效果差的问题。

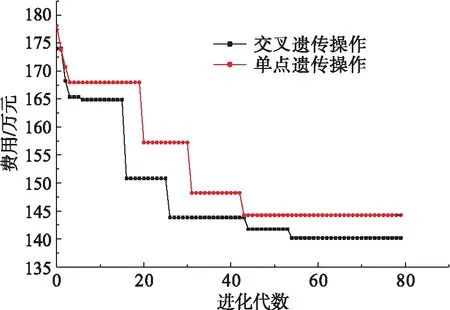
图5 遗传操作手段对优化效果的影响

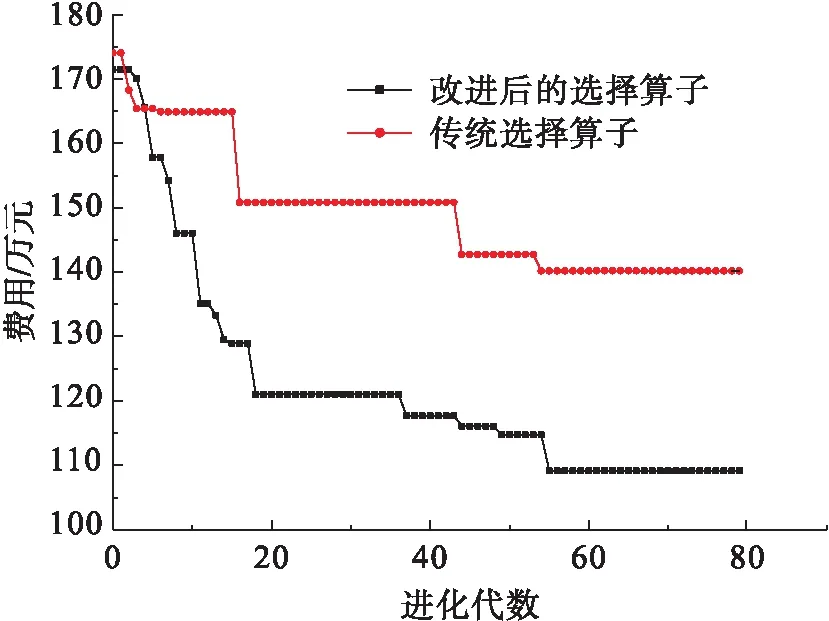
图6 选择算子的改进对优化效果的影响

4.4 集输管网优化实例

本文采用改进的单亲遗传算法对国内某油田的集输管网进行了优化设计。该油田共有油井150口,采用“油井-增压站-联合站”两级布站,拟建1个联合站,5个增压站。本例中采用油井到增压站、再从增压站到联合站的两级输送方式,其布局见图7。

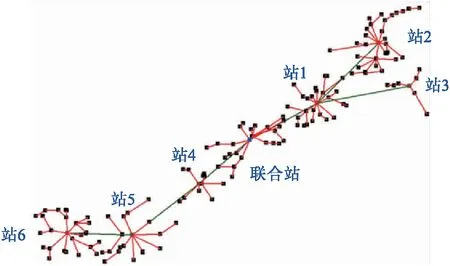
图7 集输管网优化实例

另外,本文对不同算法最优方案的费用进行了对比分析,见表1。其中,管材费包括管道费及保温费;建站费为各站场的总建设费;动力费为运行过程中油品的加压费用;热力费为运行过程中的加热费用;所有费用都为寿命期总费用,并折合到寿命期末。通过对比可以看出,集输系统的总费用主要取决于建站费及动力费,管材费及热力费占比较少。而Prim算法、Kruskal算法以管长最短为目标,Dijkstra算法以路径最短为目标,这三种算法管长较短,管材费较少,但其他费用较高。改进后的单亲遗传算法则以总费用最省为目标,增大总管长,管材费相应较高,但使得动力费及建站费显著降低,因此总费用最低。可见,改进的单亲遗传算法的优化效果明显优于分级优化算法,真正达到了费用最省的目的。

表1不同算法的优化效果对比万元

5 结论

本文建立了全局优化模型,对单亲遗传算法进行了改进:

1)通过生成管网初步连接图及代间交叉遗传操作提高了优化效率。

2)通过改进选择算子显著改善了算法效果。

3)改进的单亲遗传算法解决了大规模枝状集输管网的全局优化问题。

[1] 梁永图,张浩然,马 晶,等.油气田集输管网系统优化研究进展[J].油气储运,2016,35(7):685-690.

Liang Yongtu, Zhang Haoran, Ma Jing, et al. Advances in Optimization Study of Oil and Gas Field Gathering Pipeline Network [J]. Oil & Gas Storage and Transportation, 2016, 35 (7): 685-690.

[2] 任玉鸿,梁永图,何国玺.页岩气地面集输管网拓扑优化[J].油气田地面工程,2016,35(6):54-57.

Ren Yuhong, Liang Yongtu, He Guoxi. The Topology Optimization of Shale Gas Gathering Pipeline Network [J]. Oil & Gas Storage and Transportation, 2016, 35 (6): 54-57.

[3] 周 明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999:6.

Zhou Ming, Sun Shudong. Genetic Algorithms:Theory and Applications [M]. Beijing: National Defend Industry Press, 1999: 6.

[4] 殷桂琴,张公社,刘志军,等.树枝状注水管网布局优化设计方法研究[J].断块油气田,2006,13(5):58-60.

Yin Guiqin, Zhang Gongshe, Liu Zhijun, et al. Method for Layout Optimization Design of Dendritic Waterflooding Pipeline Networks [J]. Fault-Block Oil and Gas Field, 2006, 13 (5): 58-60.

[5] 徐国栋,梁 政.气田集输管网布局优化研究[J].石油规划设计,2004,15(6):18-21.

Xu Guodong, Liang Zheng. Optimization of Gathering Pipeline Network in Gas Field [J]. Petroleum Planning and Engineering, 2004, 15 (6): 18-21.

[6] 王洪元,卜 莹,潘 操.基于遗传蚁群算法的气田集输管网优化方法[J].计算机与应用化学,2012,29(12):1495-1498.

Wang Hongyuan, Bu Ying, Pan Cao. An Optimization Method Based on GA—ACA for Gas Gathering Pipeline Network in a Gas Field [J]. Computers and Applied Chemistry, 2012, 29 (12): 1495-1498.

[7] 蒋 洪,张 黎,任广欣,等.煤层气地面集输管网优化[J].天然气与石油,2013,31(1):8-12.

Jiang Hong, Zhang Li, Ren Guangxin, et al. Optimization of Coalbed Methane (CBM) Surface Gathering and Transportation Pipeline Network [J]. Natural Gas and Oil, 2013, 31 (1): 8-12.

[8] 刘文艳,叶 枫.单亲遗传算法在天然气管网布局优化中的应用[J].科学技术与工程,2011,11(6):1351-1354.

Liu Wenyan, Ye Feng. Single Parent Genetic Algorithm Applied in Layout Optimization of Gas Network [J]. Science Technology and Engineering, 2011, 11 (6): 1351—1354.

[9] 尚文芳.基于网络分级优化和Dijkstra算法的最短路径求解改进[J].廊坊师范学院学报:自然科学版,2014,14(2):5-7.

Shang Wenfang. Improved Dijkstra Shortest Path Algorithm Based on Net Optimization [J]. Journal of Langfang Teachers University: Natural Science Edition, 2014, 14 (2): 5-7.

[10] 杨建军,战 红,刘 扬,等.星状原油集输管网拓扑优化的混合遗传算法[J].西南石油大学学报:自然科学版,2008,30(4):166-169.

Yang Jianjun, Zhan Hong, Liu Yang, et al. Hybrid Genetic Algorithm for Topology Optimization of Stellated Oil Gathering and Transportation Pipeline Network [J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2008, 30 (4): 166-169.

[11] 刘 刚,许继凯,国志刚,等.星状集输管网拓扑结构的整体优化[J].中国石油大学学报:自然科学版,2016,40(4):133-140.

Liu Gang, Xu Jikai, Guo Zhigang, et al. Global Optimization of Topological Structure for Radial Pattern Gathering Pipe Network [J]. Journal of China University of Petroleum: Edition of Natural Science, 2016, 40 (4): 133-140.

[12] 邱金亮,王 静,左传英,等.基于组合遗传算法的树状管网整体优化设计模型[J].中国农村水利水电,2013,(9):26-28.

Qiu Jinliang, Wang Jing, Zuo Chuanying, et al. Tree Pipe Network Optimization Design Method Based on Combined Genetic Algorithm [J]. China Rural Water and Hydropower, 2013, (9): 26-28.

[13] 周荣敏,雷延峰.基于改进单亲遗传算法的树状管网布置优化[J].水利学报,2012,43(10):1243-1247.

Zhou Rongmin, Lei Yanfeng. Optimal Layout of Tree Pipe Networks Based on Improved Single Parent Genetic Algorithm [J]. Journal of Hydraulic Engineering, 2012, 43 (10): 1243-1247.

[14] 郜 瑜.单亲遗传算法进行树状管网优化[J].山西科技,2007,(3):51-52.

Gao Yu. Optimization of Tree Pipe Network with Single Parent Genetic Algorithm [J]. Shanxi Science and Technology, 2007, (3): 51-52.

[15] 曹 迪,马国光,左 敏.基于遗传算法的集输管网整体布局优化[J].辽宁化工,2016,45(9):1218-1220.

Cao Di, Ma Guoguang, Zuo Min. Optimization of Gathering Pipeline Network Overall Layout Based on Genetic Algorithm [J]. Liaoning Chemical Industry, 2016, 45 (9): 1218-1220.

[16] 吴华丽,陈坤明,王效东,等.基于遗传算法的集输管网井组划分[J].管道技术与设备,2007,(6):1-2.

Wu Huali, Chen Kunming, Wang Xiaodong, et al. Well Division of Gathering and Transferring Pipeline Networks by Genetic Algorithm [J]. Pipeline Technique and Equipment, 2007, (6): 1-2.

[17] 高松竹,汪玉春,许 萍.用改进遗传算法解压气站优化运行问题[J].天然气与石油,2003,21(3):17-19.

Gao Songzhu, Wang Yuchun, Xu Ping. Using Improved Genetic Algorithm to Solve the Optimal Operation Problem of Compressor Station [J]. Natural Gas and Oil, 2003, 21 (3): 17-19.

[18] 马孝义,范兴业,赵文举,等.基于整数编码遗传算法的树状灌溉管网优化设计方法[J].水利学报,2008,39(3):373-379.

Ma Xiaoyi, Fan Xingye, Zhao Wenju, et al. Tree-type Pipe Network Optimization Design Method Based on Integer Coding Genetic Algorithm [J]. Journal of Hydraulic Engineering, 2008, 39 (3): 373-379.

[19] 崔之健,王 菁,张晓阳,等.基于遗传算法的油气集输管网运行效率优化[J].西安石油大学学报:自然科学版,2008,23(6):59-62.

Cui Zhijian, Wang Jing, Zhang Xiaoyang, et al. Optimization of the Operation Efficiency of Oil-Gas Gathering Pipeline Network Based on Genetic Algorithm [J]. Journal of Xi’an Shiyou University: Natural Science Edition, 2008, 23 (6): 59-62.

[20] 李卫华,李长俊.基于遗传算法的天然气集输管网参数优化设计[J].天然气工业,2005,25(2):158-160.

Li Weihua, Li Changjun. Parameter-optimized Design of Gas Gathering and Transmission System by Heredity Solution [J]. Natural Gas Industry, 2005, 25 (2): 158-160.

[21] 李自力,孙云峰,张子波,等.普光高含硫气田集输管网优化[J].石油学报,2011,32(5):872-876.

Li Zili, Sun Yunfeng, Zhang Zibo, et al. Optimization Design of a Gathering Pipe Network of Natural Gas with High H2S from the Puguang Gas Field [J]. Acta Petrolei Sinica, 2011, 32 (5): 872-876.

[22] 陈永建,周 艳.遗传算法编码方式的应用及其改进算法的研究[J].太原师范学院学报:自然科学版,2008,7(2):76-78.

Chen Yongjian, Zhou Yan. Application of Coding Genetic Algorithm and Its Improvement Research [J]. Journal of Taiyuan Normal University: Natural Science Edition, 2008, 7 (2): 76-78.

[23] 李茂军.单亲遗传算法理论及应用[D].长沙:湖南大学,2002.

Li Maojun. The Theory and Application of Partheno-genetie Algorithm [D]. Changsha: Hunan University, 2002.