巧用列表法解决循环结构问题
李鹏
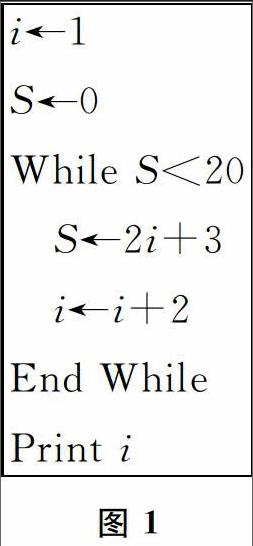
算法中主要涉及三种基本逻辑结构:顺序结构、选择结构和循环结构,其中循环结构是这三者中最重要的一种结构.很多同学对循环结构中变量的变化情况的掌握存在比较大的困难,具体表现在随着循环次数的增加,对某些变量的变化情况逐渐变得模糊、混淆,进而对循环的起点条件、循环次数、循环终止条件、最终结果、循环功能等无法准确把握.
如何才能突破循环结构问题的难点呢?建议同学们利用列举法,通过列举去追踪循环结构中的变量,明确各个变量在进入循环体后的值,观察和归纳出变量在退出循环时应输出的值,进而得到问题的答案.本文将针对不同的题型,通过列表法追踪变量的变化,来揭示列表法对解决循环结构问题的作用.
一、求输出结果
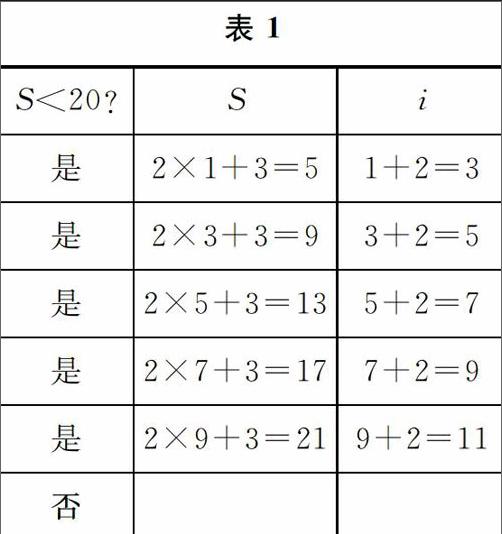
例1 执行如图1所示的伪代码,输出的值为
解 伪代码的程序语句执行中的数据变化如表1所示,当S<20时可执行循环体,当S≥20时退出循环,此时输出i=11.
点评 本题主要考查“当型”循环语句,通过对程序语言的读取,再根据所给循环结构,判断出S≥20时的输出结果.由程序运行过程看,这是一个累加的问题.解题时,可通过对条件S<20的判断,逐步演算S的结果,通过判断,可知该程序演算过程需运行5次,i的值变为11,此时程序不再进入循环体,继而输出.
总结 ①无论是“直到型”还是“当型”循环结构,列表时均以判断框或判断语句作为计算每一组变量值的起始;
②列表时,表中的变量白左至有的顺序应与循环体中各变量发生变化的先后顺序保持一致,便于明确每个变量的当前值是哪次循环得到的.例2 执行图2的程序框图,如果输入的x=0,y=l,n=l,则输出x,y的值满足(
)A.y=2x
B.V=3xC.V=4x
D.V=5x
解 由表2可得,当x=3/2,y=6时,程序框图退出循环,故满足y=4x的关系式,选C.
点评 本题的循环结构中,循环体看起来好像被判断框分成了两部分:x,y在判断框前开始第一次变化,而n在判断框后才开始第一次变化.当抓住了“判断框作为计算每一组变量值的起始”这个关键点,第一组变量的值就不难确定为n=2,x=1/2,y=2”,而不是“x=0,y=1,n=2”;同时也不难确定,列表中变量的先后顺序是”在前,而x,y在后.
二、求循环初值
例3 某算法流程图如图3所示,该程序运行后,若输出的x=15,则实数a等于
解 如表3所示,第一次循环x=2a+1,n=2,第二次循环x=4a+3,n=3,第三次循环x=8a+7,n=4>3,结束循环输出x=8a+7=15,a=1.
点评 本题根据判断框内的条件,通过列表法列举出循环结束时所输出的x,再令其结果8a+7=15,解出所求的a的值.特别注意,如果列举时次数过多,可以采用部分列举,再寻求规律,进而归纳出结果.
例4程序的框图如图4,如果上述程序运行的结果为S=132,那么判断框中横线上应填入的数字是
解 由流程图可知,此程序目的是求几个数的连乘积,第一次乘入的数是12,以后所乘的数依次减少1,由于132=11×12,如表所示,可知一共循环两次,当k=11时,要满足循环条件,而当k=10时退出循环,故判断框中可填k≤10.
點评 本题要求写出循环条件,只要用列表法得到与输出的S值对应的k值,判断框内的条件便可确定.
四、求循环次数
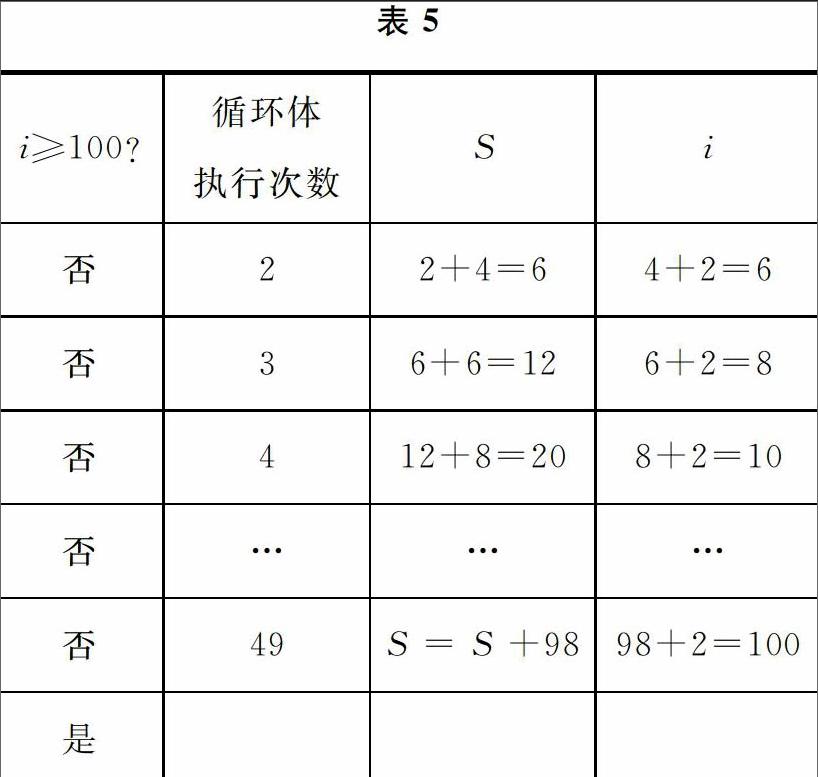
例5 如图5所示的程序框图中循环体执行的次数是______.
解 如流程图所示,首先执行循环体,再进行条件判断.根据列表不难发现,最后一次执行循环体是当“i=98+2 =100”时,然后退出循环并输出S,所以循环体执行次数为49次.
点评 本题是根据循环结构求循环体执行次数的问题,一般来说此类题型中流程图循环体执行次数比较多,可以通过列表法分析得到计数变量i和求和变量S的变化规律,再判断循环体执行的次数.
含循环结构的流程图、伪代码问题是算法学习中的重点和难点,将其表格化进行列举,寻找规律,是一个简单、有效的方法.对循环结构本质的理解始终是解决这类问题的基础,列表法用来追踪循环语句中的变量,记录其变化情况.列表不仅条理清晰、易于观察,而且可以帮助同学们更容易理解循环结构,化繁为简.endprint

