基于链路动态变化的产业网络预测模型研究
王 斌王文平费为银
(1.安徽工程大学数理学院,安徽芜湖241000;2.东南大学经济管理学院,江苏南京211189)
1 引 言
经济投入产出系统能够被构建成产业网络,节点表示系统中的各个产业或企业,链路表示相互之间的物质、副产品和能量的循环流动.网络分析方法能够探讨产业网络的结构和性质[1],能够测量网络中各个节点之间的交流,而且能够解释相互之间的影响和信息流动[2-4],因而它是分析经济投入产出系统的一个有力工具.目前,产业网络的构建主要基于投入产出表所反映的信息,并据此研究产业网络结构特征及其演化,为产业结构的优化、以及产业的转型升级提供合理的政策建议.如文献[5—10]从整体的角度,以某个年份的投入产出表为基础,研究产业网络的无标度性、幂律分布和最大关联树等基本特征.文献[11—15]从个体的角度,以几个年份的投入产出表为基础,研究产业网络内的主导产业,如何在国家产业结构调整和优化升级过程中发挥各自的优势和作用,以及探讨产业网络的演化,分析集群网络之间的互动及部门角色的变动问题.可见,投入产出表对于研究产业网络是多么的重要.但从时间维度看,基于投入产出表之上的产业网络,只是研究了某些年份的产业网络结构特征,而没能克服借助静态、历史的数据研究产业网络的局限.再从现实情况看,囿于编制投入产出表需要消耗大量的人力和物力,中国的投入产出表只是每五年编制一次,且表的公布年份距编表年份至少也会有2年~3年.较长的编表周期导致投入产出表注定是一种历史数据,那么分析以该表为基础的产业网络,对于经济结构变化较大的转型经济体来说,数年的滞后可能会影响研究结果的正确性.因此,及时、准确地预测产业网络具有重要的意义.
若能克服投入产出表跨度大,不能及时、准确反映产业网络结构变化的缺点,使得产业网络的预测变得便捷可行,则能依据若干个年份的投入产出表,对产业网络进行及时、动态的分析.事实上,随着时间的演化,产业网络中原有的链路可能消失或产生新的链路,从而表现出了较强的动态性和复杂性,处理如此问题选择社会网络分析法(SNA)十分适宜[16],链路预测又是网络分析法中的重要任务之一.链路预测是指,依据已知的网络结构等信息,预测网络中尚未链接的两个节点之间将来产生链接可能性的大小,该理论已经被广泛应用于各种网络分析当中[17-19].因此,链路预测是尽可能的推断出两个节点之间链接存在的可能性,具有重要的理论和实际意义.
在真实的网络中,相比于用实验结果去推断两个节点之间是否有相互作用关系,利用链路预测去预估节点将来的行为,或者识别两个节点之间未来的链接,成本更为低廉.例如,在新陈代谢网络与蛋白质相互作用网络中,需要通过大量实验结果推断节点之间是否存在相互作用关系[20],高额的实验成本自然不可避免.降低实验成本,并且不失准确地推断结论的理想方法,是针对这些网络的结构特性、设计出一套足够精确的链路预测算法,然后实验在预测结果的指导下进行.已经有许多学者研究了链路预测的问题,这些研究主要是基于当前网络的结构性质,预测任意两个节点之间将来发生链接的概率,且研究的科学领域众多.例如,Goldberg等[21]利用蛋白质网络的局部集聚性,预测了缺失的链接;Manning等[22]构建了一个信息检索网络,节点代表关键词或分类文件,通过预测两者之间的关系,区分了未经辨识的文件.图书推荐网络是链路预测的另一个事例,Chen等[23]在用户和书目之间建立了许多图论测度,以期向用户做图书推荐.此系统是一个用户—图书的二部网络,链路表示用户对某种图书的偏好.链路预测也可以被用于分析演化网络,例如,Zhou等[24]利用链路预测理论分析了互联网将来的形状;Juszczyszyn等[25]利用马尔科夫链构建了一个链路预测模型,分析了大学邮箱网络的子图结构随时间的演化情况.解决链路预测问题一个最简单的方法是所谓的得分算法,其中基于相似性的得分预测算法能够得到很好的预测结果,并且网络的拓扑结构性质能够帮助选择合适的相似性指标[26,27].随后,学者们又考虑了加权网络上的链路预测问题,发现含权指标的得分预测效果要好于无权的预测方法[28].这些研究都充分体现了得分预测算法的简洁性,并且得分预测方法很容易和其他的方法相结合.例如,Aaron等[29]应用层级结构知识预测了丢失的链接,其中层级结构可以解释许多网络所表现出的右偏态度分布、高集聚系数和最短路径长度性质.Chungmok等[30]从网络度分布的角度,用数学规划方法预测了网络将来的结构,其中,预测问题被转化为整数规划问题,这样做的目的是以便最大化链路预测得分总和.Chen等[31]构建了一个快速的相似性链路预测算法,并以真实的世界网络进行了实证分析,结果表明新的算法比其他算法速度更快,而且精度更高.总之,学者们提出了诸多方法去解决链路预测问题,这些方法主要以测量节点之间相似性为基础.其中目前应用最广泛的测量方法、即相似性预测算法有结构等价指标CN、资源分配指标RA、约旦系数指标JC和阿达米克—亚达指标AA[32-34].
但是,以上的研究较少涉及到产业网络的链路预测问题,并且随着时间的演化,产业网络中原有的链路可能消失或产生新的链路.相似性链路预测算法,虽然可以根据当前的产业网络,预测任意两个产业将来发生链接的概率.但是,产业网络的拓扑结构随时间而变化,产生了大量涉及节点和链路的动态信息,若能在链路预测的算法当中体现出这些有用信息,则预测的精度会有进一步的提高.为了检验这个设想,本文以中国2005年、2007年、2010年和2012年的四个投入产出表为研究对象,首先构建四个有权重的产业网络,然后基于权重网络提出一种新的链路预测算法,建立基于链路动态变化的产业网络预测得分算法,识别两个产业之间建立链接的可能性大小.与相似性预测算法相比,这种新的算法不仅考虑两个节点之间的相似性程度,受到共同邻居节点的影响(本文用控制变量α表示),而且考虑在前期网络和当前网络中,链路权重的变化程度(本文用变化率r表示).在考虑了变化程度的基础上,又进一步考虑了链路权重变化的方向,即权重的增减情况(本文分别用三个参数δ,η,θ表示).此外,为了测试本文提出的预测算法性能优劣,又进一步引入了目前应用最广泛的相似性链路预测算法作为对比,结果显示本文提出的链路预测模型的预测精度更高.因此,在预测产业网络的链路时,不仅要考虑当前产业网络的链路情况,还要充分考虑产业网络中链路的动态变化信息,这样得出的结果才会更加准确可靠.
2 基于链路动态变化的产业网络预测模型
产业网络具有动态的演化结构,这些结构随时间的演化而变化,新的节点不断产生,新的链路不断形成,以及其上的权重不断改变,使得产业网络结构具有动态性.针对产业网络中链路动态变化的特性,并考虑到两个节点邻居的得分情况,本文提出的预测算法,在权重的特定比例上定义预测得分的增加或减少.
2.1 产业网络模型的构建
本文旨在研究产业网络中的链路预测方法,因此,首先讨论如何构建产业网络,而投入产出表是构建产业网络的基础,且能准确表达各个产业部门在生产与分配领域的经济联系.本文分析的投入产出表,是以直接消耗系数为元素所构成的矩阵.记A=(aij)n×n为直接消耗系数矩阵,其中aij,i,j=1,2,...,n为直接消耗系数,且aij∈[0,1].直接消耗系数反映了产业部门生产一个单位的总产品所需要消耗其他部门产品的比例,它是一个无量纲的数值,恒在[0,1]区间变化,因此不会发生随着经济的增长其绝对值随之增加的情况,并且本文是根据历年的投入产出情况,预测任意两个产业部门之间未来的链接情况,而直接消耗系数既可以反映两个部门之间有无联系,又可以反映出联系的紧密程度,其比值越接近于1,联系越紧密;反之越稀疏.以直接消耗系数为链路,产业为节点构建的产业网络考虑的是任意两个产业部门之间的链接情况,与方向无关,因此本文研究无向网络.同时,考虑到链接的重要性,借鉴刘刚等[6]的处理方法,仅将两链接量作均值处理,再将所有产业对链接量的均值设为阈值,阈值以上的值定为有效链接.
2.2 产业网络的结构指标
1)平均度
网络的平均度定义为节点度数中心性的平均值,节点i的度数中心性表示与其相连边的个数ki,其表达式为

其中Γ表示与节点i直接相连的节点组成的集合,亦称为节点i的邻居节点集.eij=1时表示节点i与j存在连边,否则eij=0.度数中心性ki越大,表示产业部门i在产业网络中与产业部门的联系就越多,在相应的投入产出表中作用就越重要,与其它产业部门进行的物质、副产品和能量的交互往来就越多.
2)密度
网络的密度ρ反映网络节点间联系的紧密程度,表达式定义为

其中L为网络中实际存在的有效关联数,N为网络中所有产业部门的个数.ρ越大,表示在相应的投入产出表中,产业部门间的联系越紧密.
3)簇系数
在网络中,网络的簇系数是所有节点簇系数的均值,而节点的簇系数定义为

其中ei表示节点i的邻居节点之间实际存在的边的个数,ki表示节点i的度数中心性.
网络的簇系数表示的内涵是,你的朋友圈或熟人圈中的每个人都是相互认识的.事实上,因为你的朋友大部分是你的同事、同学和邻居,所以他们互相认识的概率自然应该很大.
4)平均最短距离
平均最短距离d是网络的一个重要结构指标,网络中所有节点之间的平均最短距离定义为

其中N为网络中所有节点的个数,dij为连接节点i和j最短路径上的边的个数.
网络中的搜索、路由等相关算法的高效实现皆与平均最短距离紧密相关.在相应的投入产出表中,平均最短距离越小,表示任意两个产业部门之间的物质、副产品和能量的流动就越便捷.
2.3 演化情形
本文定义产业网络中链路动态变化,为网络中任意两个节点之间物质流从一种状态到随后另一种状态的变化情况.观察历年的产业网络可以发现,节点之间的权重有衰减、保持不变和增加三种情形.由于节点对(u,v)之间的权重ω(u,v)往往随着时间的变化而变化,因此可用ω(u,v,t),t∈[0,∞)表示网络中节点对(u,v)之间的权重ω(u,v)是时间t的函数.在产业网络中,任意一对节点之间的权重增减数值各不相同,为了便于定义随后的预测得分,本文引进变化率r(0<r<1),基于任一t1时刻的产业网络中任意一对节点(u,v)之间的权重ω(u,v,t1)(0),定义三个集合E1=[0,(1-r)ω(u,v,t1)),E2=[(1-r)ω(u,v,t1),(1+r)ω(u,v,t1)),E3=[((1+r)ω(u,v,t1),∞),显然然后,视权重ω(u,v,t),t>t1与三个集合的隶属关系,把权重的演化情况分别分为衰减、保持不变和增加三种类型.
1)衰减
当产业网络从t1时刻的状态演化到t时刻的状态时,若节点对(u,v)之间的权重ω(u,v,t)较权重ω(u,v,t1)为减少,且ω(u,v,t)∈E1时,定义此时的衰减函数为
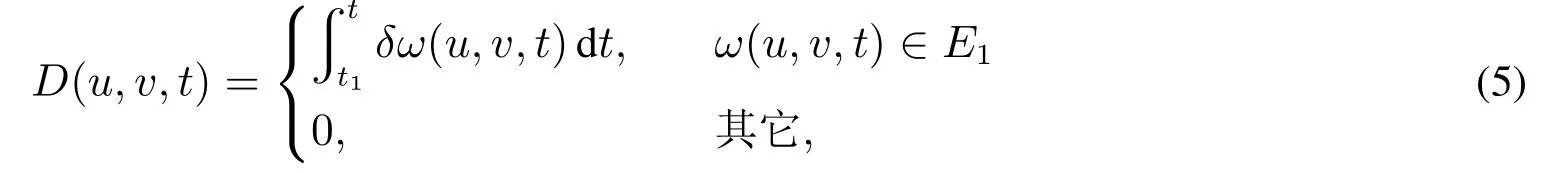
其中δ为负数,表示权重在衰减.
由于节点对之间的权重从t1时刻的状态演化到t时刻的状态时,其变化过程中权重是连续变化的,因此衰减函数可用积分表示.
2)保持不变
当产业网络从t1时刻的状态演化到t时刻的状态时,若节点对(u,v)之间的权重ω(u,v,t)较权重ω(u,v,t1)变化不大,即ω(u,v,t)∈E2时,定义此时的不变函数为
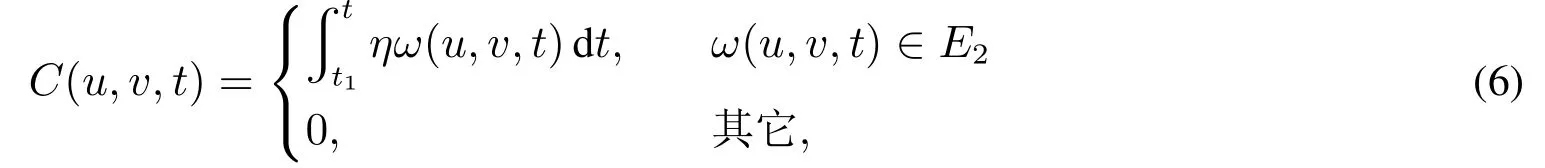
其中η为非负数,表示权重的变化细微,可以忽略不计.
3)增加
当产业网络从t1时刻的状态演化到t时刻的状态时,若节点对(u,v)之间的权重ω(u,v,t)较权重ω(u,v,t1)为增加,且ω(u,v,t)∈E3时,定义此时的增加函数为
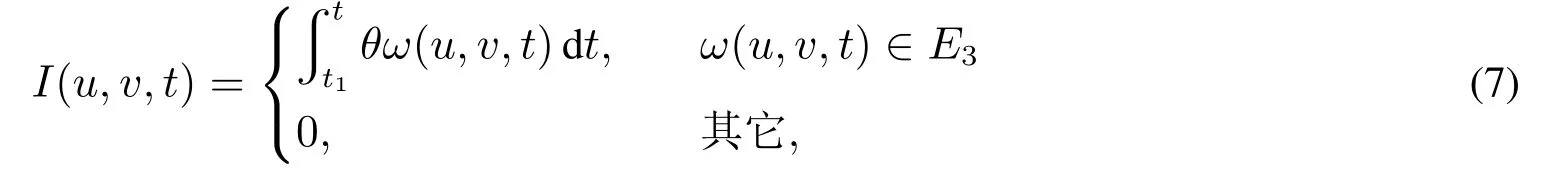
其中θ为非负数,表示权重在增加.
由以上的定义可知,参数θ,δ和η的关系应为θ>η>δ,三者的数值将在评估预测算法的性能时确定,选择预测精度最高的参数值.
2.4 基于链路动态变化的产业网络预测得分
与相似性预测算法不同,本文提出的算法不仅考虑两个节点之间的相似性程度受共同邻居节点的影响,而且考虑前期网络和当前网络中,链路权重的变化程度,在考虑了变化程度的基础上,又进一步考虑链路权重变化的方向,即权重的增减情况,来定义节点对(u,v)在区间[t1,t2],t2>t1上的预测得分score(u,v)为
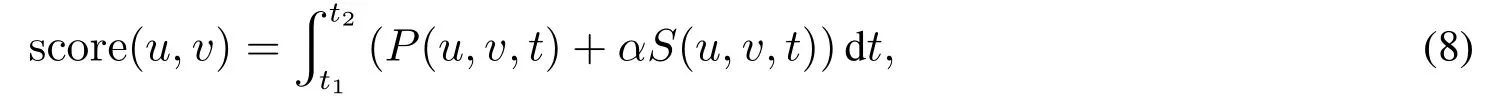
其中P(u,v,t)=D(u,v,t)IE1+C(u,v,t)IE2+I(u,v,t)IE3,S(u,v,t)=+P(y,v,t)],Γ(u)表示节点u的邻居节点的集合,IEi,i=1,2,3是Ei的示性函数.
P(u,v,t)计算了产业网络中节点对(u,v)从t1时刻的状态演化到t时刻的状态时的得分.假定节点y是节点u,v共同的邻居节点,令S(u,v,t)表示分别与节点u,v相邻的节点对(u,y)与(y,v),从t1时刻的状态演化到t时刻的状态时的所有得分之和.参数α是控制变量,表示邻居节点影响到节点u和v之间关系的程度.score(u,v)就是基于链路动态变化的产业网络预测模型的得分计算公式.特别,在ω(u,v,t1)=0的情形下,若ω(u,v,t)=0,则设P(u,v,t)=0;若ω(u,v,t)̸=0,则设P(u,v,t)=θ.由此构建的式(8)包含了两个节点间的相似性程度受共同邻居节点的影响,节点间的链路权重变化程度,以及变化的方向等动态信息,其中利用三个连续区间E1、E2和E3,把投入产出表每五年更新一次,这种离散的跳跃,分别归类到这三个区间,据此构建连续变化性模型,来预测当前产业网络的链接情况.
2.5 模型的预测算法精度实验设计及敏感性分析
2.4节提出的基于链路动态变化的产业网络预测模型,既考虑了两个节点之间的相似性程度受共同邻居节点的影响,又考虑了在前期网络和当前网络中,链路权重的变化程度以及变化的方向.那么该模型的算法精度如何,本文将引入相关指标作进一步分析.目前,共有三种衡量链路预测算法精度的指标,分别为AUC(area under the receiver operation characteristic curve),Precision和Ranking score[35].它们对预测精度衡量的侧重点不同.由于本文以整个产业网络为研究对象,因此使用AUC指标从整体上来衡量算法的精度,并且产业网络是小规模的网络,因此本文在计算AUC时,采用逐项遍历方法,即每次从网络中选取一条边进行测试,余下的边作为训练集,然后测试这条边,得到一个相应的预测精度.最后遍历网络中的每条边,计算平均值,作为整个网络的预测精度.同时,在基于链路动态变化的产业网络预测算法式(8)中,为了得到算法精度最优的参数值,本文将采用正交试验设计[36],及其统计方法确定所需的参数,并分析数值模拟结果对相关参数的敏感性.
3 基于链路动态变化的产业网络预测模型实证分析
本文以中国投入产出表为例,选出2005年、2007年、2010年和2012年的中国投入产出直接消耗系数表作为研究对象,以直接消耗系数为链路,产业部门为节点构建产业网络.由于本文提出的预测算法,主要考虑产业网络中链路动态变化的情况,即在产业网络中保持节点个数不变,考察随着时间的演化,网络中任意两个节点之间链路的断开或链接情况,然后据此预测下一期的产业网络.而在中国历年的投入产出表中,产业部门的名称和数目(网络中的节点)并不是完全一致.因此,本文采用文献[37]的处理方法,只对前后不统一的产业部门,即2005年的旅游业,2007年、2010年、2012年的水利、环境和公共设施管理业,对这两个产业部门进行合并与整理,而其他的产业部门不会改动,因此在删除这两个产业部门后,对其余产业部门之间、产生的新链路或消失的链路影响甚微.鉴于此,把2005年投入产出表中旅游业所在的行与列删除,把2007年、2010年、2012年投入产出表中的水利、环境和公共设施管理业所在的行与列删除.利用前文构建产业网络的方法,得到四个年份的有权重的、且是无向的产业网络,如图1所示,从左到右,从上到下分别是2005年、2007年、2010年和2012年的产业网络.
图1 四个年份的中国产业网络Fig.1 China’s industrial network in four years
利用式(1)~式(4),对各个年份产业网络的结构指标进行分析,得到的结果如表1所示.
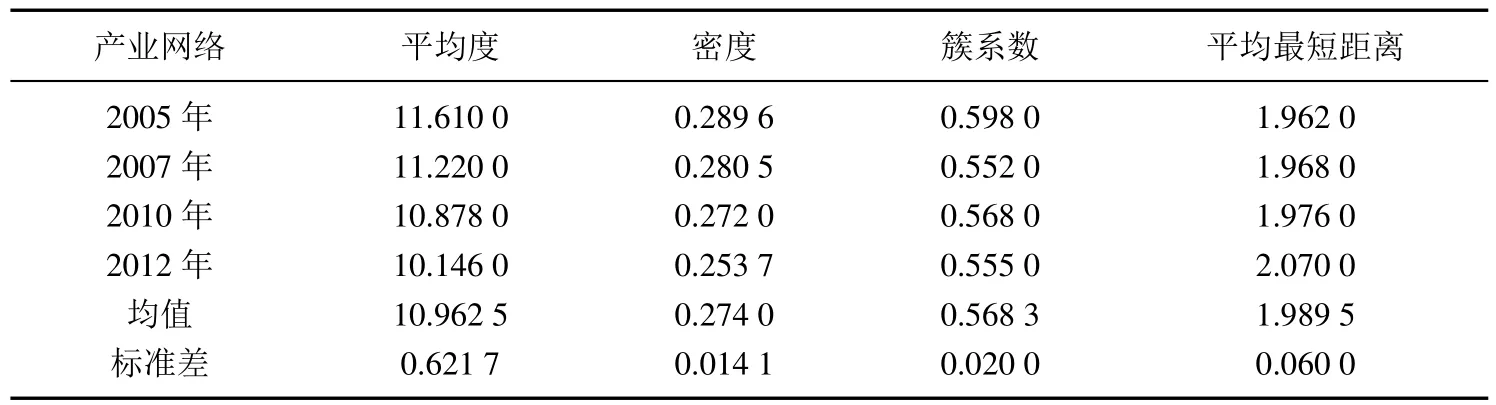
表1 各个年份产业网络的参数Table 1 Parameters of industrial network in each year
由表1可知,平均度和密度逐年减小,平均最短距离逐年增大,而簇系数没有明显的变化规律.结果表明物质、副产品和能量的循环流动可以到达更远的产业部门,资源的利用更加充分,但从数值上看,这种变化又不太显著.四个年份的产业网络的平均度、密度、簇系数和平均最短距离的标准差很小,各项指标相似,说明四个产业网络的结构非常接近,因此可以构建新的链路预测模型.
3.1 产业网络的预测
由于我国投入产出表每五年编制一次,中间年份再出一次延长表,分别于1997年、2002年、2007年和2012年四个年份出版,而2000年、2005年和2010年的表格是投入产出表的延长表.其中2005年以前的投入产出表距本文所预测的2015年投入产出关系已达十多年之久,对于预测结果无显著的影响.因此,本文将用2005年、2007年、2010年和2012年的产业网络,去预测下一年份即2015年产业网络的链接情况.这四个年份的结构指标在上节已做了详细分析,结果非常接近.因此,可以利用基于链路动态变化的产业网络预测模型中的式(8),计算2015年产业网络中任意两个节点之间的得分,再利用2.1节中产业网络模型的构建方法,得到2015年的产业网络.进而,可将2015年产业网络的预测结果、与过去几年的真实数据相比较,分析产业的转型升级、迁移等情况.下面将以产业网络结构指标中的度数中心性为例,分析产业重要性的演化情况.利用式(1),计算预测得到的2015产业网络中各个产业的度数中心性,再与2005年和2010年相比较,结果如表2所示.
从表2可以看出,批发和零售业度数中心性在2005年的网络中居于第九位,2010年网络中上升到第二位,最后来到了2015年网络中的第一位,重要性可见一斑.事实上,批发和零售业是各个产业部门的产品实现价值的重要媒介,是连接商品生产和消费的主要环节.除了批发和零售业以外,化学工业度数中心性的位置也在提升,由2005年的第七位,到2010年的第四位,最后上升到2015年的第二位,可见其在当下产业网络中的重要性.度数中心性发生显著变化的还有金融业,由2005年和2010年的前十位以外进入到2015年的第四位,它在产业网络内度数中心性位置的提升,说明了其是配置社会资源和融通资金作用的源动力,是现在经济生活的命脉和媒介.批发和零售业与金融业属于第三产业,“十二五”规划结束后,第三产业的度数中心性在前十个产业中占到了六席,产业结构优化调整的效应从预测得到的产业网络中得到了充分的体现.为了得到预测方法精度,下节将给出计算预测算法精度的实验设计和敏感性分析.
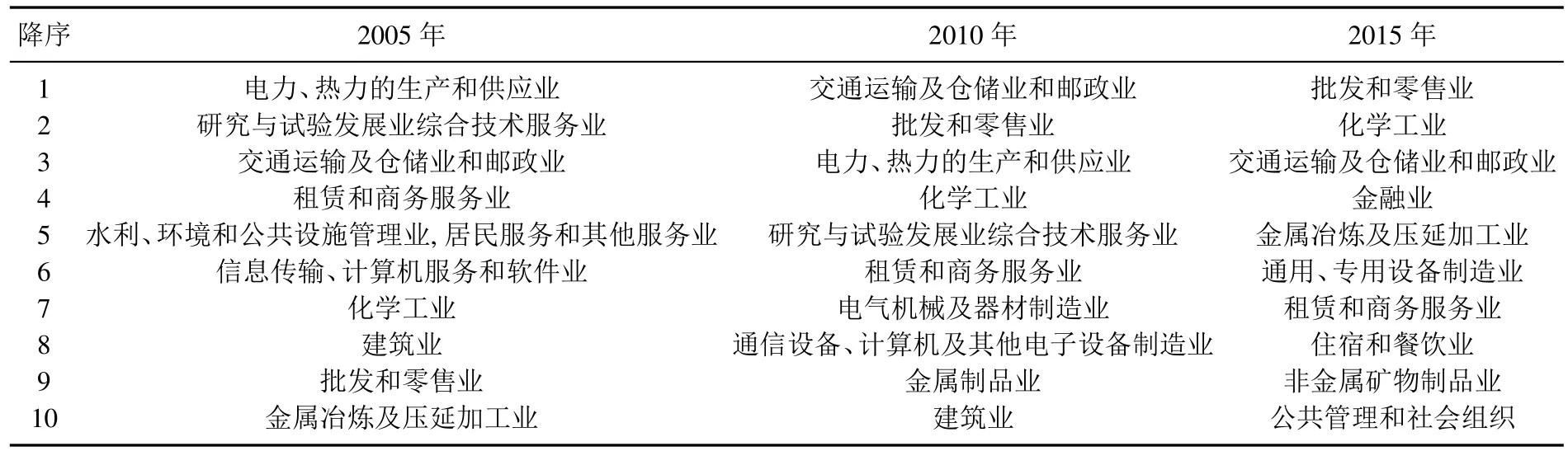
表2 三个年份度数中心性排在前十的产业部门Table 2 Three-year-degree centrality ranked in the top ten of the industry sector
3.2 产业网络预测算法精度实验设计及敏感性分析
实例数据来源于上节所构建的2005年、2007年、2010年和2012年的产业网络,依据预测精度指标AUC,通过正交试验设计和对参数的敏感性分析,给出基于链路动态变化的产业网络预测模型参数的最优设定值.
1)正交试验设计
在基于链路动态变化的产业网络预测算法式(8)中,为了得到算法精度最优的参数值,本文将采用正交试验设计及其统计方法确定所需的参数,并分析参数的敏感性.正交试验设计(orthogonal experimental design)是多因素多水平的实验设计方法[36],依据具体问题选择合适的正交表是使用正交法的关键.在基于链路动态变化的产业网络预测算法中,共有五个参数,依据各个参数所表示的不同意义,r、α和θ分别选取两个水平,δ选取四个水平,η选取五个水平,在此基础上设计正交表.然后,依据正交表进行仿真实验,并将结果列表示意.α的两个水平分别设为0.05和0.1,先分析α=0.05的情况,再分析α=0.1的情况.当α=0.05时,利用网络的两个版本进行研究.一个是基于四个权重产业网络,当变化率r设为25%,另一个变化率r设为50%.计算不同版本下的AUC值并列表显示.当变化率r设为25%,且α=0.05,θ=2时,通过MATLAB 7.0编程计算得到AUC值,如表3所示.当变化率r设为25%,且α=0.05,θ=3时,AUC的值,如表4所示.
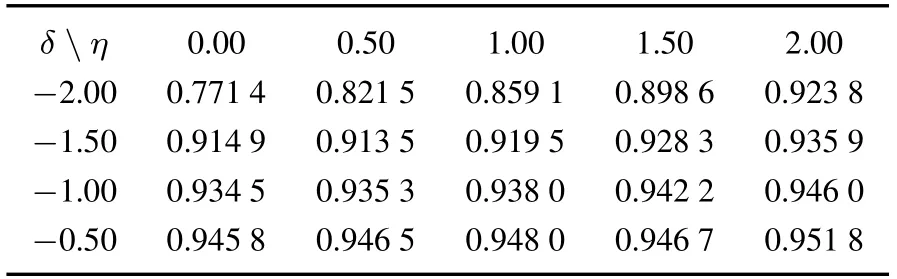
表3 变化率r设为25%时AUC的值(α=0.05,θ=2)Table 3 The AUC values underr=25%(α=0.05,θ=2)
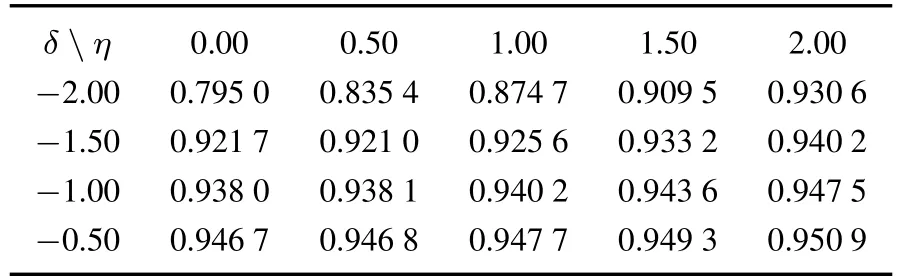
表4 变化率r设为25%时AUC的值(α=0.05,θ=3)Table 4 The AUC values underr=25%(α=0.05,θ=3)
当变化率r设为50%,且α=0.05,θ=2时,AUC的值,如表5所示;当变化率r设为50%,且α=0.05,θ=3时,AUC的值,如表6所示.
从表3~表6可以看出,预测精度AUC最大是表5中的值0.979 3,相应的参数δ,η,θ取值分别为-0.5,0.5,2,同时r=0.5.当α=0.1时,仍然利用产业网络的两个版本进行研究.一个是基于四个权重产业网络,当参数α变化率r设为25%,另一个变化率r设为50%,计算不同版本下的AUC值.计算的方法同α=0.05时的情况,这里就不再赘述.比较分析得到的结果发现,当α,r,δ,η和θ的取值分别为0.05、0.5、-0.5、0.5和2时,预测精度AUC最大.
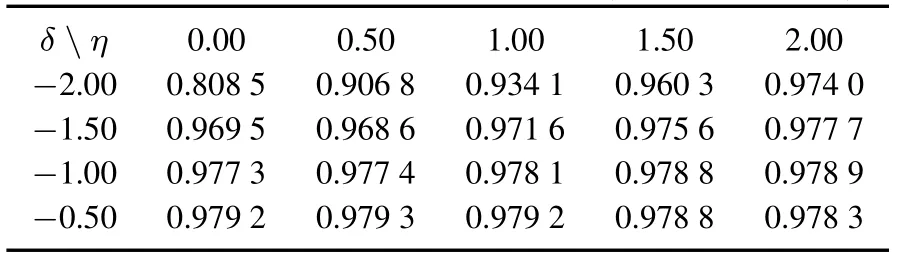
表5 变化率r设为50%时AUC的值(α=0.05,θ=2)Table 5 The AUC values underr=50%(α=0.05,θ=2)
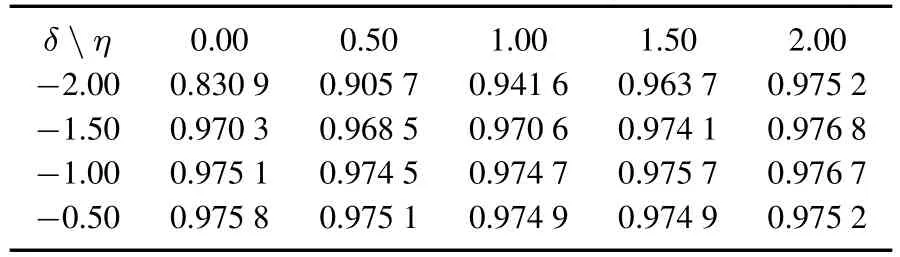
表6 变化率r设为50%时AUC的值(α=0.05,θ=3)Table 6 The AUC values underr=50%(α=0.05,θ=3)
2)参数的敏感性分析
由以上分析的结果可知,当分别以r=0.5和r=0.25,α=0.05和α=0.1,对预测精度AUC进行变化分析时,得到链路预测算法中各个参数α,r,δ,η和θ的取值分别为0.05、0.5、-0.5、0.5和2时,预测精度AUC最大.为了研究数值模拟结果对这两个参数的敏感性,在此做一个敏感性分析,以一定区间的取值范围为参考,考虑r和α对预测精度AUC的变动趋势.不失一般性,r的取值范围为[0.1,0.8],间距设为0.05;α的取值范围为[0,1.5],间距设为0.05,计算其对预测精度AUC的影响,得到趋势图2.当r在[0.1,0.8]范围内取值时,得到预测精度AUC的极差为0.058 3,均值为0.960 3和标准差为0.018 6;而当α在[0,1.5]范围内取值时,得到预测精度AUC的极差为0.161 3,均值为0.867 3和标准差为0.052 8.可见,预测精度对这些参数的变化不很敏感,但α比r的敏感性要高,说明在计算预测精度时,优先考虑到两个节点的关系受到邻居节点的影响程度.
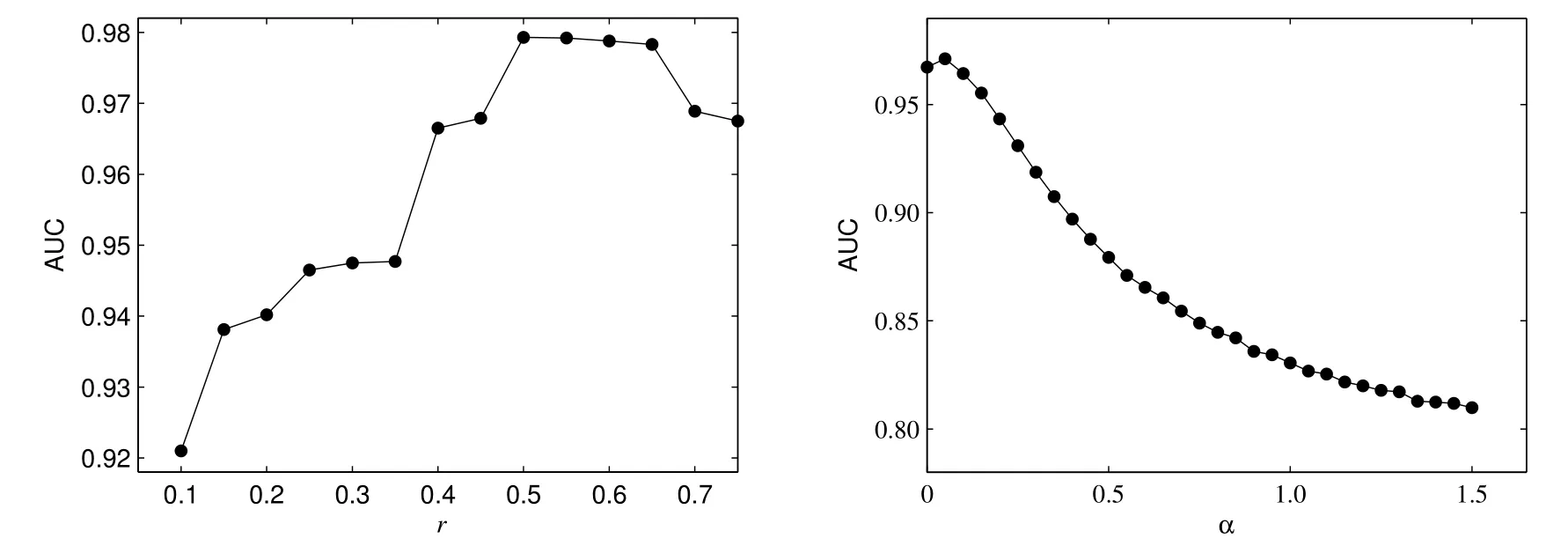
图2 AUC的变化趋势Fig.2 The change trend of AUC values
3.3 预测算法精度的对比分析
为了测试本文提出的预测算法性能的优劣,进一步引入相似性链路预测算法作为对比.相似性链路预测算法指标有两类,一类是基于无权网络的相似性指标,如式(9)~式(12)所示;另一类是基于权重网络的指标,如式(13)~式(16)所示.它们分别为CN指标(common neighbors,又称结构等价指标)、RA指标(resource allocation指标,资源分配指标)、JC指标(Jaccard’s coefficident指标,约旦系数指标)和AA指标(Adamic-Adar指标,阿达米克-亚达指标)[32-34].这八个指标的具体表示式为
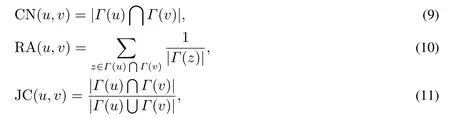
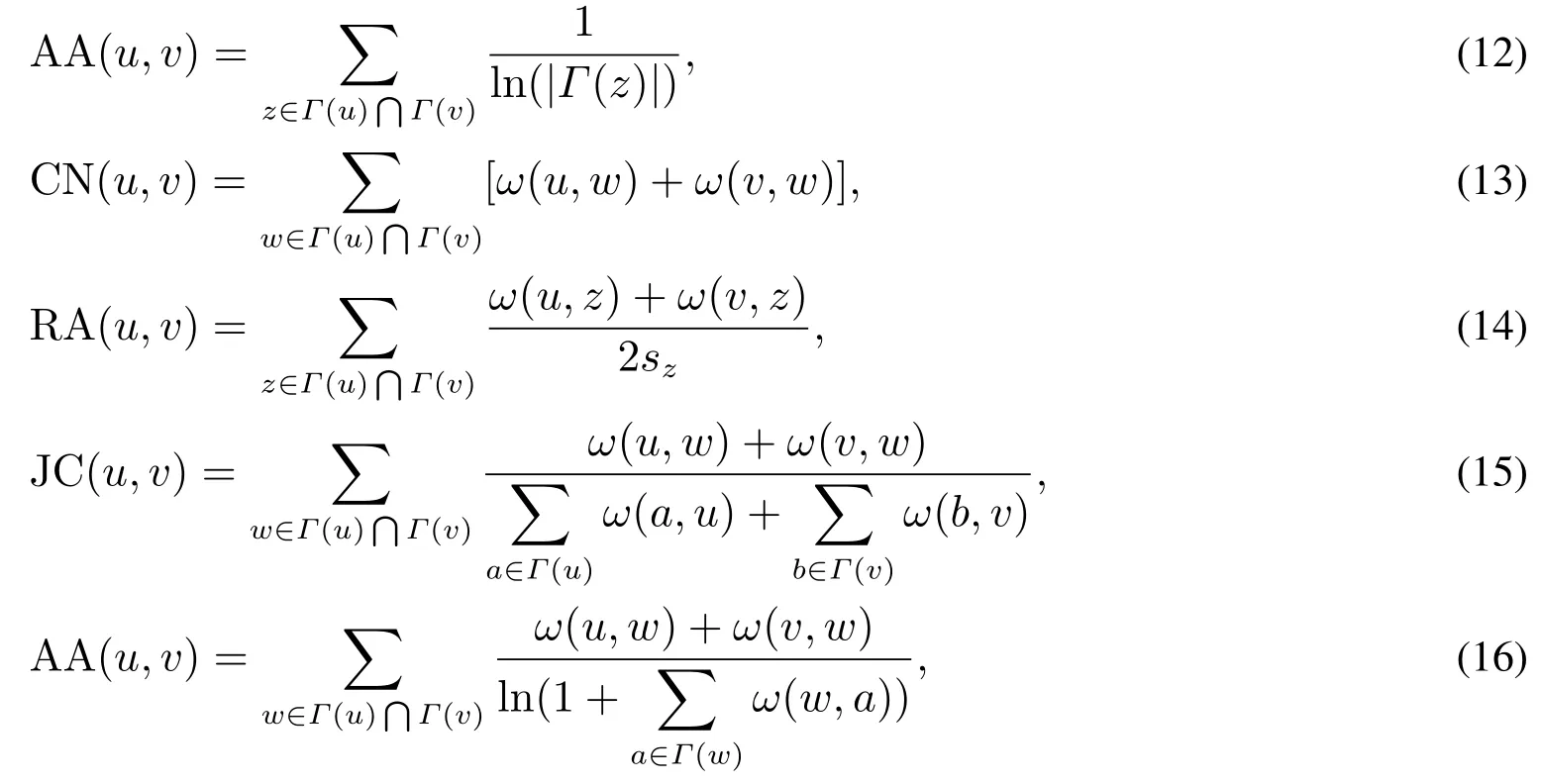
其中Γ(u)和Γ(v)分别表示节点u和v的邻居节点的集合,|Γ(z)|表示节点z的度,sz表示节点z的强度.
在文献[32—34]中,没有考虑节点u,v之间的权重ω(u,v)与时间的关系,因此式(13)~式(16)中只利用ω(u,v)表示节点u,v之间的权重,而本文提出的预测模型中考虑了节点u,v之间的权重ω(u,v,t)与时间相关,并据此提出了基于链路动态变化的产业网络预测模型.许小可等[38]研究发现,如果任意两节点之间的最短距离长度大于等于2时,那么可以使用以上基于共同邻居算法的八种链路预测算法.由于在2005年、2007年、2010年和2012年的产业网络中,任意两节点之间的最短距离长度大于等于2,因此,可以使用相似性链路预测算法作比较.
截至目前,由于2015年包含42部门的投入产出表,尚未对外公布,因此无法分析2015年产业网络的真实情况.因此本文采用链路预测中的常用做法,再结合本文研究的产业网络的特征,利用2.5节中所介绍的预测精度指标AUC,去衡量本文算法与相似性链路预测算法哪个更加优越.现将相似性链路预测算法的精度AUC,计算得到的结果,列于表7.

表7 相似性链路预测算法的精度AUCTable 7 The AUC values of prediction accuracy based on similarity link prediction algorithm
其中AUC的最大值为0.840 8,而基于链路动态变化的产业网络链路预测算法的精度为0.979 3.与相似性链路预测算法的精度相比较,显然本文算法的预测精度最大.因此在预测产业网络的链路时,不仅要考虑产业网络当前的链接情况,还要充分考虑产业网络的演化情况,这样得出的结果才会更加准确可靠.
4 结束语
当考虑了产业网络的链路动态变化因素时,通过对中国2005年、2007年、2010年和2012年产业网络的拓扑结构及链路权重变化的分析,提出了一种新的产业网络预测算法模型.新的预测算法不仅考虑了产业网络中链路的动态变化信息,而且考虑到两个节点邻居的得分情况,在权重的特定比例上定义预测得分的增加或减少,最后把每个变化过程的得分相加即得产业网络的链路预测得分.实证结果表明,利用正交实验设计方法,只要其中的参数选取合适,则新的产业网络预测算法模型具有理想的预测精度.并且相比于相似性链路预测算法,本文提出的基于链路动态变化的产业网络预测模型的预测精度更加理想.因此链路上的动态变化信息对预测产业网络具有重要意义.
为使产业网络的预测更加准确,研究者们应该充分考虑过往信息对产业网络链路预测的重要性.由于数据的易得性,本文仅仅考虑了中国产业网络的演化情况.其实,产业网络(产业共生网络)形态各异,既有宏观上的产业网络,又有中观或微观上的产业网络,深入研究这些网络的链路预测很有意义,可以指导产业的升级或迁移等问题.在将来的工作中,将更加注重这方面的研究.

