基于SIMPACK和Simulink联合仿真的摆式车辆曲线通过研究

胡骁樯， 倪文波， 王雪梅， 曲文强

(1 西南交通大学 机械工程学院， 成都 610031；2 中车青岛四方机车车辆股份有限公司 国家工程研究中心， 山东青岛 266111)

自1997年以来，我国铁路进行了6次大提速，并开行了2万km多的高速铁路。高铁的快速发展为人们的出行带来便利，产生了巨大的社会效益，但全国仍然有12万km多的既有线铁路，线路等级低，尤其在山区的铁路曲线半径小，限制了列车运行速度的提高。国外的研究及实际运行状况表明，摆式列车可以在对线路作出相对较小的改造下显著提高既有线列车的运行速度[1-3]。摆式列车的优势在于以高于普通列车的速度通过小半径曲线，仍然保证旅客乘坐舒适度，并且线路改造投资小，提速效果显著[4-5]。摆式列车发展至今，国外的摆式技术越来越成熟，在多个国家得到很好的应用。波兰国家铁路公司PKP于2011年5月30日向阿尔斯通公司订购了20列ETR610摆式列车并于2013年交付第一列[6]。可以看出，摆式列车目前仍然有一定的市场需求，不断有新的车型出现。

尽管从上世纪90年代开始，国内的学者对摆式列车进行了大量的研究[7-11]，但种种原因导致摆式列车在中国至今没有得到实际应用。继续对摆式列车曲线通过时的性能进行研究，可为将来车辆的顺利研发提供技术储备。随着计算机仿真技术的发展，采用SIMPACK软件建立的车辆动力学模型已经在铁道车辆开发中得到了很好的运用。进一步采用MATLAB软件建立倾摆控制系统的模型，采用联合仿真的软件技术，将能够对车辆在通过曲线时列车的实际运行状态进行分析。因此本文将在介绍摆式列车转向架结构的基础上，建立车辆的SIMPACK模型与倾摆作动系统Simulink模型的联合仿真模型，研究倾摆作动系统对摆式列车运行性能的影响。

1 摆式转向架结构

与传统车辆转向架不同，除了轮对轴箱装置、一系悬挂、构架、二系悬挂、抗蛇行减振器、抗侧滚扭杆等部件外，摆式列车的转向架构架与车体之间增加了摆枕、吊杆和倾摆作动器。摆枕通过呈八字形对称布置的4根吊杆安装在转向架的构架上，车体通过空气弹簧坐落在摆枕上，它们共同构成四连杆机构。摆枕和构架之间安装有车体倾摆作动器，倾摆作动器产生伸缩运动，使摆枕通过四连杆机构开始倾摆，继而带动车体产生倾摆。具体结构如图1所示。

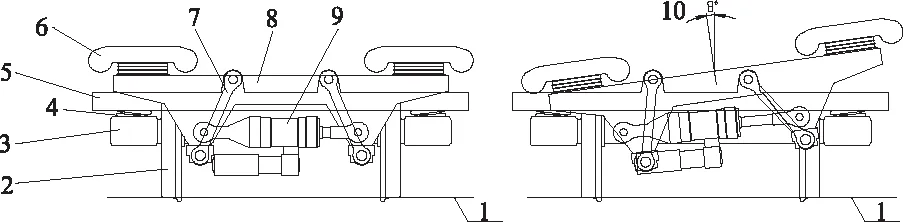
1-轨面；2-轮对；3-轴箱；4-一系悬挂；5-构架；6-空气弹簧；7-吊杆；8-摆枕；9-倾摆作动器；10-向左倾摆8°。图1 转向架结构图

2 倾摆作动系统

摆式列车的倾摆作动系统由机电式作动器和控制计算机组成，核心部件是机电式作动器，其具有体积小、质量轻、可控性好、集成度高等优点。其结构如图2所示。

安装在转向架上的加速度传感器将未平衡加速度信号传递给控制计算机；控制计算机给伺服驱动器发出控制指令，驱动伺服电机旋转；伺服电机经过传动比为12.5的二级齿轮减速后带动螺母旋转，滚珠丝杆机构将电机的旋转运动转变为丝杆的直线运动，从而使作动器产生伸缩运动，借助四连杆机构实现车体倾摆；通过位移传感器的反馈信息完成车体倾摆角度的伺服控制。倾摆作动系统原理如图3所示。

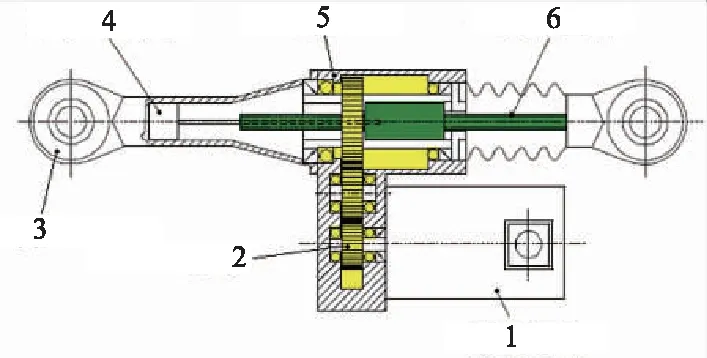
1-伺服电机；2-齿轮；3-铰座；4-位移传感器；5-机体；6-滚珠丝杆。图2 机电式作动器结构图

根据对四连杆机构进行受力分析及运动分析，可得出作动器的最大输出力约为80 kN，在车体倾摆8°时作动器的最大行程为±153 mm，且作动器的位移与车体倾摆角度呈线性关系，从而可将车体倾摆角度值转化为作动器位移值，便于测量与伺服控制[12]。据此选择直径为63 mm、导程为10 mm的丝杆。根据倾摆作动系统的性能要求，将丝杆的运动速度设为80 mm/s。选用伺服电机MDD093C-N-060，其额定扭矩19.5 N·m，额定转速为6 000 r/min。

图3 倾摆作动系统原理图

控制计算机采用PID控制策略[13-17]；伺服驱动器和机械传动部分可看作比例环节；丝杆螺母看作积分环节。建立如图4所示的倾摆系统方框图。

图4中，K1为PID控制器比例系数，K2为伺服驱动器系数，L为丝杆的导程，i为齿轮箱减速比，KE为电机感应电压常数，Tm为电机时间常数，Kf为位移反馈系数，s为拉普拉斯常数。

在MATLAB软件中建立倾摆系统的Simulink数学仿真模型，进行闭环性能测试。给系统施加单位阶跃信号和梯形信号，观察系统的跟随响应特性，仿真结果如图5所示。

图4 倾摆系统方框图

从图5可以看出，单位阶跃信号的响应延迟时间为0.2 s，梯形信号的滞后时间非常小，表明该机电式作动系统响应迅速，动态跟随性好，满足车体倾摆动作的要求。

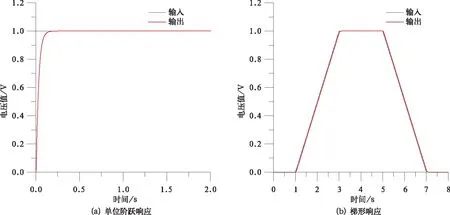
图5 系统跟随响应

3 摆式车辆的动力学模型

在建立车辆模型时，将摆式车辆系统中除弹性元件外的各个部分如车体、构架、摆枕、吊杆、轴箱和轮对等都视为刚体；考虑轮轨接触几何关系非线性、轮轨蠕滑非线性和悬挂非线性，运用多体动力学软件SIMPACK建立摆式车辆的动力学模型，如图6所示。

根据文献[7]，摆枕的自由度可以去掉，将吊杆和作动器的影响归结到倾摆机构对车体重心和摆心的影响上。因此拖车转向架共有34个独立自由度，如表1所示。

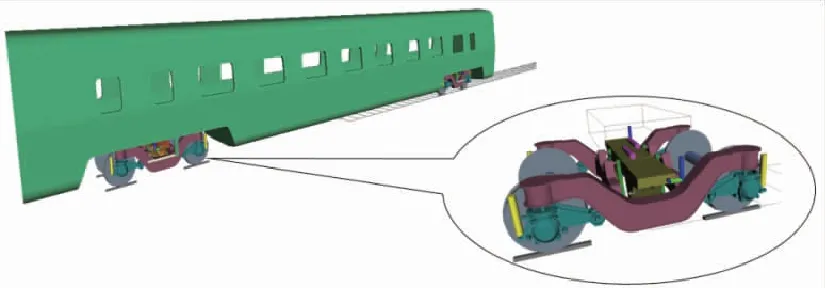
图6 摆式车辆动力学模型

伸缩横移浮沉侧滚点头摇头自旋扰动备注车体XcYcZcθcφcψc--构架XbiYbiZbiθbiφbiψbi-i=1,2轮对XwiYwi---ψwiβwii=1～4

根据表1建立摆式车辆的动力学模型，车体的动力学方程为

(2)

式中，mc为车体质量；Ici(i=x,y,z)为车体绕x，y，z轴的转动惯量；Xc、Yc、Zc为分别为车体的纵向、横向、垂向位移；θc、φc、ψc分别为车体的侧滚角、点头角、摇头；∑Fci、∑Mci(i=x,y,z)为车体外载荷项。

构架和轮对的动力学方程形式与车体相似，可以参考文献[8]，在此不再赘述。

4 联合仿真分析

多体动力学仿真可以实现模型非线性化，较全面地反映整车动态特性。应用SIMPACK和MATLAB软件分别建立摆式车辆的动力学模型和倾摆作动系统数学模型，可以发挥各自的优点，计算精度较高。调用Simulink模块库中的simat模块建立数据交换的通道，将Simulink中的倾摆控制信号通过simat传递给SIMPACK中的动力学模型，使车体产生倾摆，在SIMPACK动力学模型中设置位移传感器，将信号反馈给Simulink控制模型，进行伺服控制，从而建立整个系统的联合仿真模型，如图7所示。

为了研究倾摆作动系统对摆式车辆曲线通过性能的影响，根据不同的线路曲线半径设置了不同的超高和缓和曲线，具体的线路条件如表2所示。线路设置时参考《铁路线路设计规范》，在较好线路上运行的车辆，未平衡离心加速度需小于0.05g(g为重力加速度)，也即欠超高需小于75 mm，为安全起见，本计算各线路最大欠超高均取75 mm。在保证未平衡加速度相同的条件下，按倾摆0°、倾摆3°和倾摆6.5° 3种工况分别进行联合仿真分析，得到在相同欠超高值时3种工况在不同线路条件下的最大通过速度，如表3所示。

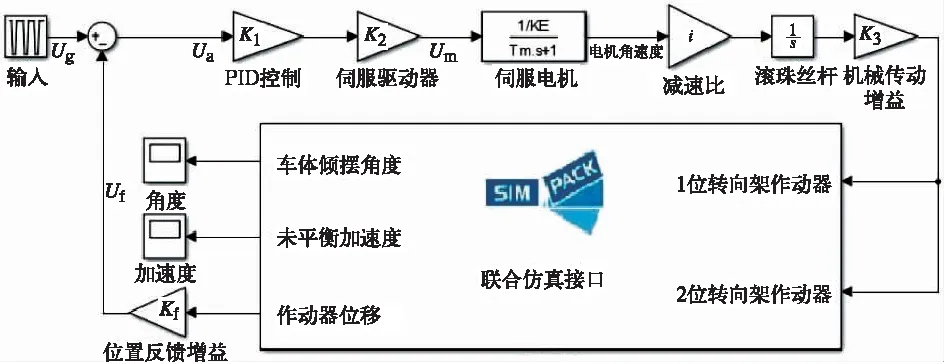
图7 联合仿真模型

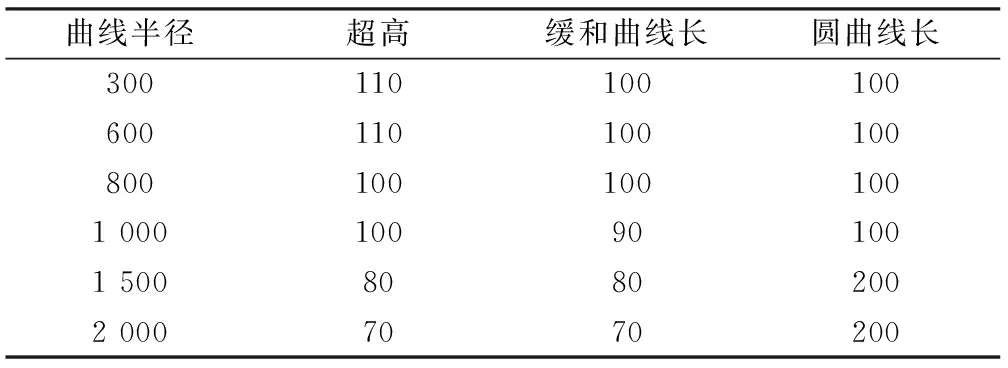
m

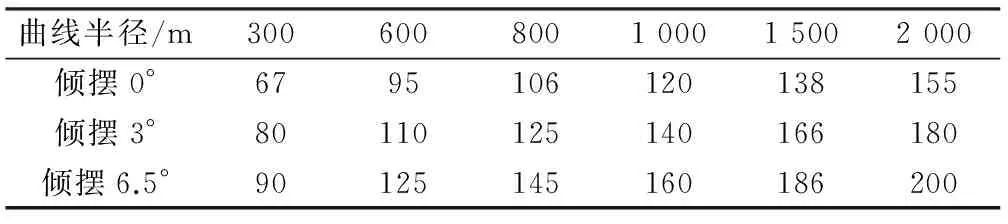
表3 曲线最大通过速度 km·h-1

车辆从直线进入曲线时，在直缓点开始倾摆，到缓圆点时倾摆到所需角度，并在圆曲线上保持倾摆角度不变，出曲线时，在圆缓点开始回摆，直到缓直点回复到无摆角状态。

根据GB 5599-85规定，摆式车辆通过曲线时的动力学评价指标包括：

(1) 轮轨横向力Q

按车辆通过时对线路的影响，轮轨横向力Q允许限度采用以下标准：

Q≤19+0.3Pst

(3)

式中Pst为车轮平均静载荷，kN。

转向架轴质量为15.5 t，则Q=41.79 kN。

(2) 轮轴横向力H

最大轮轴横向力H按以下标准评定：

(4)

式中Pst1、Pst2分别为车轮左轮、右轮静载荷，kN。

转向架轴质量为15.5 t，则H=77.31 kN。

(3) 脱轨系数Q/P、轮重减载率△P/P和倾覆系数D的限度值如表4所示。

摆式车辆在3种倾摆角度下进行联合仿真，线路上施加美国五级轨道谱激扰，保证乘客的乘坐舒适度相同，即乘客的未平衡加速度均为0.05g，按表4中的速度通过曲线，分析摆式车辆的动力学性能。

由图8可知，在相同的线路条件下，随着摆式车辆的倾摆角度增大，各项动力学性能指标也相应增大，但都在标准允许的范围内，而相应的曲线通过速度却可得到提高；在倾摆角度一定的条件下，随着曲线半径的减小，各项动力学指标均增大，并且在小半径曲线上轮轨磨耗更加严重，甚至出现轮缘磨耗，这可能是由于列车在倾摆过程中重心向曲线内侧偏移，加剧了轮轨磨耗。

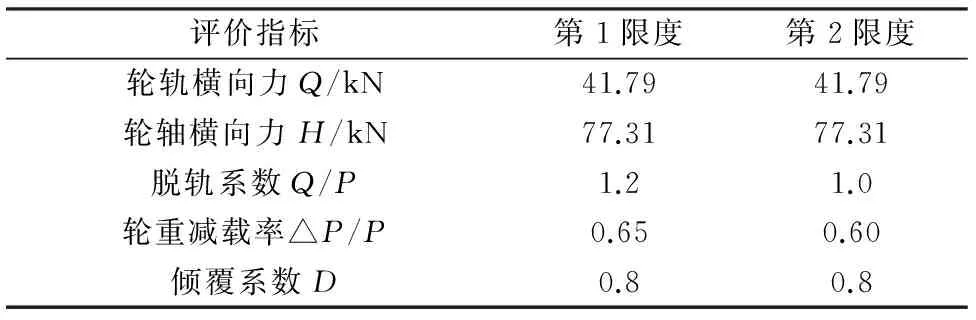
表4 评价指标限度值

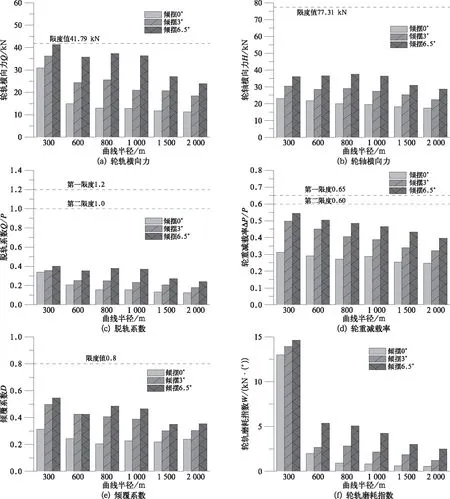
图8 曲线通过动力学性能分析结果

5 结 论

建立了摆式车辆的SIMPACK动力学模型和Simulink倾摆控制模型，采用联合仿真的方法对摆式车辆在曲线运行时的性能进行了分析。结果表明，采用摆式车辆可以在满足乘坐舒适度的情况下提高曲线通过速度，并且各项动力学指标均满足标准要求，进而提高列车的旅行速度。因此，发展摆式列车是提高既有线列车旅行速度的有效途径。

[1] 冯奕续. 摆式列车与铁路既有线提速[J]. 铁道运输与经济, 2003, 25(6): 23-24.

[2] 李芾, 付茂海, 倪文波. 摆式列车及其在中国的运用前景[J]. 学术动态, 2004(3): 1-3,37.

[3] 吴庆杰. 摆式列车重新登上中国铁路发展舞台的探究 [J]. 中国科技财富, 2011(22):245.

[4] 陈文豪. 摆式列车在铁路曲线运行的优势[J]. 路基工程, 2008(4): 22-23.

[5] Rickard Persson, Roger M, Goodall, KIMIAKI sasaki. Carbody tilting - technologies and benefits [J]. Vehicle System Dynamics, 2009, 47(8): 949-981.

[6] Wikipedia. Pendolino[EB/OL]. (2017-04-09)[2017-05-04]. https:∥en.wikipedia.org/wiki/Pendolino.

[7] 周和超, 梁寒冰. 基于Adams与MATLAB联合仿真的摆式列车动力学计算[J].铁道机车车辆, 2010, 30(2): 33-37.

[8] 卜继玲. 主动悬挂摆式列车组运行性能的研究[D]. 成都：西南交通大学, 2001.

[9] 刘宏友, 曾京, 邬平波. 摆式客车曲线通过动力学研究[J]. 铁道学报, 2001, 23(5):22-26.

[10] 罗仁, 曾京. 摆式列车主动倾摆控制的数值仿真研究[J]. 铁道学报, 2006, 28(5): 28-34.

[11] 倪文波, 耿标. 摆式列车倾摆控制系统[J]. 西南交通大学学报, 2000, 35(6): 642-646.

[12] 倪文波，王雪梅. 高速列车网络与控制技术[M](第二版). 成都:西南交通大学出版社,2010: 323-324.

[13] Cheli F, Diana G, Resta F. Numerical Model of a Tilting Body Railway Vehicle Compared with Rig and on Track Tests[J]. Vehicle System Dynamics, 2001, 35(6): 417-442.

[14] Zolotas A C, Goodall R M & Halikias G D. New Control Strategies for Tilting Trains[J]. Vehicle System Dynamics, 2002, 37(sup1): 171-182.

[15] Zamzuri H, Zolotas A C & Goodall R M. Intelligent Control Approaches for Tilting Railway Vehicles[J]. Vehicle System Dynamics, 2006, 44: 834-842.

[16] Hairi Zamzuri, Argyrios Zolotas, Goodall R M. Tilt control Design for High-speed Trains: A study on Multi-objective Tuning Approaches[J]. Vehicle System Dynamics, 2008, 46(1): 535-547.

[17] Hassan F, Zolotas A C & Margetts R M. Optimised PID Control for Tilting Trains[J]. Systems Science & Control Engineering, 2017, 5(1): 25-41.