Effects of Sea-Surface Waves and Ocean Spray on Air–Sea Momentum Fluxes
Ting ZHANGand Jinbao SONG∗Ocean College,Zhejiang University,Zhoushan 36000,China
2State Key Laboratory of Satellite Ocean Environment Dynamics,Second Institute of Oceanography,State Oceanic Administration,Hangzhou 310012,China
1.Introduction
The air–sea boundary layer is an interface for the exchange for matter,momentum and energy between the ocean and atmosphere(Wang et al.,2013).Understanding air–sea interactions and oceanic and atmospheric dynamics requires an accurate understanding of the physical processes that occur in the air–sea boundary layer(He and Chen,2011;Li et al.,2013).
Rapid advances in simulation techniques using computers have allowed complex physical processes in the marine atmospheric boundary layer(MABL)to be simulated,but coupled air–sea mechanisms are still not completely understood.Most coupled air–sea mechanisms currently neglect the physical processes induced by waves, such as wind–wave,wave–wave and wave–current interactions.Neglecting the effects of ocean waves causes large errors in simulation results because near-surface ocean waves have a very strong influence on small-scale air–sea exchanges(Gao et al.,2009;Zhao and Xie,2010).It is therefore important to determine how surface-wave effects on the MABL should be parameterized and to develop an appropriate parameterization to use in numerical models(Rutgersson et al.,2001;Liu et al.,2012).
Under normal conditions,air–sea interface stress has two main components;namely,turbulent shear stress and wave-induced stress.For weak winds,fast-moving waves(for which the phase velocity is higher than the wind speed)induce upward momentum fluxes.The momentum is transformed upward when wave-induced stress is dominant.This upward momentum directly influences and modifies the dynamic and turbulent structures in the atmospheric boundary layer above the sea surface,causing jet fl ow to occur near the sea surface(Harris,1966),and causing the stress vector and wind direction to be distinct(Grachev et al.,2003).Many simple MABL models have been developed to investigate the effect of swell on the MABL(Hanley and Belcher,2008;Makin,2008;Semedo et al.,2009).Building on the findings of Hanley and Belcher(2008)and Makin(2008),Song et al.(2015)proposed a modified Ekman model to study the effects of surface waves on steady near-surface wind profiles over the ocean.They assumed that the eddy viscosity coeffi-cient varied linearly with height,and the Coriolis force was considered.To identify the impact of surface waves on wind profiles over the ocean,Song et al.(2015)used two examples and compared the analytical solution with observations made at a tower on the island of Ostergarnsholm in the Baltic Sea.The results showed that surface waves can affect near-surface wind profiles at low to moderate wind speed.
However,discussion on the effects of various wave ages on air–sea momentum fluxes has not been presented clearly in previous studies(Andreas,2004;Kudryavtsev and Makin,2011).Some field and laboratory observational data(Powell et al.,2003;Jarosz et al.,2007)have been processed to show that the drag coefficient cannot increase with increasing wind speed at high wind speeds but reaches a maximum and then decreases as the wind speed increases.To explain this phenomenon,Andreas(2004)proposed an empirical formula describing the contribution of ocean spray to the total sea surface stress and pointed out that spray droplets lead to a reduction in drag coefficient at high wind speed.Since then,many researchers have realized the importance of ocean spray and many sea-spray-generation formulas have been proposed(Andreas,1998;Kudryavtsev,2006;Zhao and Xie,2010).Considering the relationship between spray and sea-surface roughness length,Liu et al.(2012)described the process of air–sea interaction at high wind speeds by parameterizing the sea-surface roughness length with ocean spray.Zhang et al.(2016)proposed a formula for describing the effects of ocean spray on the MABL as stress force based on the empirical formula developed by Andreas(2004).Nevertheless,the detailed physical process of spray production is hard to identify through an empirical spray-generation formula.
In this paper,we investigate the effects of ocean surface waves and spray droplets on air–sea fluxes.Firstly,we introduce wave-induced stress to the model of the MABL in the presence of sea-spray droplets(Kudryavtsev and Makin,2011).Then,the analytical solution is obtained by assuming the viscosity coefficient varies linearly with height.Secondly,we calculate near-surface wind profiles and drag coefficients theoretically for different wave ages using the Joint North Sea Wave Project(JONSWAP)spectrum.The theoretical solutions obtained are compared with the model solutions with wave-induced stress or spray stress neglected.Thirdly,we compare the theoretical solutions with laboratory measurements presented by Donelan et al.(2004)and Troitskaya et al.(2012),and with field observations presented by Powell et al.(2003),to allow the accuracy of the model to be verified.Finally,we draw our conclusions and discuss how the model can be developed further in future work.
2.MABL model
2.1.Momentum conservation equation
In winds approaching hurricane strength,ocean-spray droplets proliferate.According to Kudryavtsev and Makin(2011),sea-spray droplets are torn from the breaking waves and injected into the air flow at the height of the breaking wave crests. Thus,the interactions between ocean-spray droplets and wind-velocity shear are notable.The droplets being torn from breaking-wave crests inject momentum into the air flow.Therefore,the volume source of the momentum,defined as the rate of injection of the momentum of droplets per unit volume,should be introduced in the momentum conservation,which becomes(Kudryavtsev and Makin,2011)
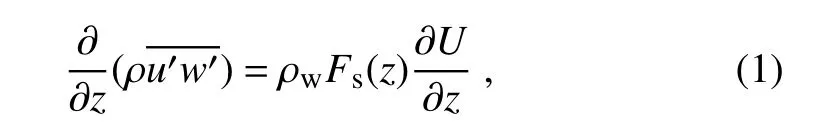
where z is the vertical coordinate,which is the height above the sea-surface roughness lengthis the vertical turbulent fluxes of momentum;U is the mean wind velocity;ρ=ρa(1+σs)is the air-droplet mixture density;σ=(ρw−ρa)/ρais the relative excess of the water density over that of air;ρaand ρware the air and water densities;s≪ 1 is the volume concentration of droplets;and Fs(z)is the droplet flux defined via Vsas

where Vsis the total volume of droplets injected per unit time in unit volume of air and z′is the derivative of variable z.As argued by Kudryavtsev(2006),being torn from breaking wave crests by wind and accelerated to the wind velocity instantaneously,spume droplets are injected into the air fl ow along the mean wind direction.Thus,the effect of spume droplets on the air fl ow mainly concentrates along the mean wind direction.
It is worth noting that winds blowing over the oceans excite the sea-surface waves.These wind waves are responsible for the formulation and regulation of the momentum transfer between the atmosphere and ocean(Gao et al.,2009;Song et al.,2015;Zhang et al.,2016).Herewith,we propose that surface waves extract part of the momentum flux from the total turbulent momentum flux.Based on the assumption that the mean wind and surface wave fields are aligned,we introduce the effect of surface waves into Eq.(1).The momentum conservation equation in consideration of the surface waves and ocean spray can be written as
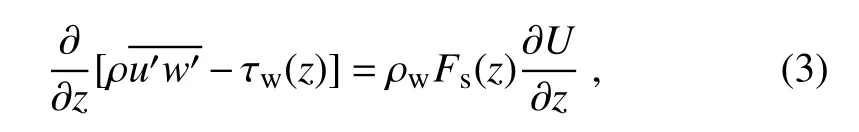
where τw(z)is the wave-induced stress along the wind direction due to the organized waves motions in the atmosphere induced by the waves.If the wave-induced stress is positive[τw(z)> 0],momentum is supplied from the atmosphere to the sea surface;whereas,if the wave-induced stress is negative[τw(z)< 0],the momentum is transferred from the sea surface to the atmosphere(Grachev et al.,2003;Hanley and Belcher,2008;Semedo et al.,2009).
2.2.Closure
Equation(3)indicates that the total momentum flux of turbulence and that induced by waves varies with height.Therefore,we reasonably suppose that the effects of droplets and surface waves on air fl ow dynamics can be neglected well above the sea surface,so that ρ = ρaandwhere u∗is the friction velocity outside the layer affected by the sea-spray droplets and surface waves.Thus,Eq.(3)can be rewritten as


in which the first term describes the redistribution of the momentum between the air and spray droplets and the second term depicts the injection of the droplets’momentum.
The wave-induced stress τw(z)can be estimated by integrating the contributions from waves of all scales(Semedo et al.,2009;Song et al.,2015)using the equation

where ω is the angular frequency in rad s−1,k is the modulus of the horizontal wavenumber vector kkk=(kx,ky)=(kcosθ,ksinθ)given by the dispersion relation ω2=gk for deep water,E(k,θ)is the directional wavenumber spectrum of the surface waves,θ is the direction of the wave vector,and β is the dimensionless rate of growth or decay of a component of the wave spectrum at wavenumber k.
According to the classical closure for turbulent fl ow with suspended particles(Kudryavtsev,2006;Mueller and Veron,2009),turbulent stress can be parameterized as
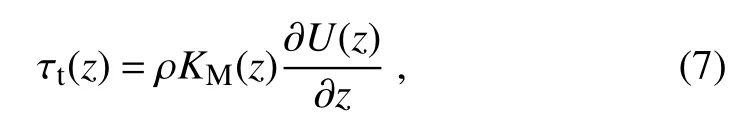
where KM(z)is the vertical eddy viscosity coefficient.
Substituting Eqs.(5)–(7)into Eq.(3),normalized to the density of the mixture in the air,gives the equation

where

The boundary conditions are

and
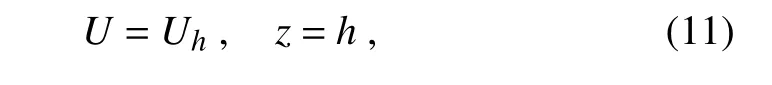
where Uhis the wind speed at the reference level z=h.
3. Solution for eddy viscosity increasing linearly with height
The solutions to Eqs.(8),(10)and(11)can be determined theoretically if the eddy viscosity,wave-induced stress and spray stress are known.Kudryavtsev(2006)argued that ocean-spray droplets influence the strati fi cation of the lower MABL additively.Therefore,he applied Monin–Obukhov similarity theory to the boundary layer strati fi ed due to the presence of sea spray.Thus,the turbulent eddy viscosity reads

where κ=0.4 is von Karman’s constant,LSis the Obukhov length for the turbulent fl ow strati fi ed due to the presence of droplets,and z0is the sea-surface roughness length determined by

which is Charnock’s relation(Charnock,1955).
However,applying Eq.(12)to the theoretical model of the MABL,Kudryavtsev and Makin(2011)pointed out that ocean spray affected the air–sea momentum flux in two ways:by changing the strati fi cation of the lower MABL,and by the effect of spray on the mixture momentum via the spray stress.The latter played such a dominant role that the efficiency of the strati fi cation mechanism could be negligible.Also,Andreas(2004)verified that strati fi cation effects on wind profiles could be negligible,since the residence time of spray droplets in the air fl ow is too short.In addition,sea-surface waves have no effect on atmospheric strati fi cation(Semedo et al.,2009;Song et al.,2015).Thus,without consideration of the effect of spray on strati fi cation,we can define the eddy viscosity increasing linearly with height for neutral strati fi cation as(Xiao and Taylor,2002;Andreas,2004)
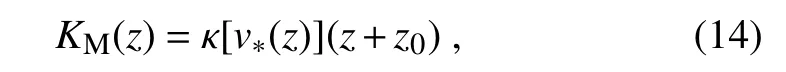
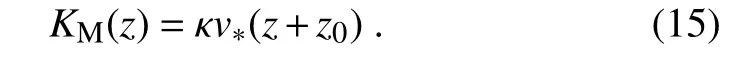
Inserting the KMshown in Eq.(15)into Eq.(8)gives

The general solution to Eq.(16)is

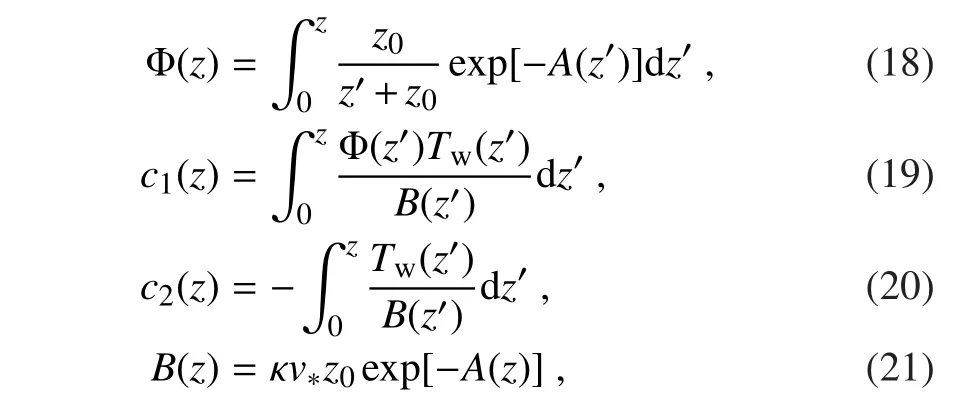
and

It can be concluded from the surface boundary layer condition shown in Eq.(10)thatˆc1=0,and the condition shown in Eq.(11)gives

The solution of Eqs.(8)–(11)is therefore
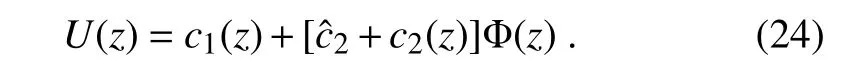
Several interesting special cases can easily be derived from Eq.(24),as follows:
(1)Neglecting the influence of wave-induced stress means that Tw=0 and spray stress and turbulent stress are retained,so the mean wind solution[Eq.(24)]is reduced to
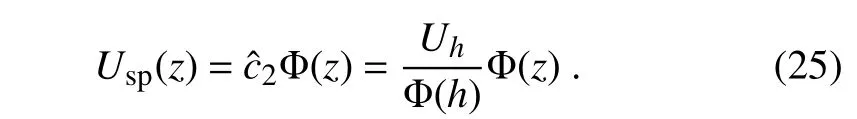
(2)Neglecting the influence of spray stress means that Fs=0 and the effects of wave-induced stress are retained,so the mean wind solution[Eq.(24)]is reduced to
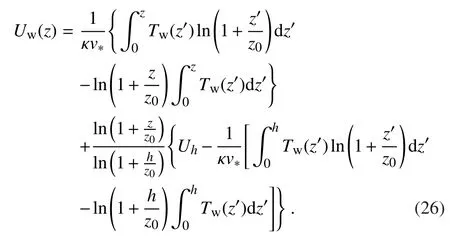
(3)Neglecting both wave-induced stress and spray stress means that Tw=Fs=0,so the wind speed is reduced to a logarithmic velocity profile,

For neutral-stability wind speed considered here,the surface drag coefficient Cd,h(the subscript d is the abbreviation of drag)at z=h(uinits:m)can be estimated using the equation(Makin et al.,1995;Kudryavtsev and Makin,2011)

Using Eqs.(7),(15)and(24)gives
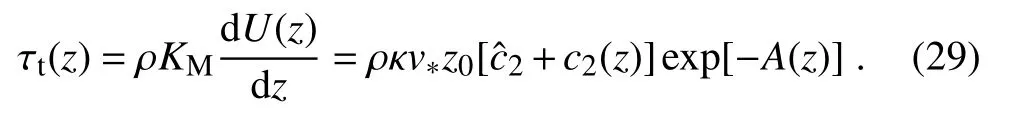

4.Illustrative examples and validation
Several examples are presented in this section to illustrate the effects of surface waves and ocean spray on wind profiles and the drag coefficient in the MABL.As shown by Kudryavtsev and Makin(2011),the volume flux of droplet Fs(z)can be described using the equations

and


where γ is the surface tension,ν is the molecular viscosity coefficient for air,and cris a constant.Here,we use the values kb=5 rad m−1,cr=4.5,cs=1.4×10−5,z=10–100 m,ν=1.46×10−5m2s−1,and γ =7.18×10−2kg s−2.
The behavior of the surface drag coefficient Cd,hand mean wind profiles shown in Eqs.(24)–(27)are investigated using ρa=1.2 kg m−3and ρw=1025 kg m−3and the JONSWAP theoretical directional spectrum(Lucas and Soares,2015):

The constant α used here depends on the significant wave height Hsthrough the equation
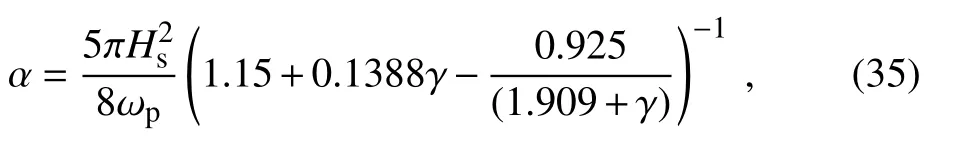
in which,because we investigated sea spectra for different wave ages,the significant wave height uses the 3/2 power lawapplicable to all wind seas(Liu et al.,2012;Zhang et al.,2016),and cp=g/ωp.
As described by Polnikov(2011),the growth rate β is

where cβis a dimensionless function(usually parameterized from various experimental measurements)represented in the form(Polnikov,2011)
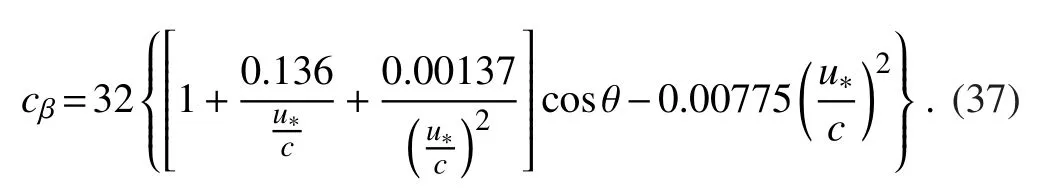
Hara and Belcher(2004)pointed out that the contribution to the wave-induced stress from waves propagating against the wind is negligible because energy in these components is so small.Herewith,Eqs.(6)and(9)can be reduced,respectively,to
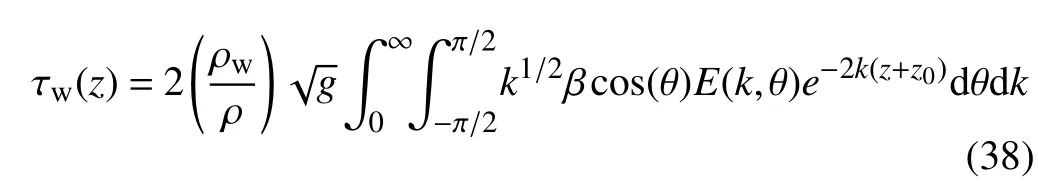
and

For a given Uh,U10and u∗can respectively be calculated using the equations
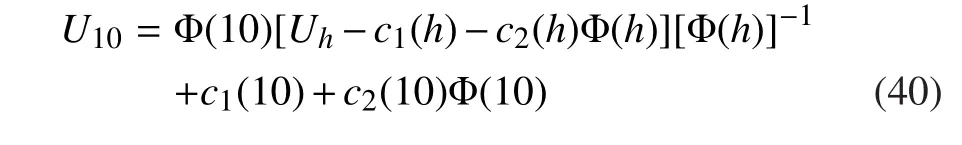
and
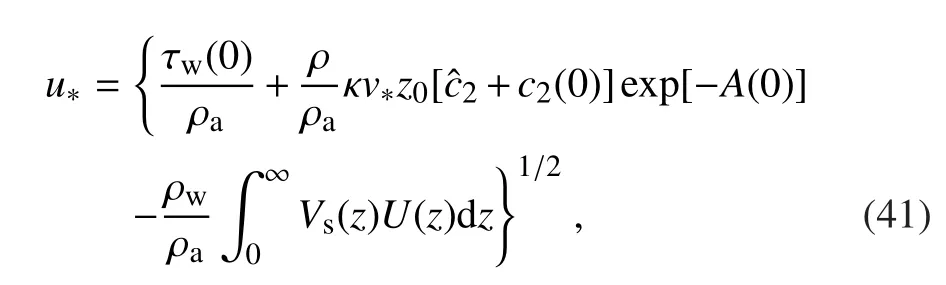
and v∗can be estimated based on the Newton–Raphson iterative technique.Then,the wind profiles Uw(z),Usp(z),U(z)and U0(z),in the lowest 100 m of the MABL,can be calculated after the corresponding friction velocity u∗and local friction velocity v∗become known.
4.1. Mean wind profiles
In this section,the solutions of Eqs.(24)–(27)are calculated for different 100-m wind speeds Uhand four different wave ages(Ω∗=20,25,30,and 40)representing different developmental states of sea-surface waves.The behaviors of the wind profiles Uw(z)/Uh,Usp(z)/Uhand U(z)/Uh,in the lowest 100 m of the MABL,are shown in Figs.1–3,respectively,for wind speeds Uhof 15,25 and 40 m s−1.
Firstly,the effects of surface waves(only)on the near-surface wind speed are investigated.The vertical profiles of Uw(z)/Uhfor four different wave ages with different fixed Uhvalues are shown in Figs.1a–c.Four different wave ages(Ω∗=20,25,30 and 40)that characterize the development of sea waves were used to allow the effects of surface waves on the wind speed at different wave ages to be investigated.A higher wave age corresponds to more mature waves,and in particular,Ω∗≥35 represents fully developed wind waves(Liu et al.,2012).It can be seen from Figs.1a and b that surface waves decrease the wind speed relative to U0/Uhin the lowest 100 m of the whole MABL,only taking surface waves into account at low-to-moderate wind speeds.It can be seen from Fig.1c that surface waves decrease wind distinctly less at a Uhhigher than 30 m s−1.This can be attributed to wave breaking at wind speeds reaching hurricane strength.
Ignoring the effects of surface waves on the wind profiles,the Usp(z)/Uhprofiles from low to high wind speeds can be calculated.The profiles are shown in Fig.2.It is worth noting that the spray stress expression shown in Eq.(5)is not related to the wave age,so the Usp/Uhprofiles can be plotted irrespective of the wave age.It can be seen from Fig.2 that the spray force only accelerates the wind in the lowest 100 m of the MABL at strong Uhrelative to U0/Uh.This is consistent with the conclusion drawn by Kudryavtsev and Makin(2011)that the large amounts of spray droplets torn from breaking waves at high wind speeds cause the wind velocity to increase.However,the effect of spray can be neglected at low and moderate wind speeds,as shown by the overlapping lines in Fig.2.This is because,at such wind speeds,not enough spray droplets are produced to affect the wind speed.The higher the 100-m wind speed,the more ocean spray droplets are produced and the more the wind is accelerated relative to U0/Uh.
The U(z)/Uhand U0(z)/Uhprofiles for different UhandΩ∗,taking both wave-induced stress and spray stress into consideration,are shown in Fig.3.The physical processes of the air–sea interactions can be seen more clearly by inspecting the u∗,v∗,τw(0)/ρaand τsp(0)/ρavalues for different wave ages(Ω∗=20,25,30 and 40),shown in Table 1.

Table 1.Values of u∗,v∗, τw(0)/ρaand τsp(0)/ρafor wave agesΩ∗=cp/u∗of 20,25,30,and 40 for Uh=(a)15,(b)25,and(c)40 m s−1.
As shown in Tables 1a and b,the wave-induced stress values are higher than the spray stress values at low-to-moderate wind speeds,indicating that surface waves affect the MABL more than ocean spray at such wind speeds.The wind profi les shown in Figs.3a and b are similar to the wind profiles shown in Figs.1a and b.Nevertheless,there is a significant difference between Figs.1c and 3c.It can be seen from Tables 1a and b that the u∗values vary less and less as the wave age decreases for a fixed wind speed.This could theoretically be regarded as the reason why the wind speed decreases more for young wave fields than for old wave fields at a given 100-m wind speed,as shown in Figs.3a and b.
Comparing Figs.3a and b shows that surface waves decrease the wind speed at low wind speeds more obviously.At wind speeds Uhexceeding hurricane strength(40 m s−1),the wind speed is stronger compared with U0/Uhin the lowest 100 m of the MABL,as shown in Fig.3c.This is the same as found in Fig.2.The overlapping colored lines in Figs.1c and 3c show that the effects of surface waves on near-surface wind speeds can be neglected.As stated by Kudryavtsev and Makin(2011),spray droplets generated by the wind acting on breaking-wave crests fall back to the sea surface.This accelerates the air fl ow in the spray-generation layer through interactions between the spray droplets and the wind-velocity shear.In turn,this increases the wind speed above the spray-generation layer because of the continuity of the wind velocity.The higher the wind speed,the more spray droplets will be produced and the more clearly the near-surface wind profiles will be affected by ocean spray.Correspondingly,local turbulent stress(v∗)near the sea surface will increase and exceed total stress(u∗),as shown in Table 1c.The increase in local turbulent stress is a consequence of the action of the force required to tear the droplets from breaking crests and accelerate them to the wind velocity.
It can be concluded that both surface waves and ocean spray affect air–sea momentum fluxes,which in turn influence near-sea surface wind profiles.Various wave fields also play a significant role in the air–sea momentum exchanges.
4.2. Sea-surface drag coefficient
As mentioned above,the theoretical model shows that the friction velocity u∗is smaller for young than for mature wave fields at low-to-moderate wind speeds,causing the wind speed to be lower for young wave fields than for old wave fields in the lowest 100 m of the MABL.The theoreti-cal model also indicates that the friction velocity will increase slowly at extremely high wind speeds because of ocean spray,causing near-surface wind to accelerate.Here,in order to compare the theoretical values with the observations,we calculate the drag coefficient Cd10using Eq.(28)for six different wave ages(Ω=0.2,0.3,0.4,0.6,0.8 and 1.2)and compare the results with previous laboratory and field observations.The wave age is herein defined as Ω=cp/U10,similar to the way we define the developmental sea-surface wave field observations Ω∗=cp/u∗.The relationships between the drag coefficient and 10-m wind speeds for different wave ages are shown in Fig.4.The solid lines are the results of using Eq.(28),taking into account the ocean spray and the effects of surface waves at different wave ages,and the dotted lines are the results taking only the effects of ocean spray into account(τw=0,τsp≠ 0).
As shown in Fig.4,the drag coefficients Cd10at low-to moderate wind speeds increase as the wind speed increases,and the Cd10values are lower for young than for old wave fields.The differences between the dotted and solid lines calculated by taking surface waves into account indicate that surface waves decrease the drag coefficient markedly,so surface waves cannot be ignored as they have been in previous studies(Andreas,2004;Kudryavtsev and Makin,2011).
It can be seen from the almost overlapping solid and dotted lines in Fig.4,however,that at high wind speeds the drag coefficient starts to decrease at U10=40 m s−1.This corresponds to the friction velocity increasing more slowly as the wind speed increases[illustrated in Eq.(28)],which is consistent with observations and the theoretical results of several previous studies(Powell et al.,2003;Andreas,2004;Jarosz et al.,2007).This indicates that the effects of surface waves on the drag coefficient are negligible at high wind speeds compared with the effects of ocean spray caused by the wind tearing droplets from breaking waves and suppressing the total momentum in the MABL.As pointed out in Kudryavtsev and Makin(2011),at very high wind speeds,a thin part of the surface layer adjacent to the surface turns into a regime of saturation with spume droplets,resulting in a reduction in the drag coefficient asIt is worth noting from Fig.4a that,the lower the wave age,the higher the wind speed at which the drag coefficient begins to decrease.Spray stress is therefore indispensable in the MABL model,especially at high wind speeds.
Laboratory measurements made by Donelan et al.(2004)and Troitskaya et al.(2012)are shown in Fig.4a to verify the accuracy of the model.Donelan et al.(2004)used a wind–wave tank to examine the wind stress at different wind speeds.The data presented by Troitskaya et al.(2012)were measured using a wind–wave tank with a wind fetch of 7 m.Liu et al.(2012)stated that wind fetch limitations in laboratory experiments mean that the waves,as measured,are younger than waves measured in field experiments.Field data from the Southern Ocean Waves Experiment for low and extreme wind speeds presented by Powell et al.(2003)are shown in Fig.4b to validate the theoretical solutions for old waves.Powell et al.(2003)analyzed 311 wind profiles measured using a GPS dropsonde in the vicinity of hurricane eye walls between 1977 and 1999,and the drag coefficients were estimated from the wind profiles obtained from measurements made in several layers above the sea surface.The data shown in Fig.4b are the 10–100 m and 10–150 m layers estimates.As shown in Fig.4a,the experimental observations and theoretical values matched very well for lower wave ages when U10≤30 m s−1,meaning the model presented here more accurately predicts drag coefficients for young wave fields than was possible using the previous model(dotted line in Fig.4a),which does not take surface waves into consideration.However,as can be seen from Fig.4a,the drag coefficients measured in the laboratory did not decrease as the 10-m wind speed increased above 30 m s−1.This was not consistent with the theoretical results.In other words,breaking waves in young wave fields cannot generate enough ocean spray to decrease the drag coefficient.The theoretical solutions cover the range of existing field observations well,as shown in Fig.4b,and can be used to make predictions at high wind speeds when it may be difficult for certain field observations to be made.
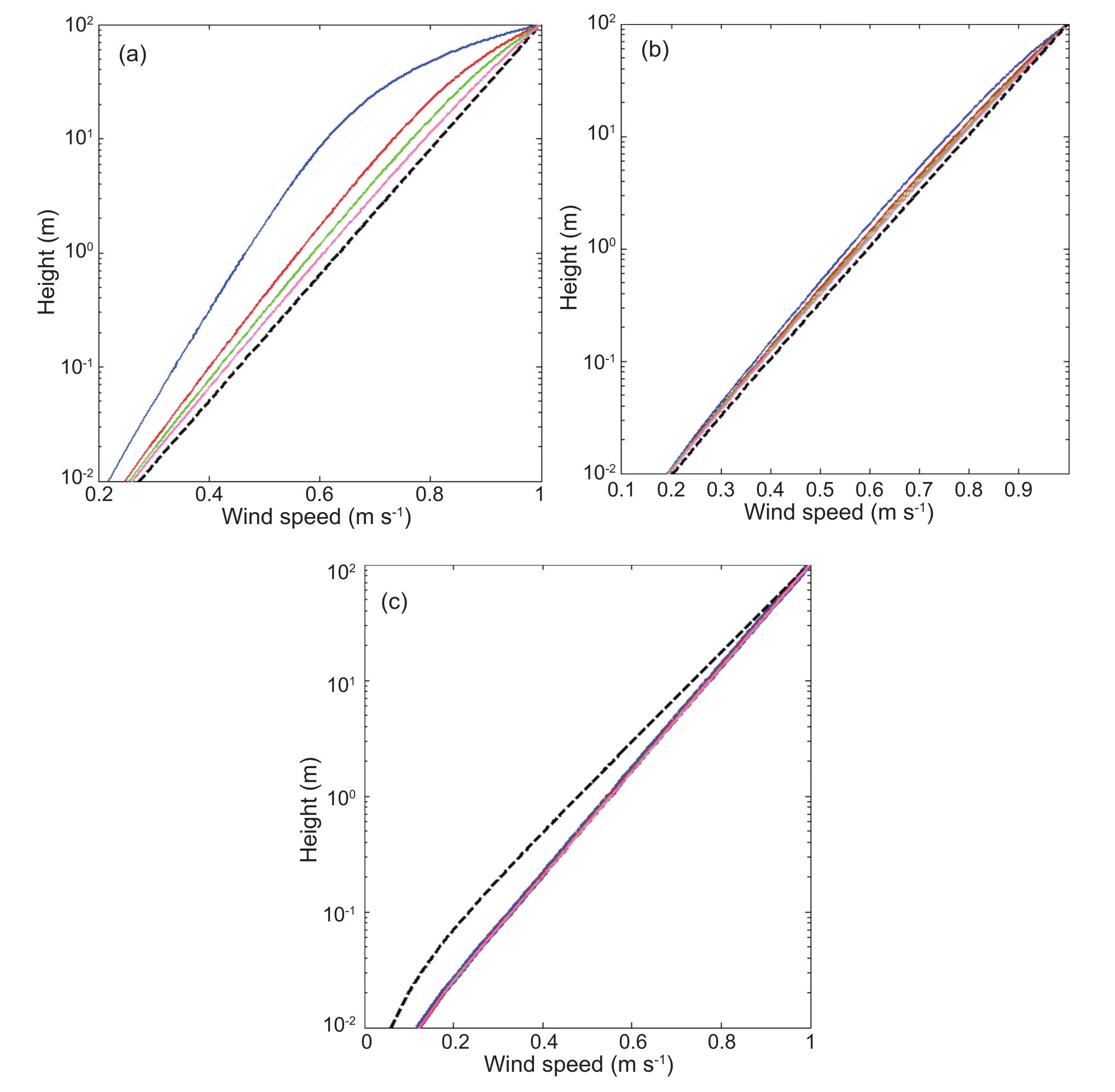
Fig.3.U(z)/Uhwind profiles for different wave ages for Uh=(a)15,(b)25 and(c)40 m s−1.The solid blue,red,green and pink lines show wind profiles for wave ages Ω∗=20,25,30 and 40,respectively.The dashed black lines show U0(z)/Uhwhen wave and spray effects are neglected.
5.Conclusion and discussion
The effects of surface waves and ocean spray on the MABL were studied by introducing wave-induced stress into the model of the MABL in the presence of sea-spray droplets described by Kudryavtsev and Makin(2011).A steady analytical solution to the wave-spray-modified model was obtained when the eddy viscosity coefficient was assumed to vary linearly with height.The main advantage of the model is that momentum exchange in the MABL can be investigated at low to extremely high wind speeds and different sea states,extending the research performed by Hara and Belcher(2004),who studied momentum exchange at low-to-moderate wind speeds,and by Kudryavtsev and Makin(2011),who investigated momentum distribution in the MABL under hurricane conditions.

Fig.4.Relationships between the drag coefficient Cd10and the 10-m wind speed U10.The solid lines show the results calculated using Eq.(28),taking into account the effects of surface waves and ocean spray(τw ≠ 0,τsp ≠ 0)for various wave ages Ω=0.2(blue),0.3(red),0.4(black),0.6(cyan),0.8(pink),and 1.2(green).The dotted lines show the results calculated taking only the effects of ocean spray(τw=0,τsp ≠ 0)into open green circles show data presented by Troitskaya et al.(2012).(b)The open black circles and asterisks show data presented by Powell et al.(2003)for the 10–100 m and 10–150 m layers,respectively.The vertical line around each data point shows the 90%confidence limit.
Illustrative examples for 100-m wind speeds of 15,25 and 40 m s−1,and surface wave fields with wave ages Ω∗=20,25,30 and 40,respectively,are presented.The growth rate β was determined using an expression proposed by Polnikov(2011),who investigated interactions between the air and surface waves.The directional JONSWAP spectrum described by Lucas and Soares(2015)and spray force defined by Kudryavtsev and Makin(2011)were both used to calculate the near-surface wind profiles over the ocean for different wind speeds and wave ages.The results were compared with the results obtained if wave-induced stress and/or spray stress was neglected.
The theoretical drag coefficients calculated using the model were compared with previous laboratory and field observations reported by Powell et al.(2003),Donelan et al.(2004),and Troitskaya et al.(2012).Comparing the laboratory observations with theoretical solutions showed that young sea-surface waves have considerable effects on the wind profile and turbulent structure in the MABL at lowto-moderate wind speeds.The drag coefficient and friction velocity were found to increase as the wind speed increased.However,at high wind speeds the drag coefficient started to level off and decrease as the wind speed increased,consistent with field observations.The results showed that ocean spray droplets produced by wind acting on breaking-wave crests affect the wind profile and turbulent structure,suppressing the sea-surface drag coefficient.In summary,including a wave induced component and spray component in the total stress allows the range of existing observations to be covered and the scatter in current observations to be predicted to some extent.
Although we have only presented results for the JONSWAP spectrum here,the model can also be applied to other wave spectra.The model has,of course,some weaknesses,including that the analytical drag coefficient values at high wind speeds for young wave fields were not consistent with laboratory data and the effects of mature sea waves on the wind profile and drag coefficient appeared to be too weak.We assumed that the Coriolis term can be neglected when calculating total stress,and that the eddy turbulent coefficient varies linearly with height.The parameterization of spray stress was found not to be related to the wave age.All the assumptions simplified the model construction and allowed the model to give relatively rational results.However,some common phenomena over the oceans,such as rain,atmospheric rolling,and large eddies,can markedly influence the MABL under certain conditions,but these physical processes were beyond the scope of this study.
Acknowledgements.The research presented in this paper was supported by the National Natural Science Foundation of China(Grant No.41576013)and the National Key Research and Development Program of China(Grant No.2016YFC1401404).The research also was supported by the National Natural Science Foundation of China(Grant No.41476021 and 41621064)and the Indo-Pacific Ocean Environment Variation and Air–Sea Interaction project(GASI-IPOVAI-04).
Andreas,E.L.,1998:A new sea spray generation function for wind speeds up to 32 m s−1.J.Phys.Oceanogr.,28,2175–2184, https://doi.org/10.1175/1520-0485(1998)028<2175:ANSSGF>2.0.CO;2.
Andreas,E.L.,2004:Spray stress revisited.J.Phys.Oceanogr.,34,1429–1440,https://doi.org/10.1175/1520-0485(2004)034<1429:SSR>2.0.CO;2.
Charnock,H.,1955:Wind stress on a water surface.Quart.J.Roy.Meteor.Soc.,81,639–640,https://doi.org/10.1002/qj.49708135027.
Donelan,M.A.,B.K.Haus,N.,Reul,W.J.Plant,M.Stiassnie,H.C.Graber,O.B.Brown,and E.S.Saltzman,2004:On the limiting aerodynamic roughness of the ocean in very strong winds.Geophys.Res.Lett.,31,L18306,https://doi.org/10.1029/2004GL019460.
Gao,Z.Q.,Q.Wang,and M.Y.Zhou,2009:Wave-dependence of friction velocity,roughness length and drag coefficient over coastal and open water surfaces by using three databases.Adv.At mos.Sci.,26,887–894,https://doi.org/10.1007/s00376-009-8130-7.
Grachev,A.A.,C.W.Fairall,J.E.Hare,J.B.Edson,and S.D.Miller,2003:Wind stress vector over ocean waves.J.Phys.Oceanogr.,33,2408–2429,https://doi.org/10.1175/1520-0485(2003)033<2408:WSVOOW>2.0.CO;2.
Hanley,K.E.,and S.E.Belcher,2008:Wave-driven wind jets in the marine atmospheric boundary layer.J.Atmos.Sci.,65,2646–2660,https://doi.org/10.1175/2007JAS2562.1.
Hara,T.,and S.E.Belcher,2004:Wind profile and drag coefficient over mature ocean surface wave spectra.J.Phys.Oceanogr.,34,2345–2358,https://doi.org/10.112275/JPO2633.1.
Harris,D.L.,1966:The wave-driven wind.J.Atmos.Sci.,23,688–693,https://doi.org/10.1175/1520-0469(1966)023<0688:TWDW>2.0.CO;2.
He,H.L.,and D.K.Chen,2011:Effects of surface wave breaking on the oceanic boundary layer.Geogphysical Research Letters,38,L07604.
Jarosz,E.,D.A.Mitchell,D.W.Wang,and W.J.Teague,2007:Bottom-up determination of air-sea momentum exchange under a major tropical cyclone.Science,315,1707–1709,https://doi.org/10.1126/science.1136466.
Kudryavtsev,V.N.,2006:On the effect of sea drops on the atmospheric boundary layer.J.Geophys.Res.,111,C07020,https://doi.org/10.1029/2005JC002970.
Kudryavtsev,V.N.,and V.K.Makin,2011:Impact of ocean spray on the dynamics of the marine atmospheric boundary layer.Bound.-Layer Meteor.,140,383–410,https://doi.org/10.1007/s10546-001-9624-2.
Lewis,D.M.,and S.E.Belcher,2004:Time-dependent,coupled,Ekman boundary layer solutions incorporating Stokes drift.Dyn.Atmos.Oceans,37,313–351,https://doi.org/10.1016/j.dynatmoce.2003.11.001.
Li,S.,M.Li,G.P.Gerbi,and J.B.Song,2013:Roles of breaking waves and Langmuir circulation in the surface boundary layer of a coastal ocean.J.Geophys.Res.Ocean,118,5173–5187.
Liu,B.,C.L.Guan,and L.Xie,2012:The wave state and sea spray related parameterization of wind stress applicable from low to extreme winds.J.Geophys.Res.,117,C00J22,https://doi.org/100.1007/s11802-016-2655-z10.1029/2011JC 007786.
Lucas,C.,and C.G.Soares,2015:On the modelling of swell spectra.Ocean Engineering,108,749–759,https://doi.org/10.1016/j.oceaneng.2015.08.017.
Makin,V.K.,2008:On the possible impact of a following-swell on the atmospheric boundary layer.Bound.-Layer Meteor.,129,469–478,https://doi.org/10.1007/s10546-008-9320-z.
Makin,V.K.,V.N.Kudryavtsev,and C.Mastenbroek,1995:Drag of the sea surface.Bound.-Layer Meteor.,73,159–182,https://doi.org/10.1007/BF00708935.
Mueller,J.A.,and F.Veron,2009:A sea state-dependent spume generation function.J.Phys.Oceanogr.,39,2363–2372,https://doi.org/10.1175/2009JPO4113.1.
Polnikov,V.G.,2011:Integrated model for a wave boundary layer.Marine Science,1,10–21,https://doi.org/10.5923/j.ms.20110101.02.
Powell,M.D.,P.J.Vickery,and T.A.Reinhold,2003:Reduced drag coefficient for high wind speeds in tropical cyclones.Nature,422,279–283,https://doi.org/10.1038/nature01481.
Rutgersson,A.,A.S.Smedman,and U.HÖgstrÖm,2001:Use of conventional stability parameters during swell.J.Geophys.Res.,106,27 117–27 134,https://doi.org/10.1029/2000 JC000543.
Semedo,A.,Ø.Saetra,A.Rutgersson,K.K.Kahma,and H.Pettersson,2009:Wave-induced wind in the marine boundary layer.J.Atmos.Sci.,66,2256–2271,https://doi.org/10.1175/2009JAS3018.1.
Song,J.B.,W.Fan,S.Li.,and M.Zhou,2015:Impact of surface waves on the steady near-surface wind profiles over the ocean.Bound.-Layer Meteor.,155,C00J21,https://doi.org/10.1007/s13131-016-0959-610.1007/s10546-014-9983-6.
Song,J.B.,2009:The effects of random surface waves on the steady Ekman current solutions.Deep-Sea Res.,56(5),659–671.
Troitskaya,Y.I.,D.A.Sergeev,A.A.Kandaurov,G.A.Baidakov,M.A.Vdovin,and V.I.Kazakov,2012:Laboratory and theoretical modeling of air-sea momentum transfer under severe wind conditions.J.Geophys.Res.,117,50–60,https://doi.org/10.1029/2011/JC007778.
Xiao,J.B.,and A.T.Taylor,2002:On equilibrium profiles of suspended particles.Bound.-Layer Meteor.,105,471–482,https://doi.org/10.1023/A:1020395323626.
Wang,J.J.,J.B.Song,Y.S.Huang,and C.H.Fan,2013:Application of the Hilbert–Huang transform to the estimation of air-sea turbulent fluxes.Bound.-Layer Meteor.,147(3),553–568,https://doi.org/10.1007/s10546-012-9784-8.
Zhang,T.,J.B.Song,S.Li,and L.G.Yang,2016:The effects of wind-driven waves and ocean spray on the drag coefficient and near-surface wind profiles over the ocean.Acta Oceanologica Sinica,35,79–85,https://doi.org/10.1007/s13131-016-0950-6.
Zhao,D.L.,and L.Xie,2010:A practical bi-parameter formula of gas transfer velocity depending on wave states.Journal of Oceanography,66,663–671,https://doi.org/10.1007/s10872-010-0054-4.
 Advances in Atmospheric Sciences2018年4期
Advances in Atmospheric Sciences2018年4期
- Advances in Atmospheric Sciences的其它文章
- Validation and Spatiotemporal Distribution of GEOS-5–Based Planetary Boundary Layer Height and Relative Humidity in China
- Evaluation of TIGGE Ensemble Forecasts of Precipitation in Distinct Climate Regions in Iran
- Evaluating the Capabilities of Soil Enthalpy,Soil Moisture and Soil Temperature in Predicting Seasonal Precipitation
- Large-scale Circulation Control of the Occurrence of Low-level Turbulence at Hong Kong International Airport
- Variations in High-frequency Oscillations of Tropical Cyclones over the Western North Pacific
- Idealized Experiments for Optimizing Model Parameters Using a 4D-Variational Method in an Intermediate Coupled Model of ENSO
