完全ASTFA方法及其在转子碰摩故障诊断中的应用

程军圣, 刘贞涛, 杨 宇

(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)

当转子系统出现故障时,其振动信号表现为非稳性，因此转子系统故障诊断诊断的关键是如何从非平稳信号中提取故障信息[1]。

经验模态分解(Empirical Mode Decomposition, EMD)是一种完全由数据驱动的信号分解方法，非常适合非线性、非平稳信号处理[2]。然而，EMD本身也存在一些问题，其中模态混淆就是一个突出的问题，严重的模态混淆会使得分解出的内禀模态分量(Intrinsic Mode Function,IMF)波形失真，失去物理意义。针对EMD存在的模态混淆问题，WU等[3]提出了集合总体平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)。EEMD通过向信号中添加白噪声来辅助分解，通过平均来削减分量中的噪声残余，能够有效地抑制EMD的模态混淆，但是EEMD的分解效果依赖于加入噪声的幅值大小和总体平均次数。

自适应最稀疏时频分析(Adaptive and Sparsest Time-Frequency Analysis，ASTFA)是Hou等[4]近年提出的一种新的时频分析方法。该方法把信号分解问题转化为一个非线性优化问题，具有坚实的数学基础。与EMD方法相比，ASTFA方法在抑制端点效应、模态混淆方面具有一定的优势，已经被成功应用于瞬时频率估计、机械故障诊断、结构损伤检测、信号降噪等领域[5-7]。然而，在用ASTFA方法对信号进行分解时必须确定一个影响分量频带带宽的参数λmax，当这个参数选用不理想，会产生模态混淆[8]。由于带宽控制参数需要人为设定，从这个意义上讲ASTFA的自适应性并不彻底。

虽然ASTFA方法在一些领域得到了运用，但是学者们主要是把ASTFA当作前处理工具，并未对如何合理地确定λmax进行深入研究。为了避免将λmax设定为定值导致ASTFA方法产生模态混淆，提高ASTFA方法的自适应性，本文提出完全自适应最稀疏分解(Complete Adaptive And Sparsest Time-Frequency Analysis,CASTFA)。该方法以EEMD分解出的分量为参考信号，提高了分解的自适应性，抑制了ASTFA方法的模态混淆。

1 完全ASTFA

1.1 ASTFA方法

ASTFA认为单分量应该满足以下两个条件：

(1)瞬时频率大于0；

(2)幅值函数比纯调频函数光滑；

ASTFA分解出一个分量主要有以下步骤：

(1) 构建一个过完备字典库：

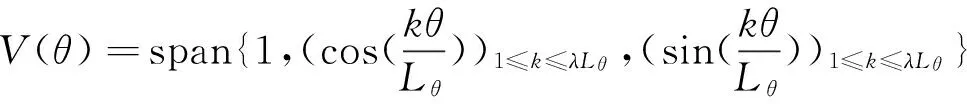
0<λ≤λmax<1

(1)

(2) 从过完备字典中选择一个最优原子，即解决以下优化问题：

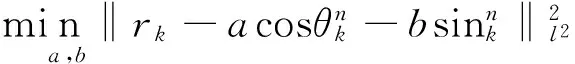
(2)

在步骤(1)λ≤λmax中是是为了满足条件(2)，而θ′(t)≥0则保证条件(1)。

每分解一个分量，都预先要确定一个λmax，给出一个相位函数初值θ0， Hou等给出λmax=1/2，以FFT估计相位函数初值θ0，并且指出以FFT估计相位函数初值能得到很好的效果，λmax的取值对ASTFA的分解有着重要影响，若λmax过小可能使得一个尺度被分解成多个分量，若λmax过大则可能使得一个分量包含多个尺度，即λmax控制着分解出的分量的频带带宽。

1.2 CASTFA方法

由于ASTFA分解中参数λ的最大值λmax对于分解出的分量具有重要影响：λmax的选择不当会引起模态混淆。为了保证分解的自适应性，λmax应该随信号的不同而改变，然而Hou等在提出ASTFA时，将λmax取为1/2，这使得ASTFA方法的自适应性不彻底，当λmax与理想值相差较远时，ASTFA方法的分解效果不佳。

EEMD以EMD方法为核心，具有很好的自适应性，且有效地抑制EMD的模态混淆现象。先对信号进行EEMD，依次以分出的IMF估计ASTFA分解所需要的相位函数，以保证EEMD方法与CASTFA方法得到的分量是同一尺度下的，再以不同的λmax进行ASTFA分解，得到一系列分量，从中选出与相应的IMF相关程度最高的分量为理想分量，其对应的λmax则为理想的λmax。上述方法能够借助EEMD的自适应性，根据信号自身特点自动地确定λmax，分解不同的信号甚至是同一信号的不同分量所采用的λmax都可能不同，使ASTFA的自适应性更为彻底,称为完全自适应最稀疏分析(Complete Adaptive and Sparsest Time-Frequency Analysis，CASTFA)，将CASTFA分解出的分量称为完全自适应分量(Complete Adaptive Function，CAF)，将ASTFA分解出的分量称为自适应分量(Adaptive Function，AF)。

EEMD是对信号加入噪声再进行EMD分解，通过多次平均来消除噪声在分量中的残余。虽然增加平均次数可以减少分量中的噪声残余，但是这一方面会影响EEMD的效率，另一方面噪声始终无法完全消除。EEMD的分解效果还受加入噪声幅值的大小影响，幅值过大会破坏低频成分的极值分布，容易产生低频模态混淆，幅值过小，对高频成分的“拉动能力”较弱，容易产生高频模态混淆[9]。ASTFA分解过程不用加入噪声，因此分量中不会存在噪声残余。ASTFA的模态混淆是由于λmax的选用不当引起，若选择的λmax很理想，就可以认为ASTFA分解出的分量是理想分量。

EEMD方法和CASTFA方法中对单分量的具体定义不一样的，但都是对同一对象的叙述，只是角度不同。在理想情况下，用两种方法分解同一信号，在同一尺度下的分量应该具有很高的相关性。即使EEMD方法由于参数选定不理想，导致其分量出现一定的波形失真，其分解出的分量也会包含一定的尺度信息，与CASTFA分解出的理想分量也有相对较好的相关性。所以，可以以同一尺度下的两种方法得到的分量之间的相关性作为评价指标来确定最优的λmax，这就是CASTFA的理论基础。

根据Wu等推荐，本文涉及的EEMD参数确定为：加入噪声幅值e=0.2，总体平均次数M=100，考虑到转子故障信号往往呈现窄带特性，把λmax的取值区间定为(0,1/2),以提高效率。CASTFA的具体流程见图1。

图1 CASTFA流程图Fig.1 The flow diagram of CASTFA

图1中：m为CASTFA分解分量个数控制变量，每分解出一个分量，其值增加1；res为信号分解余量；θ0为相位函数初值；t为时间序列；k为λmax寻优的迭代代数控制参数；AF为ASTFA分解出的分量；AFs为AF分量集合；AFs[k]为AFs中第k个AF分量；CAFm为CASTFA分解出的第m个分量。

2 仿真分析

构造如下仿真信号：

式中：x1、x2均为调幅调频信号；x3为一余弦信号；xn为噪声信号，各个信号的波形如图2所示。

图2 仿真信号的三个分量及仿真信号Fig.2 The time domain waveforms of three components of the simulation signal and itself

分别用ASTFA、EEMD、CASTFA方法对上述信号进行分解，分解个数定为5个。分解结果如图3～图5所示。从分解结果来看，ASTFA方法能够较好地分解出x3，而分解出x1、x2时，产生了明显的模态混淆;EEMD方法在分解高频分量时，能够较好地抑制模态混淆，但是在分解低频分量时产生了严重的模态混淆，从上面的讨论可知，这是由于EEMD参数的选择不合理导致的。CASTFA方法能够较好地分解出3个分量，很好地抑制了模态混淆，效果优于ASTFA和EEMD方法。从这个结果可以看出CASTFA方法对EEMD的中的参数选定不敏感，即使EEMD分解效果不理想，对应的CASTFA分解效果依然可以较好。

图3 ASTFA分解结果Fig.3 The ASTFA decomposition results of the simulation signal

图4 EEMD分解结果Fig.4 The EEMD decomposition results of the simulation signal

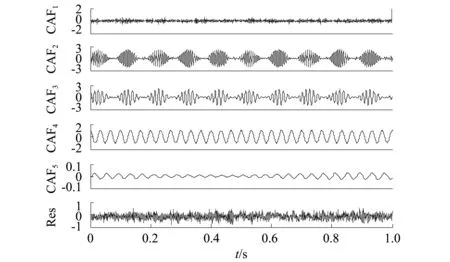
图5 CASTFA分解结果Fig.5 TheCASTFA decomposition results of the simulation signal

3 应用实例

仿真结果表明，与EEMD、ASTFA相比，CASTFA具有更好地抑制模态混叠现象，将本方法应用于实际的转子单点局部碰摩故障诊断。采用一段实测转子系统的振动位移信号，额定转速为3 000 r/min,则额定转频为fr=50 Hz,记X=fr，采样频率为4 096 Hz。该信号(去除了直流)的时域图与幅值谱如图6，7所示。

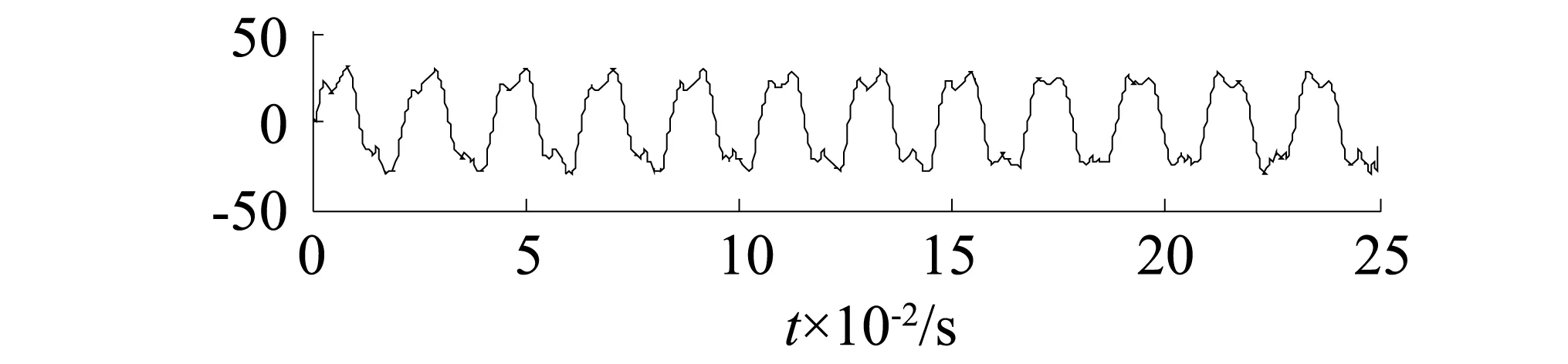
图6 时域波形Fig.6 The time domain waveforms and frequency spectrum

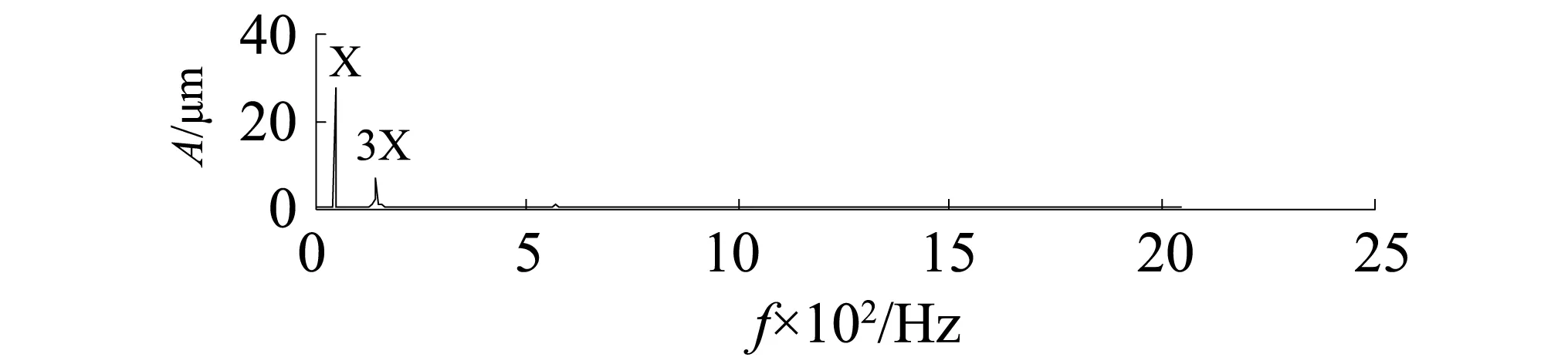
图7 幅值谱Fig.7 Amplitude spectrum

在转子位移信号的幅值谱中，转频及其3倍频较为突出，而包含碰摩故障信息的其他分量无法明显识别出。为此，CASTFA方法对信号进行分解，分解个数定为6个,结果如图8。作为对比也用ASTFA方法分解，结果如图9。

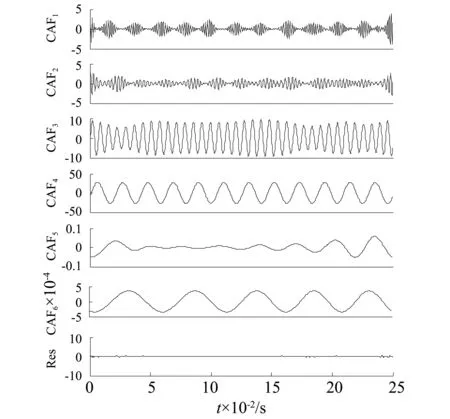
图8 CASTFA分解结果Fig.8 CASTFA decomposition results

从CASTFA分解结果来看，CAF1、CAF2具有明显的调幅特性，CAF3、CAF4表现出很强的周期性，CAF5、CAF6幅值非常小，是背景噪声。

从ASTFA分解结果来看，AF1、 AF2的分解效果较好，分别与CASTFA分解出的CAF4、CAF3相对应，都表现出很强的周期性。然而AF3、 AF4、AF5三个分量有明显的模态混叠现象。与CAF1对应的分量成分分散在了AF3、 AF5两个分量中，而与CAF2对应的分量成分也分散在了AF3、 AF4两个分量中。显然，在抑制模态混淆方面，CASTFA方法表现比ASTFA方法更加优越。

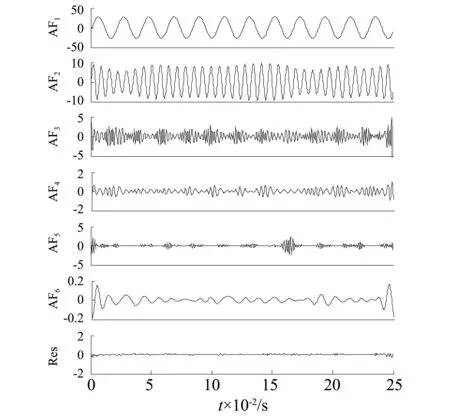
图9 ASTFA分解结果Fig.9 ASTFA decomposition results

为了更好地对振动信号进行分析，对CAF1、CAF2做包络谱，对CAF3、CAF4做频谱，结果如图10～11所示。

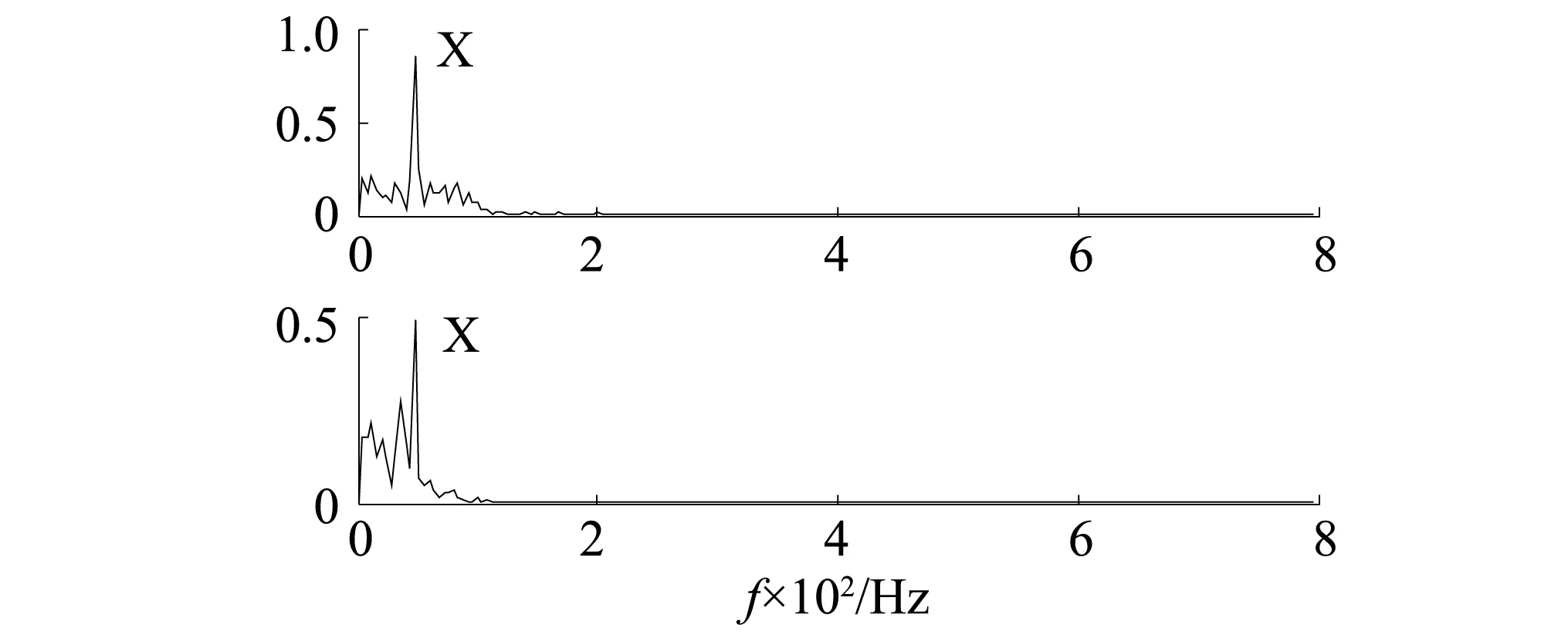
图10 CAF1、CAF2包络谱Fig.10 The envelope spectrum of CAF1、CAF2

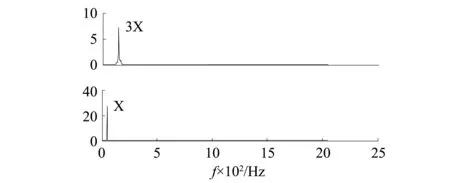
图11 CAF3、CAF4幅值谱Fig.11 The frequency spectrum of CAF3 and CAF4

从频谱分析来看CAF3、CAF4分别为3X、X分量，与原始信号的频谱相对应，从包络谱来看，X频率处幅值明显很大，即其调幅的频率刚好是转频[10]。对转子在不同状态下的波形特征进行了研究，结果表明只有当转子发生碰摩故障时，其振动信号分量才会表现出很强的调幅特性。调幅频率正好是转频，这是因为转子每转一周，动、静件就摩擦一次，因此CAF1、CAF2包含了重要的碰摩信息。因此，CASTFA方法能够有效地提取转子局部碰摩信息，可以用于转子局部碰摩的故障诊断。

4 结 论

(1)针对ASTFA方法由于参数λmax选用不当而导致模态混淆的问题，提出了CASTFA方法。CASTFA方法利用EEMD方法的自适应性，解决了参数λmax的选定问题，避免了人为选定参数λmax的缺陷。

(2)仿真分析表明CASTFA在抑制模态混淆现象方面要优于ASTFA、EEMD方法。

(3)将CASTFA应用到转子系统单点局部碰摩的故障诊断中，不仅得到了转频及其倍频成分，也得到了表征碰摩故障的以转频为调制频率的高频调幅成分，成功地提取了故障信息。

[ 1 ] 于德介，陈淼峰，程军圣，等.基于EMD的奇异值熵在转子故障诊断中的应用[J].振动与冲击，2006，25(2): 24-27.

YU Dejie，CHEN Miaofeng，CHENG Junsheng，et al. Fault diagnosis approach for rotor system Based on EMD method and singular value entropy[J].Journal of Vibration and Shock, 2006,25(2): 24-27.

[ 2 ] HUANG N E，SHEN Z，LONG S R，et al. The empirical mode decomposition and the Hilbert spectrumfor nonlinear and non-stationary time series analysis[J].Proceeding of the Royal Society ： A Mathematical Physical & Engineering Sciences，1998，454： 903-995.

[ 3 ] WU Z H，HUANG N E. Ensemble empirical modedecomposition：A noise assisted data analysis method[J].Advances in Adaptive Data Analysis，2009(1)： 1-41.

[ 4 ] HOU T Y，SHI Z Q. Adaptive data analysis via sparse time-frequency representation[J].Advances in Adaptive Data Analysis，2011，3(1/2): 1-28.

[ 5 ] 杨宇，李紫珠，何知义，等.基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断[J].中国机械工程，2015，26(21): 2934-2940.

YANG Yu，LI Zizhu，HE Zhiyi，et al. The rolling bearing fault diagnosis method based on ASTFA De-nosing and AKVPMCD[J]. China Mechanical Engineering，2015，26(21): 2934-2940.

[ 6 ] 李宝庆，程军圣，彭延峰，等.基于ASTFA的广义解调方法及其应用[J].中国机械工程，2015，26(19): 2565-2570.

LI Baoqing，CHENG Junsheng，PENG Yanfeng，et al. Generalized demodulation method based on ASTFA method and its applications[J].China Mechanical Engineering，2015,26(19): 2565-2570.

[ 7 ] 杨斌，程军圣.基于自适应最稀疏时频分析的结构损伤检测方法[J].振动工程学报，2015，28(4): 640-649.

YANG Bin，CHENG Junsheng. The damage detection method base on the adaptive and sparsest time-frequency analysis[J]. Journal of Vibration Engineering，2015,28(4): 640-649.

[ 8 ] HOU T Y，SHI Z Q. Data-driven time-frequency analysis[J].Applied and Computational Harmonic Analysis，2013，35(2): 284-308.

[ 9 ] 雷亚国，孔德同，李乃鹏，等.自适应总体平均经验模态分解分解及其在行星齿轮箱故障检测中的应用[J].机械工程学报，2014，50(3)：64-70.

LEI Yaguo，KONG Detong，LI Naipeng，et al.Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of Mechanical Engineering，2014，50(3)： 64-70.

[10] 程军圣,于德介，杨宇，等.EMD方法在转子局部碰摩故障诊断中的应用[J].振动、测试与诊断，2006，26(1): 24-27.

CHENG Junsheng，YU Dejie，YANG Yu, et al. Application of EMD to local rub-impact fault diagnosis in rotor systems[J]. Journal of Vibration，Measurement &Diagnosis，2006，26(1): 24-27.