基于PBM和DPM的喷雾冷冻流化床液滴雾化的数值模拟

李苗苗，徐 俊，王 新，徐 庆

（天津科技大学 机械工程学院；天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津300222）

液滴在固体表面的流动变化，历来是工程领域的一个研究热点，张建林等[1]就对液滴在固体表面的铺展情况进行了研究。流化床包覆是指芯材在某一温度流化气体的流化作用下处于流化状态，雾化的壁材与芯材接触将芯材包埋的技术，也是微胶囊常用的制备技术[2]。包覆的壁材既可以是亲水性的糖类或蛋白类，又可以是亲脂性材料。Litster等[3]认为包覆的过程主要分为3个步骤：1）液滴的润湿和成核；2）颗粒的固化和生长；3）颗粒间磨损破碎，该理论也被用来解释流化床包覆过程。Link等[4]总结了影响包覆效果和包覆过程的影响因素，主要分为液体特性、固体特性、系统和操作变量。

在顶喷的流化床包覆过程中，主要包括气体的流化作用、液滴的雾化作用、颗粒与液滴之间的碰撞以及液滴在颗粒表面的沉积铺展等等。雾化液滴在流化床内随机运动进行碰撞，碰撞过程中，如果2个表面润湿的颗粒接触，会形成液桥，颗粒在冷空气的作用下，固化会导致液桥向固桥转变，形成团聚。颗粒的团聚和破碎经历很多微观过程，需要引进群体平衡模型（population balance model，PBM）[5]计算颗粒的一些变量，如粒径分布、润湿颗粒的数量等。

PBM的模拟对象主要是多相流中副相的粒径分布情况，如液滴、气泡以及固态颗粒等，需要得到合适的粒径分布规律[6-9]。计算粒径分布主要有2种方法，一种是拉格朗日法，即离散相模型（discrete phase model，DPM），另一种是欧拉法，即PBM法。由于DPM主要模拟离散相，且仅限于稀疏相的模拟，群体平衡模型因为稀疏相均可以模拟而被广泛提出。

本文中基于PBM和DPM，对喷雾冷冻流化床包覆过程中的雾化液滴的产生、凝固、运动进行了数值模拟，主要对雾化过程中的速度、温度及颗粒的团聚破碎规律进行了研究。

1 数学模型

在过去的几十年时间里，计算流体动力学（computational fluid dynamics，CFD）已被广泛应用于喷雾领域，比如雾滴的沉积特性研究[10]、雾化效果的研究[11]等，各种数值方法，例如流体体积法、DPM已经用于预测喷嘴的雾化特性和预测液滴的轨迹[12]。DPM方法是基于拉格朗日计算方法[13]，液滴轨迹使用单独的控制方程计算；而体积流体应用欧拉法，把各相看作是相互联系的相计算。模拟粒子过程主要有PBM和DPM两大体系[14]。

1.1 气相控制方程

计算流体力学需要了解流体的动力特性，这对研究雾化过程中的流场分布有着很重要的意义，因此，为了得出流体的流速与压力等动力学特性，在计算中，将空气作为连续相介质处理，采用SIMPLE算法求解，方程的通用形式表示为

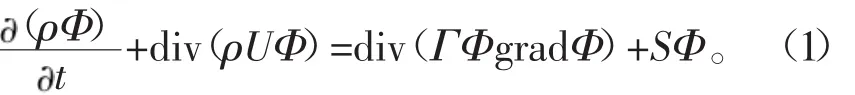
式中：Φ为通用变量；ΓΦ为广义扩散系数；SΦ为广义源相。

1.2 群体平衡模型

雾化液滴在运行的过程中会出现，聚并和破碎的行为，这在研究流化床包覆的过程中也是必须要考虑的，关于颗粒的聚并和破碎的研究，在实验中难以控制和实现，因此本研究中引入了群体平衡模型。群体平衡模型是一组描述颗粒聚并和破碎行为的偏微分方程[15-16]，反映颗粒成长和消亡的过程。其一般表示形式为

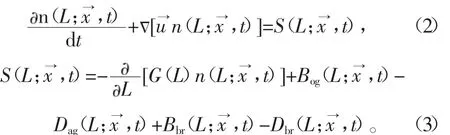
1.3 离散相模型

利用DPM可以对颗粒进行追踪，因为它是在欧拉-拉格朗日法的基础上建立的，所以认为液滴或颗粒是控制体内动量、质量和能量的源项。

由流化床顶部雾化器生成液滴的直径是一组离散的尺寸，并且每种尺寸的液滴都各有其运动轨迹，沿着该轨迹的液滴的流动速度是固定的。在设定了空气的温度和速度后，各组尺寸液滴的控制方程就会进行迭代，计算它们的速度、轨迹、尺寸和温度，直到这些液滴到达喷雾流化床的出口或碰撞到壁面。

追踪颗粒轨迹是通过计算力平衡方程实现的，力平衡方程为：

式中：v为连续相速度；up为颗粒速度；ρga为连续相密度；ρp为颗粒密度。

作用在颗粒上的力有重力、惯性力以及气体曳力。

滑移雷诺数（Re）和曳力系数（CD）的计算公式为

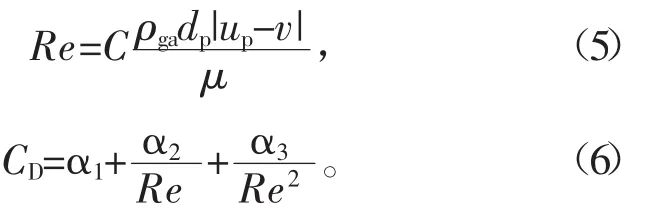
式中：dp为颗粒直径；α1、α2、α3为颗粒球形度系数。

2 模型的建立

本几何模型对喷雾流化床的模型[17]进行简化，计算域如图1所示。

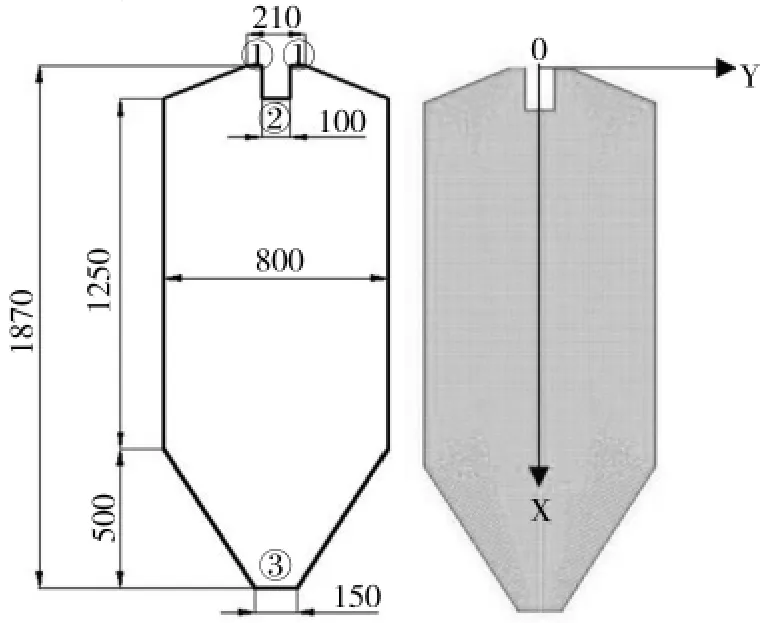
图1 几何模型尺寸和网格Fig.1 Size of geometric model and mesh

本研究中模型为柱锥形流化床，计算域使用二维空间进行模拟，几何体相关尺寸参数及模型参数见表1。表中所列数据是参考了耿县如等[17]的单液滴喷雾冷冻研究的有关数据，并进行了相关修改。

3 计算结果及讨论

3.1 液滴的温度

图2为液滴温度随时间的变化图。

表1 边界条件和参数Tab.1 Boundary conditions and simulation parameters

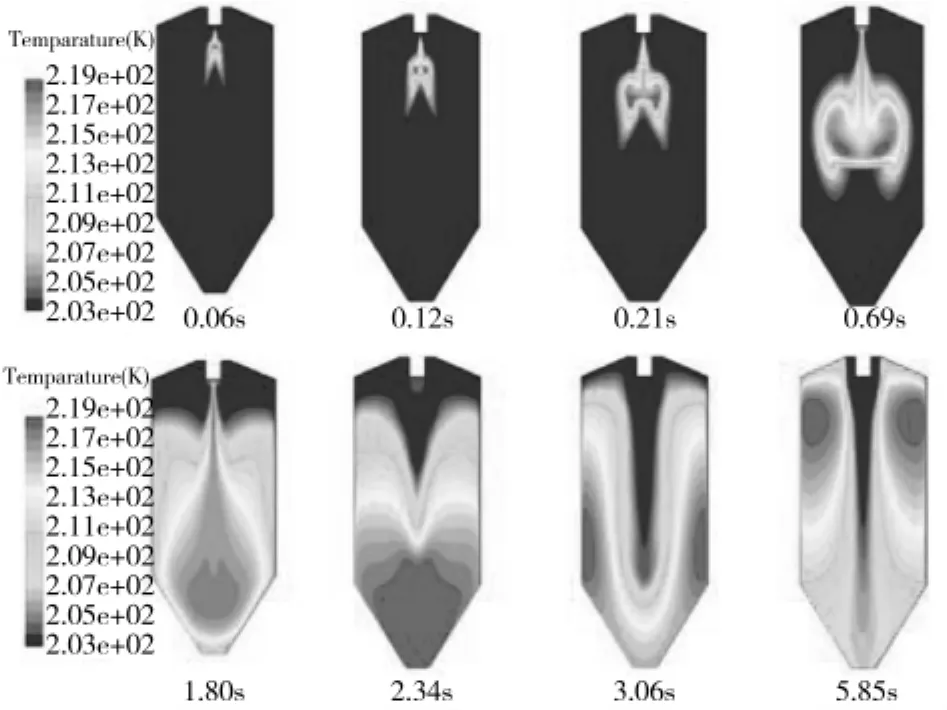
图2 液滴温度随时间的变化Fig.2 Change of droplet temperature with time

由图可知，液滴从入口喷出，在喷出时液滴温度为300 K，由于环境温度很低，为203 K，因此液滴在达到底部时已成凝固状态。整个过程中，流化床内温度在X轴两侧呈对称分布，经过1.8 s到达锥体体部分，随即底部温度达到最大，继而产生回流，之后流化床内温度又呈对称分布。整个过程当中，只有1.8 s到2.34 s底部温度达到最大，到达5.85 s以后流化床内温度在X轴两侧又呈对称分布，这是因为雾化液滴在运动过程中，中心区域流速较大，所以会很快达到底部，而当整个过程达到稳定的过程中，雾化液滴与冷空气接触，温度也逐渐下降，同时达到底部又产生回流，最终又呈现出两边的对称分布。

本研究中以模型液滴入口为坐标原点，轴向为X方向，指向底部椎体部分的方向为X轴正方向。结果显示，以X轴为轴线，两边成对称分布，因此以下图像只采取了模型的一半进行了研究。

图3为流化床内温度随Y轴的变化图。如前所述，雾化液滴的温度会对液滴的雾化产生影响，因为液滴在温度过低时会产生凝固现象。在流化床包覆过程中，一旦液滴涂敷在颗粒表面，是需要进行冷却的，因此本文也研究了流化床内的温度分布。

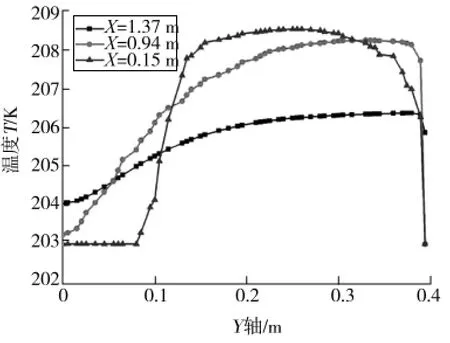
图3 流化床内温度随Y轴的变化Fig.3 Temperature change with axis Y in a fluidized bed

图3说明了雾化液滴在不同轴向位置上的温度从Y=0 m处到壁面处的温度变化，冷气入口接近液滴喷射入口。由于冷气初始温度和几何模型壁面温度都均为203 K，而液滴温度为常温300 K，因此液滴在与冷气接触后，温度会很快下降。因为流化床中心部位是气体的喷射区，所以中间部位的温度很低，由中心向两边温度逐渐升高，而在壁面处，由于液滴的回流，会使得液滴能量损失，温度与壁面温度接近，因此出现流化床内接近壁面处温度陡降，这与耿县如等[17]所做关于液滴喷雾冷冻的温度变化和分布规律相类似。

3.2 雾化液滴的运动

图4为液滴在气液两相流的雾化特性图。由图4a可以看出，液滴从入口进入流化床内，液滴均具有一定初速度，因此液滴会很快到达流化床底部壁面，碰到壁面后，由于冲量作用，其方向发生了改变，这就会使得碰到流化床底部的液滴产生向上的回流，如图4b所示。同时使得液滴的速度呈现出沿轴向逐渐减小，沿径向中心高两边低的现象，如图4c所示。这说明在液滴雾化的过程中，由于几何模型结构的作用，会产生一定的回流这将对液滴雾化产生影响。同时比较图4c和图4d也可以看出，PBM模型和DPM模型在计算液滴雾化过程中有着相同的速度场分布，这与Taghipour等[13]对气固流化床的研究结论是一致的。同时PBM又可以用于液滴的粒径分布研究，因此本文采用了PBM模型来研究液滴的粒径变化和分布情况。

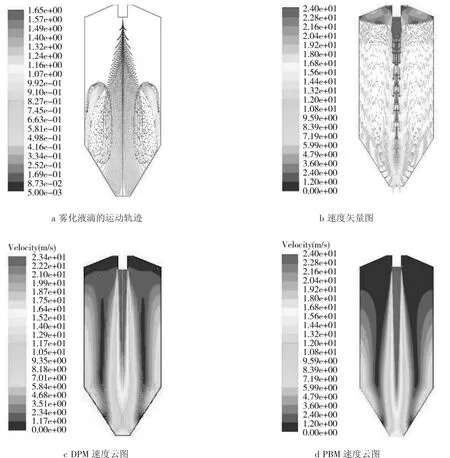
图4液滴在气液两相流的雾化特性Fig.4 Atomization characteristics of droplets in gas-liquid two-phase flow

3.3 液滴的速度

图5为液滴X方向速度随Y坐标的变化图。

雾化液滴之间会出现团聚和破碎的现象，这直接关乎液滴的雾化效果，同时也会对流化床包覆的研究产生影响。速度和温度的分布对雾化液滴的团聚和破碎有着很大影响。

图5a、5b说明了PBM和DPM模型在对液滴雾化进行计算过程中，在轴向上不同位置液滴轴向速度从Y=0处向壁面接近的变化。液滴的初速度为25 m/s，液滴喷出后，在几何模型的中部，液滴有能量损失，因此图中液滴在X=0 m处速度为23 m/s，并且越接近几何体壁面，液滴的速度越小。在Y=0.21 m处液滴速度为零，从Y=0.21 m处到壁面即Y=0.4 m处，液滴速度方向改为向上，这是因为液滴在碰到壁面以后出现了回流现象，回流又会导致液滴之间的接触和碰撞。这一现象将会使液滴的粒径发生变化，同时由图可知，2种模型的计算结果吻合，这也说明了由图4c、d得出的可以用PBM来研究液滴的粒径变化和分布情况的结论。

3.4 液滴的粒径分布

本文中粒径分布是指液滴在某种粒径下的液滴数量，其具体分布情况如图6所示。

图6a、b、c表明了雾化液滴轴向上不同位置的粒径分布，液滴的初始粒径为1.26 μm。由图可知，液滴在雾化过程中发生了团聚和破碎现象，形成了粒度不一的分布。团聚体数量最大的粒径范围为2.4～3 μm，最小范围为0～0.5 μm。在轴向上，离喷口越远处，液滴的团聚现象越明显，即2.4～3 μm的液滴数量越多，而0～0.5 μm、0.5～0.79 μm的液滴数量比较少。这是因为在流化床的中心部位气体的温度，速度较大，而随着液滴向流化床边缘不断的运动，液滴出现了团聚和破碎的现象如图6d所示，ddroplet表示液滴的粒径。由液滴的累积粒度曲线可以看出，液滴在喷口处和末端部位的数量是最多的，这主要是因为在流化床顶部接近入口处液滴速度较大，而在接近底部椎体部分液滴的碰撞比较明显，碰撞后形成的小颗粒数量较多。

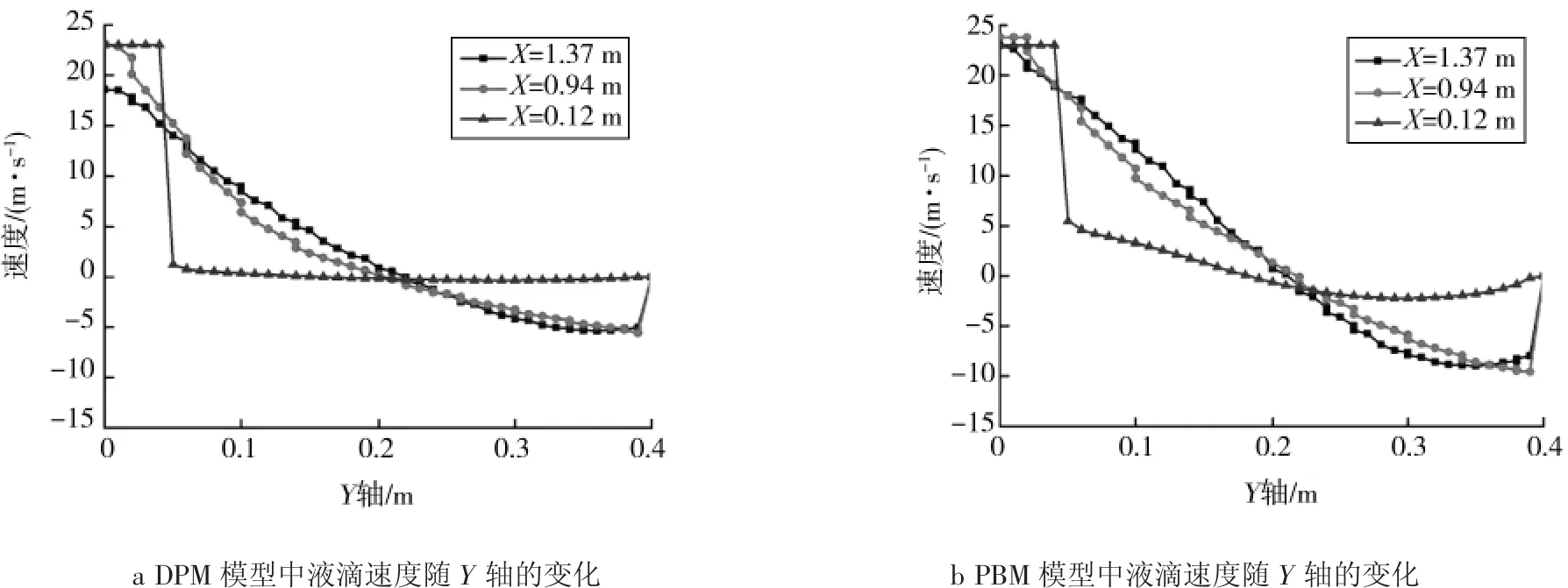
图5 液滴X方向速度随Y坐标的变化Fig.5 Change of X direction velocity of droplet with Y coordinate

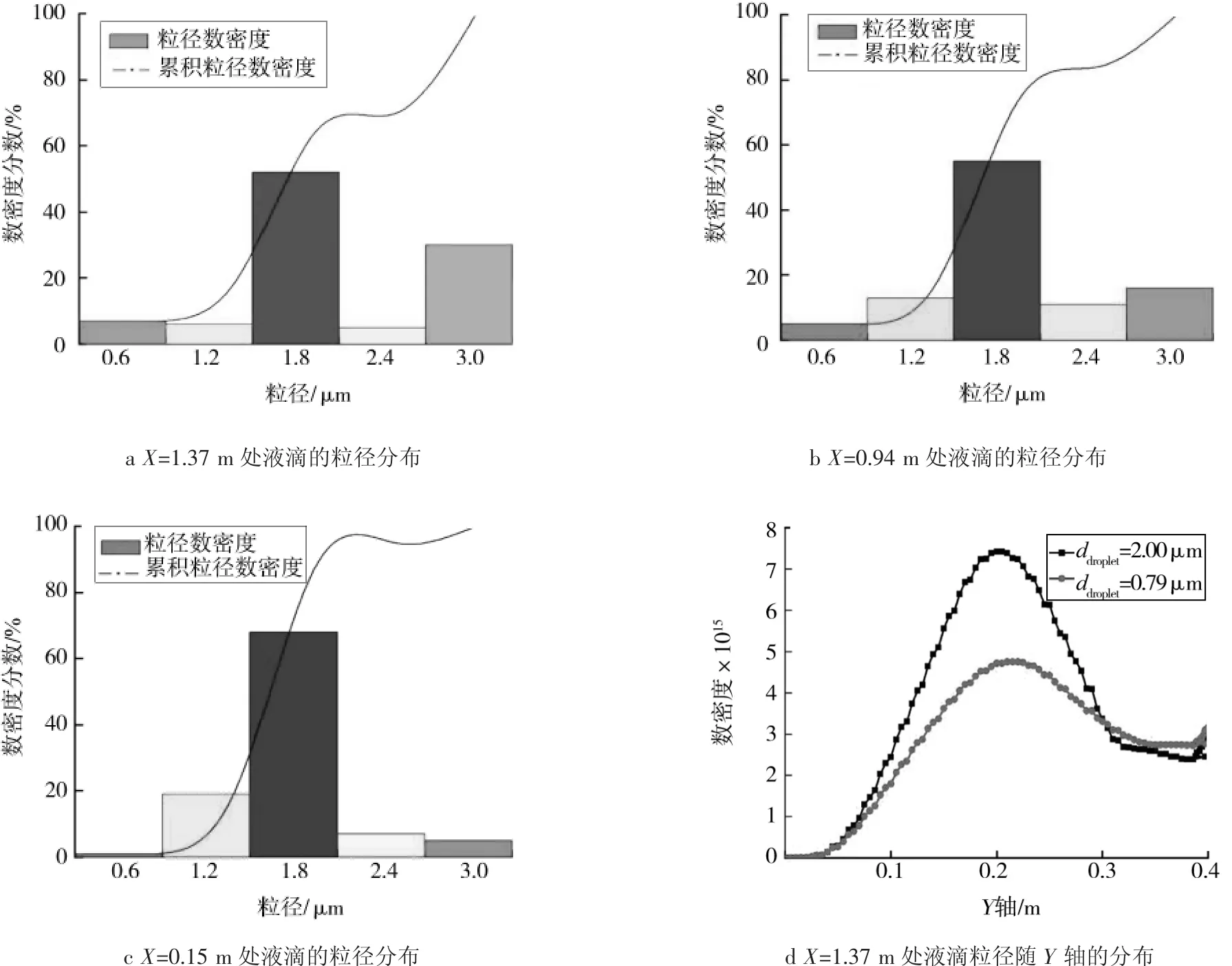
图6雾化液滴的粒径分布Fig.6 Particle size distribution of atomized droplets

图6b表示的是X=1.37 m直线上的液滴在径向由中心向两边运动的过程中，1.8～2.4、0.6～1.2 μm粒径的液滴数量的变化。由图可知，由于初始粒径为1.26 μm，在Y=0～0.2 m的过程中，液滴同时存在团聚和破碎现象，因此才会出现了1.8～2.4、0.6～1.2 μm的液滴数量不断增加的现象。在Y=0.2 m处以后流化床内的温度开始越来越接近壁面温度即T=203 K，因此颗粒的温度开始逐渐降低出现凝固现象，团聚后难以破碎，2.5～3 μm的液滴数量分布比较多，所以1.8～2.4、0.6～1.2 μm的液滴，尤其是1.8～2.4 μm的数量在这一区域比较少（说明：雾化的液滴在实际过程中由于喷嘴的作用，液滴可以被分散成很细小的单个液滴，出现几微米的液滴属合理现象）。

综上所述，由模拟结果可知，液滴在雾化过程中，由于流化床壁面和入口气体的温度都为203 K，与液滴初始温度相差较大，因此接近壁面处流化床内温度会出现陡降。同时由于液滴的初速度为28 m/s，因此液滴在短时间内到达底部椎体部分，产生回流，造成液滴自身的能量损失，而这将会使接近壁面处的液滴出现大量团聚。

4 结论

本文中基于CFD中的群体平衡模型对流化床内液滴的雾化行为进行了二维数值模拟，并与离散相模型的计算结果进行对比，结果表明，群体平衡模型和离散相模型可以得出相同的速度场分布，群体平衡模型可以进一步得出更为详细的粒径分布，故群体平衡模型可以作为离散相模型的替代模型进一步研究液滴的聚并和破碎行为。

流化床内温度呈现中间低、两边高的状况，在液滴碰到锥形壁面时液滴产生回流，液滴在这一区域很容易团聚。在中心区域液滴速度较大，破碎现象比较明显。

（

）：

[1]张建林，刘邱祖，赖成，等.液滴在固体表面流动特性的数值模拟及验证[J].中国粉体技术，2016（3）:19-21.

[2]NIENOWA W.Fluidised bed granulation and coating:applications to materials，agriculture and biotechnology[J].Chemical Engineering Communication，1995，139：233-253.

[3]LITSTER J，ENNIS B.The science and engineering of granulation processes[J].Particle Technology，2004，15.

[4]LINK K C，ERNST-ULRICH S.Fluidized bed spray granulation investigation of the coating process on a single sphere[J].Chemical Engineering and Processing 1997，36：443-457.

[5]MUBASHIR，HUSSAIN，JITENDRA，et al.A new framework for population balance modeling of spray fluidized bed agglomeration[J].Particuology，2015，19（2）:141-154.

[6]REYNOLDS G K.Modelling of pharmaceutical granule size reduction in a conical screen mill[J].Chemical Engineering Journal，2010，164（2/3）:383-392.

[7]GRIFFIN D W，MELLICHAMP D A，DOHERTY M F.Reducing the mean size of API crystals by continuous manufacturing with product classification and recycle[J].Chemical Engineering Science，2010，65（21）:5770-5780.

[8]MORTIER S T F C，GERNAEY K V，BEER T D，et al.Development of a population balance model of a pharmaceutical drying process and testing of solution methods[J].Computers&Chemical Engineering，2013，50（9）:39-53.

[9]BASHEER I A，HAJMEER M.Artificial neural networks:fundamentals，computing，design，and application[J].Journal of Microbiological Methods，2000，43（1）:3.

[10]孙国祥，汪小旵，丁为民.基于CFD离散相模型雾滴沉积特性的模拟分析[J].农业工程学报，2012，28（6）:13-19.

[11]梁钦，高贵军，刘邱祖.压力型雾化喷嘴射流喷雾气-液两相流数值模拟[J].中国粉体技术，2015，21（2）:5-9.

[12]DUANGKHAMCHAN W，RONSSEWF，DEPYPERE F，et al.CFD study of droplet atomisation using a binary nozzle in fluidised bed coating[J].Chemical Engineering Science，2012，68（1）:555-566.

[13]TAGHIPOUR F，ELLIS N，WONG C.Experimental and computational study of gas solid fluidized bed hydrodynamics[J].Chemical Engineering Science，2005，60（24）:6857-6867.

[14]BARRASSO D，TAMRAKAR A，RAMACHANDRAN R.A reduced order PBM ANN model of a multi-scale PBM DEM description of a wet granulation process[J].Chemical Engineering Science，2014，119（119）:319-329.

[15]侯广信，陈建义.颗粒碰撞团聚对旋风分离器分离性能影响研究[J].石油机械，2008，36（5）:1-4.

[16]MCGRAWR.Description of aerosol dynamics by the quadrature method of moments[J].Aerosol Science&Technology，1997，27（2）:255-265.

[17]耿县如，徐庆，李占勇，等.喷雾冷冻法单个液滴冻结过程模拟[J].化工进展，2012，31（5）:981-986.