基于确定性等价收益的风险决策方法研究及案例分析

李新运，刘 君，杨志恒

(1.山东财经大学 管理科学与工程学院，山东济南 250014；2.山东财经大学区域经济研究院，山东济南 250014)

一、引 言

风险决策问题一直是管理学、心理学和经济学非常关心的未解之谜[1-2]。决策是一个过程，该过程是为实现某种目标而对未来一定时期内有关活动的方向、内容及方式的选择或调整[3-4]。因此，科学有效的风险决策评价方法是风险决策成败的关键。

迄今为止，得到广泛应用的基本风险评价准则是期望值准则，该准则由Neumann和Morgenstern[5]在Bernoulli的“圣彼得堡悖论”[6]基础上提出，其判据是方案条件结果的期望或者期望效用值。随着风险评价问题的日益复杂化，该准则呈现出较多的不足之处[7-8]：只考虑了方案的收益性，仅仅从收益这个方面来评价各个方案的优劣，并进行排序，而没有考虑决策者对决策结果所发挥的重要性、关键性作用，也就是说没有反映出决策者对待风险的态度。而确定性等价收益模型的提出，弥补了基本风险评价准则存在的不足。该模型常被应用于委托代理领域，由期望收益减去风险成本计算得到[9]。由此可见，该模型综合考虑了收益与风险两个因素，且模型中的风险成本函数与体现参与人风险态度的绝对风险规避度[10-11]紧密联系。然而，参与人作为决策主体，他们选择策略的目标是效用最大化[12-13]，因此，用效用函数对收益函数进行替代，更加符合客观实际。对于效用函数的构建，学术界的讨论较为少见[14-15]，姜青舫给出一条可用于更广泛情形的定理，这条定理证明，递减的风险厌恶效用函数可一般地由定常或递减的风险厌恶效用函数经有限次相加而构成；韩中庚给出了风险喜好型和风险厌恶的非线性效用函数的构造，并给出了两类函数的构造方法。

为了更加准确地表达风险对决策结果的影响，本文选取确定性等价收益作为评价模型，对风险决策问题进行研究；同时，创新性地利用风险规避度函数对效用函数进行推导，使风险态度在决策过程中得到更为合理准确的量化；并根据计算得到的确定性等价收益值进行方案排序。最后，利用山东半岛蓝色经济区各县区的数据进行案例分析，研究结果表明，确定性等价收益模型及本文基于风险规避度函数推导得到的效用函数，具有较大的理论意义与应用价值。

二、确定性等价收益评价模型简介

随机性收益的确定性等价收益CE，就是把随机性收益转变为期望收益E(x)，并扣除风险成本RC。具体公式表示如下：

由公式可知，确定性等价收益值越高，对应的决策方案越好。该决策模型既考虑了实际问题的期望收益，也考虑了其中的风险成本，是一个对收益与风险进行综合衡量的风险决策模型。因此，在实际决策过程中，采用该模型作为评价模型，对各个决策方案进行评价，会得到更为合理准确的评价结果。

在实际决策问题中，经常会包含许多随机因素或者不确定因素。因此，随机决策有两个基本特点，即决策的随机性与决策结果值的效用特征[8]。决策问题的每种结果对于决策者都有一定的效用，即在有风险的情况下决策人对每种方案的决策结果是有偏好的[12]。为考虑效用这一特征，本文将公式(1)中的期望收益E(x)看作期望效用u(x)，即将初始收益决策矩阵通过效用函数转化为对应的效用决策矩阵，进而对各方案的确定性等价收益进行计算，筛选出最优方案。

(一)效用函数

在消费者行为中，效用函数通常用来表示消费者在消费中所获得的效用与所消费的商品组合之间数量关系的函数，以衡量消费者从消费既定的商品组合中所获得满足的程度；在投资者行为中，效用函数用来表示投资者所获得的效用与得到的投资收益之间数量关系的函数，以衡量投资者从投资收益中所获得满足的程度。同时，用不同类型的效用函数也可以表征决策者对风险的不同态度[8]。常用的几个效用函数如下：

公式(2)中，当α＜1，α＝1，α＞1时，分别表示决策者为风险规避、风险中立、风险喜好型的；公式(3)、(4)具有不变的绝对风险规避度ρ(后文有具体推导)，且当ρ＞0，ρ＝0，ρ＜0时，分别表示决策者为风险规避、风险中立、风险喜好型的。

(二)风险成本函数

风险成本表示投资者感觉到的以货币单位表示的风险损失，表示如下：

式中，ρ为绝对风险规避度，表示主观上对风险的态度；σ2为收益x的方差，表示客观上风险程度的高低。在金融经济学、证券投资学里面，风险成本一般称为风险溢价或风险报酬。

(三)风险规避度函数

效用函数与风险成本函数中提到的绝对风险规避度ρ，与相对风险规避度ρr总称为风险规避度[16]。相对风险规避度(相对风险规避系数)在解决实际问题时较少使用，这里重点对绝对风险规避度进行介绍。

Arrow[10]和Pratt[11]提出风险厌恶理论，并定义了绝对风险规避度，即为

公式(5)中，当ρ＞0，ρ＝0，ρ＜0时，分别风险规避、风险中立、风险喜好。且ρ值越大，意味着风险规避程度越高，决策者越害怕风险。

三、根据绝对风险规避度函数求解效用函数

通常情况下，已知效用函数就可以根据定义求出绝对风险规避度函数。但是，在现实情况中，风险规避函数比效用函数更能准确直观地体现决策者在决策时对待风险的态度。所以，根据给定的风险规避度函数求解出对应的效用函数，具有理论分析和实际应用方面的需要。然而，现有的相关研究很少涉及该过程的推导，因此下文将对该求解过程进行进一步的阐述。

根据绝对风险规避度的定义公式(6)，可以得到二阶微分方程u″(x)+ρ(x)u′(x)＝0。 为了降阶，令v＝u′，微分方程变为：v′(x)+ρ(x)v(x)＝0。对降阶后的微分方程分离变量，得到dx。求解分离变量后的微分方程得到

最终，得到效用函数

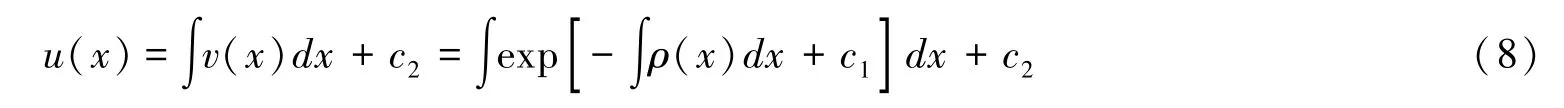
由公式(8)可知，要想求出具体的的表达式，需要给出绝对风险规避度函数的具体表达式，不失一般性，假定幂函数型的绝对风险规避度函数为

式中，参数取值范围的确定原则是假定投资者为风险规避或风险中性的，即绝对风险规避度随着收益值的增加而减小，即收入越高越不害怕风险[9]。根据参数b的取值不同，分两种情况进行讨论。

(1)当b＝-1时，此时有

再根据a＝1和a≠1，分两种情况进行分析如下。

①如果a＝1，根据(8)式得到u(x)＝ec1lnx+c2。

根据边界条u(1)＝0，u(xm)＝1，得到所以有最后得到归一化的效用函数为

②如果a≠1，同理可得归一化的效用函数为

(2)当b≠-1时，此时有则效用函数为

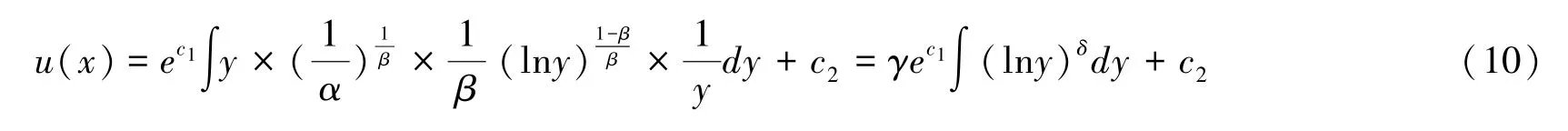
根据参数b的具体取值，分3种情况进行求解。

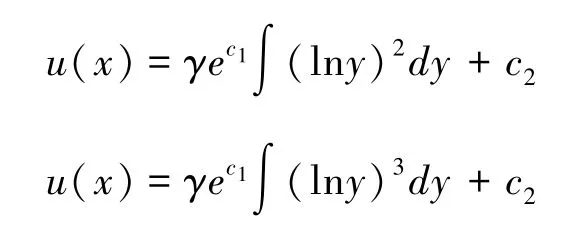
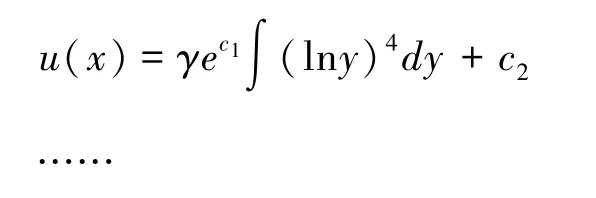
这些具体的效用函数可以根据下面的两个不定积分公式

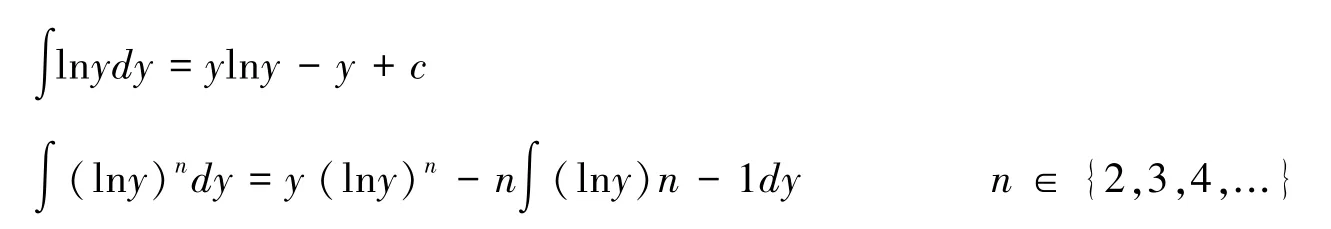
分别求解出来，这里不再赘述。只是此时得出的效用函数表达式更加复杂，更加偏向于理论意义。另外，对于指数型的绝对风险规避度函数ρ(x)＝aebx(a＞0，b≤0)，也可以根据(7)、(8)两式进行类似的分析。

四、案例分析

本文以山东半岛蓝色经济区7个地市54个县区的数据进行验证。由于滨州只有无棣、沾化两个县区位于蓝色经济区范围内[17]，为便于最后的比较分析，本文选取滨州整个地市所有县区的数据进行研究。所用数据取自2016年《山东统计年鉴》，为使数据之间横向可比，本文采用相对指标。按照人均固定资产投资完成额(T)情况进行投入方案的划分，选取规模以上工业企业利税总额占主营业务收入比重(C)来衡量各县区的产出状态，从而构造出收益决策矩阵。再根据给定的三种风险规避度函数，求解对应的效用函数，得到效用决策矩阵。最后，计算得到各方案的确定性等价收益值，并据此进行方案排序。

(一)构建收益决策矩阵

按投入指标T水平高低，将各县区划分为三个等级，作为三种投入方案a1，a2，a3，a1，a2，a3分别表示人均固定资产投资完成额低于50 000元/人、50 000～100 000元/人、高于100 000元/人；然后，按产出指标C的大小分为三种产出的自然状态θ1，θ2，θ3。产出状态θ1，θ2，θ3分别表示规模以上工业企业利税总额占主营业务收入比重低、中、高三种情况。表中θ1，θ2，θ3分别表示三种自然状态，p1，p2，p3分别表示三种自然状态的概率，下文同。

各投入方案不同产出状态所包含的县区如表1所示。

表1 各县区所属投入方案及产出状态

每一投入方案每种产出状态下各县区的产出水平求均值，作为各方案在不同产出状态下的条件收益值。如表2所示。

表2 收益决策矩阵

(二)方案评价

如前文所述，进行方案评价时，首先要给定该风险决策问题的绝对风险规避度函数，进而求出每一风险规避度函数对应的效用函数，根据效用函数将原收益决策矩阵转化为效用决策矩阵，计算出各个方案对应的确定性等价收益值，据此进行比较排序，筛选出最优方案。

本文对风险规避度函数分三类进行假设，包括风险规避度恒为0、风险规避度恒为常数a(a＞0)及风险规避度函数为一般形式，即ρ(x)＝axb，a＞0，b＜0。

(1)风险规避度为0。此时，决策者对待风险的态度为风险中立，即ρ＝0，则α＝1，效用函数为u(x)＝cxα＝cx，c＞0。这里假设c＝1，得到效用函数u(x)＝x，即条件收益值即为效用值，效用决策矩阵与收益决策矩阵相同。此时，各方案的确定性等价收益值如表3所示。表中，E(x)、RC、CE分别表示各方案的期望效用值、风险成本、确定性等价收益，下文同。

表3 方案效用决策矩阵及确定性等价收益得分

从表3中可以看出，当风险规避度为0，即决策者对风险保持中立态度时，风险成本RC为0，各方案的确定性等价收益值即为对应的期望效用值。最终得到的方案排序从优到劣表示为a3＞a2＞a1。即不考虑风险因素时，固定资产投入越多，经济产出效果便越好。

(2)风险规避度为a(a＞0)。此时，决策者对风险持有规避态度，且规避程度始终不变，即ρ＝a(a＞0)。同时，b＝0，按前文推导可知，此时效用函数为u(x)＝1-e-ax。若假设a＝1，得到效用函数u(x)＝1-e-x，风险成本函数各方案的效用决策矩阵及确定性等价收益值如表4所示。

表4 方案效用决策矩阵及确定性等价收益得分

分析表4可以知道，当决策者对待风险的态度是风险规避时，每个方案均存在一定的风险成本。此时，确定性等价收益值不再简单的等于期望效用值，而成为期望效用值与风险成本之差，所以，最终的决策结果不仅仅对效用进行考量，更考虑到了风险成本这一因素。所以，此时的方案排序会发生变化，变为a1＞a2＞a3。在风险规避程度为0时筛选出的最优方案a3，此时却成为最劣方案。

显然，固定资产投入越高，投资者承担的风险便越大，因此当考虑风险因素时，原本最优但风险最大的方案a3，此时便成为最差的投入方案。且经验证，当a取值为0.1、0.5、0.8时，方案排序均为a1＞a2＞a3。由此可见，此评价结果较为稳定，且符合客观实际。

(3)风险规避度函数为一般形式，即为ρ(x)＝axb，a＞0，b＜0。此时，决策者同样是风险规避的，但对风险的规避程度随着收益值x的变化而变化。本文假设值得注意的是，此时风险成本函数为每个方案的风险成本不再是简单的一个常数，而应为由风险成本矩阵计算得到的期望风险成本。按前文推导可知，此时效用函数为故而得到各方案效用决策矩阵与确定性等价收益值如表5所示。

表5 方案效用决策矩阵及确定性等价收益得分

由于此时效用函数发生变化，且每个方案的风险成本不再是固定的常数而与收益值密切相关，所以与表4相比，表5中各方案的期望效用与风险成本均发生改变，方案的最终排序也不一致，此时为a1＞a3＞a2。且当a取值为 0.1 时，方案排序仍为a1＞a3＞a2；而当a取 0.5、0.8 时，方案排序变为a1＞a2＞a3。

(4)结果总结。分析各方案在设计的三种风险规避度函数下的排序结果可以看出，当决策者对待风险的态度不同时，会导致不同的决策结果。

当为风险中立时，即忽略风险因素的影响，此时风险成本为0，最终每一方案的确定性等价收益值即为期望收益值，得到的方案排序为a3＞a2＞a1；当为风险规避时，本文又分为两种情况进行分析，第一，风险规避度恒为大于0的常数，此时考虑了风险成本，但决策者对待风险的规避程度始终不变，最终得到a1＞a2＞a3的方案排序；第二，风险规避度函数是一般形式，即随着收益值x的增大，风险规避程度减小，决策者对待风险的规避程度是不断变化的。此时，最终的方案排序随着常数a取值的不同而不同。

五、结论与启示

本文以山东半岛蓝色经济区各县区数据为例，以确定性等价收益为评价模型，创新性的从风险规避度函数出发，对相应的效用函数进行推导，最终计算得到各方案的确定性等价收益值，据此进行方案排序。在三种不同的风险规避度函数下，计算得到了不同的评价结果，分析该结果，得到的结论与启示如下：

(1)成立专门的风险评估机构，降低政策的风险成本。对决策方案进行评价时，要综合考虑收益与风险两个因素，且对于风险因素，决策者风险态度不同，会导致不同的决策结果。由案例分析结果可知，当决策者对待风险的态度分别为风险中立、风险规避时，筛选出的最优方案是不同的，且最终的方案排序差距较大。所以，针对蓝色经济区以及其他相关地区的政府决策，进行风险与收益评估，是十分必要的；(2)建立相应的测评小组，对决策者的风险态度进行准确合理的量化。在决策过程中需要考虑风险因素，同时参与人作为决策主体，其风险态度发挥的重要作用同样不容忽视，因此对决策者的风险态度进行准确合理的量化也是十分重要的；(3)应基于变化的风险规避度，对政府决策风险进行测度。风险规避的决策者，其对风险的规避程度变化状态不同，会导致不同的决策结果。案例分析结果表明，当决策者对待风险的规避程度始终不变时，得到的方案排序，与风险规避程度不断变化时得到的方案排序存在一定的差异。而在实际决策过程中，风险的规避程度往往不是一成不变的。因此，蓝色经济区相关政府机构进行决策过程中，要依据变化的风险规避度对风险加以衡量，以筛选出最符合实际的决策方案。

本文选择的评价模型即确定性等价收益模型，综合了收益与风险两个因素，同时，由风险规避度函数推导出来的效用函数，对风险决策态度体现得更为准确细致，得到的研究结果符合客观实际。因此，本文的研究方法具有较大的创新性与应用价值。但由于客观条件限制，本文在利用风险规避度函数推导效用函数过程中，对b≠-1时，只考虑了取值有一定规律性的情况，对其他取值情况，有待进一步的研究。

[1]李纾，毕研玲，梁竹苑，等.无限理性还是有限理性?——齐当别抉择模型在经济行为中的应用[J].管理评论，2009(5)：103-114.

[2]李新运，任栋.多目标下的投资项目风险评价方法与实证研究[J].科研管理，2012(5)：101-106.

[3]王庆，陈果，刘敏.基于价值-决策双准则的风险决策理论[J].中国管理科学，2014(3)：42-49.

[4]PREM K P， NG D， PASMAN H J， et al.Risk Measure Constituting A Risk Metrics Which Enables Improved Decision Making：Value-at-risk[J].Journal of Loss Prevention in the Process Industries， 2010，23(2)：211-219.

[5]VON NEUMANN J， MORGENSTERN O.Theory of Games and Economic Behavior[M].Princeton N J：Princeton University Press，1944.

[6]BERNOULLI D.Exposition of A New Theory on the Measurement of Risk[J].Econometrica， 1954，22(1)：23-36.

[7]袁捷敏.三种风险型决策评价准则及其关系[J].统计与决策，2009(18)：136-137.

[8]赵新泉.管理决策分析(第三版)[M].北京：科学出版社，2014.

[9]张维迎.博弈论与信息经济学[M].上海：上海三联书店，2004.

[10]PRATT J W， Risk Aversion in the Small and in the Large[J].Uncentainty in Econometrica， 1978， 44(2)：420-420.

[11]ARROW K J， Essays in the Theory of Risk-bearing[M].Amsterdam：North-Holland， 1970.

[12]李保明，刘家壮.效用函数与纳什均衡[J].经济学家，2000(4)：21-28.

[13]MACHINA M J， Expected Utility Analysis Without the Independent Axiom[J].Econometrica， 1982， 50(2)：227-323.

[14]姜青舫.关于构造效用函数的一个新定理[J].运筹学杂志，1990(2)：45-46.

[15]韩中庚.非线性连续型效用函数的构造方法及其应用[J].运筹学学报，2007(5)：257-261.

[16]HIBBARD B.Model-based Utility Functions[J].Journal of Artificial General Intelligence.2012， 3(1)： 1-24.

[17]苟露峰，高强.山东省海洋产业结构演进过程与机理探究[J].山东财经大学学报，2016(8)：43-50.