GPS定位中产生的误差对变形监测影响的分析

（将乐县煤炭行业管理办公室， 福建 三明 353300）

0 引言

1990年代后，GPS卫星定位和导航技术与现代通信技术相结合，在空间定位技术方面引起了革命性的变化。其定位的绝对或相对精度从m级扩展到cm级、mm级乃至亚mm级，从而大大拓宽了它的应用范围。但利用GPS定位技术进行变形监测时，由于伪距单点定位、载波相位测量和整周跳变等数据都是基于一个时间段里的观测数据，在观测时段上，从测站上开始搜索、接收卫星信号起至停止观测间的连续工作时间段，不同等级的GPS测量对观测时段长度有不同的要求，同时在不同时间段及不同仪器观察的数据所产生的误差而也不尽相同，因此 GPS定位中产生的误差对变形监测的数据精度有一定的影响。而其定位数据精度受卫星星历误差、卫星钟钟差、对流层延迟、电离层延迟、多路径误差、接收机钟钟差、接收机的位置误差、接收机测量噪声以及数据处理软件本身的质量等多种误差的影响，在数据处理传输过程中，还将涉及周跳的探测及修复、整周模糊度的确定等一系列误差影响。这些误差在GPS定位中都不可避免的产生，而其各种误差都将或大或小对变形监测产生影响，对于变形体本身来说，GPS周期性变形监测中的两期观测数据的坐标差是对形变体本身的形变反应还是GPS观测误差的反应，这就很难确定了。

因此，只有掌握GPS定位原理，理解这些误差源的性质及其影响，才能在制定出更好的技术方案和作业方式，更好的消除和减弱GPS定位中各种误差的影响，提高GPS定位观测的数据成果的准确性和精确性，从而使GPS定位技术在各种变形监测中更加广泛的应用。

1 GPS定位原理

1.1 伪距测量原理

在伪距测量中，GPS观测过程中时间误差传递的影响原理如下：假设用户的位置己知为(Xk, Yk, Zk)，在该点设置一台GPS接收机，tk时刻观测卫星Si的伪距考虑卫星钟钟差、电离层和对流层延迟、时间测量随机误差等，必须引入各种误差改正，所以得到观测方程如下：

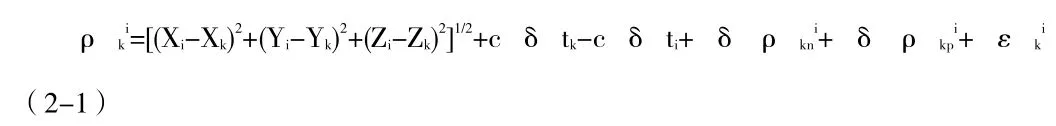
式（2-1）中δtk表示接收机钟差，δti表示卫星钟差，表示电离层折射影响，δρkp

i表示对流层折射影响，(Xi，Yi，Zi)表示卫星在ti时刻的位置坐标。由于通过GPS接收机的基本观测量仅能得到时间延迟τ，无法得到信号的发射时间ti，因此必须由接收时间tk算出ti, ti=tk-d/c，然后根据卫星导航电文所给出的卫星星历参数可以计算出ti时刻的卫星位置坐标(Xi，Yi，Zi)，因此从卫星到接收站的距离就可通过计算得到，再根据导航电文中给出的卫星钟差改正、电离层和对流层延迟改正等参数，修正观测方程中的误差项，这样式（2-1）中的未知量仅剩下本地时钟误差δtk一项，因此从原理上讲，仅观测一颗GPS卫星就可实现时间传递，而同时观测多颗卫星则可以提高时间传递的精密度。

1.2 绝对定位原理

GPS绝对定位是一个用户利用GPS接收机，以地球质心为参考点，对卫星信号进行接收和观测，确定接收机天线在WGS-84坐标系中的绝对位置，又称单点定位或伪距定位。

绝对定位的基本原理是以GPS卫星和用户接收机天线之间的距离（或距离差）观测量为基础，根据已知的卫星瞬时坐标，来确定接收机天线所对应的点位，即观测站的位置。GPS绝对定位方法的实质是测量学中的空间距离后方交会。有动态绝对定位和静态绝对定位两种方式，且动态绝对定位中一般采用测码伪距定位法。

对利用伪距进行单点定位时，一般要同时观测4个卫星信号，由式（2-1）即可建立起相应的方程组，解算该方程组可得到测站i的位置参数和相应时刻的接收机钟差。因此只要同时保持4个以上的卫星观测值即可进行单点定位。

1.3 相对定位原理

GPS相对定位是利用两台或两台以上GPS接收机分别安置在不同的GPS点上，并同步观测相同的GPS卫星，将所获得观测值按一定的方法进行差分处理，消除一些误差对各观测值影响的相关部分，然后再进行解算，可以获得GPS点间的相对位置或基线向量，GPS相对定位也叫差分GPS定位(如图2-2所示为GPS相对定位原理示意图)。根据观测模型有卫星间求差分模型、测站间求差分模型、历元间求差分模型三种，根据其信息的发送方式可分为伪距差分、相位差分及位置差分等。在GPS观测中各种差分均由基准站发送改正数，由用户站接收并对其测量结果进行改正，以获得精确的定位结果，GPS差分定位技术也是目前GPS测量中定位精度最高的定位方法。

2 GPS定位中的各种误差源

在GPS定位系统中，需要利用遥测信号到达测量站的时间来计算目标的位置，由于是以时间来定位，因此需要将卫星钟和接收机钟同步到某一时间基准上，同时要求观测得到的时间的精密度要高，因为它将直接影响到定位解算是否准确，要求各测量站时钟之间要高精度的时间同步，其不同步误差将直接造成测量误差，且要求各测量站间能实现纳秒级的时间同步。在GPS测量过程中的主要误差来源在GPS卫星、卫星信号的传播过程和地面接收设备，同时在高精度的GPS测量中,还应注意到与地球整体运动有关的地球潮汐、负荷潮及相对论效应等影响。

2.1 与卫星有关的误差

2.1.1 卫星星历误差

卫星星历误差是指卫星星历给出的卫星空间位置与卫星实际位置间的偏差，由于卫星空间位置是由地面监控系统根据卫星测轨结果计算求得的，所以又称为卫星星历误差。它是一种起始数据误差，其大小取决于卫星跟踪站的数量及空间分布、观测值的数量及精度、轨道计算时所用的轨道模型及定轨软件的完善程度等。

2.1.2 卫星钟误差

在实际观测中，GPS时间系统必须由地面监测系统来确定和保持，地面监测系统测出卫星时钟与GPS标准时之间的偏差，并通过导航电文发送给用户，用户用导航电文中的钟差改正参数修正卫星信号发射时刻的偏差，卫星钟的这种偏差可用如下的二阶多项式进行改正：

式（3-1）中，toe为卫星钟修正的参考历元，a0、a1、a2为卫星钟的钟差、钟速及钟速变化率。经过这样的修正，各卫星的时钟与GPS标准时的偏差可以保持在20ns，由此引起的等效距离偏差不会超过6m，但是在美国实施SA技术以后精密度大为降低。在相对定位中，经过改正后的卫星钟误差残余误差可通过观测量求差(或差分)的方法消除。

2.1.3 相对论效应

相对论效应是由于卫星钟和接收机钟所处的状态(运动速度和重力位)不同而引起卫星钟和接收机钟之间产生相对钟误差的现象。在狭义相对论的影响下，卫星钟比静止在地球上的同类钟走的慢，而在广义相对论的影响下，卫星钟比静止在地球上的同类钟走的快，因此在狭义和广义相对论的影响下，钟安放在卫星上比安放在地面上要快，为消除这一影响,一般将卫星钟的标准频率减小4.5×10-3Hz。

2.2 传播过程中有关的误差

2.2.1 电离层误差

在地球上空距地面 50km-100km之间的电离层中，气体分子受到太阳等天体各种射线辐射产生强烈电离，形成大量的自由电子和正离子。当GPS信号通过电离层时，与其他电磁波一样，信号的路径发生弯曲，传播速度也会发生变化，从而使测量的距离发生偏差，这时用信号的传播时间乘上真空中光速得到的距离就不会等于卫星至接收机之间的几何距离，从而产生电离层延迟误差，这种偏差称为电离层折射误差。

电磁波经过电离层由于折射率n的变化引起的传播延迟量δp=∫(n-1)ds ,由大气物理学的折射公式可以得到时间延迟：

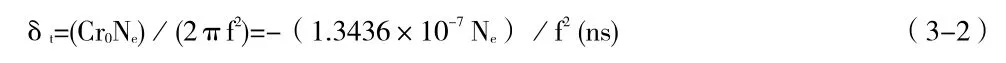
式(3-2)中f为观测频率，C为光速，Ne为传播路径上的电子总含量，r0为经典电子半径。由式(3-2)可知电磁波在电离层中产生的各种延迟与电磁波传播路径上的电子总量有关。假设在1986年5月23日16时观测，其电子含量为5×1011个，其观测频率为1500MHZ时，即该时刻的观测的电离层时间延迟δt为2.2ns。

2.2.2 对流层误差

对流层延迟是电磁波信号通过对流层时其传播速度不同于真空中光速所引起的。地球表面上约20km-50km的大气层称为对流层。与电离层一样，电磁波在穿过对流层时GPS信号产生折射，从而引起对流层上的传播延迟。由于对流层距地面很近，大气的状态受地面气候的影响很大，且对流层随纬度和高度的变化呈现出很大的变化，而且随时间变化也非常快，因此在GPS观测中，不同时间段观测的时间延迟是不一样的，因此对流层误差也有所不同。

2.2.3 多路径误差

由于接收机周围环境的影响，卫星信号(反射波)将会通过若干条路径（间接路径）到达进入接收机天线，因此到达接收机的各条射线经历的传播时间不同，这使得接收机所收到的信号中含有各种反射和折射信号的影响，这种由于多路径的信号传播所引起的干涉时延效应就被称作多路径效应。对于载波信号来说，其波程差Δ使地面反射波中的伪噪声码比直接波中的伪噪声码增加一个时延：

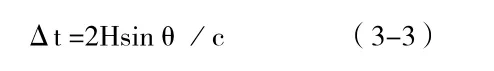
式（3-3）中H为天线离地面的高度，θ为观测仰角，假设天线离地面的高度H为1.5m，观测仰角θ为45。，这种情况下由多路径产生的时间延迟Δt为7ns，相当与距离误差为2.1m。

2.3 与接收机有关的误差

2.3.1 接收机钟误差

接收机的钟面时与GPS 标准时之间的差异称为接收机钟差。GPS 接收机一般采用高精度的石英钟，其精度约为 10-9，远达不到原子钟 10-15的精度，若接收机钟与卫星钟间的同步差为1μs，由此产生的等效距离误差约为300m。为了更好的消除由接收机钟引起的误差，可把每个观测时刻的接收机钟差当作一个独立的未知数，并认为各观测时刻的接收机钟差间是相关的，在数据处理中与观测站的位置参数一并求解，从而减弱接收机钟差的。

2.3.2 接收机的位置误差

相位中心随着信号输入的强度和方向不同而有所变化，这种差别叫天线相位中心的位置偏差，这种偏差的影响可达数毫米至厘米。而如何减少相位中心的偏移是天线设计中的一个重要。为了减少天线相位中心位置偏差的影响,要求我们安置天线时要以天线附有的方位标进行定向，同时使用性能好的天线(如扼流圈天线)，以求尽可能的减少相位中心位置偏差带来的误差。在实际工作中若使用同一类天线，在相距不远的两个或多个测站同步观测同一组卫星，可通过观测值求差来减弱相位偏移的影响。

2.3.3 周跳

在实际观测条件下，接收机往往会由于某种原因(如卫星信号被挡住)对卫星短时间失去跟踪，在失去跟踪时间内相位的变化就不能被测出，即载波相位的小数部分是连续，而其整周数不再连续，因此称为失周或失锁，也称为周跳。在短距离 GPS 基线定位中，大气轨道误差基本被抵消，电离层和对流层延迟由于它们的相关性也消除了大部分影响，失周大小能保持较好的整数特性，较容易处理。

2.4 其他因素误差

在高精度的GPS测量中，除了上述三类误差外，还有其它的一些误差来源，如地球自转和地球潮汐，对GPS定位也会产生一定的影响。

在协议地球坐标系中，如果卫星的瞬时位置是在信号发播的瞬时计算的，那么还应考虑地球自转的改正。因为若某一时刻卫星从该瞬时空间位置向地面发射信号，当地面接收机接收到卫星信息时，与地球固联的协议坐标系相对于卫星发射瞬间的位置已产生了旋转。这样，接收到的信号会有时间延迟Δt，这个延迟与地球自转速度有关。若地球自转速度Δt时间内旋转的角度为

式（3-4）中Δτij可为卫星信号传播到观测站所需的时间，因此地球自转的时间延迟将引起坐标系中的坐标微小误差。消除地球自转的影响的误差可通过对测站或卫星位置进行改正的方式来对测站位置进行改正。

根据以上分析，现将GPS定位中伪随机码（C/A码）捕获的载波信息中主要误差引起的相对偏差值列于表1。

表1 GPS定位中主要误差引起的相对偏差值

3 GPS定位中产生的误差对变形监测的影响

利用GPS进行变形监测的作业方式可分为周期性和连续性模式。在周期性GPS静态相对定位的变形监测中，其GPS定位精度与基线边长、时段长度、仪器性能、多径干扰、卫星星历、电离层延迟、对流层延迟、天线相位中心变化、基线解算、各项观测误差的模型误差以及监测网平差方法等众多因素有关。当几期位移量变化很微小时可适当延长其观测周期，以便能更好的观测变形体的真正变形量，即观测时间间隔的长短确定对变形监测也具有一定的影响。

在一般的GPS变形监测中观测者关注的是两期的变形量数据，而不是变形监测点本身的坐标，但在GPS周期性变形监测中各点的两期坐标差不可避免的含有系统误差或偶然误差，那么在监测数据中便包含了GPS定位中产生的误差值，从而影响了监测的准确性，特别是对于监测点的变化量较小的，其两期变化量是由GPS定位中产生的误差的反应，还是点位真正的变形量引起的便难以判断了。

3.1 GPS定位中产生的误差对GPS数据的影响的分析

在地形起伏不大的平坦地区,当点之间的距离不大时,可以认为两点的高程异常相同或非常小，可以忽略不计，这样就可以采用两点之间的GPS大地高差代替正常高高差。

现以GPS沉陷变形监测为例[2]。监测区域有6个监测点，测线全长403 m。GPS监测的同时也采用附合水准路线按三等水准要求对6个点进行观测。水准测量所得各点高程和用GPS测量经无约束平差后所得的高程，见表2为水准测量高程与GPS测量高程的比较。

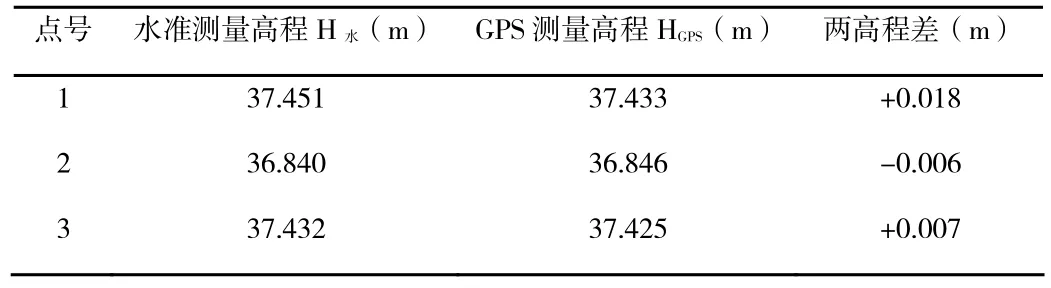
表2 水准测量高程与GPS 测量高程的比较

?

传统的水准测量对于高程测定具有较高的精度，所以水准测量所得的高程与GPS测量经无约束平差后所得的高程差值△H= H水-HGPS即是GPS测量高程中含有误差的反应，其误差可能由于GPS定位中产生的误差和数据处理过程中产生的误差（无约束平差中产生的误差对数据影响较大）。因此考虑到水准测量中误差的影响，其个别观测点（如1、4点）的水准测量结果与GPS观测结果的高程差存在较大差值主要是因为GPS定位中产生了误差，由此可知GPS定位中产生的误差对GPS测量的数据有一定的影响。

3.2 GPS定位中产生的误差对变形监测水平位移影响的实例分析

相邻两周期某个水平位移监测点是否为显著性的变形，即该点水平位移变化量到底是由观测误差所引起的，还是点位真正的变形引起的，必须对其进行区分。下面便以GPS定位在某监测网变形监测中平面位移变形的数据[5]为例，分析相邻两周期各点水平位移监测点的稳定性及由GPS定位中产生的误差对各点稳定性的误判。该次实验使用的是Trimble 5700系列双频GPS接收机，标称精度为5mm+1ppm。

根据方案对该网进行观测，并对观测数据进行平差处理，如图 1为水平监测网网型图。GPS对该监测网中各点的水平位移的两期网点坐标及坐标差监测成果见表3。

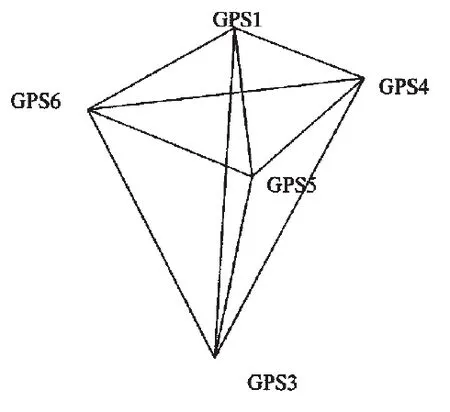
图1 水平监测网网型

表3 GPS对各监测点水平位移的两期网点坐标及坐标差统计表

表4 水平位移监测点稳定性分析成果表

从表3的两期坐标差来看，中误差均较小，因此GPS定位在水平位置上具有较高的精度，但还是有必要对该监测网各点的稳定性做出判断。根据平均间隙法[6]及从位移变化量的大小可知GPS3点在X轴发生了位移。通过显著性分析法[7]，当△x≥3m△x、△y≥3m△y时，可认为该监测点在相邻两周期有“较大位移”；当3m△x≥△x ≥2m△x、3m△y≥△y≥2m△y时，可认为该监测点在相邻两周期有“显著位移”；当 2m△x≥△x≥m△x、2m△y≥△y≥m△y时，可认为该监测点在相邻两周期有“有位移趋势”；否则可认为该监测点相邻两周期“没有位移发生”，即该监测点相邻两周期的高程变化量不是变形引起的，可能由两期观测中出现的误差的影响，表 4为各点水平位移监测点稳定性情况。

3.3 GPS定位中产生的误差对变形监测垂直位移影响的实例分析

表5 GPS大地高变形量与水准测量变形量比较差值（mm）

在GPS 定位技术中，其观测数据在水平方向上的精度已相对较高，而其数据精度在垂直方向上稍微较弱。本例采用GPS定位技术对某边坡进行变形监测[8]，该监测采用4 台Trimble 5700 型GPS接收机进行观测，GPS接收机天线采用强制对中设站，用Trimble 5700型GPS接收机随机所带的平差软件TGOffice 进行基线解算，采用了GPSADJ软件进行网平差，以C、D 两点的坐标为起算数据。同时,用Ⅱ等几何水准测量各监测点的垂直位移量。GPS变形监测网的布设如图4 所示, 为了更好的监测边坡的稳定性，须选取一定参考点作为的基准点，图3中A 、B 、C 、D为边坡区外的监测基准点（四个基准点都相对稳定），1～12 号点为变形监测点，如图2所示。

图2 GPS变形监测网

由于变形监测网点用GPS监测的同时也进行了水准测量,所以可以将GPS测得的大地高和正常高进行比较。以某一期的观测数据作为基准，表5列出了各点GPS大地高变形量△hGPS与水准测量变形量△h水的比较差值△。

上表中△ =△ hGPS-△ h水=（ HGPS＇ -HGPS） -（ H水＇ -H水）（4-1）

根据式（4-1）可得△=（H水-HGPS）-（H水＇-HGPS＇）=△H-△H＇，因为经过GPS接收机随机所带的平差软件TGOffice 进行基线解算，采用了GPSADJ软件进行网平差，以C、D两点的坐标为起算数据，其数据处理对数据误差一般较小，Ⅱ等几何水准测量中各监测点的高程是较准确的，考虑到水准测量中误差的影响，那么其个别观测点的GPS大地高变形量与水准测量变形量比较差值△存在较大差值，其主要原因是GPS定位中误差的产生，是GPS定位中产生的误差的反应。

4 结语

本文简述了GPS定位原理，可看出在其观测方程中必须加入各种必要的误差改正数，从而消除或减弱GPS定位中的误差影响；其次，特别分析了GPS定位中的各种误差源及其消除或减弱误差的方法，只有在充分了解其误差根本来源，才能更好的找出对应的方法减小误差；然后通过实例分析了GPS定位中产生的误差对变形监测水平及垂直位移的影响，从实例中可以看出GPS定位中产生的误差对变形监测数据的准确性和精确性有很大影响，那么如何减小其误差在变形监测中的影响，从而使GPS的各种优势在变形监测中得到充分发挥。

消除或减弱GPS定位中的误差，提高GPS观测精度的方法主要有以下几种:（1）提高局部GPS网基线解算的起算点坐标精度。尽量采用国家A、B级GPS网点为局部GPS网的起算点，以减小起算点误差对大地高精度的影响；（2）改善GPS星历的精度，用精密星历比用广播星历可提高精度34%，因此应建立自己的测轨系统，提供精密星历服务；（3）消弱卫星不对称对定位精度的影响,选择最佳的卫星几何图形；（4）选用双频GPS接收机,有效地消除电离层折射的延迟误差；（5）减弱多路径误差和对流层延迟误差；（6）控制点必须使用强制对中装置；（7）提高联测几何水准精度，用精密水准联测，可以有效提高GPS大地高精度；（8）提高整周模糊度的解算精度，通过实测过程中用闭合环进行检查；（9）GPS变形监测网的技术设计，包括监测网的基准设计、监测网形设计、观测时段和周期的设计及GPS一机多天线技术等的技术设计。

[1]杨小伟.GPS测量误差来源及削弱方法[J].科技资讯,2010,4:15.

[2]苗斌,刘海龙.GPS测量误差产生与修正[J].电子科学,2008,1:8.

[3]肖鸾.基于GPS的变形监测数据处理时间间隔的合理确定[J].河南理工大学学报,2008,4:414-419.

[4]王齐林.单历元 GPS变形监测数据处理理论与相关方法研究[D].中南大学,2003.

[5]王晓华,胡友健,柏柳.变形监测研究现状[J].测绘科学,2006,2:130-132.

[6]曾卫生,董键.浅谈 GPS变形监测中的误差分析与处理[J].科技经济市场,2010,4:18-19.

[7]王晓华,胡友健,柏柳.变形监测研究现状[J].测绘科学,2006,2:130-132.

[8]雷娟.GPS测量误差源分析与精度控制[J].铁道勘测与设计,2008,1:28-31.