利用焦点三角形面积公式解一类高考题

江苏省启东市汇龙中学(226200)张仁华

在解析几何中有下列两个结论:

结论1 设点P是椭圆上的任一点,F1,F2是椭圆的焦点,∠F1PF2=θ,则△F1PF2的面积

结论2 设点P是双曲线上的任一点,F1,F2是双曲线的焦点,∠F1PF2=θ,则△F1PF2的面积

根据三角形的面积公式、余弦定理及椭圆与双曲线的定义,容易证明这两个结论.

结论1证明由椭圆的定义得,PF1+PF2=2a,F1F2=2c.由余弦定理得:

所以(PF1+PF2)2-F1F22=2PF1·PF2cosθ+2PF1·PF2,即

结论2证明略.

这两个结论不仅在平面解析几何中有着广泛的应用,而且在近年的高考题中,常常有它的影子,本文试图尝试通过分类举例,希望能为大家提供一些有益的思路.

第一类,题目条件中直接出现或间接出现∠F1PF2,因而可直接利用△F1PF2的面积公式.

例1 (2009年上海卷文理科)已知F1,F2是椭圆的两个焦点,P为椭圆C上一点,且PF1⊥PF2.若△F1PF2的面积为9,则b=____.

解依题意,有可得b2=9,故有b=3.

例2 (2009年江西卷理科)过椭圆的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )

例3 (2010全国1卷文科第8题)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=( )

A.2 B.4 C.6 D.8

例4 (2010全国1卷理科第9题)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则P到x轴的距离为( )

第二类,题目条件中没有出现∠F1PF2但能求出∠F1PF2,因而也可利用△F1PF2的面积公式解题.

例5 (2003年高考北京春季第16题)如图1,已知F1,F2分别为椭圆的左、右焦点,点P在椭圆上,△POF2是面积为的正三角形,则b2的值是____.

图1

第三类,利用△F1PF2面积的多种形式作为桥梁,间接利用△F1PF2面积公式的求解.

例8 (2007年安徽理科)如图2,F1和F2分别是双曲线的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则双曲线的离心率为( ).

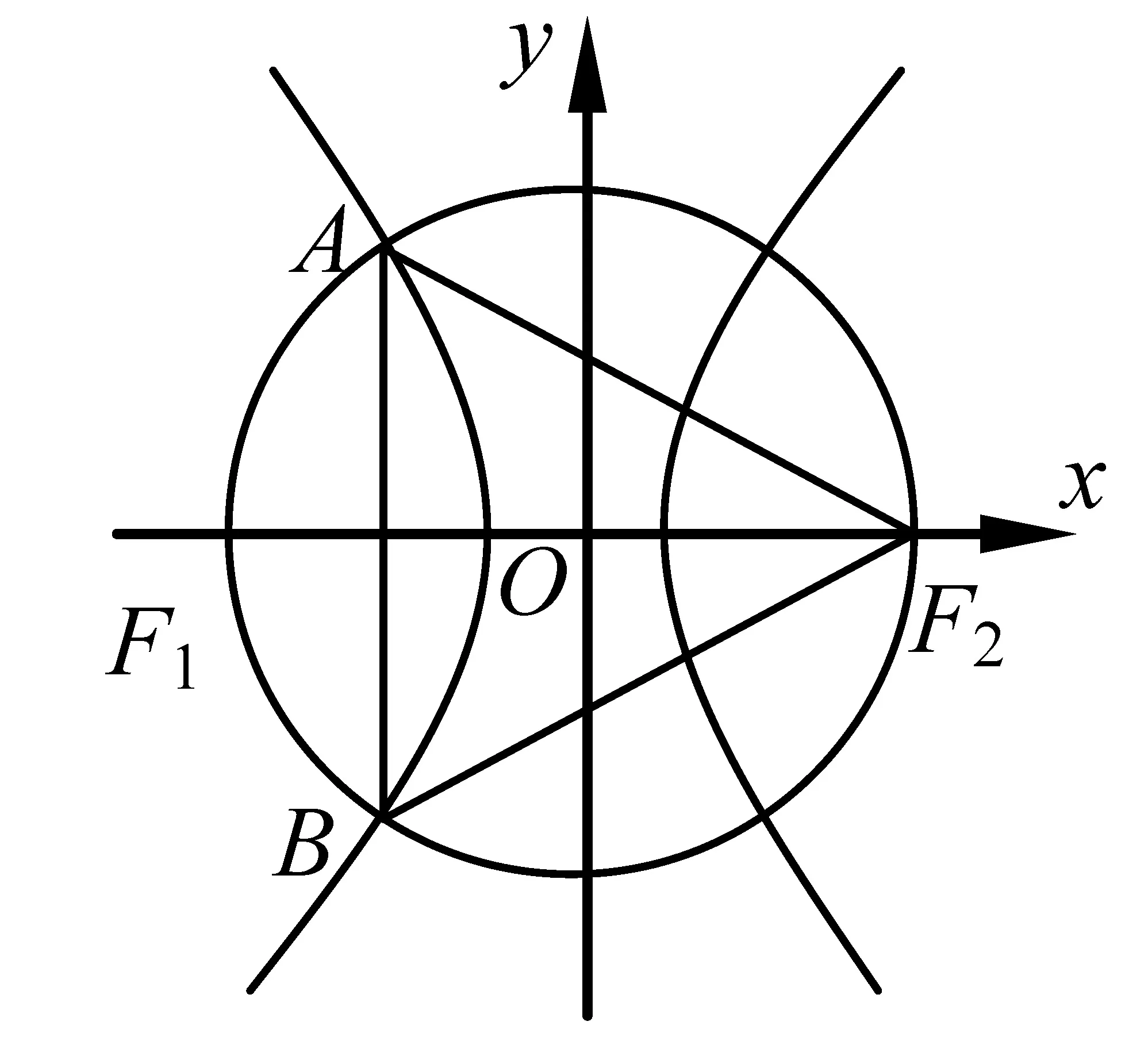
图2

(1)求实数m的取值范围;

(2)设L是相应于焦点F2的准线,直线PF2与L相交于点Q.若求直线PF2的方程.

解(1)由题设有设点P的坐标为(x0,y0),所以

因为PF1⊥PF2,由结论1:得

例10 (2014年湖北卷第9题)已知F1,F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且则椭圆和双曲线的离心率的倒数之和的最大值为( )

考点椭圆、双曲线的定义与性质,利用三角换元法求最值,难度中等.

点评将椭圆、双曲线和解三角形等知识联系在一起,重点考查椭圆、双曲线的定义与性质,充分体现了函数思想在圆锥曲线的实际问题中的应用,凸显了知识之间的联系性、综合性,能较好的考查学生的计算能力和思维的全面性、缜密性.

现在高考试卷越来越重视学生综合素质的考查,因而教师在上课时不仅要巩固三基,而且要培养学生的思维,如何发挥例题的教学功能,让学生解题时学会思考是教师值得探讨的问题.通过一些例题的总结变式,日积月累,积少成多,学生的思维能力定会不断提高.