一道高考抛物线试题的探究与推广

辽宁省抚顺市四方高级中学(113122)孟庆杰

题目(2013广东理)已知抛物线C的顶点为原点,其焦点F(0,c)(c＞0)到直线l:x-y-2=0的距离为设P为直线l上的点,过点P作抛物线C的两条切线PA、PB,其中A、B为切点.

(I)求抛物线C的方程;

(II)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;

(III)当点P在直线l上移动时,求|AF|·|BF|的最小值.

解(I)由题意,得解得c=1,所以所求抛物线方程为x2=4y;

(II)由抛物线方程x2=4y,得求导得设A(x1,y1),B(x2,y2),则以A和B两点为切点的切线PA和PB的斜率分别为所以切线PA的方程为即xx1-2y-2y1=0,同理切线PB的方程为xx2-2y-2y2=0.又两条切线PA、PB过P(x0,y0),所以x0x1-2y0-2y1=0且x0x2-2y0-2y2=0,所以A(x1,y1),B(x2,y2)两点坐标满足方程x0x-2y-2y0=0,所以所求直线AB的方程为x0x-2y-2y0=0.

(III)由抛物线定义可知|AF|=y1+1,|BF|=y2+1,所以|AF|·|BF|=(y1+1)(y2+1)=y1y2+(y1+y2)+1.联立抛物线与直线AB的方程,消去x得所以所以|AF|·|BF|=又点P(x0,y0)在直线l上,所以x0=y0+2,所以

一、纵向探究与推广

探究1 已知抛物线C:x2=2py(p＞0)的焦点为F,点M(x0,y0)为直线l:y=kx+b上的动点,直线l与抛物线不相交.过点M作抛物线C的两条切线MA、MB,其中A、B为切点.求|AF|·|BF|的最小值.

图1

解如图1,联立抛物线C与直线l方程,消y得x2-2pkx-2pb=0,因为直线l与抛物线不相交,所以判别式Δ=4p2k2+8pb＜0,即pk2+2b＜0.由上述“题目”解答,得直线AB方程为x0x-py-py0=0,联立直线AB与抛物线C方程,消x得设A(x1,y1),B(x2,y2),则由抛物线定义,得

二、横向探究与推广

探究2 如图2,已知椭圆C:的焦点为F,点M(x0,y0)为直线l:x-y-2=0上的动点,直线l与椭圆C不相交.过点M作椭圆C的两条切线MA、MB,其中A、B为切点.探究|AF|·|BF|是否有最小值.

图2

解如图2,联立椭圆C与直线l方程,消y得(2b2+1)x2-4b2x+3b2-b4=0,因为直线l与椭圆C不相交,所以判别式Δ=8b6-4b4-12b2＜0,即由上述“题目”解答,得直线AB方程为联立直线AB与椭圆C方程,消x得

所以导函数的分母Δ＜0,分母恒为正.设

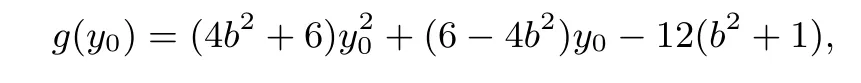
因为g(y0)的判别式所以函数f(y0)在(-∞,0)上有最大值,在(0,+∞)上有最小值,即|AF|·|BF|在区间(-∞,0)上有最大值,最大值点y0∈(-2,-1);在区间(0,+∞)上有最小值,最小值点y0∈(1,2).

探究3 如图3,已知双曲线C:的焦点为F,点P(x0,y0)为直线l:x-y-2=0上被渐近线所截的线段MN上的动点,直线l与双曲线C不相交.过点P作双曲线C的两条切线PA、PB,其中A、B为切点.探究|AF|·|BF|是否有最小值.

图3

解如图3,由题意直线l与渐近线相交,得b＜a,即因为点P在线段MN上,联立直线l与渐近线方程,求M、N点坐标得

联立双曲线C与直线l方程,消y得

因为直线l与双曲线C不相交,所以判别式Δ=-8b6+284b4-2100b2＜0,即由上述“题目”解答,得直线AB方程为联立直线AB与双曲线C方程,消x得

又x0=y0+2,所以

时,分母恒为正.设