用简单结论解高考试题*

甘肃省兰州新区舟曲中学(730087)李守明

当x1=0或x2=0时上式成立,且上式证明可逆,所以结论成立;焦点在y轴上时,结论仍然成立.

例1 (2008年高考辽宁理科数学20题)在直角坐标系xOy中,点P到两点的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.

(1)写出C的方程;(2)若求k的值.

解(1)略;(2)设D(x0,y0),直线Q1Q2的方程为mx+ny=1,因为OD⊥Q1Q2,垂足为D,所以

D(x0,y0)在直线Q1Q2上,

又OQ1⊥OQ2,根据结论1,则

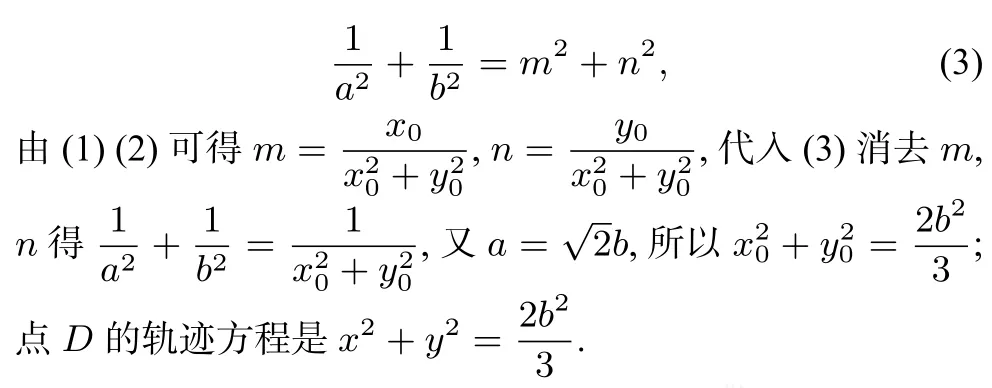
例3 (2009山东高考理科数学22题)设椭圆E:1(a＞b＞0)过两点,O为坐标原点.

图1

(1)求椭圆E的方程;

(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒存在两个交点A,B且OA⊥OB?若存在,写出该圆的方程;若不存在,说明理由.

解(1)椭圆E的方程是

评注本题第(2)问是一个存在性问题,本解法把求圆心在原点的圆是否存在的问题,转化为求切点的轨迹问题,简化了运算.

例4 (2010年高考陕西理科数学改编)如图2,已知椭圆的方程为设n为过原点的直线,l是与n垂直相交于点P,与椭圆相交于A,B两点的直线,|OP|=1,是否存在上述直线l使成立?若存在,求出直线的方程,若不存在说明理由.

图2

(1)求双曲线C的方程;(2)设直线l是圆O:x2+y2=2上动点P(x0,y0)(x0y0/=0)处的切线,l与双曲线C交于不同的两点,请证明∠AOB的大小为定值.

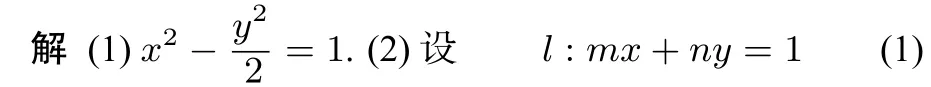
又直线l是圆O上动点P(x0,y0)处的切线,故

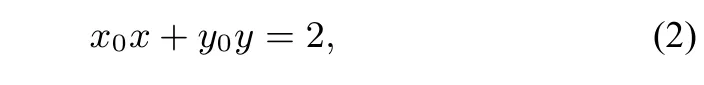
由(1)(2)得x0=2m,y0=2n,P(x0,y0)在O:x2+y2=2上,所以(2m)2+(2n)2=2,即满足根据结论2,则OA⊥OB,∠AOB=90°.

例6 (2008年全国高中数学联赛江苏赛区初试)设A,B为双曲线上的两个动点,满足OA⊥OB,求证:为定值.

图3

解如图3,设直线AB的方程为mx+ny=1,因为OA⊥OB,根据结论2,即