高视点下的高考数学最值问题

广东省始兴县始兴中学(512500)廖春龙 黄奇英

最值问题存在于高中数学的函数、数列、三角、平面向量、不等式、立体几何、解析几何和极坐标与参数方程等各章节的学习过程中,是高中数学的重要题型之一,也是历年高考的热点和学生学习过程中的难点.以求解或讨论最值为载体所设计的问题,不仅可以考查核心概念与重要知识,还能考查函数与方程、分类与整合、转化与化归、数形结合、运动变化等数学核心思想方法.本文在高视点下,对高考中经常出现的最值问题进行分析、讨论,获得求解方法,并且对不同的求解方法加以举例分析,给研究者以最直观的理解.

一、高考数学(理科)中的最值问题

表1:高考数学(理科)中的最值问题

由表1可知,历年高考试题中直接出现“最值”字样的题目均有不少,占分比重大,是高考的高频考点.最值问题载体丰富,求解方法多样.高视点下的高考数学最值问题,定能分析的更为透切.

二、最值问题的求解方法

(一)二次函数法

例题1 (2016年全国I卷第15题)设等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2···an的最大值为____.

关键式为一元二次式,选用一元二次函数法(配方法)求最值.

(二)均值不等式法

例题2 (2017年全国I卷第10题)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )

A.16 B.14 C.12 D.10

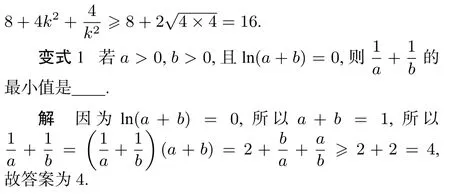
关键式为“类倒数关系”,选用均值不等式法求最值.一元式、二元式均可直接选用.

(三)三角函数法

例题3 (2017年全国I卷第22题)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).

(1)若a=-1,求C与l的交点坐标;

(2)若C上的点到l的距离的最大值为求a.

解(1)略.(2)直线l的普通方程为x+4y-a-4=0,故C上的点(3cosθ,sinθ)到l的距离为

常利用换元方法转化为三角函数求最值,由y=Asin(ωx+φ)+b求最值,有时得把三角转化为二次函数求最值.

(四)导数法

例题4 (2017年全国I卷第16题)如图1所示,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值___.

图1

变式3 (2014年安徽理科第21题)设函数f(x)=1+(1+a)x-x2-x3,其中a＞0.

(I)讨论f(x)在其定义域上的单调性;

(II)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值.

解(I)f(x)的定义域为(-∞,+∞),f′(x)=1+a-2x-3x2,令f′(x)=0,得所以f′(x)=-3(x-x1)(x-x2),当x＜x1或x＞x2时,f′(x)＜0;当x1＜x＜x2时,f′(x)＞0.故f(x)在(-∞,x1)和(x2,+∞)单调递减,在(x1,x2)单调递增.

(II)因为a＞0,所以x1＜0,x2＞0.①当a≥4时,x2≥1,由(I)知f(x)在[0,1]单调递增,所以f(x)在x=0和x=1处分别取得最小值和最大值.②当0＜a＜4时,x2＜1,由(I)知f(x)在[0,x2]上递增,在[x2,1]上递减,所以处取得最大值.又f(0)=1,f(1)=a,所以当0＜a＜1时,f(x)在x=1处取得最小值;当a=1时,f(x)在x=0和x=1处同时取得最小值;当1＜a＜4时,f(x)在x=0处取得最小值.

关键式不适应其他最值方法时,可用导数法求最值.全国高考第21题(函数与导数),常用导数法判断单调性,进而求最值.

(五)数形结合法

例题4 (2017年全国I卷第5题改编)函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的最小值是( )

A.-2 B.-1 C.0 D.1

解模拟一个符合条件的奇函数图像,观察易知|x-2|≤1,所以x最小值为1.选D.

变式4 求函数的值域.

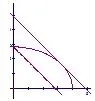
图2

利用数形结合法求最值,具体直观.

(六)线性规划法

例题6 (2017年全国II卷第5题)设x,y满足约束条件则z=2x+y的最小值是( ).

A.-15 B.-9 C.1 D.9

答案:A.

变式5 (2016年全国I卷第16题)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、B产品的利润之和的最大值为____元.

答案:216000.

在二元式中直接求最值(最优解),常用线性规划法.全国高考卷中,近几年都考了此类题目.

三、解最值问题的思维导图

图3

二元式最值问题,先考虑均值不等式,关注线性规划模型,发现数形结合法.能转化为一元式的最值问题,由关键式结构选择二次函数法、均值不等式法、三角函数法等,解决不了的可启用导数法,适时注意观察法、数形结合法.全国高考第21题(函数与导数),一般选用导数法来求最值.

四、最值问题的教学思考

最值问题知识载体丰富,求解方法多样.如果课堂教学中每次都是蜻蜓点水,则学而不会;如果没有全方位的综合比较,则会而不全;如果不提炼各类知识的常规解法,则掌握不牢.一轮教学过程中,多注重“展”,一题多解,一题多变.二轮复习中,常注意“收”,多法寻根,多题归一.

在教学过程中,教师不仅要重视知识传授,更要重视数学思想方法的传递,为学生创设情境体验,一题多解(变),深刻感悟.高视点下的高考数学最值问题,各类解法更清晰明了,数学思想方法更灵活多变.在高视点下解决高考中的最值问题,既能突破此类问题,又能高效培养数学核心素养.