从一道高考题谈异面直线所成角的求法

甘肃省天水市田家炳中学(741000)吴天德

异面直线所成的角是立体几何学习中的第一个空间角,它是后面学习其它空间角的基础,也是近年来高考的热点,它的求法体现了立体几何将空间图形问题化归为平面图形问题的基本思想,但是如何寻找异面直线所成角的平面角将是困扰学生的难点,笔者通过2017年全国卷2高考数学理科选择第10题的多种解法来体会突破这一难点的思想方法,理会求异面直线所成角的解法,以供参考.

真题(2017年全国卷2高考数学理科选择题第10题)已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )

解法1 (抓住异面直线上特殊位置的点(中点)平移)

考察异面直线上的已知点不奏效时,取异面直线上的特殊位置的点是一条有效途径.

解如图1,因为在直三棱柱A1B1C1-ABC中,四边形BCC1B1是平行四边形,连接B1C交BC1于E点,则E是B1C、BC的中点,记AC的中点为F.则EF是△ACB1的中位线,所以EF//AB1,所以∠BEF或它的补角就是异面直线AB1与BC1所成的角.在△ABC中,AB=2,BC=1,∠ABC=120°,由余弦定理知:

图1

解法2 (抓住几何体上的特殊点平移)当异面直线依附在几何体中利用异面直线上的点平移直线有困难时,利用几何体中的特殊点(中点)平移是构造异面直线所成角的一种有效方法.

图2

解法3 (借助异面直线(线段)上的端点平移)过异面直线(线段)上的端点,做另一条直线的平行线,往往是探究异面直线所成角优先考虑的一种方法.

解如图3,过直线AB1的端点B1作B1E//BC1交CB的延长线于E点,连接AE,则∠AB1E或补角就是异面直线AB1与BC1所成的角.因为B1C1//EB,所以四边形B1C1BE是平行四边形,所以

图3

在△ABE中,∠ABE=60°,由余弦定理得:

AE2=AB2+BE2-2AB×BE×cos∠ABE=3,在△AB1E中,由余弦定理得:

所以异面直线AB1与BC1所成角的余弦值是

解法4(借助异面直线(线段)的端点平移)

解如图4,过异面直线BC1的端点B点作AB1的平行线交AB1延长线于E点,由于BE//AB1,B1E//AB,所以四边形ABEB1是平行四边形,则∠C1BE或它的补角就是异面直线AB1与BC1所成的角.

图4

C1E2=B1E2+B1C21-2×B1E×B1C1×cos∠C1B1E=3,在△C1BE中,由余弦定理得:

又异面直线所成角为(0°,90°],所以异面直线AB1与BC1所成角的余弦值是

解法5 (补形平移)“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,以利于直线的平移.利用“补形法”找两异面直线所成的角也是常用的方法之一.

解如图5所示,将三棱柱ABC-A1B1C1补成四棱柱ABCD-A1B1C1D1.因为B1C1//AD,B1C1=AD,所以四边形AB1C1D是平行四边形,所以AB1//DC1,所以∠BC1D或它的补角是异面直线AB1与BC1所成的角.

图5

解法6 (补形平移)把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

解如图6,以△ABC为上底补接一个同样大小的三棱柱ABC-DEF,则∠C1BD或其补角就是异面直线AB1与BC1所成的角,连结DC1,则△C1DB为中,由余弦定理知,

图6

解法7 (基底向量法)选取一组基底,将异面直线所成的角转化为用基底表示的向量的夹角或补角的向量运算,避免找平面角的麻烦.

图7

解法8 (向量坐标法)借助空间直角坐标系,将异面直线所成的角转化为异面直线方向向量夹角的坐标运算.

解如图8,以B为原点,BC所在直线为x轴,过B作BC的垂线为y轴,BB1所在直线为z轴建立空间直角坐标系B-xyz,由于∠ABy=30°,BC=1,AB=2,BB1=1,则:设异面直线AB1与BC1所成的角为θ,则

图8

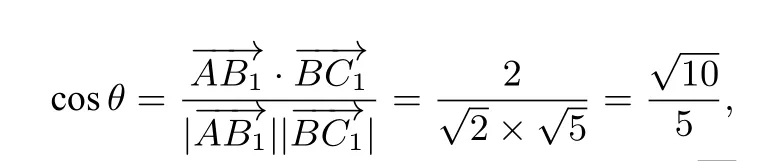
所以异面直线AB1与BC1所成角的余弦值是

通过上面这一道高考题的解法从中体会到要掌握好异面直线所成角的求法,应认真理解和把握以下几点:

1.正确理解概念(1)在异面直线所成角的定义中,空间中的点O是任意选取的,异面直线a和b所成角的大小,与点O的位置无关,因此选取合适的点是异面直线平移的关键.(2)异面直线所成角的取值范围是(0°,90°].

2.熟练掌握求法明确求异面直线所成角的思路:将空间角如何转化为平面角,通过2017年全国卷2选择题第10题的探究发现,解法的空间之大,而突破这一难点的关键:一是思想:如何将空间角转化为平面角,这也是解题的的指导思想.二是方法:(1)平移法,通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几何知识求解,整个求解过程可概括为:一找二证三解.而平移的关键是借助关键点,一般是中点,等分点,端点.(2)“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一.(3)利用向量,设而不找,避开寻找平面角的困难,将异面直线所成角的计算转化为代数运算,降低思维难度.

因此,有了思想的引领和方法的应用,求异面直线所成角的瓶颈将会多方破解,有效的提升了不同层次学生的思维的发展,优化了解题路径.