零知识证明应用到区块链中的技术挑战
李康,孙毅,张珺,李军,周继华,李忠诚
1. 中国科学院计算技术研究所,北京 100190;2. 中国科学院大学,北京 100049;3. 内蒙古大学,内蒙古自治区 呼和浩特 010021;4. 布比(北京)网络技术有限公司,北京 100190;5. 重庆金美通信有限责任公司,重庆 400030
1 引言
区块链的出现首次从技术上解决了基于信任的中心化模型带来的安全问题,它基于密码学算法保证了价值的安全转移,基于散列链及时间戳机制保证了数据的可追溯、不可篡改特性,基于共识算法保证了节点间区块数据的一致性。区块链这种技术体系正在深刻地变革着各行各业的生产方式,成为未来数字经济时代价值互联网的构建基石。
自2008年比特币提出以来,区块链技术得到了快速发展和应用,承载着各种功能的区块链平台应运而生,如智能合约平台以太坊、去中心存储平台Filecoin以及金融商业级解决方案Corda等。基于区块链的行业应用也越来越丰富,例如,伦敦证券交易所、伦敦清算所、法国兴业银行、瑞士瑞银集团以及欧洲清算中心等机构联合成立的区块链集团将区块链技术应用到证券领域,旨在通过区块链技术改变证券交易的清算和结算方式;美国Factom公司将区块链技术应用到数字存证领域,尝试通过区块链技术革新商业社会以及政府部门的数据管理和数据记录方式;美国Chronicled公司将区块链技术应用到供应链溯源领域,保证商品的真实性,保护消费者权益。
然而,区块链的公开透明也给用户的隐私保护带来了巨大的挑战。区块链参与方维护一个共同的账本,皆可查看并且验证其他参与方的交易数据,这就给参与方的隐私泄露开了一道大门,如图1所示[1]。因此,隐私保护成为了制约区块链应用发展的瓶颈之一。
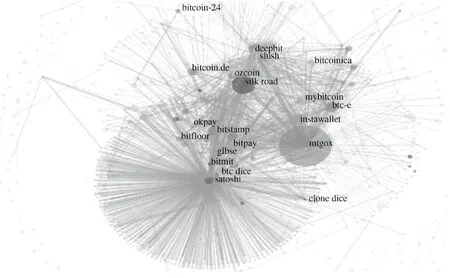
图1 2013年比特币交易图谱
为此,如何在不牺牲区块链人人可验证、公开透明等特性的前提下,使参与方的隐私数据受到保护,成为当前区块链研究领域的主要科学问题。
针对上述现状,本文将总结区块链领域中现有的隐私保护方案,重点围绕零知识证明技术,阐述其如何应用到区块链中实现交易隐私保护,并介绍零知识证明与区块链结合中亟待解决的几个技术挑战。
2 区块链隐私保护方案研究现状
区块链中最主要的组成部分就是交易,交易是驱动区块链系统运转的信息载体,通过交易,区块链节点可以将资金在用户之间进行转移,并进行一系列更为复杂的操作,比如执行相关的智能合约。交易涉及的基本元素有发送方、接收方、金额,虽然发送方与接收方在区块链系统中一般表示为公钥地址,但是辅之社会学挖掘方法,可以将现实世界中的真实身份与公钥地址联系起来,而区块链作为公开的交易账本,任何人均可从中查出其他用户在该系统中发生过的行为,如资金流转过程、合约执行过程等,从而泄露了用户的隐私。因此,如何保证用户在区块链系统中的操作行为不被其他人获取是区块链隐私保护的主要内容,而实现这一目标的解决方案就是保护交易的关键性信息不被泄露。
自比特币后的区块链平台纷纷开始重视交易的隐私保护,并从协议级别支持交易的隐私保护,而且无需丧失区块链公开可验证的特性,这为区块链的进一步应用发展奠定了基础。
达世币①https://github.com/dashpay/d a s h/w i k i/Whitepaper是最早在区块链中实现了交易隐私保护并且得到大规模应用的平台。它采用了一种称为混币的技术,实现了匿名发送(darksend)的功能。匿名发送是混币技术的一种实现版本,基本思想是使用网络中的主节点将来自多个用户的交易混合形成单笔交易。在达世币匿名发送中,每个用户需将交易发送至主节点,主节点需要至少3笔交易进行混合,然后形成单一交易中的多个输出,同时确保输出乱序。为了从整体上提高系统隐私性,规定使用固定面值0.1、1、10、100的交易金额,在每轮混币过程中,所有用户应该提交相同面值的输入与输出,除了使用相同面值外,交易手续费会从交易中移除,并且在独立、不可链接的交易中支付。在匿名发送中,主节点承担了保护隐私的责任,存在被攻击的可能。通过引入链式混合(chaining)技术,用户会随机选择多个主节点,这些主节点构成一条链,最后输出混合后的交易;通过引入基于中继系统的盲化技术(blinding),用户可不直接向交易池提交交易,相反在全网中随机选择主节点,然后要求该主节点将交易提交至目标主节点,这样目标主节点就难以获取用户的真实身份。但是达世币的局限性在于,节点始终需要信任网络挑选的主节点以及参与混币服务的用户,一旦主节点被控制,或者参与混币的用户是恶意的,都会在一定程度上导致用户隐私泄露。
为了避免达世币中存在的主节点信任风险,门罗币②https://getmonero.org/采用了一种不依赖于主节点的加密混合方案,其中涉及两个关键的技术点:一是隐秘地址技术,另一个是环签名技术。隐秘地址的基本原理是,当发送者发送一笔资金时,首先通过接收者地址,基于椭圆曲线生成一次性公钥,然后发送者将交易连同附加信息广播到区块链网络中,接收者时刻使用自己的私钥监测区块链中的交易,如果能成功解析该交易,证明发送者已发送相关交易;当接收者想要花费交易时,使用私钥连同附加信息计算出签名私钥,对交易进行签名即可花费,保障了输入与输出地址不可关联的特性。环签名基本思想是利用自己的私钥以及若干个用户的公钥对交易签名,验证签名时,则使用其他人的公钥以及签名中包含的参数,从而达成隐藏发送者信息的目的。但是门罗币的局限性在于,用户在使用环签名技术时,需要依赖其他用户的公钥,如果其他用户是恶意的,则会在一定程度上导致用户隐私泄露。
2016年11月,国际著名银行区块链联盟R3组织开源了其为金融机构打造的商业级解决方案——Corda平台③https://docs.corda.net/_static/corda-technicalwhitepaper.pdf。在金融机构业务环境中,隐私保护是必不可少的一环,Corda在这方面下了不少工夫。首先,传统的区块链中,所有节点都会维护一个共同的账本,隐私泄露的可能性会大大增加,因此,Corda直接摒弃了交易进行广播的行为,只在交易相关方之间进行交易的传播与见证。其次,采取了敏感信息抽离(tear-off)技术,即将敏感信息进行散列,并且组成分层 Merkle树,使得非敏感信息仍可以通过 Merkle树进行分支验证,而一旦出现法律纠纷时,可以申请披露敏感信息,进行验证。最后,采用了复合签名技术,通过为每个签名主体赋予协商好的权重,辅以签名阈值设置,则可以设置灵活的签名方案,从而保护签名人的信息。
2016 年 11 月,以隐私为主要功能的零币(Zcash)[2]区块链系统进行了开源,致力于打造一个完美的隐私保护平台。零币使用了零知识证明中最为著名的zkSNARKs[3-10]技术,该技术具有非交互性、简洁性、公开可验证等特性。零币系统中有透明地址与匿名地址之分,使用匿名地址可达到交易隐私保护的目的,包含匿名地址的交易称为隐秘交易,隐秘交易将发送方、接收方、转移金额全部隐藏在生成的零知识证据中,区块链节点根据事先生成的零知识证据验证密钥,可验证隐秘交易的真实性,保证只有真实的发送方在有真实资产的情况下才可以完成一笔有效的隐秘交易。由于隐秘交易不包含发送方、接收方、转移金额等关键性信息,使得攻击者无法根据交易追溯性获取更多信息,从而有效地保护了用户的隐私。
除上述已应用到区块链平台进行隐私保护的技术之外,区块链研究人员还将同态加密技术④https://en.wikipedia.org/wiki/Homomorphic_encryption列为隐私保护的关键性密码学技术。同态加密的特性使得交易相关方见证明文,而交易无关方可以见证密文,即可验证交易的有效性。但是由于同态加密技术效率较为低下,与区块链的结合还处于一个相对初级的阶段。如果未来同态加密技术取得重大突破,将会大大促进同态加密技术在区块链系统中的应用。
3 零知识证明应用到区块链中的技术挑战
零知识证明是指一方(证明者)向另一方(验证者)证明一个陈述是正确的,而无需透露除该陈述正确以外的任何信息,适用于解决任何NP问题。而区块链恰好可以抽象成多方验证交易是否有效(NP问题)的平台,因此,两者是天然相适应的。将零知识证明应用到区块链中需要考虑的技术挑战分为两大类:一类是适用于隐私保护的区块链架构设计方案,包括隐秘交易所花资产存在性证明、匿名资产双花问题、匿名资产花费与转移、隐秘交易不可区分等技术挑战;另一类是零知识证明技术本身带来的挑战,包括参数初始化阶段、算法性能以及安全问题等技术挑战。
3.1 隐秘交易所花资产存在性证明
在不使用零知识证明的区块链系统中,证明交易所花资产存在有两种模型:未花费的交易输出(unspent transaction outputs,UTXO)模型与账户模型。在UTXO模型中,每一笔交易的输入会引用来自前一笔交易的输出,区块链节点会根据保存的UTXO集合来验证一笔交易花费资产是否存在;在账户模型中,每一笔交易会指定发送方,区块链节点会根据保存的账户信息验证一笔交易花费资产是否存在并且足够。如果在区块链中使用零知识证明保证交易的隐私,首要解决的就是如何证明隐秘交易所花资产存在于区块链上。由于隐秘交易隐藏了发送者地址信息,所以隐秘交易所花资产不能来源于区块链中已存在的透明资产,也就意味着不能明确地引用前一笔交易输出或者账户。因此,隐秘交易花费的资产应该是匿名的,这就需要设计一套机制来发行匿名资产,并对匿名资产进行标识。零币系统中存在两种匿名资产发行机制:一是花费“挖矿”所得的奖励,即将奖励转换为匿名资产,这样做的目的是为了系统中有足够多的匿名资产,防止匿名资产被追踪;二是通过正常的交易将透明资产转换为匿名资产。那么,当隐秘交易花费匿名资产时,如何让区块链节点相信该匿名资产的存在?零币系统给铸造的每一个匿名资产打上一个数字承诺的烙印,并将这些数字承诺组织成一棵Merkle树,用来标识系统中已出现过的所有匿名资产(包括花费和未花费的)。隐秘交易包含匿名资产所在的Merkle树的根散列值以及证明该匿名资产确实存在于Merkle树中的零知识证据,区块链节点通过公开的验证密钥可验证隐秘交易所花费的资产确实在区块链的系统中出现过,但是不知道具体是哪一个匿名资产,也不能证明该匿名资产是否已经被花费,因此会存在双花问题,接下来将会探讨如何解决匿名资产双花的问题。综上所述,区块链交易隐私保护方案需要设计一套匿名资产发行机制及存在性证明机制(Merkle树),确保其公开可验证特性。
3.2 匿名资产双花问题
区块链要解决的一个最核心的问题就是资金双花,在UTXO模型的区块链中,区块链节点都要维护UTXO集合,当验证一笔交易时,将该交易引用的输出从UTXO集合中移除,这样当验证另一笔花费同样输出的交易时,会因为在UTXO集合中无法查找到该输出而变得无效。在账户模型中,区块链节点皆维护账户状态,其中包括余额,当验证交易时,首先会判断账户余额是否足够,因此也可有效阻止双花。为了实现区块链交易隐私保护,需要使用匿名资产,然而会存在双花问题,所以需进一步加强匿名资产在区块链中的属性。零币系统赋予每一个匿名资产唯一的序列号,区块链节点将出现过的所有序列号保存起来,当发起一笔隐秘交易时,需要披露序列号,节点检查该序列号是否已经出现过,这样能够有效地阻止匿名资产的双花问题。注意,应选择合适的散列函数以及随机数,编码匿名资产数字承诺与序列号,确保它们相互关联,并且一一对应。
3.3 匿名资产花费与转移
在不使用零知识证明的区块链系统中,资产花费是通过公钥私钥对进行的,资产转移是通过在交易中指定接收方地址完成的。为了实现隐私保护,隐秘交易需要隐藏发送者以及接收者,那么区块链节点如何验证匿名资产被拥有的人花费,并且转移到了合适的接收方?隐秘交易花费的是匿名资产,匿名资产应至少包括金额、所属公钥地址等属性,因此,在生成匿名资产时,需要将金额、所属公钥地址编码进数字承诺。当花费一笔匿名资产时,将私钥、公钥与数字承诺之间的生成关系编码进零知识证据中,结合匿名资产存在性证明,区块链节点可使用零知识证明的公开验证密钥来验证数字承诺确实存在,而且是通过相应的公钥地址、金额生成,并且发送交易的人拥有公钥地址对应的私钥,确保只有匿名资产所属者才拥有花费的权利。
匿名资产所有权的转移是如何发生的?由于隐秘交易中不含接收方,并且每一个匿名资产都与所属者公钥相关联,因此采用销毁旧匿名资产、生成新匿名资产的策略保证匿名资产的转移。匿名资产数字承诺的生成需要所属公钥地址、金额等信息,并且这些原始信息也要发送给接收方,因此接收方需要提供两个公钥,一个是支付公钥,一个是加密公钥。支付公钥供发送者生成数字承诺,加密公钥供发送者加密生成数字承诺过程中用到的信息。当然,支付公钥与加密公钥可以是同一个,但是为了安全着想,建议使用不同的公钥。接收方需要监听区块链上的交易,尝试用自己的私钥解密隐秘交易中包含的加密信息,如果解密成功,则代表该隐秘交易的接收方是自己,将该匿名资产归入自己的支付密钥对账户下,便于以后花费。
除匿名资产花费以及转移外,还应将花费的资产总额与转移产生的资产总额之间的关系编码进零知识证据,即花费的资产总额应该大于或等于转移产生的资产总额,以保证隐秘交易的有效性。
综上所述,零知识证明应用到区块链中需要设计一套合理的匿名资产所有权验证规则及转移规则,将这些规则使用零知识证明技术编码进零知识证据,从而达到区块链公开可验证的特性。
3.4 隐秘交易不可区分特性
为达到交易隐私保护的目的,区块链中的隐秘交易理应是不可区分的,即无法通过对比、分析隐秘交易对其进行聚类。另外,由于零知识证明需要电路(验证规则转换而来)是固定的,因此,在使用零知识证明的区块链中,隐秘交易应该具有固定的输入与输出数量,当输入与输出数量无法满足规定数量时,应该构建随机冗余的输入与输出,并且生成的零知识证据中应包含判定输入与输出是冗余还是真实的条件,区块链节点接收到隐秘交易时,会根据输入与输出的真实与否决定是否处理对应的匿名资产,隐秘交易的不可区分特性进一步加强了交易隐私的保护。
3.5 零知识证明初始化阶段
零知识证明分交互式与非交互式两种,而在区块链的系统中,交互式是不适合的,因为区块链中的每一个节点都要验证交易的有效性,而交互式需要发送方与区块链系统全网验证节点进行信息交换才能达到保护隐私的目的,所以在区块链系统中应该采取非交互式零知识证明。非交互式零知识证明中,z k SNAR K s最为成熟。z k SNAR K s算法需要一个中心化的初始化阶段,用于创建生成零知识证据的证明密钥以及验证零知识证据的验证密钥。而区块链本身是一个去中心化的系统,那么zk SNARK s算法的初始化阶段无疑给区块链带来了信任风险,因此如何保证zkSNARKs算法可信地构造初始化阶段是应用到区块链中需要克服的关键性技术挑战。零币系统中设计了一种多方安全计算式的初始化阶段[11],即多方在不泄露各自信息的前提下协同计算出证明密钥与验证密钥,但是证明密钥与验证密钥只需生成一次,后续可以反复使用。但是零币系统使用的多方安全计算局限于少数人,无法让更多人参与进来,因此后续需要进一步改进多方安全计算的性能,使zkSNARKs算法初始化的构建方案更加去中心化。
3.6 zkSNARKs算法性能
zkSNARKs算法目前的性能较差,计算复杂度主要来自于底层依赖的椭圆曲线配对运算,目前零币系统使用的是BN254椭圆曲线[12],生成一笔隐秘交易对应的零知识证据需要40 s左右,并占用约4 GB内存⑤https://z.cash/blog/cultivatingsapling-fasterzksnarks.html,这导致无法在现有的移动设备上使用 zkSNARKs算法,并且40 s的时间在高并发场景下也显得很慢。因此需要精心设计对配对操作友好的椭圆曲线,目前已有相关研究进展,例如零币系统开发者已设计出BLS12-381[13]椭圆曲线,初步测试,可以将生成零知识证据的时间缩短到7 s,内存占用缩减到40 MB左右,大大提高了zkSNARKs算法的可用性。
zkSNARKs算法安全性依赖于底层选取的椭圆曲线,BN254椭圆曲线实现的安全性约为128 bit,最近有研究[14]表明,BN类椭圆曲线的安全性实际为 110 bit左右。因此设计椭圆曲线时,应考虑该曲线对应的安全性。
综上所述,当零知识证明算法应用于区块链隐私保护时,需要满足区块链的核心功能特性,即资产确权及转移和防止双花。本文基于零知识证明算法,给出了一套匿名资产发行、转移机制,在保护用户隐私的同时有效地实现了资产确权和转移以及防止双花的功能特性。在零知识证明与区块链实际结合中,建议使用成熟、高效、安全的zkSNARKs算法,并给出了zkSNARKs算法进一步优化的方向。
4 结束语
在数字经济全球化背景下,区块链技术的出现使得通过互联网进行价值转移成为可能,然而区块链的公开透明特性也给人们的隐私保护带来了巨大的挑战,因此如何实现隐私保护成为了阻碍区块链进一步发展的难题。
本文详细讲解了当下区块链平台实现隐私保护采取的方法,重点围绕零知识证明技术展开,阐述了零知识证明与区块链结合需要考虑的几个常见问题,并且对零知识证明在区块链中的技术挑战做了说明。未来区块链的隐私保护仍然任重而道远,如何实现快速高效、可信的零知识证明算法以及如何实现能够抵抗量子计算的零知识证明算法,都是需要进一步解决的问题。
[1] M E I K L E J O H N S, P O M A R O L E M,JORDAN G, et al. A fistful of bitcoins:characterizing payments among men with no names[C]//The 2013 Conference on Internet Measurement Conference,O c to b e r 23-25, 2013, B arce l o na,Spain. New York: ACM Press, 2013:127-140.
[2] SASSON E B, CHIESA A, GARMAN C,et al. Zerocash: decentralized anonymous payments from Bitcoin[C]//The 2014 IEEE Symposium on Securit y and Privacy, May 18-21, 2014, San Jose,USA. Washington, DC: IEEE Computer Society, 2014: 459-474.
[3] J E N S G. S h o r t p a i r i n g-b a s e d non-interac tive zero-k nowle dge arguments[C]//The 16th International Conference on the Theory and Application of Cryptology and Information Security,D e ce m b e r 5-9, 2010, Si n g a p o r e.Heidelberg: Springer, 2010: 321-340.
[4] LIPMAA H. Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments[C]//The 9th International Conference on Theory of Cryptography, March 18-21, 2012, Sicily,Italy. Heidelberg: Springer-Verlag, 2012:169-189.
[5] N I R B, A L E S S A N D R O C, Y U VA L I.Succinct non-interactive arguments via linear interactive proofs[C]// The 10th Theory of Cryptography Conference on Theory of Cryptography, March 3-6, 2013,Tokyo, Japan. Heidelberg: Springer-Verlag, 2013: 315-333.
[6] GENNARO R, GENTRY C, PARNO B, et al.Quadratic span programs and succinct NIZKs without PCPs [C]//The 32nd Annual International Conference on the Theory & Applications of Cryptographic Techniques, May 26-30, 2013, Athens,Greece. [S.l.:s.n.], 2013: 626-645.
[7] PA R N O B, H O W E L L J, G E N T R Y C,et al. Pinocchio: nearly prac tical verifiable computation[C]//The 2013 IEEE Symposium on Security & Privacy,May 19-22, 2013, San Francisco, USA.Washington, DC: IEEE Computer Society,2013: 103-112.
[8] BEN-SASSON E, CHIESA A, GENKIN D,et al. Verifying program executions succinctly and in zero knowledge[C]//The 33rd International Cryptology Conference(CRYPTO 2013), August 18-22,2013, Santa Barbara, USA. Heidelberg:Springer-Verlag, 2013: 90-108.
[9] LIPMAA H. Succinct non-interactive zero knowledge arguments from span programs and linear eror-correcting codes[C]//The 19th International Conference on Advances in Cryptology,December 1-5, 2013, Bangalore, India.New York: Springer-Verlag New York,Inc., 2013: 41-60.
[10] BEN-SASSON E, CHIESA A, TROMER E,e t a l. S u c c i n c t n o n-i n t e r a c t i v e zero knowledge for a von neumann architecture[C]//The 23rd USENIX Conference on Security Symposium,August 20-22, 2014, San Diego, USA.Berkeley: USENIX Association, 2014:781-796.
[11] BEN-SASSON E, CHIESA A, GREEN M,et al. Se cure s ampling of public parameters for succinct zero knowledge proofs[C]// 2015 IEEE Symposium on Security and Privacy (SP), May 18-21,2015, San Jose, USA. Piscataway: IEEE Press, 2015: 287-304.
[12] PEREIRA G C C F, JR M A S, NAEHRIG M,et al. A family of implementationfriendly BN elliptic curves[J]. Journal of Systems and Software, 2011, 84(8):1319-1326.
[13] ARANHA D F, FUENTES-CASTAÑEDA L,KNAPP E, et al. Implementing pairings at the 192-bit security level[C]//The 5th International Conference on Pairing-Based Cryptography, May 16-18, 2012,Cologne, Germany. Heidelberg: Springer-Verlag, 2012: 177-195.
[14] M EN E ZE S A, SAR K AR P, SIN G H S.Challenges with assessing the impact of nfs advances on the security of pairing-based cryptography[C]// International Conference on Cryptology, December 1-2, 2016, Kuala Lumpur, Malaysia. Heidelberg: Springer-Verlag, 2016: 83-108.

